Hao Wang's Life and Achievements*

Shangshui Zhang，Jialong Zhang，Qingyu Zhang†

Institute of Philosophy，Chinese Academy of Social Sciences

zhangjialong@hotmail.com

Lu Wang

Philosophy Department，Tsinghua University

wlwl@tsinghua.edu.cn



Hao Wang's Life and Achievements*

Shangshui Zhang，Jialong Zhang，Qingyu Zhang†

Institute of Philosophy，Chinese Academy of Social Sciences

zhangjialong@hotmail.com

Lu Wang

Philosophy Department，Tsinghua University

wlwl@tsinghua.edu.cn

Abstract.Hao Wang（1921-1995）is an internationally renowned Chinese-American mathematical logician，computer scientist and philosopher.This paper is divided into three parts：（1）Introducing his life and major works；（2）Discussing his pioneering contributions in the fields of mathematical logic and computer science，including following five aspects：set theory，∀∃∀and domino theory，Wang machines，computer proof of theorems and logical semantics；（3）Reviewing his contribution to the philosophy.

As a well known logician，computer scientist and philosopher，Hao Wang is successive and fruitful in his academic career and has made great contributions to logic，computer science and philosophy，It is quite difficult to make an appropriate evaluation on his work，which ranges far and wide，and of great quantity.So in this paper we are going to deal with only three aspects：

1.His life and works，

2.His contributions to logic and computer science，and

3.His contributions to philosophy.

1　His Life and Works1In this part we have consulted mainly the papers by Professor Yunzeng Wu：Conversations with Hao Wang concerning his Intellectual Development，in A Collection of Yunzeng Wu's Works，Beijing Science and Technology Press 1991，pp.257-264；Hao Wang's Contributions to Logic，in A Collection of Yunzeng Wu's Works，Beijing Science and Technology Press 1991，pp.265-272）.

Hao Wang was born in an intellectual family in Shandong Province of China in 1921.His father was the director of a middle school in Jinan，the Capital of Shandong Province，studying in a middle school in Changsha of Hunan Province at the age of 17，hebeganthinkingabouthislifeandfuture，thatis，tochoosebetweentwopossible ways：eithertodosomepracticalthingsortounderstandtheworld.Justatthattimehe accidentally got a logical book that had been newly published by the famous Chineselogician Yuelin Jin.Deeply attracted by that book，he began having great interest in mathematical logic.

In 1939，Hao Wang went to the South-West United Universities（an university established in Kunming during the Second World War through the combinations of Peking University，Tsinghua University and Nankai University）with mathematics as his main subject.In the first year of his study in the university，he studied mathematical logic as a selected course，which was given by Professor Xianjun Wang for the students of senior grades.During the period from 1939 to 1940，he spent a great deal of time studying the Principia Mathematica by Whitehead and Russell.And in order to read the original works of German logicians，he began in the second year of the university studying German and reading the Grundlagen der Mathematik by Hilbert and Bernays.

Having graduated from the department of mathematics in 1943，Hao Wang was enrolled as a post graduate student by the department of philosophy of Tsinghua University.In the coming two years he published in Chinese two papers：one was“The Metaphysical System of the New Li-Hsuen”（in Philosophical Review of the Chinese Philosophical Society，1944，vol.10，pp.39-62），and the other“Language and Metaphysics”（ibid.，1945，vol.10，pp.35-48），and in 1945 he finished his essays for M. A.entitled“Essays on the Foundation of Empirical Knowledge”.

In 1946 Hao Wang won a scholarship through fierce competition and went to the United States for advanced studies.First he studied in Brown University，and then he went to study in the Harvard University.During this period he began studying Quine's system of ML.As a result he put forward a plan for revising Quine's system，with which the“paradox”discovered recently in the original system was avoided and all the results of Quine's work still could be deduced，and which was appreciated much by Quine.In 1947 Hao Wang finished his M.A.essays based on the revision and improvement of Quine's system of mathematical logic.And in June 1948 he got his PhD and began his teaching career in the Harvard University.

In 1949 Hao Wang published the paper“On Zermelo's and von Neumann's Axioms for Set Theory”，which contained the main ideas of a new set theory.And in the same year he put forward for the first time the conception of impossibility of finitization of impredicativity，which was later developed further in the articles of other scholars.

From 1949 to 1950 Hao Wang felt the possibility of proving that mathematical analysis was inconsistent.He wrote an argument for it in detail and sent it to Bernays and Rosser in 1951.At that time Bernays held that this result was probably right because he did not find defects in the argument until several months past.Then Hao Wang revised his work.And the result he got in his paper“Truth Definition and Consistency Proofs”（in Transaction of American Mathematical Society，vol.73，1952，pp.243-275）was based partly on this research.

Under the auspices of Bernays，Hao Wang visited ETH of Zurich from the au-tumn of 1950 through the spring of 1951.And in 1951 he held a series of lectures on set theory in Pairs University and with the cooperation of McNanghton he published a book in French based on the teaching materials for these lectures.

In 1953 he published the paper“Between Number Theory and Set Theory”and stated for the first time the differences between the predicative set theory and impredicative set theory.In the same year he also published the paper“Logic of many-sorted theories”，and“Certain Predicates Defined by Induction Schemata”which was the earliest paper about the concept of inductive definition.And in this year Hao Wang began his research of Σ system.

During this period Hao Wang published a number of philosophical papers as well.After 1953 Hao Wang turned to some basic research concerning the technique of computer.And in July 1953 he entered the Burraughs Company for a one-year research.He put forward a new type of ideal computer，the distinguished character of which was that it had an non-erasable memory system and its power was same with Turing machine.This machine could be taken as a proper model for real machines. Furthermore，it had also the interesting mathematical properties concerning spatial complexities.

In the spring of 1954 Hao Wang accepted the appointment of Oxford University to be the John Locke lecture and went to England in the autumn.First he lived in Cambridge and then he arrived at Oxford，holding the John Locke Chair from February to May 1955.In the autumn of this year he went back to the U.S.A.to deal with some private things.He stayed there for one year and wrote an unfinished work about the principles of mathematical philosophy.In 1956 he went to Oxford again，holding a seminar on Wittgenstein's Bemerkungen（Remarks On the Foundations of Mathematics），which was successful and in which Hao Wang's paradox was put forward.

In the summer vacation of 1957 Hao Wang spent his holidays in the U.S.A.，and first in the IBM Company，then in the Institute of Summer Vacation of Cornell University，andatlastinMichiganUniversity，wherehewrote“LogicofAutomata”in cooperationwithA.Burks.Andhealsowrote“EightyYearsofFoundationalStudies”（in Dialectica，12（1958），pp.466-497）.

In the summer of 1958 Hao Wang spent most of the time of his summer vacation in IBM Company and got many achievements.With the language of SAP of the machineofIBM704hecompiledtheprogrammeofprovingthetheoremsofPrincipia Mathematicaandonthismachineheprovedinlessthannineminutes350theoremsof the first order logic.This caused a sensation in the mathematical field.He reported this special topic after returning to Oxford.In December of this year he wrote his paper“Toward Mechanical Mathematics”and published it in 1960.

From 1957 Hao Wang delivered lectures of the principles of mathematical philosophy，settheory，etc.，andhevisitedRussellonFebruary16，1957，andhadteawith Russell and tried unsuccessfully to explain to Russell the extensions of his ramified type theory.

On Schuett's suggestion Hao Wang began his research of the∀∃∀problem and with help of some students he solved the problem in a negative result in 1961.The method he used was an application of“tiling theory”，which was also called“domino theory”andhadbeendiscoveredbyhiminJanuary1960.Showinghisenthusiasmfor this theory，Edward Moore said that it would be possible to get all the prime numbers by means of the“domino theory”.And later Hao Wang provided the“domino set”that could be used to simulate the Turing machine，thus the“tiling theory”became a powerful instrument useful outside logic and mathematics.Hao Wang's solution of the∀∃∀problem and creation of this theoretical instrument laid a milestone in the history of mathematical logic.

In 1960 Hao Wang was invited by McCarthy to stay as an adviser of the summer vacation in MIT for two months.In June of the same year Hao Wang gave two lectures in Harvard University and soon after that he was invited to return to Harvard University again.

InJuly of 1961，as a professor of mathematical logic，Hao Wangreturned to Harvard University，being invited by the Department of Applied Mathematics.In this year he wrote“Mechanical Mathematics and Inferential Analysis”and also gave lectures about his tiling theory in Harvard University，Besides that he，with help of A.S. Kahr，thenapostgraduatestudent，extendedtheinsolvabilityoftheorigin-constrained dominoproblemtothatofdiagonalconstraineddominoproblem，provingthatthe∀∃∀case was undecidable and that it was a reduction class.And the paper about this result was published in 1962.

In the early sixties Hao Wang wrote a number of papers，some of which showed the examples of supplementing by means of computer the steps omitted and jumped in mathematical proofs.He also gave a very interesting indication that it was possible to simplify by means of computer the complete artificial formal proof.In his paper “Proving Theorems by Pattern Recognition”Hao Wang put forward some very good methods for automatically proving theorems，which would，when put to effective development，probablyleadtogreatleapsinthisfield.AndthescientistsinSovietUnion at that time showed interest for Hao Wang's work about mechanical mathematics.

In 1962 Hao Wang's collected work A Survey of Mathematical Logic（Science Press，Peking）was published and it contained his papers published before 1959 and also some papers specially written for it.

From about 1963 Hao Wang turned his main interest to the problems of conceptions concerning set theory，mechanical process，and，more generally，cognitive philosophy and more extensive problems of philosophy.In 1964 he wrote the paper “Russell and his Logic”（Ratio，vol.7，1965，pp.1-34）.

In 1967 Hao Wang went to work as a professor of mathematical logic in Rockefeller University，leading the work of logic section，where gathered at the end of the sixties and the beginning of seventies a large number of outstanding logicians，including Robert Solovay，D.A.Martin，Saul A.Kripke，etc.

In1967HaoWangfinishedwritinghisfirstdraft“ASurveyofSkolem'sWorkin Logic”andsentittoGödelforcriticismbecauseoftheinvolvementoftherelationship between Gödel's completeness theorem and Skolem's work.And in December 7，1967 and March 7，1968 Gödel wrote him back two letters of great importance.Thus HaoWangbeganhisclosecontactswithGödel.Andhewasoneoftheyoungscholars in the same field with whom Gödel was most close in his later time.From October 1971 through December 1972 Hao Wang visited to Gödel's office for discussions for two or three hours almost every two weeks.In 1975 Gödel invited Hao Wang to visit the Institute for Advanced study for 15 months and they had a series of new discussions again.

During the period from 1967 to 1972 Hao Wang's main achievement was his important book“From Mathematics to Philosophy”，which was finished in June 1967 and published in 1974.

In the summer of 1972 Hao Wang visited China，his native land which he had left for more than 20 years.He showed great concern for and turned his attention to China.

In 1976 Hao Wang published，in cooperation with B.Dunham，the paper“TowardFeasibleSolutionsoftheTautologyProblem”（inAnnalsofMathematicalLogic，vol.10，1976，pp.117-154）.TheyprovedthatforalargeclassofBooleanexpressions therewasadecisionprocedureinpolynomialtime，thiswasanimportantcontribution to the theory of computational complexity.

Intheautumnof1977HaoWangvisitedBeijingbytheinvitationofTheChinese Academy of Sciences，where he made a series of reports about mathematical logic. Having returned to the U.S.A.，he added a great deal of material to his original lecture notes and wrote the book Popular Lectures on Mathematical Logic（Chinese and English versions by the Science Press，Beijing，and Van Nostrand Reinhold，New York，1981）.This book was not very long，but of rich content，ranging over the various branches of mathematical logic and stating briefly the history of mathematical logic and its application in computer，so，that it was not“popular lectures”in the general sense，but a book of special characters.

In1977，HaoWangpublishedthepaper“LargeSets”.Andfrom1977to1984he had published a large number of papers，the contents of which dealt with wide field，including philosophy，mechanical treatment of Chinese characters，and the intuitive in biological sciences，etc.

In1985hepublishedanotherimportantphilosophicalbookBeyondAnalyticphilosophy：Doing Justice to What We Know（Cambridge，MA，MIT Press）.In this year he also published his paper“Two Commandments of Analytic Empiricism”（in The Journal of Philosophy，vol.82，1985，pp.449-462）.And next year he published his paper about Quine：“Quine's Logical Ideas in Historical Perspective”（in The Philosophy of W.V.Quine，pp.623-643）.

In 1987 Hao Wang published his book entitled Reflections on Kurt Gödel（MITPress），which was the first one of his two important books about Gödel and also the firstcriticalbiographyaboutGödelingeneral.Thisbookwasdividedintothreeparts. The first part made an introduction to Gödel's life and deeds，the second part dealt with his thought，and the third part interpreted in detail his articles of mathematics and philosophy.One of the characters of this book was that it placed Gödel in a very important position in the history of mathematical philosophy.In his commentary of this book，Martin Davis wrote：“Hao Wang has provided us with an invaluable source book on one of the most remarkable thinkers of our century.”（in Nature，1988，p. 399）A Logical Journey：From Gödel to Philosophy，Hao Wang's second book about Gödel，which contained the records of the conversations and discussions between Gödel and Hao Wang，had not been published before his death.On May 13，1995，Hao Wang was dead for cancer in New York.

2　Contributions to Logic and Computer Science

2.1Wang's set theory

Hao Wang began to work in the axiomatization of set theory from repairing the system proposed by Quine in 1940 in his book“Mathematical Logic”.In 1950（J. Symbolic Logic，15，pp.25-32），he repaired the system so that the result is an impredicative extension of NF（Quine's New Foundation）.This modified system has been adopted by Quine in the third edition of his book Mathematical Logic and is often known in the literature as ML.His thesis for graduation is composed of the system.

In 1949，Hao Wang published the paper“On Zermelo's and von Neumann's axioms of set theory”（Proceedings of the National Academy of Sciences，U.S.A.35，pp.150-155）.The paper contains the major idea of a new type of set theory，which is known as the Moore-Kelly set theory.

Hao Wang has done many works in predicative set theory.He firstly has made the sharp distinction between predicative and impredicative set theory in his paper “Between Number Theory and Set Theory”（Math.Annal 126，pp.385-409），and hence has open up a new research field-predicative set theory.In 1953，he began to study his system Σ.In 1954，he published an important paper“The formalization of mathematics”（Journal of Symbolic Logic 19，pp.241-266）about Σ.In 1959，he published the paper“Ordinal number and predicative set theory”（Zeitschrift für Mathematische Logik und Grundlagen der Mathematik，5，pp.216-239）which contains some results in this connection.

The presentation of the system Σ aims at preserving the desirable features of a ramified type theory but avoiding its undesirable traits without recourse to such dubious means as an axiom of reducibility.The hierarchy of objects in Σ differs from that of Russell's ramified class-calculus.It is a one-dimensional array.It has in the lowest order（the 0thorder）a denumerable totality（which may be taken to be，forinstance，the positive integers or all the finite sets built up from the empty set）.It has in the first order all the set of the 0thorder plus sets of them which can be defined by formulas that contain no bound variables ranged over sets of the first or higher order. Similarly，for every positive integer n，the sets of order n+1 include all sets of order n together with sets of them defined by formulas whose bound variables range over sets of the nthorder at most.The sets of order ω include all and only sets of the finite order.For any ordinal number α+1，the sets of order α+1 are related to those of order α in the same way as the sets of order n+1 to those of order n.For any ordinal number β which is the limit number of a monotone increasing sequence α1，α2，…of ordinals，the sets of order β are related to the sets of orders α1，α2，…in the same way as the sets of order ω are related to those of finite orders.Hao Wang uses only constructive ordinals.

The primitive symbols which are used to form terms and sentences of the system Σ are the following：

1.Variables—foreachconstructiveordinalnumbersα，xα，yα，zα，uα，wα，…are variables of order α；

2.The sentence connectives¬（not），∨（or）；

3.The abstraction symbolˆ；

4.The membership relation symbol∈；

5.The grouping symbols（，），［，］，｛，｝；

6.The existential quantifiers（∃xα），（∃yα），（∃zα），…for all α and all variables of order α.

The system Σ is based on seven axiom schemata（AxI～AxVII）and eight rules of inference（Ri1～Ri8）.We use the formula p→q to indicate that if p is a theorem then q is also；similarly，p，q→r indicates that if p，q are theorem then r is also.

AxI.The law of excluded middle.For every sentence p of Σ，¬p∨p.

AxII.The axioms for identity：for every γ，γ≥α，γ≥β，

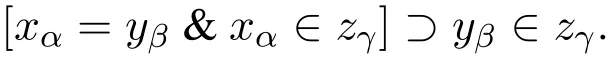
AxIII.The axioms of infinite summation：for every limit number α，if β＜α，then

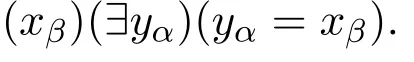
AxIV.The axioms of abstraction：

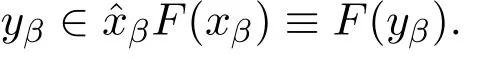
AxV.The axioms of pair sets：for every limit number α，

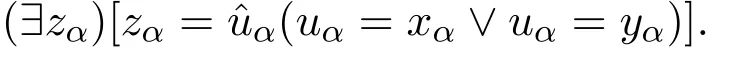
AxVI.The axiom of foundation：

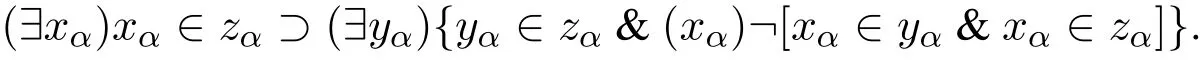
AxVII.The axioms of bounded order：if α＜β and xα∈yβ+1，then（∃zβ）（zβ= xα）；if α＞β，xα∈yβ，and β is of the nonsuccessor kind，then（∃zβ）（zβ=xα）.

Ri1.p∨［q∨（r∨s）］→p∨［r∨（q∨s）］.

Ri2.p∨（q∨r）→p∨（r∨q）.

Ri3.p∨p→p.

Ri4.q→p∨q.

Ri5.¬p∨q→¬（p∨p）∨q.

Ri6.p∨q，¬q∨r→p∨r.

Ri7.If b is a term of order α，q∨F（b）→q∨（∃uα）F（uα）.

Ri8.If vαdoes not occur in q，¬F（vα）∨q→¬（∃vα）F（vα）∨q.

The system Σ is the union of all the partial systems Σα；where，for each α，Σαis the part of the above symbolism that contain only variables and sets of order≤α. Strictly speaking Σ is a schema of formal systems or a recipe for making formal systems whenever an ordinal α is given.It has many peculiarities；for instance，all sets of Σ are enumerable in Σ，axiom of choice are provable in Σ，certain forms of the continuum hypothesis are provable in Σ and certain other forms are refutable in Σ，and Gödel famous constructions do not yield directly any propositions which are undecidable in the theory Σ.In detail，see Hao Wang's book A Survey of Mathematical Logic，pp.559-623.

2.2∃∀∃and Wang's domino theory

The decision problem of first order logic is to find a general method by which，given any logical schema，one can decide whether it is satisfiable.This general problem is known to be unsolvable.There remains the problem of deciding subclasses of the class of logical schemata.The most familiar classification is by using the class of formulas in the prenex form.Every prenex class is either decidable or a reduction class（and hence undecidable）.

On the side of prenex form reduction class，Hao Wang obtained a surprising result in 1961 which unites the interesting previously known reduction class.（see Proceedings of the National Academy of Sciences，U.S.A.48，pp.365-377 and ProceedingsoftheSymposiumontheMathematicalTheoryofAutomata，NewYork，April 1962，pp.23-55）.The result states that the schemata of the form

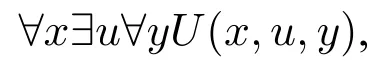
with dyadic predicates only（or even a single dyadic predicate plus monadic predicates）make up a reduction class for satisfiability.Thus，we get a general theorem，if we disregard identity：given any string of quantifiers Q1x1…Qkxk，the prefix class determined by it is a reduction class relative to satisfiability if and only if the string contains∃∀∃or∀∀∀∃as an order-preserving but not necessarily unbroken substring. Each prefix class that is not a reduction class is decidable and contains no axioms of infinity（i.e.no schemata which are satisfiable but not satisfiable in finite domains）.

The above-mentioned result is a brilliant achievement in the history of the development of mathematical logic.And，in 1961，Hao Wang founded a new algorithm theoryintheprocessofstudyingthedecisionproblemoffirstorderlogicthatisequivalent to Turing's machine theory.This theory attempts to study tiling problems which are very clear and simple in intuition.As mentioned above，these studies have led to results on more refined classifications of reduction problems and decision problems of first order.

Given a finite set of dominoes of the same size with edges colored，each domino in a different manner，suppose that there are infinitely many copies of each domino （domino type），and we are not permitted to rotate or reflect any domino.The question is how to cover up the whole infinite plane with such dominoes so that all corners fall on the lattice points with one very requirement，viz.，that two adjoining edges must have the same color.A set of dominoes is said to be solvable（in the infinite plane）if and only if there is some way of covering the whole plane by dominoes from the set. Some blocks consisting of copies of dominoes are given a special name.A torus of given domino set is a rectangle consisting of copies of some or all dominoes of the set such that：（a）adjoining edges always have the same color；（b）the sequence of colors on the bottom edges agree with that on the top edges；（c）the left edge agrees with the right edge.It is obvious that every set with a torus is solvable and has a periodic solution.A solution of a domino set is periodic if and only if there is a torus T such that by viewing T as a single domino，the solution is made entirely of copies of T.

The following domino problems are all known to be unsolvable：

1.The（unrestricted）domino problem.To find an algorithm to decide，for any given（finite）set of domino types，whether it is solvable.

2.The origin-constrained domino problem.To decide，for any given set P of domino types and a member C thereof whether P has a solution with the origin occupied by a domino of type C.

3.The diagonal-（row-，column-）Constrained domino problem.To decide，for anygivensetP ofdominotypeandasubsetQthereof，whetherP hasasolution with the main diagonal（the first row，the first column）occupied by dominoes of types in Q.

Hao Wang has given some elementary detail on these problems in Appendices A andCofhisbookPopularLecturesonMathematicalLogic（1979）.Infact，thehaltingproblem of Turing machines is reducible to the origin-constrained domino problem.

Using another description of domino problems，Hao Wang has established the correlation between domino problems and logical formula.Given a domino set P，we can find a formula Fpof the form：

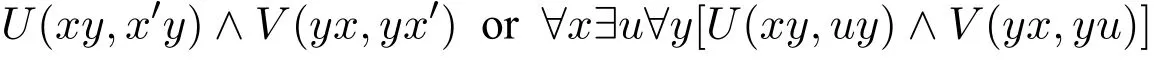
where U and V are truth-functional combinations of the components，such that P is solvable if and only if FPhas a model；conversely，given a formula F of the abovementioned form，we can find a domino set PFsuch that F has a model if and only if PFhasasolution.Hence，theunrestricteddominoproblemoftheclassofallformulas of above-mentioned form is unsolvable.

2.3Wang machines

Hao Wang published“A variant to Turing's theory of calculating machines”in 1957（in Journal of Association for Computing Machinery，vol.4）.This paper proposes two kinds of ideal computers：the machine B and W（or P）which are“the first formulation of Turing machine theory in terms computer-like models”（M.Minsky，Computation：Finite and Infinite Machines，1967，p.200）.

There are many differences between Turing machines and modern digital computer.Among these are the use of instructions instead of state-symbol combinations and the fact that a Turing machine realizes a single algorithm while on a computer various programs can be written to realize diverse algorithms.The machine W and the machine B behave like digital computers in these two respects but is more similar to Turing machines in other ways.This model lies in a middle ground where basic features of complex computers are illustrated but the primitive apparatus is stripped to a bare minimum.

The imagined machine W is made up of four parts：

（1）An indefinitely expandable internal random-access（parallel）storage to store programs（each program is a finite sequence of instructions）.

（2）Anindefinitelyexpandablelineartape（aserialstorage），rolledintoasuccession of squares，to store input，output and intermediate results.For definiteness，assume that each square is only capable of two states：blank（contains 0）or marked（contains 1）.

（3）A control element that keeps track of the program step to be taken at each moment.

（4）A read-write head which，at each moment，is supposed to be scanning one and only one square on the tap，and which is capable of shifting one square（left or right），reading，and writing（marking or erasing）.

At each moment，the next operation of the machine W is determined by the instruction of the program under attention of the control element，together with the content（blank or marked）of the square under scan.The machine W can perform five kinds of operations in accordance with these two factors，corresponding to the five types of basic instructions：

（1）→shift the head one square to the right.

（2）←shift left.

（3）∗mark the square under scan.

（4）eerase the square under scan.

（5）C（n）a conditional transfer.

The machine B is obtained from the machine W by deleting the erase operation.In the machine，a symbol once written will never be changed.In fact，since we use only two symbols，the machine B can only change blank square in its tapes to 1's，but cannot change a 1 back to a blank.

Wang proved that all recursive functions are B-computable，and so established the equivalence or coextensiveness of Turing computability and B-computability in the sense that a function is Turing computable if and only if it is B-computable.The machine B has universality.It is adequate for dealing with functions of numbers. This is true for functions of words as well.

2.4Computer proof of theorems

In the summer of 1958，Wang wrote three programs dealing with the first order logic；some loose ends were tied up in the autumn of 1959.These results were published in two papers at the beginning of 1960，generating considerable interest：“Toward mechanical mathematics”（written in the autumn of 1958），IBM Journal，vol.4（1960）；“Proving theorems by pattern recognition I”，Communications ACM，vol.3（1960）.The programs were written in a rather primitive language（SAP，the share assembly programming language）and on a small，slow machine（the IBM 704）. As is well known，the first order logic is undecidable.Yet all the theorems（over 350）of the first order logic in Principia Mathematica were proved in less than nine minutes.A surprising realization is that all the theorems of the first order logic actually proved in PM are of a rather trivial sort because they all belong to a simple decidable subdomain.This phenomenon points to the desirability of selecting appropriate subdomain or partial methods for a theory which is either undecidable or not practicably decidable.It is reported that when Russell heard about an account of some far less satisfactory result on proving theorems of PM by computers，he wrote：

“IwishWhiteheadandIhadknownofthispossibilitybeforebothwasted

ten years doing it by hand.I am quite willing to believe that everythingin deductive logic can be done by a machine.”（Ronald W.Clark，The life of Bertrand Russell，1976，p.548）

When Wang commented the progress of computer proof of theorem，he wrote：

“Since 1960，there have been a number of studies concerned with proving theorems on computers.Unfortunately a majority of published papers seem to center around the first order logic and primarily to elaborate a general theorem of Herbrand's on the first order logic.In my option，no striking results have appeared along this direction，which is different from what I envisaged as the promising approach.I believed and continue to believe that in order to prove theorems in a special mathematical discipline，one must pay special attention to what is specific to the subject.For example，in dealing with number theory one must pay special attention to mathematical induction perhaps in the form of trying to derive a contradiction from the assumption that there is a least counterexample to the general proposition∀xPx to be derived.”（Popular Lecture of Mathematical Logic，1981，pp.47-48.）

Wang won Milestone Prize of mechanical proof of mathematical theorems in 1982 because of his creative work.

2.5Logic semantics

Hao Wang's paper“Truth definitions and consistency proof”discussed various conceptions in connection with the truth definition，in order to separate two different elements of a truth definition，he distinguished between a normal truth definition and a abnormal truth definition，introduced several translatability concept：and the results in the paper bring out more clearly than usual certain features in the procedures of constructing truth definitions and proving consistency.Wang's paper was an important contribution to the research of logical semantics；it could be compared to Tarski's well-known paper in 1933.In his paper Hao Wang gives six axiomatic systems S1，S2，S3，S4，S5，and S6，which are relevant with each other but different in strength，and his research is the problem of the construction，in one system of the truth definition and the consistency proofs via truth definitions in another system.The six systems S1-S6given in the paper could be outlined in a simply way as follows：

S3is a very weak set theory in which we assume merely the null set and the sets constructedoutofit；S3hasthesamenotationsastheordinaryZemelosettheory（one primitive predicate and one kind of variable only）and contains merely the axiom of extensionality，theaxiomofnullsetandanaxiomsayingthatbyaddinganewmember to given set，we have again a set.

S1is a second-order predicate calculus with S3as its theory of individuals；S1contains both predicative and impredicative classes of sets of S3.

S6is obtained from S3by adding the Aussonderungs axiom（a schema）.

S2is related to S6as S1is to S3except that S2contains only predicative classes of the sets of S6and that the Aussonderungs axiom in S2becomes a single axiom（the intersection of a set and a class is again a set）involving a free class variable.S2is the partial system of the NB，and S6is related to S2as ZF is to NB.

S4is roughly the ordinary Zermelo set theory，and S5is related to S4as S3is to S1.In S5the Aussonderungs axiom remains the same as in S4and no references to classes are allowed in defining sets（or elements）.S′5is a further extension of S5where the restriction is removed and the new Aussonderungs axiom states（as in S2）that the intersection of a set and a class is again a set.

There are many results concerning the systems S1-S6in the paper，among them we give the following theorems and results as example.

Theorem I.In S1we can construct a truth definition for the Zermelo set theory.

Theorem II.In S2we can construct a truth definition for Zermelo set theory.

By Theorem I and II，S1and S2each contain a truth definition for S3.Moreover，all the theorems of S3are also theorems of S1and S2.

Theorem IV.⊢S1Con（S3）.

The consistency of S3can be formally proved in S1.On other hand，in all probability no consistency proof for S3can be formalized in S2.

S5contains a truth definition of S4as well as all the theorems of S4.For the question of proving Con（S4）in S5，the provability or unprovabilility of Con（S4）in S5remains an open question.If we extend the system S5to the system S′5，then a proof of Con（S4）in S′5can indeed be obtained，We have：

4.13⊢s′5Con（S4）.

We can prove in place of Con（S3）the following metatheorem about S2which tells us that no given definite proof of S3can be a proof of the sentence∀x2∃x1（x1∈x2）of S3：

4.14Ifnisaconstant，then⊢s2−pr（n，m0）（m0istheGödelnumberofthesentence ∀x2∃x1（x1∈x2））.

This depends on the fact that if we consider only the individual number one by one，we need not make the inductions.（In the proof of Theorem IV，the inductionsare indispensable.）

There are two other Theorems（V，VI）concerning systems R，R′of number theory.

The connections between S2and S6are of special importance because S2is related to S6in the same way as NB is to ZF.When two systems S′and S are related in the same way as NB is to ZF，we say that S′is a predicative extension of S.Thus，S2is a predicative extension of S6.Theorem II，the result 4.17 are concerned with the relations between systems and their predicative extensions.

S1and S3，S5and S4，R and R′are all related to each other in the same way. When S′and S are thus related，we say that S′is an impredicative extension of S. Thus，S1isanimpredicativeextensionofS3，S5isoneofS4，R′isoneofR.Themain results in Wang's paper（including the Theorems I，IV，V，and VI）are all concerned with the relations between systems and their impredicative extensions.The interest and validity of these results depends largely on the relative consistency of a system and its impredicative extension，first established by Hao Wang.It seems proper to say that the relative consistency of a system and its predicative extension is much less surprising than that of a system and its impredicative extension.

3　Contributions to Philosophy

Starting with philosophical research since his study in the university，Hao Wang has written many philosophical works and made important contributions to philosophy and especially to mathematical logic and computer science for quite a long time，many of his works of mathematical logic are motivated by philosophy and concurrently of logical and philosophical significance.For example，the motivation for the fundamental work of predicative analysis“The Axiomatization of Mathematics”，which was written in 1953，is philosophical，as he says himself.And also his important papers of mathematical philosophy such as“Process and Existence in Mathematics”.It is not possible here to make a systematic and overall introduction to his philosophy because of the shortage of our research of his philosophy，which is to some extend quite difficult to grasp.Being not the kind of philosopher who establishes philosophical systems，he has no special works about fundamental philosophy such as metaphysics and epistemology，etc.

He wrote in the Preface to From Mathematics to Philosophy（MP）：

“This book certainly makes no claim to a philosophical theory or a sys

tem of philosophy.In fact，for those who are convinced that philosophy

should yield a theory，they may find here merely data for philosophy.I

believe，in spite of my reservations about the possibility of philosophy as

a rigorous science，that philosophy can be relevant，serious，and stable.

Philosophy should try to achieve some reasonable overview.There ismore philosophical value in placing things in their right perspective than in solving specific problems.”（p.X）

Hao Wang often shows his points of view and makes his contributions to philosophy by studying and analyzing special problems（e.g.，the concept of set）in the fields of logic and mathematics，or by discussing and criticizing other philosophies（such as empiricism and analytic philosophy in a wide sense），or by reflecting on Gödel. This might be said to be his style of philosophy，which makes it difficult to grasp his philosophy.So we would only make a simple introduction.

Hao Wang holds that philosophy is not only a proper science，but also has a special position in the human knowledge，and that it could not be reduced to the research of logic or that of language.This point of view is related to the influence of the Chinese culture upon him.Hao Wang says：

“My professional training is nearly all in western philosophy（much of it even logic-oriented），yet my formative years were lived in China.I have tried hard but have not been able to shake off my early conviction that philosophy is not just one subject more or less like any other，but something special.Even today such a belief，I think，persists in China.”

“IfindmyselfattachedtotheChinesetraditionofmixingtogetherphilosophy，literature，and history，a tradition that is conditioned by the central concerns of its philosophy；the interest in politics ties it to history，the inter interpretation of texts merges philosophy with its history，and the concern with the unity of nature and person overlaps with art and literature”.（Beyond Analytic Philosophy，（BAP），p.194）

It is well known that Gödel has an important influence upon Hao Wang in philosophy. Hao Wang agrees with Gödel on many important philosophical issues，and especially those of mathematical philosophy，except of a very important aspect.Hao Wang holds that philosophy should derive nourishment from the human experiences in the past two or three hundred years，while Gödel thinks that most of these new experiences have nothing to do with the basic issues；that we should concentrate ourselves on the research of basic philosophy and not divert our attention for other aspects of philosophy.And Gödel has the idea that once a definite theory is found for the basic philosophy，what remains is only to know how to apply this theory to the non-basic aspects of various fields，while Hao Wang insists that there is，according to the experiences in the past，little possibility for the basic philosophy required by Gödel to completely come true.Hao Wang says：

“What I have in mind is a sort of skeleton system that gives each part its due and reflects the current state of human understanding in a fairly faithful and structured manner.”（BAP，p.2）Calling his philosophical outlook in general the substantial factualism，Hao Wang holds that philosophy should respect the existing knowledge that has overwhelming importanceforphilosophy.AstothequestionputbyKant-“WhatcanIknow？”，Hao Wang holds that a question of more inspiration is：what we know？And he says：“We know more about what we know than how we know.”（MP，p.1）What he thinks of is mainly about mathematical and scientific knowledge.He holds that at the present stage of human knowledge mathematics is especially adapted to the general discussions about conceptual thinking.In his From Mathematics to Philosophy he chooses some basic concepts in fields of logic and mathematics for closer examination，such as logical truth，set，mechanical procedure，etc.，illustrating a general position on the philosophy of knowledge.But he says that

“Initsgeneralconceptionitisnotintendedtoapplyexclusivelytoknowledgeintheexactsciences.Wearealsointerestedinlessexactknowledge and less clearly separated-out gross facts.”（MP，p.2）

Factualism is also interested in how we know in the sense of desiring to consider the basic aspects of factual process of knowing.Hao Wang says：

“The most important single aspect is the process by which a proposition or theory becomes accepted as part of human knowledge or a particular individual's knowledge.This factor of acceptance is the central anthropocentric component of factualism.”（MP，pp.19-20）

This substantial factualism might be called anthropocentric magnifactualism as well.

Substantial factualism is opposed to positivism and empiricism（particularly the twodifferentdirectionsofR.CarnapandW.V.Quine）andlinguisticphilosophy.Hao Wang says that positivism does not have enough respect for gross scientific facts.In particular，Carnap's position often lays too much emphasis on empty artificial structures to the neglect of the serious factual（or rather conceptual）content.Hao Wang seems to admit that he has some agreement with Quine on factualism but he emphasizes their disagreements in his discussion about Quine's philosophy.Criticizing the traditional epistemology in a place，Hao Wang says：

“The central bias of factualism implies a dissatisfaction with epistemology as it is commonly pursued on the ground that it is too abstract and too detached from actual knowledge”（MP，p.19）.

ThismightalsobetakenasacriticismonQuine'sprojectofnaturalisticepistemology. Hao Wang proposes to replace epistemology with“epistemography which，roughly speaking，is supposed to treat of actual knowledge as phenomenology proposes to dealwithphenomena”（ibid.）HaoWangholdsthatlinguisticphilosophyonthewhole tendstobepiecemeal（lackinginsubstance）andpayslittlethat“substantialfactualism is a useful antidote to these fashionable trends”（MP，p.3）.He says：“The sermon is to take actual knowledge more seriously in order to correct a fashionable tendency toward a form of Neo-Scholasticism.”（MP，p.15）

The analysis and discussion that Hao Wang has made in MP about the concepts of set，mind，machine，etc.，including his introduction and interpretation of Gödel's points of view about these problems，are undoubtedly of great importance for mathematical philosophy and cognitive philosophy in general.However we do not discuss them here.

Underlying MP is undoubtedly a rejection of empiricism as unable to give an adequate account of mathematics.And a major theme of BAP“is that analytic empiricism does not and cannot give an adequate account of mathematics.”（p.XII）

It has been taken as a problem for empiricism for quite a long time.The Vienna Circle，especially Carnap's logic and mathematical philosophy，think that a way of solution has been found，that is，to reduce mathematics to logic.According to Wittgenstein's idea of regarding logical propositions as tautologies，they are“necessarily true”，because they say nothing.Quine does not accept Carnap's position and insists his own version of empiricism.Hao Wang holds that the difference between Quine and Carnap is an internal revolt between them.He says：

“WhatisfundamentalinCarnapandQuineis，Ithink，nottwodogmasof analyticity and reductionism which separate them，but rather the denial of any autonomy to conceptual knowledge which unites them.”（BAP，p. 11）

He calls Carnap and Quine as analytic empiricists and proposes to label the intersection of their views on analysis and empiricism the two commandments of analytic empiricism.

Wang states the“two commandments of analytic empiricism”as follows（BAP，p.12）：

（A）Empiricism is the whole of philosophy and there can be nothing（fundamental）which could be properly called conceptual experience or conceptual intuition.

（B）Logic is all important for philosophy，but analyticity（even necessity）can only mean truth by convention.

Hao Wang holds that the unresolved and unresolvable difficulty for analytic empiricists is a problem put forward by mathematics to empiricism.He asserts：（A）EmpiricisminthesenseofCarnaporQuinecannotgiveanadequateaccountofmathematics.

Hao Wang proves the proposition（A）separately with regard to Carnap and Quine.According to him，Carnap maintains：

（C1）Logicism：mathematics is reducible to logic.

（C2）Analyticity：Logical truth is analytic.

（C3）Conventionalism：analyticalpropositionsaretruebyconventionand，therefore，void of content.

HaoWangholdsthat（C1）commitsCarnapto（1b）：Logicincludessettheory.As for analyticity，Hao Wang says that of the various senses of the term analytic Gödel singles out two significant ones：（2a）Tautological.（2b）Analytic.“A proposition is called analytic if it holds，owing to the meaning of the concepts occurring in it，where this meaning may perhaps be undefinable（i.e.，irreducible to anything more fundamental）”.In this sense the axioms and theorems of mathematics，set theory，and logic are all analytic，but need not，as a result，be“void of content”.Hao Wang holds that，（C2），combine with（C1），appears to commit Carnap also to something Like （2b）.Then Hao Wang provides an analysis for Carnap's view of determinism：what is asserted in mathematics can be interpreted to comprise syntactical conventions and their consequences.He says：

“From these considerations it follows that those who accept（C1）and （C2）must reject（C3）and replace it by（2b），or at least by some（weaker）variant of it which ceases to deprive all analytic propositions of their ‘content'.”（BAP，p.16）

And further Hao Wang puts forward three propositions（G1），（G2），（G3）by what he wants to simplify the discussion，and among which（G3）runs as follows：Analytic is understood in the sense of（2b）so that analytic propositions need not be void of content；indeed，mathematics（and logic）have‘real'content.With further inferences Hao Wang concludes：

“InthecaseofCarnap，heseemscommitted（G3）also，andthisfactproves proposition（A）for Carnap's type of empiricism.”（BAP，p.16）

As for Quine，Hao Wang holds that Quine obliterates the distinction between mathematics and natural sciences，and denies the autonomy of mathematics.Hao Wang shows that Quine's holism could give no reasonably satisfactory account，by a number of examples that include：the decisive importance of the nonfinitary concept of arithmetic truth for Gödel's discovery of the incompleteness theorems.Hao Wang asks：

“HowisQuine'sholismtogiveaconvincingaccountofthis‘mysterious' yet stable intuition of the nonfinitary concept of arithmetic truth？”（BAP，p.18）

Hao Wang says：

“By giving up the first commandment of（analytic）empiricism，one is in a position to view the wealth of the less concrete mathematical facts and intuitions as a welcome source of material to enrich philosophy，instead of an irritating mystery to be explained away.”（BAP，p.19）

Hao Wang says：

“In philosophy I tend to meander and ramify and be noncommittal…As a result，there is usually a real or apparent lack of focus.”（BAP，p.2）

We feel that we could probably say with supplement that this makes some of his discussions inconclusive.Hao Wang often discusses philosophical issues in such a way，that he raises questions and states various considerations and views about the questionsandtheoreticalcommitments.Hisstyleofsuchakinddoesmakethereaders disappointed who want to get definite conclusions.But the way in which he deals with problems has also a good point，that is，it could avoid excessive simplification andmakingcarelessconclusions，sothatthereaderscouldhavetheirownconclusions through deep considerations.

In a summary we have only a sketchy introduction to Hao Wang's philosophy without mentioning his two books about Gödel.We hope that by our introduction the readers could have a general impression：Hao Wang's philosophical works and contributions are of important significance not only for those who share his position，but also for those who have quite different points of view.

A Bibliography of Hao Wang2Original annotation：M.Grossi，M.Link，K.Makkai，and C.Parsons：“A Bibliography of Hao Wang，”Philosophia Mathematica（III）00（2012），pp.1-17.The original of this bibliography appeared in Philosophia Mathematica（3）6（1998），pp.25-38.The present version incorporates the updating and corrections embodied in the reprint in Hao Wang，Logician and Philosopher，edited by Parsons and Link（London：College Publications，2011）.Further corrections and additions should be sent to Charles Parsons.，3Original annotation：M.Grossi，M.Link，K.Makkai，and C.Parsons：“A Bibliography of Hao Wang，”Philosophia Mathematica（III）00（2012），pp.1-17.The original of this bibliography appeared in Philosophia Mathematica（3）6（1998），pp.25-38.The present version incorporates the updating and corrections embodied in the reprint in Hao Wang，Logician and Philosopher，edited by Parsons and Link（London：College Publications，2011）.Further corrections and additions should be sent to Charles Parsons.

1944“新理学的形而上学系统”，“哲学评论”，第9卷第3期，第39-62页。

1945“语言和形而上学”，“哲学评论”，第10卷第1期，第35-38页。English translation，［2005］.

1947a“Notesonthejustificationofinduction”，JournalofPhilosophy44，701-710. Reprinted in［1974a］，Appendix.

1947b“A note on Quine's principles of quantification”，Journal of Symbolic Logic 12，130-132.

1948a“A new theory of element and number”，Journal of Symbolic Logic 13，129-137.Reprinted in［1962a］as Chapter XX，Section 2.

1948b“The existence of material objects”，Mind 57，488-490.Reprinted in ［1974a］，Appendix.

1948cReview of Eugene Shen，Luen li hsueh（Logic），Journal of Symbolic Logic 13，215-216.

1949a“A theory of constructive types”，Methodos 1，374-384.

1949b“New hopes and old fears”，Chinese Student Opinion 3，No.4（July 1949），1-3.

1949c“On Zermelo's and von Neumann's axioms for set theory”，Proceedings of the National Academy of Sciences，U.S.A.35，150-155.

1949dReviewofHermannWeyl，PhilosophyofMathematicsandNaturalScience，Physics Today 2，No.11（November 1949），35-36.

1950a“Remarks on the comparison of axiom systems”，Proceedings of the National Academy of Sciences，U.S.A.36，448-453.Reprinted in［1962a］in Chapter XVII.

1950b“The non-finitizability of impredicative principles”，Proceedings of the National Academy of Sciences，U.S.A.36，479-484.

1950c“On scepticism about induction”，Philosophy of Science 17，333-335. Reprinted in［1974a］，Appendix.

1950d“A proof of independence”，American Mathematical Monthly 57，99-100.

1950e“A formal system of logic”，Journal of Symbolic Logic 15，25-32. Reprinted in［1962a］as Chapter XVI，Section 5.

1950f“Existence of classes and value specification of variables”，Journal of Symbolic Logic 15，103-112.Reprinted in［1962a］in Chapter XX，Section 1.

1950g（With J.Barkley Rosser）“Nonstandard models for formal logics”，Journal of Symbolic Logic 15，113-129.

1950h“Set-theoreticalbasisforrealnumbers”，JournalofSymbolicLogic15，241-247.Reprinted in［1962a］as Chapter XX，Section 3.

1951a“Arithmetic models for formal systems”，Methodos 3，217-232.

1951b“Arithmetic translations of axiom systems”，Transactions of the American Mathematical Society 71，283-293.Reprinted in［1962a］as Chapter XIII，Section 4.

1951cReview of Alfons Borgers，“Development of the notion of set and of the axioms for sets”，Journal of Symbolic Logic 16，152-153.

1951dReview of Paul Lorenzen，“Algebraische und logistische Untersuchungen über freie Verbände”，Journal of Symbolic Logic 16，269-272.

1951eReview of Shen Yu-Ting，“Yu-yen，su-hsiang，yu i-i（Language，thought，and meaning）”，Journal of Symbolic Logic 16，302-303.

1951fReviewofYinFu-Sheng，“Characteristicsofscientificempiricismandcomments thereon”（in Chinese），Journal of Symbolic Logic 16，304.

1952a“Truth definitions and consistency proofs”，Transactions of the American MathematicalSociety73，243-275.Reprintedin［1962a］asChapterXVIII.

1952b“Negative types”，Mind 61，366-368.

1952c“Logic of many-sorted theories”，Journal of Symbolic Logic 17，105-116. Partially incorporated into Chapter XII of［1962a］and reprinted in［1990a］.

1952d“The irreducibility of impredicative principles”，Mathematische Annalen 125，56-66.Reprinted in［1962a］in Chapter XVII.

1952eReviewofArnoldSchmidt，“DieZulässigkeitderBehandlungmehrsortiger TheorienmittelsderüblicheneinsortigenPrädikatenlogik”，JournalofSymbolic Logic 17，76.

1953a（With Robert McNaughton）Les systèmes axiomatiques de la théorie des ensembles.Collection de Logique Mathématique，Série A，No.4.Paris：Gauthier-Villars.Louvain：E.Nauwelaerts.

1953b“Between number theory and set theory”，Mathematische Annalen 126，385-409.Reprinted in［1962a］as Chapter XIX.

1953c“Certain predicates defined by induction schemata”，Journal of Symbolic Logic 18，49-59.Reprinted in［1962a］as Chapter XXI.

1953d“What is an individual？”，Philosophical Review 62，413-420.Reprinted in ［1974a］，Appendix.

1953e“The categoricity question of certain grand logics”，Mathematische Zeitschrift 59，47-56.

1953f“Quelques notions d'axiomatique”，Revue philosophique de Louvain 51，409-443.

1953g“A problem on propositional calculus（problem 6）”，Journal of Symbolic Logic 18，186.

1953hReview of G.Kreisel，“Note on arithmetic models for consistent formulae of the predicate calculus”，Journal of Symbolic Logic 18，180-181.

1954a“Aquestiononknowledgeofknowledge”，Analysis14，142-146.Reprinted in［1974a］，Appendix.

1954b“The formalization of mathematics”，Journal of Symbolic Logic 19，241-266.Reprinted in［1962a］as Chapter XXIII.

1955a“Undecidablesentencesgeneratedbysemanticparadoxes”，JournalofSymbolic Logic 20，31-43.Reprinted in［1962a］as Chapter XXII.

1955b“Notes on the analytic-synthetic distinction”，Theoria 21，158-178.Incorporated into Chapter VIII of［1974a］.（“有关分析命题与综合命题的区别的札记”，“哲学译丛”，1982年第1期，第28-38页。）

1955c（With G.Kreisel）“Some applications of formalized consistency proofs”，Fundamenta Mathematicae 42，101-110.Summarized with part II（［1958c］）in Chapter XV，Section 2，of［1962a］.

1955d“On denumerable bases of formal systems”，in Th.Skolem et al.，Mathematical Interpretation of Formal Systems，pp.57-84.Amsterdam：North-Holland.

1955e“On formalization”，Mind 64，226-238.Reprinted in［1962a］as Chapter III and in［1990a］.Also reprinted in Irving M.Copi and James A.Gould （eds.），Contemporary Readings in Logical Theory.New York：Macmillan，1967.

1957a“The axiomatization of arithmetic”，Journal of Symbolic Logic 22，145-158.Reprinted in［1962a］as Chapter IV.

1957b“A variant to Turing's theory of computing machines”，Journal of the AssociationforComputingMachinery4，63-92.Reprintedin［1962a］asChapter VI.

1957c“Universal Turing machines：An exercise in coding”，Zeitschrift für mathematische Logik und Grundlagen der Mathematik 3，69-80.Reprinted in ［1962a］as Chapter VII.

1957d（With A.W.Burks）“The logic of automata”，Journal of the Association for Computing Machinery 4，193-218，279-297.Reprinted in［1962a］as Chapter VIII.

1958a“Eighty years of foundational studies”，Dialectica 12，466-497.Also in Logica：Studia Paul Bernays dedicate，pp.262-293.Neuchätel：Editions du Griffon，1959.Reprinted in［1962a］as Chapter II.

1958b“Alternative proof of a theorem of Kleene”，Journal of Symbolic Logic 23，250.

1958c（With G.Kreisel）“Some applications of formalized consistency proofs. Part II”，Fundamenta Mathematicae 45，334-335.Summarized with ［1955c］in Chapter XV，Section 2，of［1962a］.

1959a“Ordinalnumbersandpredicativesettheory”，Zeitschriftfürmathematische Logik und Grundlagen der Mathematik 5，216-239.Reprinted in［1962a］as Chapter XXV.

1959b“Circuit synthesis by solving sequential Boolean equations”，Zeitschrift für mathematische Logik und Grundlagen der Mathematik 5，291-322. Reprinted in［1962a］as Chapter X.

1959c（With G.Kreisel and J.R.Shoenfield）“Number-theoretic concepts and recursive well-orderings”，Archiv für Mathematische Logik und Grundlagenforschung 5，42-64.

1960a“Toward mechanical mathematics”，IBM Journal of Research and Development 4，2-22.Reprinted in［1962a］as Chapter IX.Also reprinted in K. Sayre and F.Crosson（eds.），The Modelling of Mind，pp.91-120.University of Notre Dame Press，1963.（Paperback edition，New York：Simon and Schuster，1968.）Also reprinted in Jörg Siekmann and Graham Wrightson（eds.），Automation of Reasoning 1：Classical Papers on Computational Logic，1957-1966.Springer-Verlag，1983.

1960b“Proving theorems by pattern recognition，Part I”，Communications of the Association for Computing Machinery 3，220-234.Reprinted together with Part II（［1961a］），as Bell Technical Monograph 3745.Also reprinted in Siekmann and Wrightson，op.cit.（see［1960a］），and in［1990a］.

1960c“Symbolic representations of calculating machines”，Summaries of Talks Presented at the Summer Institute for Symbolic Logic，Cornell University，1957，pp.181-188.Princeton，N.J.：Institute for Defense Analyses，Communications Research Division.

1960d“Remarks on constructive ordinals and set theory”，Summaries of Talks Presented at the Summer Institute for Symbolic Logic，Cornell University，1957，pp.383-390.Princeton，N.J.：Institute for Defense Analyses，Communications Research Division.

1960eReview of Moh Shaw-Kwei，“Simplified introduction to intuitionistic logic”（in Chinese），Journal of Symbolic Logic 25，181.

1960fReview of Moh Shaw-Kwei，“About the rules of procedure”（in Chinese），Journal of Symbolic Logic 25，182.

1960gReview of Moh Shaw-Kwei，“Axiomatization of manyvalued logical systems”（in Chinese），Journal of Symbolic Logic 25，181-182.

1960hReview of Moh Shaw-Kwei，“On the explicit form of number-theoretic functions”（in Chinese），Journal of Symbolic Logic 25，182.

1960iReview of Moh Shaw-Kwei，“On the definition of primitive recursive functions”（in Chinese），Journal of Symbolic Logic 25，182.

1960jReview of Moh Shaw-Kwei，“Some axiom systems for propositional calculus”（in Chinese），Journal of Symbolic Logic 25，182-183.

1960kReview of Moh Shaw-Kwei，“On the explicit form of general recursive functions”（in Chinese），Journal of Symbolic Logic 25，183.

1961a“Proving theorems by pattern recognition.Part II”，Bell System Technical Journal 40，1-41.Also appeared，together with Part I（［1960b］），as Bell Technical Monograph 3745.Reprinted in［1990a］.

1961b“Process and existence in mathematics”，in Y.Bar-Hillel，E.I.J.Poznanski，M.O.Rabin，and A.Robinson（eds.），Essays on the Foundations of Mathematics，Dedicated to Prof.A.A.Fraenkel on His 70th Anniversary，pp. 328-351.8 Jerusalem：Magnes Press，The Hebrew University of Jerusalem. Partly incorporated into［1974a］，Chapter VII，and reprinted in［1990a］.

1961c“The calculus of partial predicates and its extension to set theory I”，Zeitschrift für mathematische Logik und Grundlagen der Mathematik 7，283-288.Reprinted in［1990a］.

1961d“An unsolvable problem on dominoes”，Report BL-30，The Computation Laboratory，Harvard University，1-5.

1962aA Survey of Mathematical Logic.Peking：Science Press.Also Amsterdam：North-Holland Publishing Company，1963.Reprinted as Logic，Computers and Sets.New York：Chelsea，1970.

1962b（With A.S.Kahr and Edward F.Moore）“Entscheidungsproblem reduced to the∀∃∀case”，Proceedings of the National Academy of Sciences，U.S.A. 48，365-377.

1962c（With Burton Dreben and A.S.Kahr）“Classification of AEA formulas by letter atoms”，Bulletin of the American Mathematical Society 68，528-532.

1962d（With A.S.Kahr）“A remark on the reduction problem with application to the∀∃∀formulas”（Abstract），Notices of the American Mathematical Society 9，130.

1963a“Mechanical mathematics and inferential analysis”，in p.Braffort and D. Hirschberg（eds.），Computer Programming and Formal Systems，pp.1-20. Amsterdam：North-Holland.Reprinted in［1990a］.

1963b（With M.O.Rabin）“Words in the history of a Turing machine with a fixed input”，Journal of the Association for Computing Machinery 10，526-527.

1963c“Dominoes and the∀∃∀case of the decision problem”，in Jerome Fox et al.（eds.），Proceedings of the Symposium on the Mathematical Theory of Automata，New York，April 1962，pp.23-55.Brooklyn：Polytechnic Press. Reprinted in［1990a］.

1963d“Tag systems and lag systems”，Mathematische Annalen 152，65-74.

1963e“Themechanizationofmathematicalarguments”，inN.C.Metropolis，A.H. Taub，JohnTodd，andC.B.Tompkins（eds.），ExperimentalArithmetic，High Speed Computing and Mathematics，pp.31-40.Proceedings of Symposia in Applied Mathematics，vol.15.Providence：American Mathematical Society.Reprinted in［1990a］.

1963f（With A.S.Kahr）“Degrees of RE models of∀∃∀formulas”（Abstract），Notices of the American Mathematical Society 10，192-193.

1963gReview of William and Martha Kneale，The Development of Logic，Mathematical Reviews 26，450.

1964a（With W.V.Quine）“On ordinals”，Bulletin of the American Mathematical Society 70，297-298.

1964b“Remarks on machines，sets and the decision problem”，in J.N.Crossley andM.A.E.Dummett（eds.），FormalSystemsandRecursiveFunctions，pp. 304-320.Amsterdam：North-Holland.Reprinted in［1990a］.

1964cCritique［of Robert R.Kofhage，“Logic for the Computer Sciences”］，Communications of the ACM 7，218.

1965a“Russell and his logic”，Ratio 7，1-34.Reprinted，revised，as Chapter III of ［1974a］.

1965b“Formalization and automatic theorem proving”，in Wayne A.Kalenich （ed.），Proceedings of IFIP Congress 65，pp.51-58.Washington，D.C.：Spartan Books.Reprinted in［1990a］.

1965c“Note on rules of inference”，Zeitschrift für mathematische Logik und Grundlagen der Mathematik 11，193-196.

1965d“Logic and computers”，American Mathematical Monthly 72，135-140. Reprinted as Chapter IX，Section 6，of［1974a］and in［1990a］.

1965e“Games，logic and computers”，Scientific American 213，No.5（November 1965），98-106.Reprinted in［1990a］.

1966a（With S.A.Cook）“Characterizations of ordinal numbers in set theory”，Mathematische Annalen 164，1-25.

1966b（With Kenneth R.Brown）“Finite set theory，number theory and axioms of limitation”，Mathematische Annalen 164，26-29.

1966c（withKennethR.Brown）“Shortdefinitionsofordinals”，JournalofSymbolic Logic 31，409-414.

1966d“Russell and philosophy”，Journal of Philosophy 63，670-673.Partly incorporated into［1974a］，Chapter XI，Section 4.

1967a“Natural hulls and set existence”，Zeitschrift für mathematische Logik und Grundlagen der Mathematik 13，175-182.Reprinted in［1990a］.

1967b“On axioms of conditional set existence”，Zeitschrift für mathematische Logik und Grundlagen der Mathematik 13，183-188.Reprinted in［1990a］.

1967c“A theorem on definitions of the Zermelo-von Neumann ordinals”，Zeitschrift für mathematische Logik und Grundlagen der Mathematik 13，241-250.Reprinted in［1990a］.

1967dIntroductory note to Andrei Nikolaevich Kolmogorov，“On the principle of excluded middle”，in Jean van Heijenoort（ed.），From Frege to Gödel，A Source Book in Mathematical Logic，1879-1931，pp.414-416.Cambridge，Mass.：Harvard University Press.

1970a“A survey of Skolem's work in logic”，in Th.Skolem，Selected Works in Logic，J.E.Fenstad（ed.），pp.17-52.Oslo：Universitetsforlaget.Incorporated，with additions and corrections by J.E.Fenstad，into［2009］.

1970b“Remarks on mathematics and computers”，in R.B.Banerji and M.D. Mesarovic（eds.），Theoretical Approaches to Nonnumerical Problem Solving，pp.152-160.Berlin：Springer-Verlag.Partly incorporated into［1974a］，Chapter IX.Reprinted in［1990a］.

1970c“On the long-range prospects of automatic theorem-proving”，in M.Laudet，D.Lacombe，L.Nolin，and M.Schützenberger（eds.），Symposium on Automatic Demonstration，pp.101-111.Berlin：Springer-Verlag.Reprinted in ［1990a］.

1971a“Logic，computationandphilosophy”，L'agedelascience3，101-115.Partly incorporated into［1974a］，Chapter VII.Reprinted in［1990a］.

1971bLetter to the Editor.The New York Times，May 30，1971.

1972“中国之行的几点观感”，“新中国”，1972年第7期，第23-26、31页。

1973a“香港文化四十年”，“七十年代”，1973年第44期，第22-23页。

1973b（With Bradford Dunham）“A recipe for Chinese typewriters”，IBM report RC4521，September 5，1973.Published in Chinese；see［1976a］.（“中文打字机的秘诀”，“IBM报告RC4521”，1973年9月5日。）

1974aFrom Mathematics to Philosophy.London：Routledge&Kegan Paul. Chapter VI reprinted in Paul Benacerraf and Hilary Putnam（eds.），Philosophy of Mathematics：Selected Readings，2nd ed.Cambridge University Press，1983.Chapter VII reprinted with slight revisions in Thomas Tymoczko（ed.），New Directions in the Philosophy of Mathematics，pp. 131-152.Boston：Birkhäuser，1986.2nd ed.，Princeton University Press，1997.Chapter IX，Sections 3-4，reprinted（in English）in Christian Thiel （ed.），Erkenntnistheoretische Grundlagen der Mathematik，pp.332-337. Hildesheim：Gerstenberg Verlag，1982.

1974b“Metalogic”，in Encyclopaedia Britannica，Fifteenth edition，vol.11，pp. 1078-1086.Chicago：Encyclopaedia Britannica，Inc.incorporated into Chapter V of［1974a］.Reprinted in part in［1990a］.

1974c“Concerning the materialist dialectic”，Philosophy East and West 24，303-319.

1974dLetter to the Editor.The New York Times，June 18，1974.

1975a“Notes on a class of tiling problems”，Fundamenta Mathematicae 82，295-305.Reprinted in［1990a］.

1975bLetter to the Editor.Washington Post，November 1，1975.

1976a（With Bradford Dunham）“A recipe for Chinese typewriters”（Chinese），Dousou Bimonthly，No.14（March 1976），56—62.Chinese version of ［1973b］.（“中文打字机的秘诀”，“抖擞双月刊”，1976年3月第14期，第56-62页。）

1976b（With Bradford Dunham）“Toward feasible solutions of the tautology problem”，Annals of Mathematical Logic 10，117-154.Reprinted in［1990a］.

1976cLetter to the Editor.The New York Times，February 9，1976.

1977a“Large sets”，in Robert E.Butts and Jaakko Hintikka（eds.），Logic，Foundations of Mathematics，and Computability Theory，pp.309-333.Dordrecht：Reidel.

1977b“ThesearchingsofLuXun”（Chinese），DousouBimonthly，No.19（January 1977），1-14.（“探寻鲁迅”，“抖擞双月刊”，1977年1月第19期，第1-14页。）Abridged version，The Seventies Monthly，No.85（February 1977），70-73.（“七十年代月刊”，1977年2月第85期，第70-73页。）

1977c“Dialectics and natural science”，Overseas Chinese Life Scientists Association Newsletter 1，No.2（March 1977），48-55.

1977d（With D.A.Martin）“Ranked matching and hospital interns”.Published in［1990a］，pp.275-289，but dated 1977.1978“Kurt Gödel's intellectual development”，Mathematical Intelligencer 1，No.3，182-184.（“库尔特·哥德尔的思想发展”，“自然科学哲学问题”，1980年第4期，第88-90页。）

1979a“Kurt Gödel and some of his philosophical views：On mind，matter，machine and mathematics”，Proceedings of the Roundtable on Aristotle，June 1978.Paris：UNESCO.

1979b“汉字的机械处理——兼谈信息传达技术”，“电子计算机动态”，1979年第6期，第1-4页。EnglishtranslationbyFanLanying，“Oninformation processing in the Chinese language”，in［1990a］.

1979c“今日中国及其60年以来的发展”，“广角镜周刊”，第86期，第32-49页。

1980“Kurt Gödel”，in McGraw-Hill Encyclopedia of Scientists and Engineers，pp.438-439.New York：McGraw-Hill.

1981aPopular Lectures on Mathematical Logic.Beijing：Science Press.Also NewYork：VanNostrandReinhold.ReprintedwithaPostscript，NewYork：Dover Publications，1993.Chinese translation，Beijing：Science Press，1981.（“数理逻辑通俗讲话”，科学出版社，1981年。）

1981b“重遇沈从文”，“海内外”，1981年第28期，第25-26页。重印于“大地”，第2期，第27-28页。

1981c“Some facts about Kurt Gödel”，Journal of Symbolic Logic 46，653-659. Reprinted with some revisions in［1987a］，Chapter 2.

1981d“Specker's mathematical work from 1949 to 1979”，L'enseignement mathématique 72，85-98.Also in Erwin Engeler，Hans Läuchli，and Volker Strassen（eds.），Logic and Algorithmic：An International Symposium Held in Honour of Ernst Specker，Zürich，February 5-11，1980，pp.11-24.

1981e“哥德尔和维特根斯坦”，“哲学研究”，1981年第3期，第25-37页。

1981f“数理逻辑”，“自然科学问题”，1981年第3期，第70-71页。

1982a“由鲁迅来印证几项感想”，“读书”，1982年第4期，第70-76页。

1982b“对金岳霖教授的回忆”，“广角镜”，1982年第122期，第61-63页。重印于：“中国哲学”，1984年第11期，第487-493页；“金岳霖的回忆和回忆金岳霖”，四川教育出版社，1995年，第161-167页。English translation，［2011a］.

1983“Philosophy：Chinese and Western”，Commentary：Journal of the National University of Singapore Society 6，No.1（September 1983），1-9.

1984a“The formal and the intuitive in the biological sciences”，Perspectives in Biology and Medicine 27，525-542.

1984b“Computer theorem proving and artificial intelligence”，Contemporary Mathematics 29，49-70.Reprinted in［1990a］.

1984c“Wittgenstein's and other mathematical philosophies”，The Monist 67，18-28.

1984d“Thought and action”，South China Morning Post，The Hong Kong Standard，June 1，1984.

1985aBeyond Analytic Philosophy.Doing Justice to What We Know.Cambridge，Mass.：MIT Press.Paperback edition，1987.（“超越分析哲学——尽显我们所知领域的本相”，浙江大学出版社，2010年。）

1985b“Two commandments of analytic empiricism”，Journal of Philosophy 82，449-462.Partly incorporated into［1985a］，Introduction.（“分析经验主义的两个戒条”，“中国社会科学”，1985年第4期。）

1986a“中国和西方哲学”，“中国文化”，1986年第1卷第1期，第39-60页。

1986b“Quine's logical ideas in historical perspective”，in Lewis Edwin Hahn and Paul Arthur Schilpp（eds.），The Philosophy of W.V.Quine，pp.623-643.La Salle，Ill.：Open Court.2d ed.1998.

1986c“哥德尔等人关于问题演变的一些例子”，“哲学译丛”，1986年第6期，第62-66页。

1987aReflections on Kurt Gödel.Cambridge，Mass.：The MIT Press.Paperback edition，1990.（“哥德尔”，康宏逵译，上海译文出版社，1997年。）

1987b“Gödel and Wittgenstein”，in Paul Weingartner and Gerhard Schurz（eds.），Logic，Philosophy of Science and Epistemology，pp.83-90.Proceedings of the 11th International Wittgenstein Symposium，Kirchberg amWechsel，Austria，4-13 August，1987.Vienna：Verlag Hölder-Pichler-Tempsky.

1987c“哥德尔的数学客观主义”，“北京大学学报”，1987年第1期。

1987d“Einstein and Gödel：Contrast and friendship”，Journal of Tsinghua University 2，No.1，32-39，56.Revised and enlarged version in Chinese，“Exploring the eternal：Gödel and Einstein”，Twenty-First Century Bimonthly，No.2（December 1990），72-81.（“探索永恒：哥德尔和爱因斯坦”，“二十一世纪双月刊”，1990年第2期，第72-81页）

1987e“金岳霖先生的道路”，载“金岳霖学术思想研究”，四川人民出版社，1995年。

1987fReviewofGalvanoDellaVolpe，LogicasaPositiveScience（Chinese）.Chinese Culture Quarterly 1，No.3（Spring 1987），101-104.Translated from English by Ser-min Shei.（“对加拉瓦诺·德拉·沃尔普《作为实证科学的逻辑学》的评论”，“九州学林”，1987年春季号第3卷第1期，第101-104页。）

1987gReview of David Rubenstein，Marx and Wittgenstein：Social Praxis and Social Explanation（Chinese）.Chinese Culture Quarterly 1，No.3（Spring 1987），104-107.Translated from English by Ser-min Shei.（“对大卫·鲁宾斯坦《马克思和维特根斯坦：社会实践和社会解释》的评论”，“九州学林”，1987年春季号第3卷第1期，第101-104页。）

1989a“Tharp and conceptual logic”，Synthese 81，141-152.

1990aComputation，Logic，Philosophy.A Collection of Essays.Beijing：Science Press.Dordrecht：Kluwer Academic Publishers.

1990b“Philosophy through mathematics and logic”，in Rudolf Haller and JohannesBrandl（eds.），Wittgenstein—TowardsaReevaluation，pp.142-154. Proceedings of the 14th International Wittgenstein Symposium，Centenary Celebration，KirchbergamWechsel，Austria，1989.Vienna：VerlagHölder-Pichler-Tempsky.

1990c“Mind，brain，machine”，Jahrbuch 1990 der Kurt-Gödel-Gesellschaft，5-43.Proceedings of the First Kurt Gödel Colloquium，Salzburg，Austria，September 1989.

1990d“Aperiodicityandconstraints”，Jahrbuch1990derKurt-Göodel-Gesellschaft，88-93.

1990e“在文学和哲学之间——读王友琴论鲁迅”，“读书”，1990年第4期，第58-66页。

1991a“Gödel's and some other examples of problem transmutation”，in T. Drucker（ed.），Perspectives on the History of Mathematical Logic，pp.101-109.Boston：Birkhäuser.Chinese translation，［1986c］.

1991b“Toandfromphilosophy—DiscussionswithGödelandWittgenstein”，Synthese 88，229-277.

1991c“Kurt Gödel et certaines de ses conceptions philosophiques：l'esprit，la matière，la machine et les mathématiques”，in G.Hahn and M.A.Sinaceur （eds.），Penser avec Aristote：Etudes réunies sous la direction de M.A. Sinaceur，pp.441-451.Toulouse：Erès.（［1979a］.）

1991d“Gödel and Einstein as companions”，in John Brockman（ed.），Doing Science：The Reality Club，pp.282-294.New York：Prentice Hall Press.

1993a“Imagined discussions with Gödel and with Wittgenstein”，Jahrbuch 1992 der Kurt-Gödel-Gesellschaft，pp.3-49.

1993b“身体或计算机有灵魂吗？（I）物理世界的精神物理学平行论和算法主义”，“二十一世纪双月刊”，1993年第15期，第102-110页。

1993c“身体或计算机有灵魂吗？（II）心灵的算法主义和可行性问题”，“二十一世纪双月刊”，1993年第16期，第72-78页。

1993d“On physicalism and algorithmism：Can machines think？”Philosophia Mathematica（III）1，97-138.

1993e“What is logic？”，in Klaus Puhl（ed.），Wittgenstein's Philosophy of Mathematics，pp.11-23.Proceedings of the 15th International Wittgenstein Symposium，part 2.Vienna：Verlag Hölder-Pichler-Tempsky.Also The Monist 77（1994），261-274.

1993f“从昆明到纽约”，“读书”，1993年第3期，第140-143页。English translation，［2011b］.

1993g“New Directions in Science and in Society：From Traditions to Innovations”，in Nineteenth World Congress of Philosophy，Moscow，August 1993，Book of Abstracts：Invited Lectures，pp.52-59.Moscow.

1995“Time in philosophy and in physics：From Kant and Einstein to Gödel”，Synthese 102，215-234.

1996aA Logical Journey：From Gödel to Philosophy.Cambridge，Mass.：MIT Press.（“逻辑之旅：从哥德尔到哲学”，邢滔滔等译，浙江大学出版社，2009年。）

1996b“Skolem and Gödel”，Nordic Journal of Philosophical Logic 1，119-132.

2005“Language and metaphysics”.Journal of Chinese Philosophy 32，No. 1，139-147.Translation by Richard Jandovitz and Montgomery Link of ［1945］.

2009（With Jens-Erik Fenstad.）“Thoralf Albert Skolem”.In Dov Gabbay and John Woods（eds.），Handbook of the History of Logic，volume 5：Logic from Russell to Church，pp.127-194.Amsterdam：North-Holland.

2011a“Memories related to Professor Yuelin Jin”.Translation by Montgomery Link and Richard Jandovitz of［1982b］.In Charles Parsons and MontgomeryLink（eds.），HaoWang，LogicianandPhilosopher，pp，27-38.London：College Publications.

2011b“From Kunming to New York”.Translation by Richard Jandovitz and Montgomery Link of［1993f］.In Parsons and Link，op.cit.，pp.39-45.

2011c“Sets and concepts，on the basis of discussions with Gödel”.Edited with introduction and notes by Charles Parsons.In Parsons and Link，op.cit.，pp.79-118.

2015-11-5

*We would like to express our heartfelt gratitude to Professor Xinwen Liu and Professor Sumin Xia for their help and support.