连续统问题与薄实在论

高坤

北京大学哲学系

gaokun_ps@163.com



连续统问题与薄实在论

高坤

北京大学哲学系

gaokun_ps@163.com

哥德尔对连续统问题的独立性的柏拉图主义回应作为一种“厚实在论”招致麦蒂（Penelope Maddy）的一个批评。作为一种可能的替代，麦蒂提出了所谓的“薄实在论”。本文试图论证麦蒂对厚实在论的批评并不像表面上看来那么有力，而薄实在论作为一种本体论立场涉嫌一种自相矛盾，并且后者也不能像厚实在论那样赋予连续统问题以客观意义。

连续统问题；哥德尔；麦蒂；柏拉图主义；薄实在论

1　引言

连续统问题（the Continuum Problem）作为一个关于实数子集大小的问题，首先是一个数学问题。但通行集合论公理在判定这个问题上的无力使得它衍生出一个相应的哲学问题，即连续统问题有没有意义的问题。对于这后一个，哲学意义上的“连续统问题”，数学哲学家们给出了各种不同的回答，其中尤以哥德尔（Kurt Gödel）所代表的柏拉图主义立场最为有影响。事实上，与此立场密切相关的所谓“哥德尔纲领”（Gödel's Program），在很大程度上塑造了当代集合论的实践。然而不可否认的是，柏拉图主义存在种种困难，最为人熟知的便是关于抽象对象的认识论问题，亦即贝纳塞拉夫问题。1因为是贝纳塞拉夫（Paul Benarcerraf）首先系统分析了抽象对象在认识论上可能引起的困难，参见［1］。对于这个问题，哥德尔本人并非没有注意到，相反他倾注了很多心血在数学认识论的探索上，例如他提出了一种数学直觉学说以期说明心灵对数学对象的把握，只是后者本身的内在合理性遭到学者们的普遍质疑。2参见本文第三节。

虽然如此，数学柏拉图主义作为推动当代集合论实践的重要力量，被很多人认为是与集合论实践符合得最好、反过来也为集合论实践所支持的哲学立场。3例如，在参考文献［12］中，郝兆宽等人论证了武丁（Hugh Woodin）在集合论上的一些重要工作与柏拉图主义的互相支持。对于这样一种近乎标准的看法，麦蒂（Penelope Maddy）提出了异议。通过具体地考察集合论在历史上和当代的实践，麦蒂试图论证柏拉图主义与集合论实践并不相符，反而有某种难以逾越的矛盾。4麦蒂这方面的工作可参阅文献［7，9，10］，其中尤以［10］最为详细。并且，作为对柏拉图主义这种“厚实在论”（Robust Realism）的一个可能替代品，麦蒂还提出了所谓的“薄实在论”（Thin Realism）5麦蒂虽然是薄实在论的主要阐述者，她对薄实在论的态度却是复杂的。她的基本哲学立场是作为自然主义的一种形式的“第二哲学”立场，参见文献［9］。在第二哲学下，麦蒂认为，薄实在论和与之相反的“非实在论”（Arealism）是同等合理的，并因而建议哲学家们取消关于数学的真理和存在问题的哲学讨论，将注意力转移到纯粹的方法论研究上去，参见文献［10］。对此本文第四节还会有说明。，并阐述了此立场下连续统问题的地位。那么，麦蒂对柏拉图主义的批评合理吗？她的薄实在论和她对哲学连续统问题的回答经得起理性的推敲吗？本文将对这些问题作深入的探讨。

首先，在本文第二节，本文将简单回顾连续统问题的提出和发展过程，阐述此问题如何成为一个哲学问题，并介绍哥德尔纲领的内容和它对当代集合论实践的影响。然后，在第三节，笔者将分析麦蒂对柏拉图主义的批评，试图表明，麦蒂的批评并不像表面上看来那么新颖，其归根结底还是要诉诸哥德尔数学直觉学说的内在困难。最后，在本文第四节，笔者考察薄实在论和它对连续统问题的态度，表明薄实在论涉嫌回避关于数学对象的本体论问题，即数学对象（如集合）是否具有客观实在性的问题，或者说，在这个问题上它采取了一种自相矛盾的立场。特别地，薄实在论对排中律的简单援引也无法回答作为一个哲学问题的连续统问题。

2　连续统问题与哥德尔纲领

作为数学问题的连续统问题由无穷集合论的创立者康托提出。康托用“一一对应”定义集合的大小，并证明无穷集合并不是一样大的。特别地，康托用他发明的对角线法证明，任何集合的幂集都严格地大于该集合本身。例如，实数集就严格大于自然数集，因为很容易证明，实数集和自然数集的幂集一样大。那么，是否存在实数集的一个子集，它严格小于实数集却又严格大于自然数集呢？这就是连续统问题，又称为“希尔伯特第一问题”，因为在20世纪初由著名数学家希尔伯特所提出的23个未解数学问题中，它位列第一。

康托猜想连续统问题的答案是否定的，即不存在实数的子集，其大小严格介于自然数集和实数集之间，这就是连续统假设（CH）。如果用基数6“基数”及本文涉及的其它集合论术语的技术定义可参阅文献［4］。表示集合的大小，并接受选择公理7选择公理使得任意两个集合可以比较大小，并使全体基数排成一个良序。，则CH可以用公式表达如下：

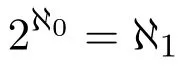
这里ℵ0是自然数集的基数，ℵ1是大于ℵ0的最小的基数。实数集的基数等于ℵ0的幂基数2ℵ0。另外，CH还可以推广为所谓的广义连续统假设（GCH），它断言任意无穷基数的幂基数恰好等于它的后继基数（即大于该基数的最小的基数）。

康托虽然相信CH是真的，但他并没有能证明它。在康托之后几十年间，证明或证否CH的诸多努力也都以失败告终，直到哥德尔和科恩（Paul Cohen）的工作表明，CH（以及更一般的GCH）“逻辑地独立于”数学家们普遍接受的集合论公理系统ZFC。在罗素分支类型论的启发下，哥德尔于1938年用可构成集构造了ZFC的一个模型L，并证明在L中CH是成立的。8证明思路是先证V=L（即一切集合都是可构成的）在L中成立，然后由V=L推出CH。这意味着CH对ZFC具有“相对一致性”，即如果ZFC是一致的，则ZFC+CH也是一致的。1963年，科恩又用他发明的力迫（forcing）法证明：如果ZFC是一致的，则ZFC+¬CH也是一致的。这样，综合哥德尔和科恩的结果我们知道，连续统问题超出现有数学的框架，不能由现有集合论公理判定。事实上，后续的一些工作表明，ZFC在约束无穷基数幂函数的行为上，能力非常有限。9这方面工作都得益于力迫法的巨大功效，文献［12］包含有这方面结果的一个简明介绍。

连续统问题的独立性结果引发了关于该问题地位的争论。形式主义者们，例如科恩，认为它表明连续统问题是没有意义的；柏拉图主义者们，如哥德尔，则坚信连续统问题有一个确定的答案，只是ZFC作为对集合宇宙的不完全描述，不足以解答它。如此一来，连续统问题在一定意义上就从一个纯数学问题演变成一个哲学问题，而哥德尔在这个问题上的柏拉图主义立场则与本文主题密切相关。

如上所述，哥德尔认为连续统问题是有意义的数学问题。为了解决它，哥德尔建议数学家们寻找新公理加强ZFC，使得加强后的公理系统能够判定CH的真假（以及其它独立性命题）。这就是所谓的“哥德尔纲领”（［12］，第33页）。哥德尔还探讨了寻找新公理应当遵循的原则，在《什么是康托的连续统问题？》一文中他写道：

…即使不考虑一个新公理的内在必然性，甚至即使它根本没有内在的必然性，以另一种方式，即通过归纳地研究它的“成功”，对其真值作出一种盖然的判定依然是可能的。这里成功意味后承的丰富性，特别是“可证实的”后承，即不借助新公理也能得到证明的后承，但新公理能使这些证明变得更简单和更容易发现，并使得将许多不同的证明归结为一个证明成为可能。…或许存在这样一些公理，它们的可验证的后承是如此丰富，它们对一个领域的阐释是如此清晰，它们提供的解决问题的方法是如此强大（甚至能最大限度地以构造性的方式解决它们），以至于无论它们自身是否是内在必然的，它们都必须被接受，至少在与任何良好建立的物理理论同样的意义上被接受。（［3］，第261页）

这里引人注意的是，哥德尔认为公理不必有直观上的显明性，只要具备其它一些优良的理论性质，如可验证后承的丰富性、对理论的简化作用等，就可以被接受为真。哥德尔纲领和他关于公理证成的如上原则，极大地影响着之后的集合论实践，正如郝兆宽（和施翔晖，杨跃一起）指出的，它们“几乎指导了所有寻求新公理的工作”（［12］，第35页）。最具代表性的一个例子是加州学派围绕投射可决定性公理（PD）的大量结果，对于它下一节我会再作介绍。

现在我们可以来概括一下哥德尔对连续统问题的立场：

1.本体论：集合等抽象对象（即不在时空中也不具有因果性）是独立于心灵的客观存在；

2.逻辑学：所以，连续统假设虽然独立于ZFC却仍然有确定的真值，或者CH或者¬CH；

3.方法论：应该寻找新公理以判定CH，新公理的证成可诉诸它所导致的数学理论的一些“好的性质”。

哥德尔的这一立场被称为是“厚实在论”的，招来了很多批评。但大部分批评直接指向其本体论论点，质疑抽象对象在认识上的可达性，而麦蒂在集合论方法论上的研究工作则将矛头指向了新的方面，即其本体论论点与方法论论点的一致性上。下面，我就转入对麦蒂的这方面观点的讨论。

3　麦蒂对厚实在论的批评

数学方法论问题，特别是集合论公理的证成问题，是麦蒂哲学的一个中心关怀。起初，她从一种与哥德尔柏拉图主义有密切亲缘关系的实在论立场10即麦蒂的“集合论实在论”，参见文献［5］。考虑这个问题。但不久，她就放弃了这种立场，转向一种数学自然主义，要求严格区分方法论问题和关于数学存在和数学真理性的哲学问题。造成这种转变的原因之一，就是麦蒂发现柏拉图主义与集合论的实践并不相容。为了说明这一点，我们来看一看麦蒂对作为实践的集合论的方法论刻画。麦蒂仔细考察了作为实践的集合论：康托和戴德金对集合的引入，策梅洛对他制订的集合论公理系统，特别是选择公理的辩护，以哥德尔为代表的集合论学家们对V=L的普遍拒斥，加州学派关于投射可决定性公理PD的工作，等等。11这些考察可参见文献［7］和［10］。这里限于篇幅和本文目的，我们仅对最后一个案例，即PD作更详细的介绍。

正如本文第二节提到的，连续统问题的独立性，以及随后被集合论学家们陆续证明的大量独立性结果（如投射集勒贝格可测性问题）推动集合论学家们寻找新的原则以判定这些问题，而围绕可决定性假设（Determinacy Hypotheses）的研究就是在这一背景下产生的。完整的可决定性公理12设A是0和1之间的一些实数（它们可以唯一地表示成0和1的无穷序列）构成的一个集合，两个游戏者甲和乙轮流选择0或1，如果最终得到的实数属于A，则甲胜出，否则乙胜出；如果甲和乙中一人有制胜策略，则称集合A是可决定的。此定义可推广到全体实数上，可决定性公理断言实数的任意子集都可决定。被表明与选择公理不相容，但断言实数的投射子集都可决定的PD，却被很多集合论学家认为是很有可能成立的。显然，PD本身并没有直观上的似真性或内在的必然性，因此支持它的都是外在的证据，麦蒂将这些证据概括为四类（［10］，第49-51页）：

（1）PD使我们得到一个关于投射集性质的很丰富的理论，并且它是以一种很自然的方式，将我们只用ZFC就能得到的关于低层谱投射集的理论，推广到完整的投射集层谱上去。

（2）PD显示出与大基数公理（Large Cardinal Axioms，简记为“LCA”）的紧密联系，特别地，由一些大基数公理可以推出PD。而大基数公理被普遍认为具有某种内在似真性，这种内在证据及大基数公理的其它外在证据可以由PD继承过来。

（3）任何具有足够强（至少和PD一样强）的一致性强度（consistencystrength）13由哥德尔第二不完全性定理，皮亚诺算数PA不能证明它自身的一致性，但ZFC却可以，在这个意义上，ZFC的一致性强度要高于PA。类似地，ZFC+LCA可以证明ZFC的一致性，因而在一致性强度上高于后者。的自然的数学理论都蕴含PD。而考虑到集合论的基础地位和现代数学的开放性，我们完全有理由寻求具有更高一致性强度的理论。

（4）在足够强的大基数公理下，PD所提供的投射集理论不仅能回答关于投射集的所有已知独立性问题，还在如下意义上是完全的14这被称为“脱殊完全性”（generic completeness）。：用力迫法无法得到任何新的独立性结果。而力迫法是我们目前拥有的证明独立性的最好方法。

不难看出，以上这些证据都体现了我们之前提到的哥德尔原则，即根据公理导致的数学理论的理论性质来对备选公理进行取舍。麦蒂自己则将这种方法论刻画为：“使用任何有助于满足我们的数学目标的手段”，这些目标包括“局部的问题解决、提供数学基础、带来更开放的有前景的新数学内容”等等。（［10］，第52页）

但一个数学理论具有数学家们偏爱的这样或那样的性质，满足数学家们的某种数学目的，为什么就能保证这个理论是真的呢？麦蒂质疑道。集合论学家们喜欢PD带来的关于投射集的完美理论，但如果柏拉图主义将集合论看做是对某种客观的、独立实在的描述，那么“实在完全可以是令人悲伤地拒绝合作的”（［10］，第58页），即它很可能不服从人类对理论的那些主观的偏好，就像我们在物理学实践中常常看到的、实在与科学家意愿相违背的情况一样。由此，麦蒂得出厚实在论与集合论实践不一致的结论，而又因为后者实际上体现了我们在第一节介绍的哥德尔的方法论论点，麦蒂的如上结论成立的话就意味着哥德尔的本体论论点与方法论论点不一致。

虽然我不是数学实在论者，反倒更倾向于数学唯名论立场，但我不得不承认麦蒂对实在论之缺陷的上述观察并不像表面上看起来那么有说服力。因为，考虑一下自然科学中的情况，我们会发现自然科学家们对科学理论的论证也不是直接论证理论的真理性，而是理论具有这样那样的优点，或者说后者是前者的理由，即我们相信理论的真理性正由于它们具有那些理论优点（theoretical virtue）。蒯因（W.V.O.Quine）对这些优点进行过一般性的概括（［11］）——简单性，保守性，经验恰当性（empirical adequacy），融贯性，经济性，多产性（fecundity），等等。如果按麦蒂对数学所做的那样思考科学确证，则人们完全可以批评说，一个科学理论具有那些蒯因式优点并不能保证它是真的，独立于我们的物理实在完全可以不配合我们对这些优点的偏好，例如它可能就是包含一些对我们说明观察到的自然现象不必要的实体或性质，因而科学实在论与科学的方法论实践不相容。然而，我们会愿意在自然科学的情形下接受这样的结论吗？我们会认为我们对物理对象实在性的信仰与我们的自然科学实践不符吗？当然不，至少对于自然主义者来说，答案是不。既然如此，为什么在数学的情形下我们就要得出麦蒂式结论呢？难道像哥德尔那样得出数学证成和物理证成相似的结论不是更合理吗？事实上哥德尔在为数学的那种证成原则做辩护时正是诉诸这样的类比，比如在前面第二节中的引文中他说“它们都必须被接受，至少在与任何良好建立的物理理论同样的意义上被接受”。

这里，也许有人会为麦蒂辩护说，以上的考虑依赖于蒯因关于科学确证（confirmation）的整体论，而麦蒂对蒯因整体论是有异议的。确实如此，但麦蒂对整体论的异议主要在于反对将理论优点作为存在性断言的最终证据，反对笼统地不加区分地看待科学断言和科学证据。比如以原子论为例，麦蒂认为后者对那些蒯因式理论品质的享有还不足以让科学家们相信原子的实在性，更直接的证据如佩林关于布朗运动的实验是必要的和最关键的。同样地，她反对蒯因凭借整体论做出的关于数学对象存在性的不可或缺性论证。15文献［8］包含麦蒂对蒯因的整体论和不可或缺性论证的异议的一个简要概括。至于一般地援引理论的整体性优点为自然科学理论辩护，她并不反对。

针对我提出的批驳，麦蒂自己更有可能采取的辩解是，“经验恰当性”这个理论品质可以在很大程度上削弱自然科学家们的主观理论偏好对理论的决定作用，因为它要求自然科学理论与经验观察相符，这实际上就是要求理论与实在相符。换句话说，在科学理论的众多理论品质中，经验恰当性不是人类的一个主观理论偏好，而是提供了一个客观性的源泉。并且很明显，经验恰当性在诸理论品质中占据着核心位置，一个理论无论多么简单和优美，如果它缺乏经验上的恰当性，与经验观察有很多不符，它就绝不能被科学家们接受。相反，一个理论如果在观察上十分成功，那么即使它在其它品质上有瑕疵，甚至是内在不融贯的，也会被科学家们接受，比如现代物理学中的两颗明珠——广义相对论和量子力学，它们之间有着一种深刻的矛盾，至今仍然困扰着理论物理学家们，但它们在观察上的惊人成功却使科学家们普遍地接受它们。这样，凭借经验恰当性这个品质，也许就可以避免在自然科学的领域做出类似于数学领域的麦蒂式结论。

对于麦蒂可能做出的以上辩解，我要指出的是，哥德尔实在论数学哲学中所包含的直觉恰当性要求也可以充当类似的角色，它要求那些自身缺乏直觉显明性的数学公理，必须在其逻辑后承上与人们相关的数学直觉保持一致，比如集合论公理的算术结果应当与我们对标准自然数模型的直觉一致。事实上，哥德尔自己经常将数学直觉和它在数学中的作用类比于感官知觉和它在物理学中的作用16哥德尔的这方面论述主要参见［2］和［3］。，比如在他1964年的文章《什么是康托的连续统问题？》中他说：

但是，尽管它们离我们的感官经验极为遥远，我们对集合论的对象仍然有某种类似于知觉的东西，这由如下事实可以看出，即公理迫使我们接受其为真。我看不到任何理由使得我们对这种知觉，即数学直觉比对感官知觉怀有较少的信心，后者引导我们建立物理理论，预期未来的感官知觉会与这些理论相符，并相信一个现在不能判定的问题有意义并可能会在将来得到判定。（［3］，第268页）

当然，麦蒂对此还可以反驳说，哥德尔的数学直觉理论很不充分，很难期望数学直觉在数学认识中能具有与感性知觉在物理学中具有的相类似的性质和功能。但这样一来，麦蒂对哥德尔实在论的批评就归结为对哥德尔数学直觉学说的批评，失去其新颖性，因为后一种批评早已是老生常谈，其背后隐藏的则是关于数学实在论的贝纳塞拉夫难题。

4　薄实在论及其立场下的连续统问题

在上一节我们看到，麦蒂认为厚实在论与集合论实践不相协调，因而拒斥厚实在论。但这里应当注意的是，导致麦蒂拒斥厚实在论的原因并不仅有这一个，更深刻的原因在于她不接受关于数学对象实在性的不可或缺性论证，后者在她看来与自然科学实践不符。（［6］）不过对此我不打算作更多的探讨，那已超出本文的范围。我们更关心的是，在拒斥了厚实在论后，关于数学的本性以及特别地，关于连续统问题的地位，应该采取什么样的立场。麦蒂认为，其中一种可能的立场就是薄实在论。

根据麦蒂，薄实在论是这样一种观点，它认为集合存在，集合论是一些真理的总体（a body of truth），并且“集合就是集合论所描述的东西”（［10］，第63页）。因为集合论从未谈及集合的时空和因果性质，所以可以将非时空性、非因果性等否定性质归给集合。但关于集合的正面性质，薄实在论只接受集合论里所断言的那些，而拒绝作更多的形而上学探究。厚实在论试图为集合论方法的可靠性提供一个非平凡的说明，薄实在论则将之看作是“关于集合之所是的平凡事实”（［10］），既然集合就是集合论所描述的东西，集合论方法当然可以认识它们，因而关于集合的认识论难题和麦蒂所提出的集合论方法与集合的客观实在性之间的矛盾都消失了。特别地，麦蒂以连续统问题为例说明两种实在论的区别，在这个问题上，厚实在论想要一个“能够以更实质性的方式保证CH有意义的完整的形而上学理论”（［10］，第64页），而薄实在论则通过对排中律的简单援引来说明CH的有意义性，至于为什么可以使用排中律，则仅仅是因为它包含在集合论实践事实上所蕴含的方法中。

麦蒂声称伯杰斯（John P.Burgess）和斯蒂尔（John Steel）是上述薄实在论观点的两个代表（［9］，第368页），而她自己对薄实在论的态度则更复杂。麦蒂的基本哲学立场是自然主义的，在这种立场下，麦蒂认为薄实在论和非实在论（Arealism）是对数学实践的同等恰当的描述。这里的非实在论是和薄实在论相反的一种观点，它断言集合不存在，集合论不是一些真理的总体。某种程度上，非实在论可看作数学唯名论的一种形式，但与一般形式的唯名论不同的是，它不要求重新解释数学陈述和改变数学实践，在方法论层面上它与薄实在论无异。麦蒂关于薄实在论与非实在论同等合理的奇怪论点，本文不拟作更多的讨论，我们仅专注于薄实在论。

关于薄实在论首先要考问的一个问题是，当它断言集合存在时是否是断言集合的客观实在性？答案似乎应当是肯定的。很难设想麦蒂可以作出某种类似于卡尔纳普的框架内和框架外问题区分的区分，因为她是一个自然主义者，并明确承认她是在自然科学中就存在和真理等哲学问题发问。17例如，在文献［8］中麦蒂将自己的自然主义与伯杰斯的自然主义进行比较时，她着重强调这一点。对她来说，断言集合存在就像断言原子存在一样，是断言相关对象的客观实在性。然而薄实在论又宣称，集合就是集合论所描述的东西，这似乎又暗示集合是集合论方法所构造的，而非客观实在的对象。因为假如集合是客观实在的，它就不会天然地配合集合论方法，正如麦蒂自己在批评厚实在论时所指出的那样，集合论方法的可靠性就需要进一步的说明，不能武断论定集合就是集合论所描述的东西，正如不能武断论定原子就是原子物理学所描述的东西。这样看来，薄实在论就涉嫌一种自相矛盾的立场。薄实在论的动机是回避贝纳塞拉夫难题，通过断言集合就是集合论所描述的东西，使集合论方法的可靠性成为关于集合之所是的平凡事实。但这样做的代价是使集合成为某种不具有客观实在性的东西，使实在论成为非实在论。

关于薄实在论的第二个问题是，它能赋予连续统问题以客观的数学意义吗？根据薄实在论，无需借助集合的形而上学性质来为连续统问题的有意义性做保证，对排中律的简单援引就足够了。根据排中律，要么CH成立，要么¬CH成立，因而连续统问题就有一个确定的真值。对于排中律的这种应用，哥德尔当然也会同意，但在哥德尔看来，排中律之所以可以这样应用，正是因为数学对象的客观实在性，如果数学是心灵的创造，比如根据直觉主义，存在即在直觉中被构造，排中律的应用就在很多情况下是不合法的，这也导致直觉主义提出所谓“直觉主义逻辑”作为对数学中的古典逻辑的替代。当然，薄实在论虽拒绝诉诸集合的形而上学性质为排中律辩护，但也为排中律的可应用性提供了自己的理由：排中律是集合论和更一般的经典数学方法的一部分，麦蒂所坚持的数学自然主义亦即数学在方法论上的自主性就保证了它的合法性。对于麦蒂的这样一种观点，我有如下两个层次上的反驳。

首先，麦蒂必须说明连续统假设与其它一些特别的数学命题如几何学中的平行公设的区别。显而易见，在几何推理中我们也使用排中律和它衍生的反证法，但现在却没有哪个数学家会因此认为平行公设具有唯一确定的真值，相反人们一致同意，它仅在欧氏几何中成立，在非欧几何中则不成立。那么为何连续统假设就不能在一种集合论中成立，在另一种集合论中不成立呢？对此，麦蒂也许会说，这是因为集合论与几何学具有不同的数学地位。集合论是全部数学的基础，集合是比其他数学对象更真实的数学对象，因为其他一切数学对象如几何学的对象可以由集合构造出来。在这个意义上，集合论是我们的元数学，各种几何学则是我们在元数学里探讨的对象数学，它们在元数学所提供的一种模型中是真的，在另一种模型中则是假的。总之，集合论的数学基础角色决定了连续统假设在性质上和平行公设不同，它可以从排中律得到唯一确定的真值的保证，我们可以有多种不同的几何学，却只能有一个集合论。然而，对于麦蒂这种可能的回应，我们还可以这样来答复：至少对于现有数学而言，充当数学基础角色的仅仅是ZFC下的集合论，而连续统假设却独立于ZFC的公理，即使我们接受ZFC的绝对地位，将其作为我们的“绝对集合论”，又有什么理由阻止我们在它之外或者说之上使集合论分叉呢？事实上，当代集合论学家中提倡多宇宙集合论的形式主义者们，正是主张在ZFC判定范围以外放弃数学命题具有唯一确定的真值的柏拉图式想法的。在这种意义上，我认为，麦蒂薄实在论对排中律的简单援引并不能如数学柏拉图主义一样赋予连续统假设以唯一确定的真值，至少麦蒂必须说明，连续统假设究竟在何种深刻的意义上与平行公设不同，从而应当得到不同于我们对平行公设的对待。

其次，我们还可以对两种来源的排中律的力量作一个更一般意义上的分析。在柏拉图主义下，由于集合的客观实在性，排中律意味着对任意的集合论命题φ，都有φ为真或¬φ为真，但从数学实践所蕴含的方法论而来的排中律能有这种力量吗？我认为不能。在我看来，排中律作为数学方法论的合法成员，仅仅意味着我们的集合理论包含任意形如“φ∨¬φ”的集合论命题（在相应语言下的），并且因而反证法可以在集合论证明中应用，但它却不能保证我们的数学理论必然包含φ或¬φ。用数理逻辑为我们提供的概念来表达，我的看法是，集合论方法所决定的理论等效于｛φ|Γ⊢φ｝（即Th（Γ）），而集合的客观宇宙所决定的理论等效于｛φ|A|=φ｝（即Th（A）），这里Γ是集合论的公理集（如ZFC或它的扩张），A则表示那个客观的集合宇宙（假如它存在的话）。对于任意的集合论命题φ，都有A|=φ或A/|=φ，但根据哥德尔第一不完全性定理，却并非都有Γ⊢φ或Γ/⊢φ，虽然我们可以按照前文介绍的、主要由哥德尔和麦蒂所描述的那些方法论原则不断地寻找新的公理来加强Γ。

薄实在论试图避免厚实在论的困难，特别是集合论方法的可靠性问题，但由以上的分析可以看出，它既无法在保证自身一致性的前提下做到这一点，也无法像厚实在论那样赋予连续统问题以客观意义。因而它对于厚实在论的优越性很值得怀疑。然而也许应当表明的是，我虽然对薄实在论有种种异议，在此却不是要为厚实在论辩护，那是另外一个问题。

［1］ P.Benacerraf，1983，“Mathematical truth”，in P.Benaceraf and H.Putnam（eds.），PhilosophyofMathematics（2ndedition），pp.403-420，Cambridge：CambridgeUniversity Press.

［2］ K.Gödel，1995，“Is mathematics syntax of language？”，in S.Feferman（ed.），Kurt Gödel's Collected Works：Volume III，pp.334-356，Oxford：Oxford University Press.

［3］ K.Gödel，1995，“What is Cantor's continuum problem？”，in S.Feferman（ed.），Kurt Gödel's Collected Works：Volume II，pp.254-270，Oxford：Oxford University Press.

［4］ T.Jech，2003，Set Theory：The Third Millennium Edition，Revised and Expanded，Heidelberg：Springer-Verlag Press.

［5］ P.Maddy，1990，Realism in Mathematics，Oxford：Oxford University Press.

［6］ P.Maddy，1992，“Indispensability and practice”，Journal of Philosophy，89：275-289.

［7］ P.Maddy，1997，Naturalism in Mathematics，Oxford：Oxford University Press.

［8］ P.Maddy，2005，“Three forms of naturalism”，in S.Shapiro（ed.），Oxford Handbook of Philosophy of Mathematics and Logic，pp.437-459，Oxford University Press.

［9］ P.Maddy，2007，Second Philosophy：A Naturalistic Method，Oxford：Oxford University Press.

［10］ P.Maddy，2011，Defending the Axioms：On the Philosophical Foundations of Set Theory，Oxford：Oxford University Press.

［11］ W.V.Quine，1976，“Posits and reality”，The Ways of Paradox（Revised and Enlarged Edition），pp.246-254，Harvard University Press.

［12］ 郝兆宽，施翔晖，杨跃，“连续统问题与Ω猜想”，逻辑学研究，2010年第4卷第4期，第30-43页。

（责任编辑：崔建英）

Abstract

KurtGödel'sPlatonicreactiontotheindependenceofthecontinuumproblemincurs a criticism from Penelope Maddy.As a possible replacement，Maddy proposes the socalled“ThinRealism”.Inthispaper，thewritertriestoarguethatMaddy'scriticismisnot so powerful as it seems，and Thin Realism as an ontological stance，can be suspected of containing a kind of self-inconsistency.And particularly，Thin Realism cannot provide the continuum problem an objective sense as Robust Realism does.

The Continuum Problem and Thin Realism

Kun Gao
Department of Philosophy，Peking University
gaokun_ps@163.com

B81

A

2015-04-23；

2015-09-09