高中数学教学中培养学生形成数形结合思想的初步探讨

唐洁

【摘 要】分析高中数学数形结合思想研究的意义，阐明进行数形结合思想培养中常见的问题，阐述高中数学教学中培养学生数形结合思想的途径。

【关键词】高中数学 数形结合 教学途径

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2016）07B-0145-03

数学源于生活，用于生活。自诞生起，数学在人们的生活中占据重要的地位，也是其他学科如生物学、化学、物理学等学科的基础。数学思想一直为数学研究学者所重视，从17世纪的数学变换思想到18世纪的数学分析思想，再到19世纪的数学思想大变革，数学思想的研究从未停止过，尤其是20世纪以后有关数学思想的研究的论文与著作层出不穷。我国自1978年之后不断发展教育事业，对数学思想的研究也更加重视。据教育部的统计，近40年来我国数学思想的研究与应用主要集中在高中教学中。高中生已经有了一定的数学基础知识，并且处于数学思维和思想形成的有利年龄段。

随着我国教育事业近年来的飞速发展，数学教学的课程改革也在如火如荼地进行着，新课标要求数学教学过程中要加强数学方法的渗透，因为只有有了正确的思想方法，学生才能够合理地运用数学知识。四大数学思想方法为数形结合、化归、函数与方程以及分类讨论，而在高中教学中最为重要的就是数形结合，因为在一定程度来说其他三种思想的培养都涉及数形结合思想。数形结合思想贯穿于所有的数学研究与教学之中，是抽象概念与直观几何的有机结合。数形结合思想在高中教学中占据重要的位置，它不仅能简化各种数学问题的解决方法，而且能培养学生的数学思维。目前，我国高中数学教育中很多教学工作者对数形结合思想的重要性认识不清楚，导致高中数学数形结合思想培养中存在诸多问题，影响着高中数学教学工作的进展，同时也阻碍了高中生数学思维的发展。对高中数学教学过程中数形结合思想培养的途径进行探索，有着重要现实意义。

一、高中数学数形结合思想研究的意义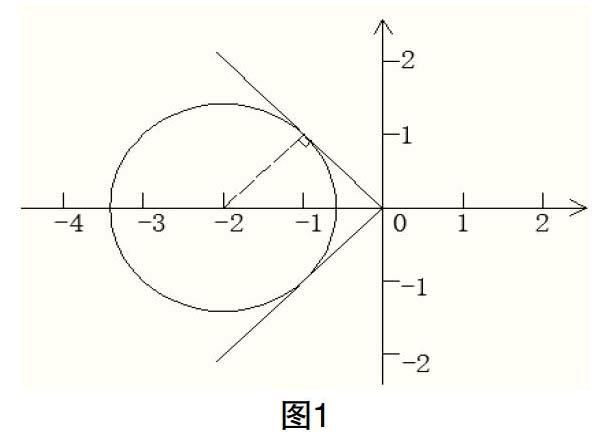

（一）有利于数学知识的过渡和衔接

在高中以前学生学习的都是较为基础的数学知识，知识点简单直观，例如初中教程中的不等式、方程以及几何中的三角形、多边形和圆等知识都较为简单，学生只用记住相关的概念以及公式就能够很好地解决常见的问题。但是高中的数学知识比较抽象，例如常见的函数、数列、圆锥曲线以及空间立体几何等都不可能与初中直观的知识同日而语。在高中数学每个知识点中基本上都会涉及数学理论与几何图形的结合，也只有这样才能够很好地让学生掌握所学内容。数形结合思想主要是为了学生能够合理地将数学逻辑理论与学生所学的各种几何图形相结合，以有利于数学知识的过渡和衔接。

（二）简化解题步骤节约解题时间

数形结合思想的培养不仅仅可以帮助学生快速地理解和掌握高中数学各知识点的概念和含义，而且还可以利用图形来解决一些函数求极值、方程求解、不等式求解以及立体几何与空间几何中的求值问题，使得这些问题的解决更加简单、直观。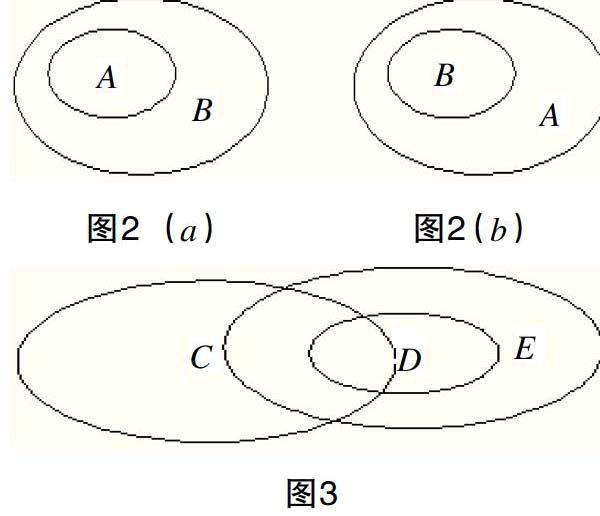

例如，已知（x+2）2+y2=2，求解如果此题采用常规的数学思路来解，一般先求x和y的值，需要用x来表示y，然后再求的最大和最小值。该方法显然比较麻烦，对于高中生来说一般很难求出其解或者容易出现错误。但是如果看出（x+2）2+y2=2是以（-2，0）为圆心，为半径的圆，且将看成是直线y=kx的斜率，就很容易求出其解。如图1，直接画出该函数所表达的圆与y=kx所表达的直线，则可以看出直线与圆相切时取最大和最小值，分别为1和-1。可见，运用数形结合有利于简化解题步骤，节约解题时间。

（三）培养高中生数学兴趣和数学思维能力

高中数学一直是许多高中生的“噩梦”，主要原因在于高中数学的知识点多、逻辑关系复杂、定义理解及掌握困难，而且在物理学和化学中又被广泛应用。许多学生因此患上了数学恐惧症，但是数形结合思想可以使得数学与生活实际结合起来，使得一些抽象的知识具体化，从而变得形象生动，提高学生的数学兴趣。应用数形结合的方法与思想，也可以大大降低一些解题难度，使得数学解题看起来更轻松，降低了学生对数学的恐惧，进而使得学生逐渐喜欢上这门课程。数形结合思想的培养可以培养学生的形象思维、逆向思维以及发散性思维，对学生后期的各科学习有着重要的意义。

二、进行数形结合思想培养中常见的问题

（一）数学教学中对学生数学思想培养不重视

不少高中生反映，学习数学枯燥乏味。这主要原因，归结于数学教学中对学生数学思想的培养不重视。据2014年，陕西省汉中市教育局对所属高中进行的一场调研显示，该市所属的高中有近80%的学生反映数学老师在教学过程中未曾提到过数学思想这一概念，这些学生连基本的四大数学思想方法都不知道，而其余20%的学校虽然在教学过程中有提到利用图形来解决一些问题的方法，但都是很简单地一笔带过，未给学生做仔细的讲解分析。教育工作者不重视学生数学思想的培养，从某种程度上来说，是对教学工作的不负责，也是对学生的不负责。这样做，不仅不利于学生知识的获取，而且在某种程度上还会加剧学生对数学学习产生厌恶感。

（二）数学教学中理论知识与生活实际结合不紧密

数学本来就是源于生活，最后回归到生活实际中去。但是，由于各种各样的原因，追求高成绩已经成为高中教育普遍的一种现象，教育工作者只在乎学生的成绩，而不注重学生思想、思维能力以及生活能力的培养。数学教学与实际生活相脱离，使得数学失去了其应有的价值。也就是说，如果在数形结合思想的培养过程中失去了“形”，那么要想培养学生形成数形结合思想就是天方夜谭。与实际相脱离，会使得学生对数学学习重要性认识不到位，降低学生学习的积极性，并且会导致学生思维更加局限，在某种程度上使得数学成为一种概念，而不能运用到实际生活中。数形结合思想也就成为空谈。

（三）数学教学中忽视学生之间数学思维的差异性

数形结合思想的培养是一个长期过程，该思想的培养要求学生，只有不断挖掘自己的思维能力，不断地进行相应的训练，才能逐渐地形成数形结合思想，并用之来解题，形成一种思维习惯。在学生刚进入高中的时候，教育工作者就要做好此方面的准备。虽然说对待学生要一视同仁，但是在入校时候每个学生的思维能力都不尽相同，有的学生接受能力较强，有的学生接受能力弱，需要一定的时间来适应。可是，在高中数学教学中很少有老师会注意到这一点。教师只按照自己的安排进行教学，忽视了学生是否已经有了数形结合的思想。在教学中也不注意了解学生的情况，不知道能否合理地应用数形结合思想来教学，于是就出现了高中生中常见的成绩好的越来越好，成绩差的无论怎么努力都鲜有提高，使得学生的数学思想教育得不到全面提升。

三、高中数学教学中培养学生数形结合思想的途径

（一）在教学过程中高度重视，不断渗透数形结合思想

作为数学教学工作者，在学生进入高中的那一刻起，就要有意识地对学生进行数学思想的培养。一方面，高中数学教学工作组要制定相关的教学制度，让每个数学老师制订各个年级教学过程中有关数形结合思想培养的教学计划，并落实到实处。另外一方面，教师要让学生认识到初中所学的理论知识以及几何知识都是为高中数学学习打基础，要让学生了解到理论知识与几何知识能够很好地结合，在二者的结合过程中所要用到的就是数形结合思想。在高中课程的各个章节中，基本上都能用数形结合思想来解决其中的问题。教师每教授一个新知识点时，要注意渗透该思想方法，让学生认识到这种方法的简便性、实用性、准确性，并能适用于解决哪类问题。如果教师在平时的数学教学中能不断地渗透数形结合思想，那么教师和学生就会越来越重视这种方法的培养与应用。

（二）要求学生学会用数形结合方法解题

学生对数形结合思想方法还不熟悉的时候，在进行数学问题解答时会习惯地用定式思维解题，因此，教师给学生布置练习题时要指定一些题目用数形结合的方法来解，这样可以逐渐地培养学生形成利用数形结合思想来解决问题的思维习惯。当学生利用数形结合方法解题时，要让学生将问题与实际生活结合起来。例如在进行函数问题求解时，注意把它与几何图形结合起来，把函数与图形相互融合，最终养成利用数形结合解题的习惯。

（三）重视学生思维的差异性，进行“形”与“数”之间的转化能力培养

在培养学生的数形结合思想的过程中，要重视学生思维的差异性。有的学生能够很好地进行“数”到“形”的转化，但是对“形”到“数”的转化却把握不准；有的却反过来，能较好地进行“形”到“数”的转化，却不能把握“数”到“形”的转化；有的学生却是二者之间的转换都存在问题。教师在教学过程中要通过平时作业来发现学生中思维能力的差异性，根据学生的差异制订相应的教学计划，以达到缩小学生之间思维差距的目的。

例如，集合A={2，4}，B={1，2，4，6}，问图2的（a）（b）中哪个反映出A与B的关系。之后再给出图3，让学生进行C、D、E等集合之间的关系判断。这样有层次性地训练，就能较好地照顾到不同层次学生之间的差异性，更好地培养学生的数形结合思想。

进行数形结合相互转化的讲解时，不仅要讲，而且要练。只有这样才能更好地培养学生的数形结合思想。

（四）在数形结合教学过程中让学生能够充分掌握图形工具

数形结合思想方法应用的基本的工具之一就是图形。教师在教授过程中要注意对一些特定的数学符号、公式与图形间的结合，例如将绝对值与数轴图形结合、正余弦与单位元结合、二次函数求解待定系数与二次函数图形结合、求解最小值时与两点间直线最短结合等。

例如，m+n=3（a，b>0），求的最小值。此题可将和分别看作是以m和1为直角边的三角形的斜边与以n和3为直角边的三角形斜边之和。根据初中几何知识由图4可得当B、C、D在同一直线上时有最小值5。

数学教学工作者要训练学生熟练使用各种图形工具，通过二维图形和三维立体图形形象地表达出各知识点数形结合的动态过程，有意识地培养学生的动态思维以及空间想象思维。

能力的提高在于思想的培养。高中数学只有抓紧数学思想的培养，才能从根本上提高数学的教学水平。在教学过程中，高中数学教师要不断地给学生灌输数形结合及其他数学思想方法，通过指定题目，使数形结合的教学得到落实。培养学生“形”与“数”之间的转化能力，为学生学好数学打下坚实的基础。

【参考文献】

[1]宫凡玉.高中数学教学中渗透数形结合思想的研究[D]鲁东大学，2015

[2]姜秋亚.数形结合思想方法在高中教学中的应用情况研究[D].华中师范大学，2015

[3]刘桂玲.数形结合思想方法在高中数学教学中的应用分析[J].中国校外教育，2015（13）

[4]杨颖.高中数学教学中数形结合法的运用探讨[J].品牌，2014（10）

（责编 卢建龙）