二阶半环生成的簇

张　可,任苗苗,邵　勇

(西北大学 数学学院,陕西 西安　710127)



·数理科学·

二阶半环生成的簇

张可,任苗苗,邵勇

(西北大学 数学学院,陕西 西安710127)

该文研究一些二阶半环生成的簇，先分别解决了这些簇的字问题, 进而证明这些簇是有限基底的, 并且给出了这些簇的方程基底。 然后, 解决了由所有这些二阶半环所生成的簇的字问题, 进一步, 给出了此簇的方程基底。

半环; 等式; 基底; 簇

设K是一个代数类。若K对子代数, 任意直积和同态像封闭, 则称其为簇。由Birkhoff定理知一个代数类是簇当且仅当它是满足某个等式集的代数的全体。设V是簇,如果存在V满足的一个有限等式集Σ使得V满足的每一个等式可由Σ演绎, 则称V是有限基底的(简称FB)。否则, 称V是非有限基底的(简称NFB)。设A是代数。若A生成的簇HSP(A)是FB[NFB],则称A是FB[NFB]。例如,每一个二元素的代数,有限的群,有限的环, 有限的格, 可换半群都是FB。第一个NFB的有限半群的例子是由Perkins在文献[1]中给出的。Dolinka在文献[2]给出了第一个有限的NFB半环的例子。

设(S,+,·)是(2,2)-型代数。若S满足下列条件:

1)(S,+)是可换半群;

2)(S,·)是半群;

3)∀a,b,c∈S) a·(b+c)=a·b+a·c,(b+c)·a=b·a+c·a，

则称(S,+,·)是半环。易见,半环的全体作成一个簇,记为SR。设X是一个可数无限集,X+是X上的自由半群,X*是X上的自由含幺半群。显然,可将半环等式记作如下形式u≈v,其中

u=u1+u2+…+uk,

v=v1+v2+…+vl,ui,

vj∈X+,1≤i≤k;1≤j≤l。

设S是半环。若对于任意的代换φ:X→S,φ(u)=φ(v),则称S满足u≈v,记为Su≈v。

许多学者对半环进了研究[2-13]。文献[10]引入了半群的闭子半群的概念，进而给出了所有乘法半群是带, 加法半群是半格的半环作成的簇的自由对象的模型。其后,文献[3, 5-6]证明了上述簇的子簇格是分配格,且有78个元素,此外,每一个子簇都是有限基底的,并且是有限生成的。文献[10]证明所有加法半群是半格的二阶半环生成的簇有64个子簇,且每个子簇都是有限基底的。Shao和Ren证明了由二元素分配格和三元素环生成的簇是有限基底的[9]。本文研究一些二阶半环生成的簇。解决了这些簇的字问题,并且证明这些簇是有限基底的,进一步,给出了这些簇的基底。

1　预备知识

为了解决由二阶半环生成的簇的字问题,我们引入以下概念。设u∈X+,则

·称u中出现的全体为u的容量,记作c(u);

·称第一个在u中出现的变量为u的首字母,记作h(u);

·称最后一个在u中出现的变量为u的尾字母,记作t(u);

·称出现在u中的所有变量的个数为u的长度(重复出现的变量也计数), 记作l(u)。

设u=u1+u2+…+uk，则

·集合∪{c(ui)| i=1,2,…,k}为u的容量,记作C(u);

·集合∪{h(ui)| i=1,2,…,k}为u的首部,记作H(u);

·集合∪{t(ui)| i=1,2,…,k}为u的尾部,记作T(u)。

设u=x+xyz+zty+sxyx+x，则

C(u)={x,y,z,s},H(u)={x,z,s},

T(u)={x,y,z}。

以下给出一些二阶半环的运算表和基底。其中,L1,R2,M2,D2,N2,T2的基底在文献[10]中已给出,Z1,Z2的基底将在下文中给出。

文中没有给出的概念和符号可以参考文献[14-15]。

2　主要结果

引理1设u≈v是非平凡半环等式, 其中

u=u1+u2+…+uk,v=v1+v2+…+vl,

ui,vj∈X+,1≤i≤k;1≤j≤l,则

1)L2u≈v当且仅当H(u)=H(v);

2)R2u≈v当且仅当T(u)=T(v);

3)M2u≈v当且仅当C(u)=C(v);

4)D2u≈v当且仅当

(∀ui∈u,vj∈v)(∃up∈u,vq∈v)

c(vq)⊆c(ui),c(vp)⊆c(uj);

5)N2u≈v当且仅当{ui∈u| l(ui)=1}={vj∈v| l(vj)=1};

6)T2u≈v当且仅当

{ui∈u| l(ui)≥2}≠∅,

{vj∈v| l(vj)≥2}≠∅；

7)Z1u≈v当且仅当

(∀x∈X) u≠x, v≠x;

8)Z2u≈v当且仅当m=n=1且C(u1)=C(v1),或m,n≥2。

表1　运算表

证 明1)-6)的证明参见文献[7,10]。

7)的证明 (⟹)Z1u≈v。不妨假设存在x∈X,使得u=x,v≠x。取x为1,其余变量为0,则有1=0,矛盾。对偶地,可以得到对于任意的x∈X,u≠x,v≠x。

(⟸)设∀x∈X,u≠x,v≠x。则∀φ: X→Z1,有φ(u)=φ(v)=0。因此Z1u≈v。

8)的证明(⟹)设Z2u≈v,假设m=1,n≥2,取所有变量都为1,则有1=0,矛盾。由对偶原理可得m=n=1或m,n≥2,当m=n=1时,由于(Z2,·)是半格,故C(u)=C(v)。

(⟸)当m=n=1且C(u)=C(v)时,由于(Z2,·)是半格,从而有

Z2u≈v。

当m,n≥2时,由于(Z2,+)是零半群,故

Z2u≈v。

设Σ是一个半环等式集。 以下将由Σ确定的半环簇记为[Σ]。

定理1

设S2=HSP(Z1)∨HSP(Z2),则

1)HSP(Z1)=[x+y≈z+t,xy≈x+y];

2)HSP(Z2)=[x+y≈z+t,xy≈yx,x2≈x];

3) S2=[x+y≈z+t,xy≈yx,x2y=xy];

证 明1)容易验证Z1x+y≈z+t，xy≈x+y]。从而HSP(Z1)⊆[x+y≈z+t,xy≈x+y]。以下只需证明Z1满足的每一个等式可由x+y≈z+t, xy≈x+y和SR的基底演绎。设Z1=u≈v，其中

u,v≠x, x∈X。由等式xy≈x+y可将u和v演绎为有限个变量的和。再利用等式x+y≈z+t可将左右两边是有限个变量的和的等式演绎为平凡等式。

2)容易验证Z2可以演绎出等式

x+y≈z+t, xy≈yx, x2≈x。

设Z2u≈v,由引理1结论7)知只需讨论下列两种情况:

·m, n≥2。则由等式x+y≈z+t有

u=u1+u2+…+um≈v1+v2+…+vn=v。

故HSP(Z2)是由等式x+y≈z+t,xy≈yx,x2≈x所决定的。

3)容易验证B2x+y≈z+t,xy≈yx,x2y≈xy。

设B2u≈v。只需讨论下面两种种情况:

当m, n≥2。则由等式x+y≈z+t有

u=u1+u2+…+um≈v1+v2+…+vn=v。故S2是由等式x+y≈z+t,xy≈yx,x2≈x所决定的。

定理2

设B8=HSP(L2, R2, M2, D2, N2, T2, Z1, Z2)。则B8是由等式(1)～(9)确定的半环簇

x2y≈xy;

(1)

xy2≈xy;

(2)

xyzt≈xzyt;

(3)

x+yz≈x+yz+xz;

(4)

x+yz≈x+yz+yx;

(5)

x+yz≈x+yz+x2;

(6)

x+yz≈x+yz+xyz;

(7)

x+yz≈x+yz+yzx;

(8)

x+y≈x+y+y;

(9)

证 明容易验证,B8满足等式 (1)～(9)。以下只需证明B8满足的每一个等式都可由等式(1)～(9)和SR的基底演绎。设B8u≈v,其中u=u1+u2+…+uk,v=v1+v2+…+vg,ui,vj∈X+,1≤i≤k;1≤j≤g,只需讨论下列两种情况。

·m=n=1且C(u)=C(v)。由于L2，R2，T2u≈v,所以H(u)=H(v), T(u)=T(v), l(u)≥2, l(v)≥2。从而由等式(1)～(3)可推出u≈v。

·m, n≥2。由等式(9)可将u≈v演绎为u≈u+vj, 1≤i≤k, v≈v+ui, 1≤j≤g。另一方面, 由以上k+g个等式可以得到u≈u+v≈v,故以下仅需要考虑如下形式的等式：u≈u+p,其中u=u1+u2+…+um, ui, p∈X+, 1≤i≤m, m≥2。分以下两种情形:

1) l(p)=1。由N2u≈u+p可知，存在ui∈u，使得ui=p，从而由等式(9)和SR的基底可推出u=u+p。

2) l(p)≥2。设p=x1… xl, l≥2。

由L2，R2u≈u+p,

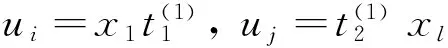
由M2u+p≈u可推出存在,其中。由D2u+p≈u可推出:存在us∈u使得c(us)⊆c(p)。由T2u+p≈u可推出存在uf∈u使得l(uf) ≥2。

因此, 不妨设

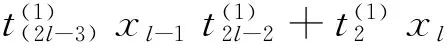
则

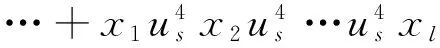
…+x1x2…xl+x1x2…xl

故B8是由(1)～(9)所决定的。证毕。

容易验证,B8满足

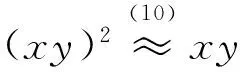
(10)

定理3B8是由等式(3)～(5),(9), (10) 所决定的。

证 明由式(10)，得

x3≈x6≈x4x2≈x2x2≈x4≈x2,

即

进一步，有

因此,等式(3),(10)可以演绎出(1)。同理可证(3),(10)可以演绎出(1)。

下证(1)～(5)，式(9)可以演绎出(6),(7),(8)。事实上,

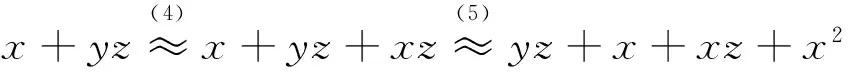
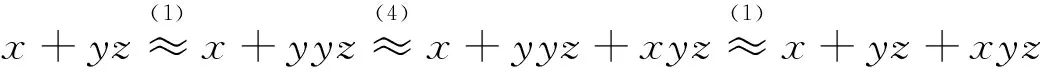
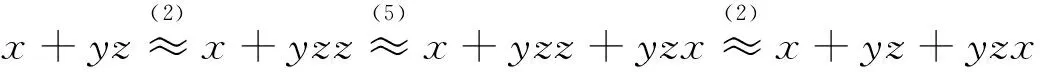
因此, B8是由(3)～(5),(9),(10)所决定的。证毕。

致谢：作者感谢导师赵宪钟教授的指导!

[1]PERKINS P. Bases for equational theories of semigroups[J].J Algebra，1968, 11：298-314.

[2]DOLINKA I. A nonfintely based finite semiring[J].Internat J Algebra Comput，2007, 17(8):1537-1551.

[3]DOLINKA I. A remark on non-finitely based semirings[J].Semigroup Forum, 2009, 78: 368-373.

[4]BIRKHOFF G. On the structure of abstract algebras[J].Proc Camb Philos Soc, 1935,31:433-454.

[5]BURRIS S, SANKAPPANAVAR H P. A Course in Univeral Algebra[M]. New York：Springer, 1981.

[6]GHOSH S, PASTIJN F, ZHAO X Z. Varieties Generated by Ordered Bands I[J].Order, 2005, 22: 109-128.

[7]MONCO C S.On finite congruence-simple semirings[J].J Algebra, 2004, 271:846-854.

[8]PASTIJN F. Varieties generated by ordered bands II[J]. Order,2005, 22, 129-143.

[9]PASTIJN F, ZHAO X Z. Varieties of idempotent semirings with commutative addition[J]. Algebra Univers, 2005, 54: 301-321.

[10] SHAO Y, REN M M. On the varieties generated by ai-semirings of order two[J]. Semigroup Forum, 2014， 89:1-14.

[11] SHAO Y, REN M M. The variety of semirings generated by distributive lattices and prime fields[J]. J Math Res Appl, 2014, 34(5): 529-534.

[12] ZHAO X Z. Idempotent semirings with a commutative additive reduct[J]. Semigroup Forum, 2002, 64: 289-296.

[13] HOWIE J M. Fundementals of Semigroup Theory[M].Oxford：Oxford University Press, 1955.

[14] HEBISCH U, WEINERT H J. Semirings-Algebraic Theory and Applications in Computer Science[M].Singapore：World Scientific, 1998.

[15] REN M M, ZHAO X Z. On free Burnside ai-semirings[J]. Semigroup Forum, 2015, 90(1): 174-183.

(编辑亢小玉)

Varieties generated by some semirings of order two

ZHANG Ke, REN Miao-miao, SHAO Yong

(School of Mathematics, Northwest University, Xi′an 710127， China)

In this paper the varieties generated by some semirings of order two are studied. The word problem for these varieties is solved, proving that they are all finitely based. Moreover, equational basis is given for each of them.

semiring; identity; equational basis; variety

2015-05-10

陕西省自然科学基金资助项目(2015JQ1210)

张可,女,陕西西安人，从事半群代数理论、半环研究。

O153.3

A

10.16152/j.cnki.xdxbzr.2016-03-006