行人荷载随机性对楼盖振动响应的影响研究*

丁　国， 陈　隽,2

(1.同济大学土木工程学院建筑工程系，上海 200092；2.土木工程防灾国家重点实验室，上海 200092)



行人荷载随机性对楼盖振动响应的影响研究*

丁国1， 陈隽1,2

(1.同济大学土木工程学院建筑工程系，上海 200092；2.土木工程防灾国家重点实验室，上海 200092)

首先基于大量实验数据构建了行人单步步行荷载模型，并利用频率拓展方法获得了连续步行荷载时程，通过引入步频变异系数反映个体内随机性，引入体重及均值步频的变化反映个体间随机性。采用概率密度演化方法对一典型大跨楼盖实例进行了行人作用下的振动响应分析，与蒙特卡洛模拟结果的对比说明了概率密度演化方法中所采用的代表点能够合理反映出所选随机参数的主要概率信息。在此基础上，采用极值概率密度演化方法获得了楼盖10 s均方根加速度的概率分布，并给出了具有95%和75%保证水平的反应谱曲线。与不考虑荷载随机性的楼盖振动响应结果对比发现，对于95%保证水平，行人荷载随机性放大效应最大可超过4倍，对于75%保证水平最大也接近2.5倍。结果表明，行人荷载随机性对楼盖的振动响应具有显著的影响，在楼盖的舒适度评估中需要考虑行人荷载的随机性。

行人荷载； 大跨楼盖； 荷载随机性； 概率密度演化； 振动响应

引　言

行人步行荷载作用下的振动舒适度问题已经成为大跨结构设计的重要控制因素[1]，在大跨楼盖[2]、大跨人行桥[3]、空中连廊等结构设计中日益受到重视。针对行人荷载，国内外学者已做了大量研究，提出了多种步行荷载模型，其中绝大多数都是假定步行力为确定性周期荷载。但实验结果均反映出，由于个体间和个体内差异，行人荷载具有很大的随机性[4]。然而，目前考虑行人荷载随机性对结构的振动舒适度评价以及结构适用性的可靠度分析影响的研究还非常缺乏。

行人个体内与个体间的差异所带来的随机性，使得行人荷载随机性分析成为高维随机振动问题，采用传统的随机动力分析方法(如随机摄动法、蒙特卡洛模拟(Monte Carlo simulation, MCS)等)难以求解。近年来，不断发展完善的概率密度演化方法(Probability density evolution method, PDEM)，以物理量为考察对象，从解耦状态方程出发，很好地解决了高维情况难以求解问题，以其高效、精细的优势，为结构随机动力响应以及可靠度分析开拓了新思路[5-6]。PDEM可精确获得结构响应的概率信息，应用于本研究中可有效降低计算量，在计算效率上具有显著的优势。鉴于行人荷载随机性对结构振动响应的影响还不甚明确，本文针对大跨度楼盖，采用PDEM分析研究行人荷载随机性对其振动响应的影响。

1　单步步行荷载模型的构建

本研究小组采用三维动作捕捉技术结合固定测力板开展了针对中国人的步行荷载实验建模研究[7]。经过数据质量检验，实验中共获得4814条有效的单足落步时程曲线，如图1所示典型曲线。本文假定左右脚的步行力服从相同变化规律，则可进行竖向单步步行荷载模型的构建。

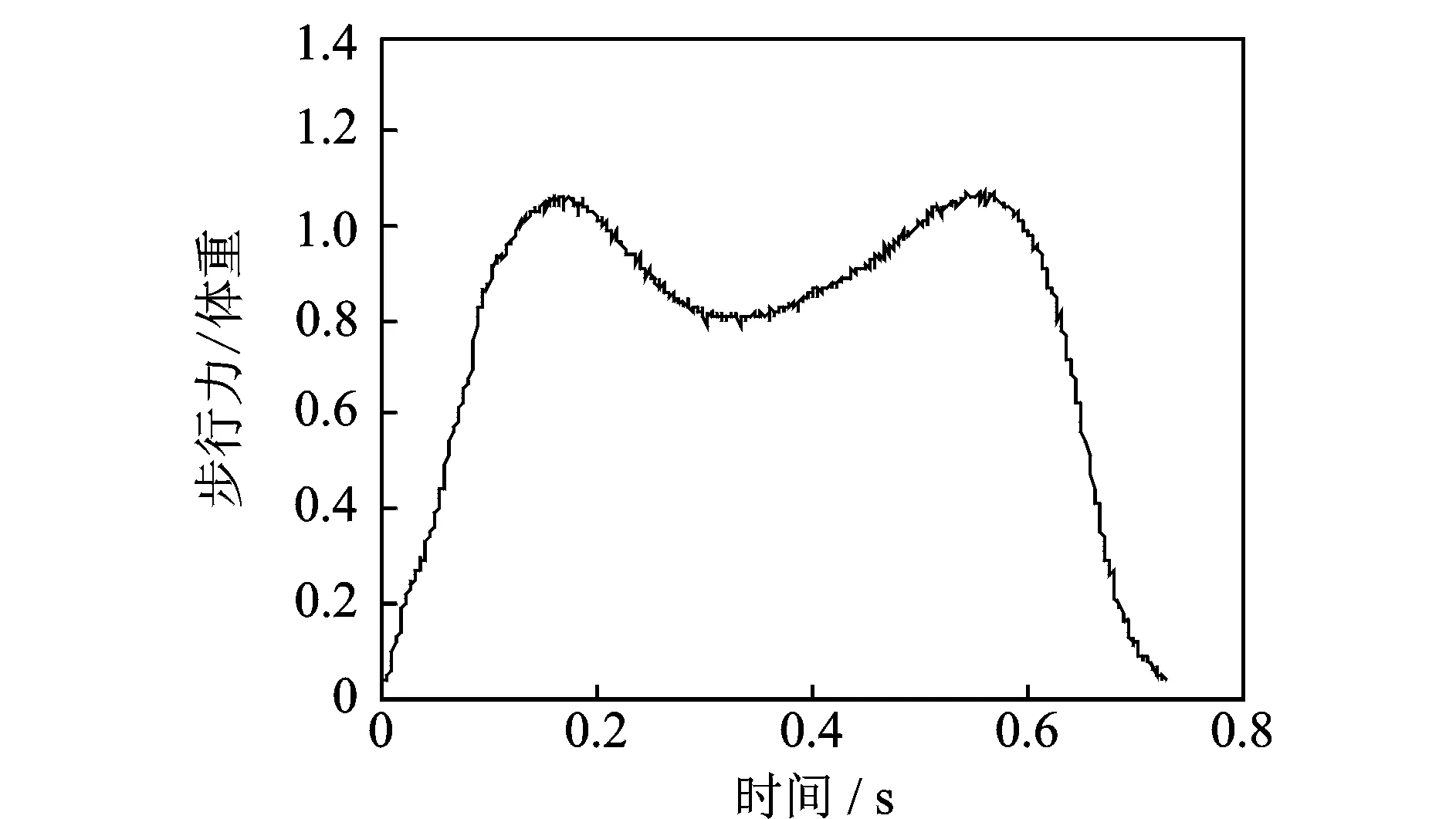
图1　典型实测竖向单足落步时程曲线Fig.1　Typical single footfall curve in vertical direction

采用傅里叶级数建立单步步行荷载模型，取正交谐波基函数，并考虑步行荷载与人体体重相关，则有

(1)

式中

Fz(t)为实测单步荷载，ai和bi为傅里叶系数，αi为第i阶动载因子(Dynamic loading factor,DLF)，φi为对应第i阶相位角，T为单步时程持续时间，ω=2π,T为基波角频率，G为人体体重，n为所考虑的谐波阶数。

单足落步时程曲线的形状变化与步行快慢直接相关，因此将步频作为基本参考量，分别统计单步持时T、各阶动载因子αi及相位角φi与步频fp的关系。持时T、常数项a0与步频的统计关系见下式

(2)

a0=0.0310×fp+0.7500

(3)

对应的拟合结果分布见图2，3。

单步步行荷载模型须准确表达实际步行荷载的时、频域特征，故分别从单足落步时程曲线的时域、扩展成连续步行时程曲线的时域和频域三方面分别与实测时程曲线进行对比，分析表明取前8阶谐波方可保证模型的精确性。由实验拟合获得的各阶动载因子与相位角取值如表1所示。

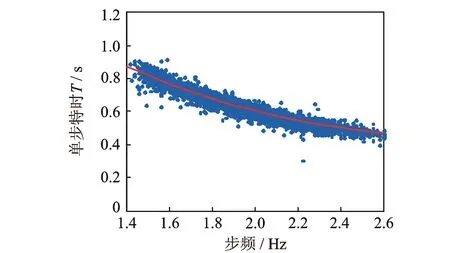
图2　单步持时与步频的关系Fig.2　Relationship between single stride period and walking frequency

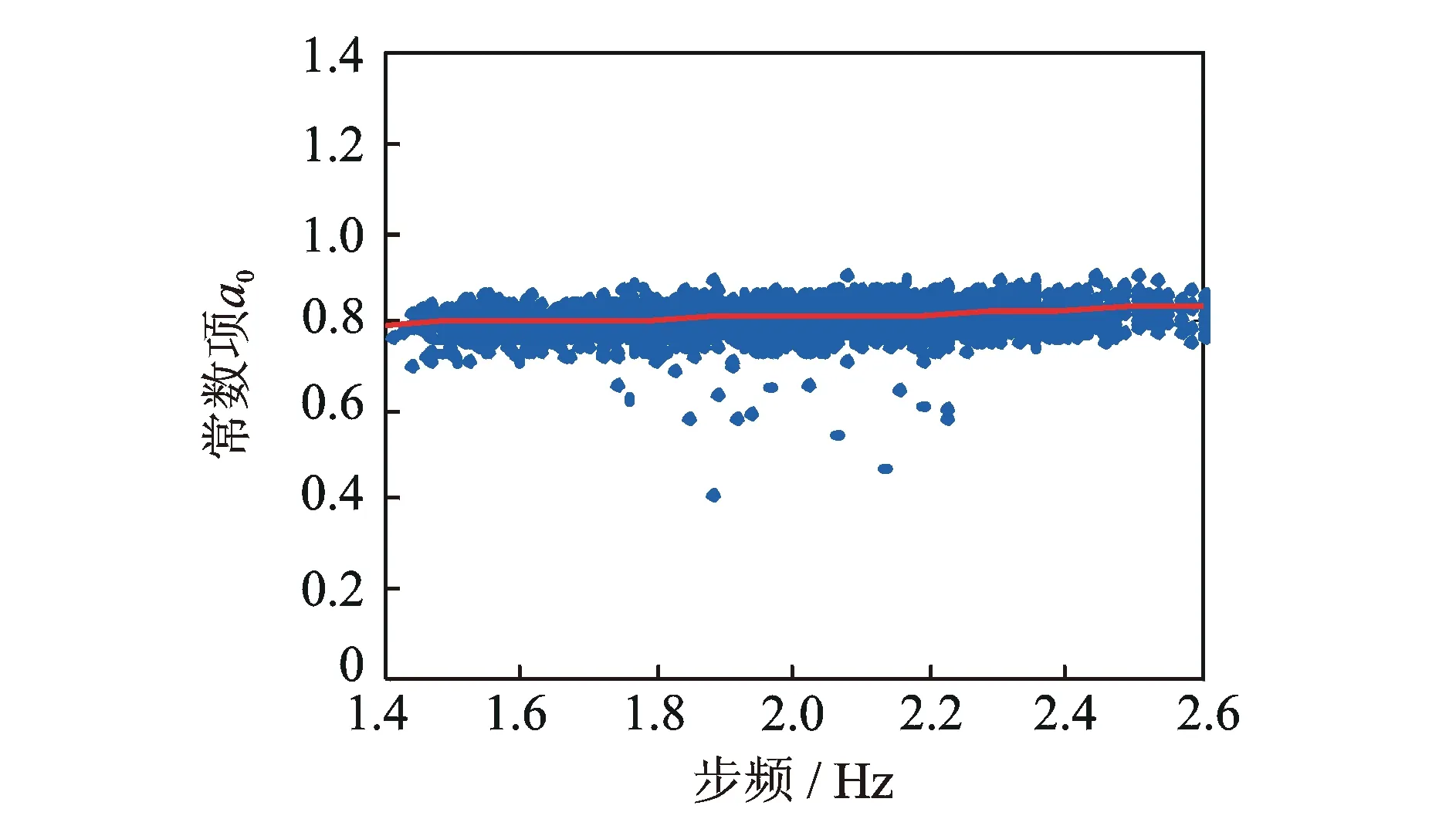
图3　常数项a0与步频的关系Fig.3　Relationship between the constant a0 and walking frequency

统计中，前4阶动载因子和相位角与步频存在较强的相关性，分别采用多项式函数进行最小二乘拟合，其中1，2阶动载因子和相位角拟合结果如图4所示；5～8阶动载因子与步频相关性不明显，取其统计均值。表1中给出的动载因子与相位角取值适用步频为1.4～2.6 Hz，实测表明此范围基本涵盖了正常行走的步频。

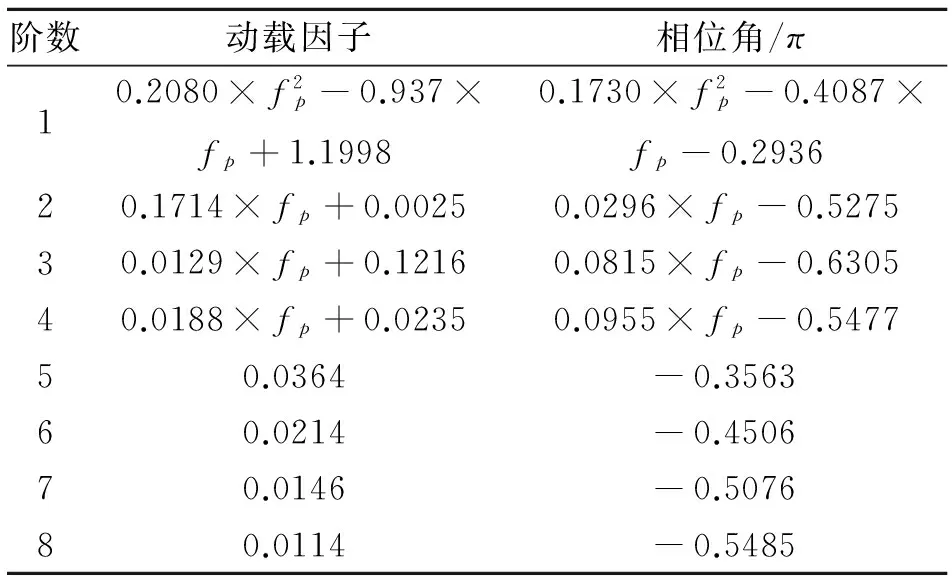
表1　单步步行荷载模型动载因子与相位角

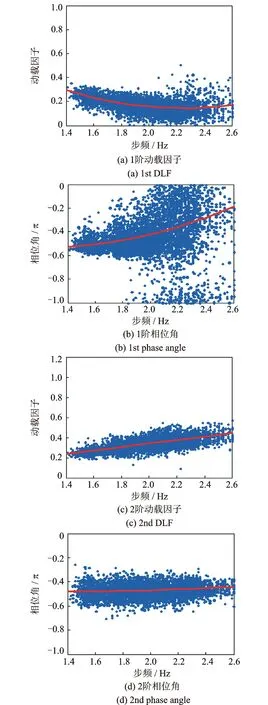
图4　1、2阶动载因子和相位角随步频变化Fig.4　DLFs and phase angle varied with walking frequency

行人荷载的时域、频域特征及动力特性分析均是针对连续步行荷载，因此，必须采取一定方法将单步时程曲线拓展成连续时程曲线。研究表明，采用按步频和步行时间两种拓展方法最为合理[8]。本研究中采用按步频拓展方法进行单足落步时程曲线的拓展，即两曲线的前后时间间隔为1/fp。其中后续分析中采用代表点生成的典型单足落步时程曲线及拓展后的连续步行时程曲线及Fourier幅值谱如图5所示，均值步频为1.967 Hz。

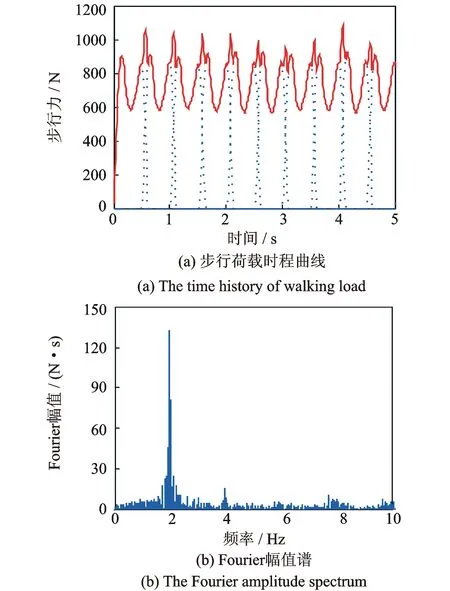
图5　典型步行荷载Fig.5　The typical walking load curve

2　行人荷载随机性特征

行人荷载的随机性来源于多方面，包括步行者的特征、行走路线、多人行走时的人与人之间的距离，甚至楼盖的动力特性等。由于试验研究目前仍主要集中在单人行走激励上，一般认为单人行走荷载的随机性主要来源于个体间差异和个体内差异，前者表示不同步行者的步行力不完全相同，后者表示同一步行者每步并非完全一致[4]。

2.1个体间随机性

个体间随机性主要是由步行者的体重和步频的差异产生。对于体重的随机性，研究中假定步行者为健康成年人，体重服从对数正态分布，均值为73.85 kg，标准差为15.6 kg[9]。

为了得到自由步行状态下步行频率的分布，统计了实验中自由步行工况下的742条实测单足落步时程对应的步频数据，如图6所示。步频分布服从正态分布，其均值为2.1 Hz，标准差为0.163 Hz(图中实线)。Matsumoto等[10]曾对步行频率进行统计研究，样本量为505人，认为步行频率服从期望为2.0 Hz，标准差为0.173 Hz的正态分布，与本研究的结论大致相同。

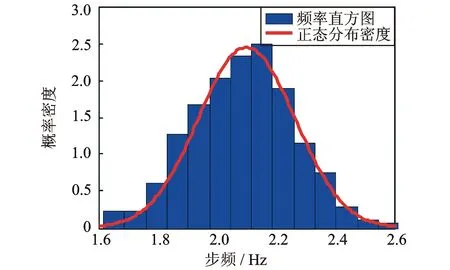
图6　自由行走步频分布统计Fig.6　Distribution statistics of free walking frequency

除体重和步频两个主要参数外，分析中还进一步考虑了测试者每次行走时首次踏点的随机性，假定踏点位置在距楼板边缘[0,ΔL]内服从均匀分布。ΔL为单步步幅，实验统计如图7所示，单步步幅随步频变化并不明显，取均值0.67 m。

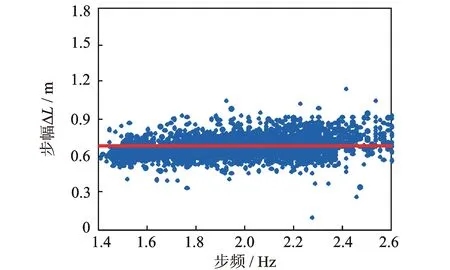
图7　单步步幅与步频关系Fig.7　Relationship between single stride length and walking frequency

2.2个体内随机性

单人在一次步行过程中步频等参数不会发生剧烈变化，但亦不会产生完全一致的一系列单步，把单人行走中部分参数发生小量的变化称为个体内参数的随机性。考虑到步频为前述各参数的共同参考量，本研究仅考虑个体内步频的随机性。

为分析个体内参数随机性，对每一个测试者样本每一种工况内参数的变异性作统计。将每一个测试者样本每种工况下的多条数据归作一组，认为一组内数据参数的变异性是由个体内差异产生的。定义个体内变异系数ξ为每一组参数数据与该组参数数据均值的比

(4)

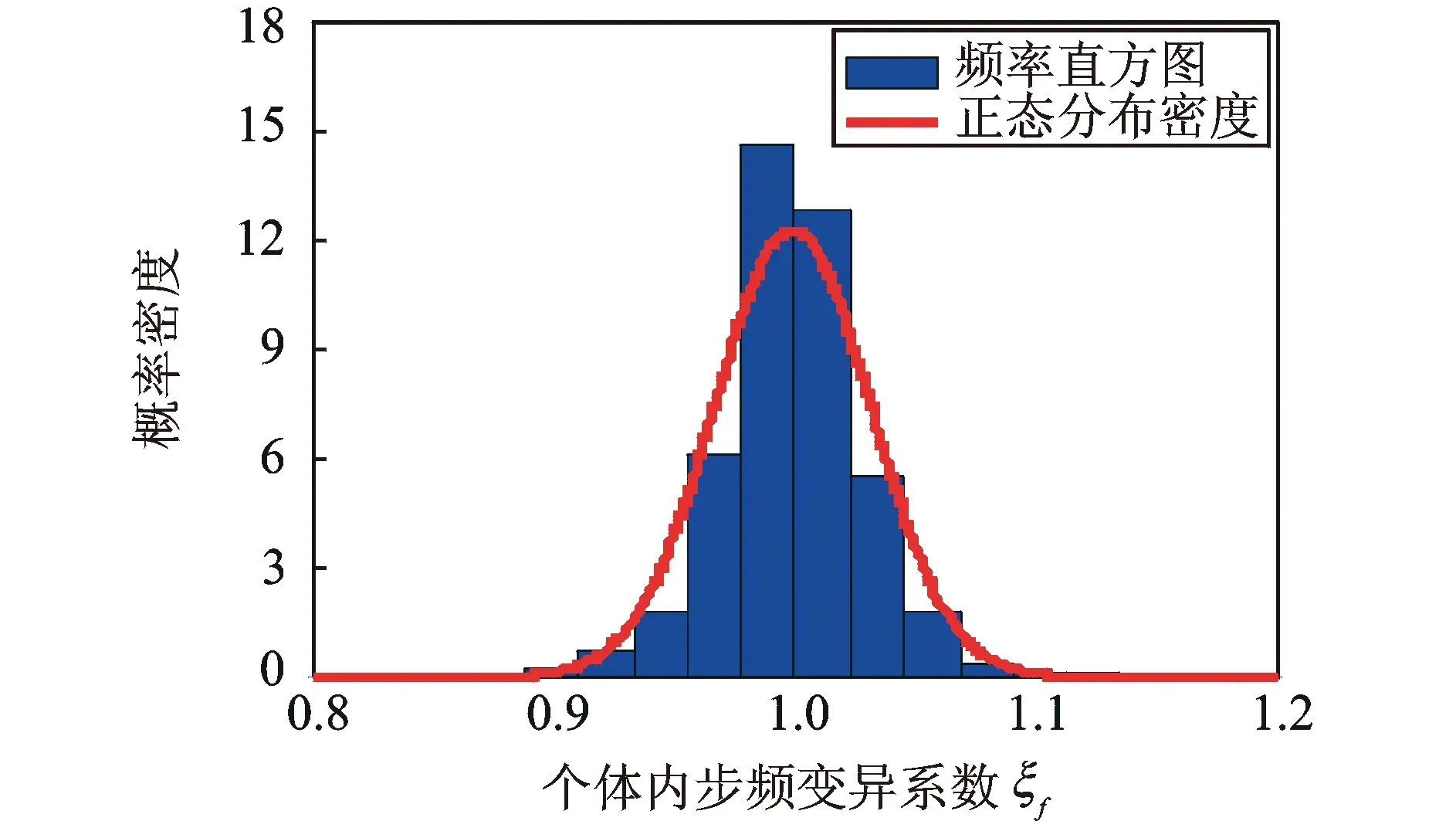
图8　个体内步频变异系数分布统计Fig.8　Distribution statistics of intra-subject walking frequency variability

3　随机动力分析的PDEM方法

文献[11-12]已详细描述了广义概率密度演化方程的推导过程以及PDEM求解步骤，这里根据所研究问题需要，简要介绍极值概率密度演化方法及其数值解法。

3.1极值概率密度演化方法

随机动力分析中，随机性通常来自结构和激励两部分，取基本随机向量Θ=(ξ1,ξ2)=(Θ1,Θ2,…,Θs)，其中，随机向量ξ1刻画结构系统的随机性，ξ2刻画激励的随机性。因此，随机结构的动力反应控制方程可表示为

(5)

式中M，C分别为系统的质量与阻尼矩阵，G(·)为线性或非线性恢复力向量，Γ为激励影响矩阵，F为激励向量。

记Z=(Z1,Z2,…,Zm)T为所考察物理量构成的向量，由文献[12]的推导，广义概率密度演化方程为

(6)

式中θ为随机向量Θ的样本值。当仅对某一个物理量感兴趣时(即m=1)，方程(6)退化为一个一维偏微分方程。

在楼盖振动舒适度分析中，通常所关心的是加速度或均方根加速度响应的最大值，可通过等价极值[13]获得。定义随机过程X(Θ,t)的极值

(7)

构造一个虚拟时间参数的虚拟随机过程

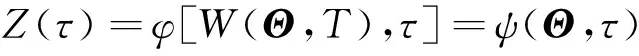
(8)

使得它满足条件

(9)

虚拟随机过程Z(τ)的随机性完全来源于Θ， (Z(τ),Θ)构成一个概率保守系统，其联合概率密度函数pZΘ(z,θ,τ)满足如下广义概率密度演化方程

(10)

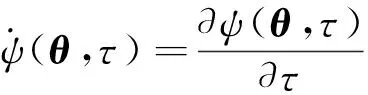
求解方程(9)和(10)获得pZΘ(z,θ,τ)后，即可进一步得到Z(τ)的概率密度函数

(11)

从而有

(12)

其中，pXext(x)就是所要获得的Xext的概率密度函数。

本研究后续分析中选取式(8)为

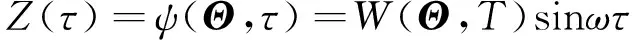
(13)

其中，ω=2.5π，τc=1。

3.2数值解法

在3.1中介绍的极值概率密度演化方法可通过数值解法实现，具体流程如图9所示。

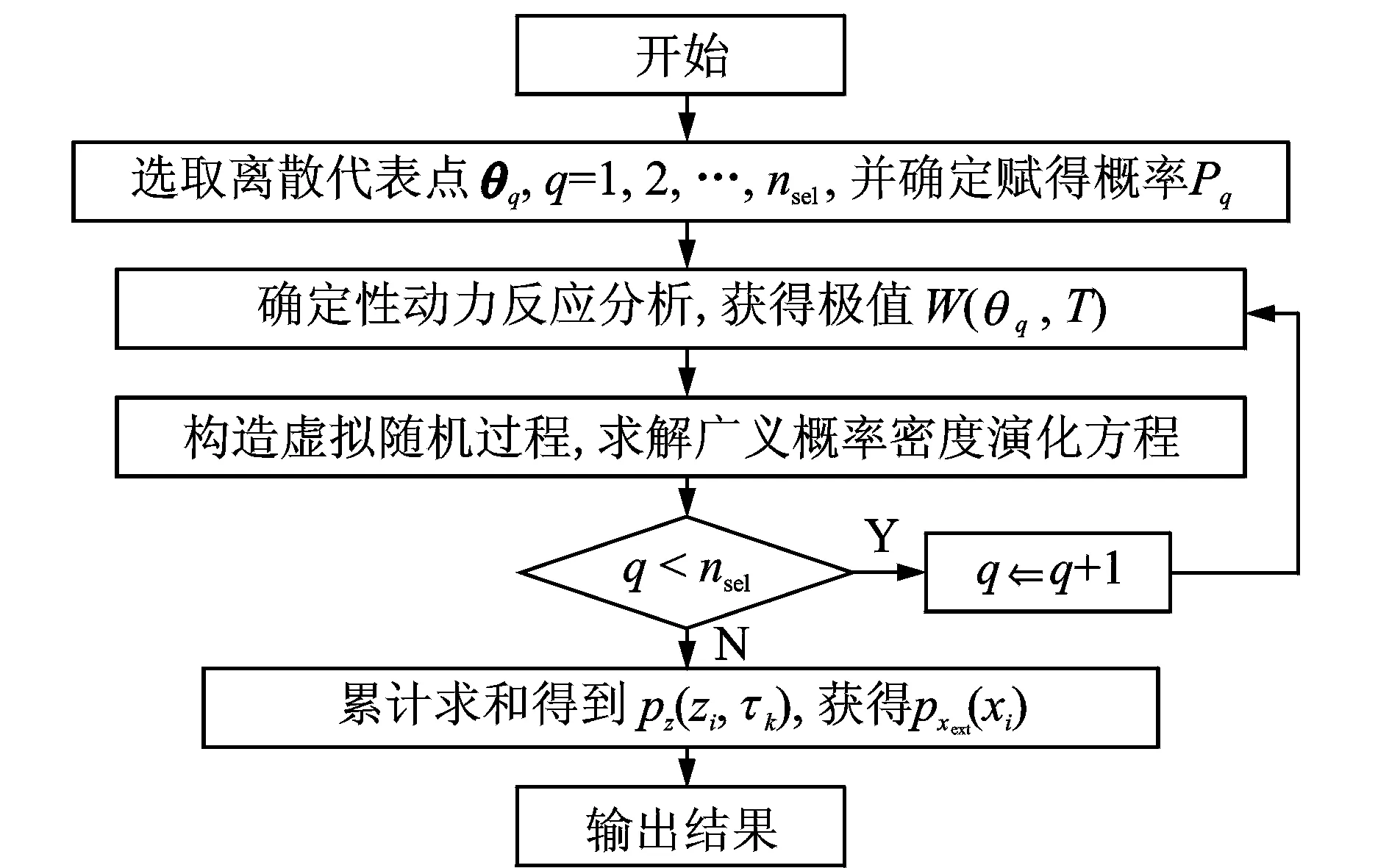
图9　数值解法流程图Fig.9　Numerical solution flowchart

基于Sobol点集可生成任意维度任意点数的低偏差点集，本研究相关分析中采用Sobol点集及相关调整方法进行离散代表点的选取。后续分析中综合考虑个体间和个体内参量的随机性，并将单步间的个体内步频变异系数视为独立同分布随机变量，共计65个随机变量，选取1024个Sobol点作为初始点集，按下式进行坐标调整来降低广义F偏差(GF偏差)[14]，并重新计算点集的赋得概率。

(14)

图10　调整前后概率分布示意图Fig.10　PDF schematic diagram before and after coordinate adjustment

采用具有TVD性质格式的有限差分方法[11]求解方程(10)，z，τ两方向均匀离散，即zi=iΔz，τk=kΔτ，其中i=0,±1,±2,…;k=0,1,2,…。

4　行人荷载随机性影响分析

综合考虑第2节中所确定参数的随机性，步行荷载由第1节给出的单步步行荷载模型生成并拓展成连续步行荷载，采用PDEM对某楼盖进行振动响应分析，进一步采用第3节中所述极值概率密度演化方法获得10sRMS加速度反应谱，综合分析行人荷载随机性对楼盖振动响应的影响。

4.1实例分析

某体育中心综合训练馆预应力混凝土楼盖尺寸72m×42m，短轴方向有10根450mm×3000mm的预应力梁，间距8000mm，长轴方向普通混凝土梁的尺寸为250mm×800mm，另外在长轴方向预应力梁底部由钢管支撑，钢管内径为48mm、壁厚3.5mm。混凝土板的厚度为120mm，梁板采用C50混凝土浇注。采用Ansys有限元软件建模(图11)并进行模态分析，获得楼盖的模态信息，如表2所示，振型阻尼比由实测分析获得[15]。

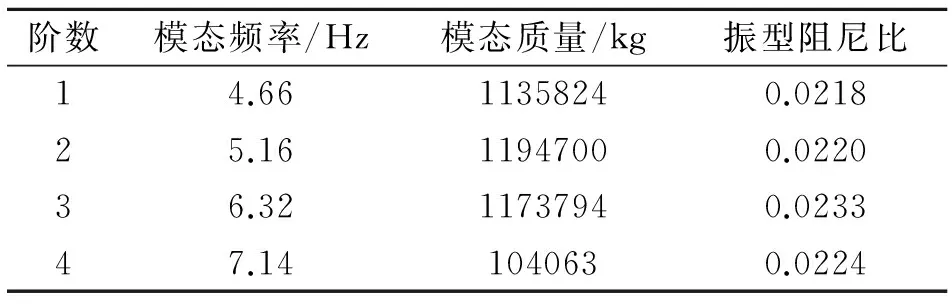
表2　楼盖模态信息

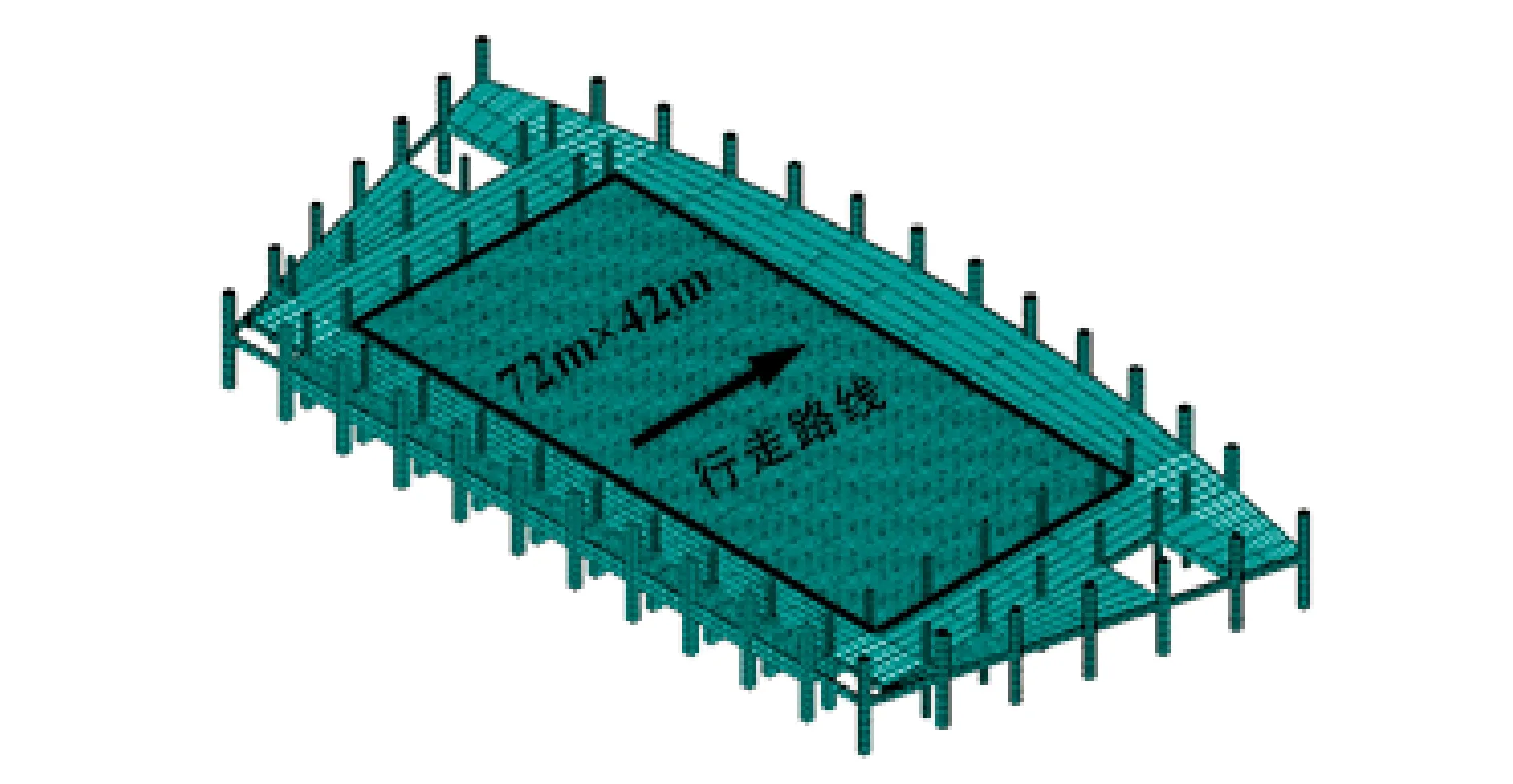
图11　楼盖有限元模型Fig.11　Finite element model of the floor

行人荷载作用下，楼盖发生弹性振动，可采用振型分解法进行振动响应分析。对于大跨楼盖，动力响应主要受第一阶振型控制，其他阶贡献相对较小，最大加速度出现在跨中位置[2]。本文从有限元模型中提取前3阶振型进行楼盖短轴方向的振动响应分析，采用PDEM可获得整个加载过程跨中节点加速度响应的概率分布信息。其中典型时段的概率密度演化曲面如图12所示，典型时刻的概率密度曲线如图13所示。

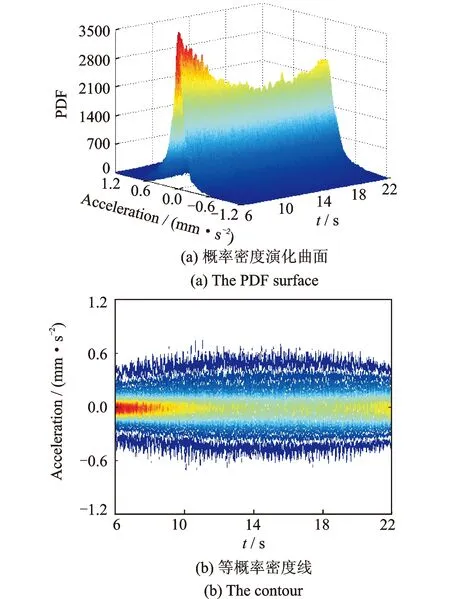
图12　典型时段的概率密度演化曲面Fig.12　PDF evolution surface and the contour

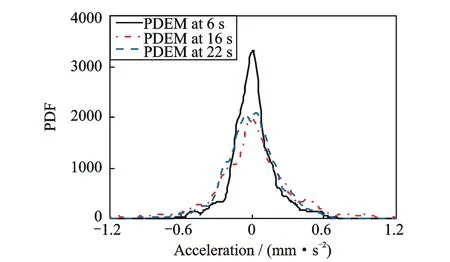
图13　典型时刻概率密度曲线Fig.13　The typical PDF at different time instants

从图12可看出，楼盖跨中节点最大加速度响应出现在行人位于跨中位置时刻(约16 s左右)，在此时刻之前，概率密度峰值逐渐减小，加速度响应分布区间逐渐扩大；此时刻之后，概率密度曲面变化与前述相反。整个加载过程中，加速度响应的概率密度演化缓慢，曲面呈单峰。典型时刻的概率密度曲线大体类似正态分布，但有时表现出明显偏态性质。上述结果与MCS 100000次模拟结果吻合良好，如图14所示，进一步说明PDEM分析中采用1024个代表点能够合理反映出所选随机参数的主要概率信息。

各国规范普遍认为行人对振动的不舒适感主要受加速度控制。对加速度的计算方法主要分为最大加速度法(amax)、均方根加速度法(arms)和振动剂量法(aVDV)，目前应用最广的是均方根加速度法，本文采用10 s均方根加速度反应作为楼盖振动的衡量指标。因此，进一步采用极值概率密度演化方法，获得上述楼盖行人荷载下跨中节点10 s RMS加速度响应的概率分布信息，如图15所示，与一般的极值分布在细节上有所不同。从图15(b)看出，极值概率密度演化方法的结果与MCS结果一致，具有较高精度。

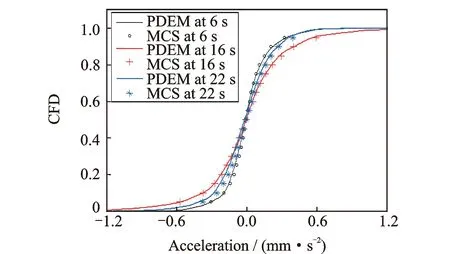
图14　典型时刻概率分布函数曲线Fig.14　The typical CDF at different time instants

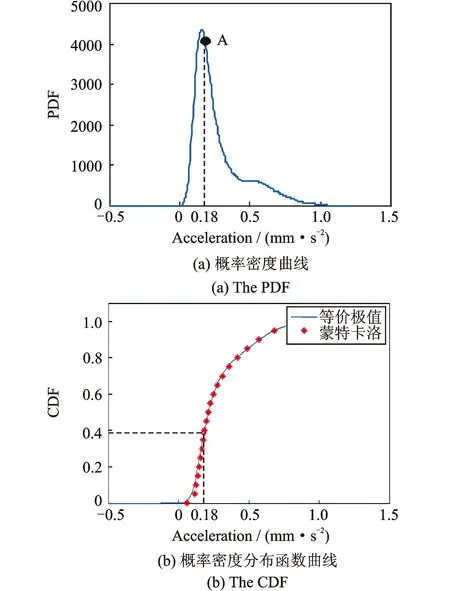
图15　10 s RMS加速度响应的概率密度曲线与分布函数曲线Fig.15　PDF and CDF of the 10s RMS acceleration response

4.2行人荷载随机性影响分析

针对实例楼盖，进一步分析获得不考虑荷载随机性(各参数取均值)下的10 s RMS加速度值，示于图15中点A，对应于考虑荷载随机性时振动响应的38.6%保证水平。该结果表明，考虑荷载随机性下的最大10 s RMS加速度值远大于不考虑荷载随机性下的最大10 s RMS加速度值，说明不考虑行人荷载随机性进行楼盖振动响应分析与舒适度评估是过于不安全的。

楼盖的振动响应和行人荷载的频谱成分及楼盖自身频率密切相关，因此，本文进一步从反应谱上分析行人荷载随机性对大跨楼盖振动响应的影响。文献[16]的研究工作表明，不同振型和边界条件的反应谱间具有转换关系。因此，为简便以下分析中仅考虑楼盖第一阶振型反应，振型取为半正弦曲线，楼盖跨度按目前国内最大跨度取42 m，振型阻尼比取2%。

为分析行人荷载随机性对大跨楼盖振动响应的影响，分别计算不考虑荷载随机性、考虑荷载随机性和仅体重取95%保证率(其他参数取均值)三种情况下的10 s RMS加速度反应谱，其中不考虑荷载随机性下各随机参数取分布均值，考虑荷载随机性下各随机参数按2.1节和2.2节中的对应分布取值，如图16所示，图中对于考虑荷载随机性情况给出了95%和75%保证水平的反应谱曲线。为更直观反映出荷载随机性对楼盖振动响应的放大效应，上述两个保证水平的反应谱曲线与不考虑荷载随机性下的反应谱曲线的比值分别示于图17中。

图16　楼盖10 s RMS加速度反应谱Fig.16　The 10 s RMS acceleration response spectrum curve

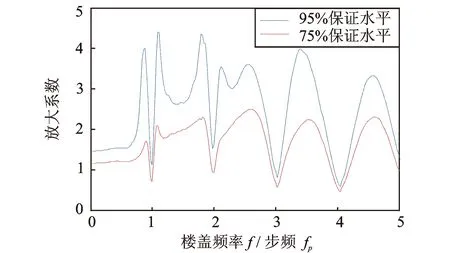
图17　步行荷载随机性对振动响应的放大效应Fig.17　The amplification effect of walking load randomness on vibration responses

对比图中曲线可以得出以下几点：

(1)由于共振效应，反应谱曲线在步频的倍频处出现峰值，对于考虑荷载随机性情况，反应谱共振频段范围明显增大，且95%和75%保证水平曲线均位于不考虑荷载随机性曲线的上方。不考虑荷载随机性的计算结果偏小，因此，进一步说明了不考虑行人荷载随机性进行楼盖振动响应分析与舒适度评估是偏于不安全的，难以保证规定的舒适性要求。

(2)对于不同频率楼盖，行人荷载随机性的放大效应也不同，在步频的倍频处放大效应最小，接近甚至小于1；在倍频左右两侧放大效应急剧增大，并在两倍频间达到最大，对于95%保证水平曲线最大可超过4倍，对于75%保证水平曲线最大也接近2.5倍。行人荷载随机性对于非步频的倍频频率的楼盖影响较为明显，需考虑荷载随机性以更接近实际情况。

(3)从步行荷载模型上看出，对于线弹性反应，体重与响应呈线性关系，仅体重取95%保证率的反应谱曲线示于图17中虚线。在步频的倍频处接近甚至超过考虑荷载随机性情况下95%保证水平值，但在非步频倍频上仍小于75%保证水平值。说明仅从体重上取一定水平的保证值进行振动响应分析与舒适度评价也是不合理的。

考虑步频、体重等参数的随机性更接近实际步行情况，因此，考虑行人荷载随机性进行楼盖的振动响应分析与舒适度评估更为合理。同时通过本文的大量分析发现，正如图17中曲线所呈现出的无规律性，工程实际中并不能通过简单的在均值响应基础上引入比例系数的方式来考虑步行荷载随机性的影响，而仍需要采用随机动力分析方法进行考虑荷载随机性的楼盖振动响应分析与舒适度评估。

5　结　论

(1)本文基于实验数据构建的单步步行荷载模型，可用于楼盖振动响应与舒适度评估的精细化分析。模型参数的分布特性由实验数据统计得到，可真实地反映出行人荷载的随机性。

(2)行人荷载随机性对楼盖振动响应具有显著的影响，特别是对于非步频倍频的楼盖。就本文算例，对于95%保证水平，行人荷载随机性放大效应最大可超过4倍，对于75%保证水平最大也接近2.5倍。因此，不考虑行人荷载随机性进行楼盖振动响应分析与舒适度评估是偏于不安全的。

(3)分析表明，行人荷载随机性对楼盖振动响应的影响大小与楼盖自身频率相关，现有分析方法无法有效地考虑其随机性的影响，因此仍需采用随机动力分析方法来考虑荷载的随机性。PDEM在求解高维随机问题具有高效、精细优势，可应用于行人荷载作用下楼盖随机振动响应与舒适度评估分析。

[1]折雄雄，陈隽．大跨度楼盖振动舒适度研究综述[J]．结构工程师，2009，25(6)：144—149．

She Xiongxiong，Chen Jun．A review of vibration serviceability for long-span floors[J]．Structural Engineers，2009，25(6)：144—149．

[2]宋志刚，金伟良．行走激励下大跨度楼板振动的最大加速度响应谱方法[J]．建筑结构学报，2004，25(2)：57—63．

Song Zhigang，Jin Weiliang．Peak acceleration response spectrum of long span floor vibration by pedestrian excitation[J]．Journal of Building Structures，2004，25(2)：57—63．

[3]聂建国，陈宇，樊健生．步行荷载作用下单跨人行桥振动的均方根加速度反应谱法[J]．土木工程学报，2010，43(9)：109—116．

Nie Jianguo，Chen Yu，Fan Jiansheng．RMS acceleration response spectrum method for single-span footbridges under pedestrian load[J]．China Civil Engineering Journal，2010，43(9)：109—116．

[4]Racic V，Pavic A，Brownjohn J．Experimental identification and analytical modelling of human walking forces: Literature review[J]．Journal of Sound and Vibration，2009，326(1-2)：1—49．

[5]Chen J B，Li J．Dynamic response and reliability analysis of non-linear stochastic structures[J]．Probabilistic Engineering Mechanics，2005，20(1)：33—44．

[6]李杰，陈建兵．随机结构动力可靠度分析的概率密度演化方法[J]．振动工程学报，2004，17(2)：121—125．

Li Jie，Chen Jianbing．Probability density evolution Method for dynamic reliability analysis of stochastic structures[J]．Journal of Vibration Engineering，2004，17(2)：121—125．

[7]陈隽，彭怡欣，王玲．基于步态分析技术的三向单足落步曲线的实验建模[J]．土木工程学报，2014，47(3)：79—87．

Chen Jun，Peng Yixin，Wang Ling．Experimental investigation and mathematical modeling of single footfall load using motion capture technology[J]．China Civil Engineering Journal，2014，47(3)：79—87．

[8]Chen J，Peng Y X，Ye T．On methods for extending a single footfall trace into a continuous force curve for floor vibration serviceability analysis[J]．Structural Engineering and Mechanics，2013，46(2)：179—196．

[9]Portier K，Tolson J K，Roberts S M．Body weight distributions for risk assessment[J]．Risk Analysis，2007，27(1)：11—26．

[10]Matsumoto Y，Sato S，Nishioka T，et al．A study on design of pedestrian over-bridges[J]．Transactions of JSCE，1972，4：50—51．

[11]Li J，Chen J B．Stochastic Dynamics of Structures[M]．Singapore：John Wiley & Sons (Asia) Pte Ltd.，2009：191—311．

[12]Li J，Chen J B．The principle of preservation of probability and the generalized density evolution equation[J]．Structural Safety，2008，30(1)：65—77．

[13]Li J，Chen J B，Fan W L．The equivalent extreme-value event and evaluation of the structural system reliability[J]．Structural Safety，2007，29(2)：112—131．

[14]陈建兵，张圣涵．非均布随机参数结构非线性响应的概率密度演化[J]．力学学报，2014，46(1)：136—144．

Chen Jianbing，Zhang Shenghan．Probability density evolution analysis of nonlinear response of structures with non-uniform random parameters[J]．Chinese Journal of Theoretical and Applied Mechanics，2014，46(1)：136—144．

[15]陈隽，折雄雄，刘秦生．青岛体育中心综合训练馆大跨混凝土楼盖振动舒适度测试与分析[J]．建筑结构．2011，41(8)：115—119．

Chen Jun，She Xiongxiong，Liu Qinsheng．Modal testing and vertical vibration serviceability analysis of large-span pre-stressed concrete floor of Training Hall in Qingdao Sport Center[J]．Building Structure,2011，41(8)：115—119．

[16]Chen J，Xu R T，Zhang M S．Acceleration response spectrum for predicting floor vibration due to occupant walking[J]．Journal of Sound and Vibration，2014，333：3564—3579．

Influences of walking load randomness on vibration responses of long-span floors

DINGGuo1,CHENJun1,2

(1．Department of Structural Engineering, College of Civil Engineering, Tongji University, Shanghai 200092, China;2．State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

A single footfall load model of pedestrian has been developed based on a large number of experimental records. The continuous time history of walking load is then expanded from the single footfall load curve by assuming it is a periodic one. Intra-subject variability, such as variation of body weight and mean walking rate, is one source for randomness in walking load. The other source is inter-subject variability, which is represented by variation coefficient of mean walking frequency. The probability density evolution method (PDEM) is adopted to calculate the dynamic responses of a long-span floor subjected to random walking load. The probability distribution of 10-sec root-mean-square acceleration responses are obtained by using the extreme value probability density evolution method, and the response spectrum curves with 75% and 95% confidence level are given in the study. Comparison of responses with and without consideration of walking load randomness shows that the acceleration responses of the floor could be underestimated without considering the walking load randomness. The walking load randomness should be considered in the assessment of vibration serviceability of long-span floors.

walking load; long-span floor; load randomness; probability density evolution method (PDEM); vibration response

2014-04-07；

2015-03-18

国家自然科学基金资助项目(51478346)

TU375.2; TU312+.1

A

1004-4523(2016)01-0123-09

10.16385/j.cnki.issn.1004-4523.2016.01.016

丁国(1990—)，男，硕士。E-mail：zhgding@163.com

陈隽(1972—)，男，博士，教授。E-mail：cejchen@tongji.edu.cn