基于层次模糊熵和改进支持向量机的轴承诊断方法研究*

李永波， 徐敏强， 赵海洋, 黄文虎

(哈尔滨工业大学深空探测基础研究中心， 黑龙江 哈尔滨 150001)



基于层次模糊熵和改进支持向量机的轴承诊断方法研究*

李永波， 徐敏强， 赵海洋, 黄文虎

(哈尔滨工业大学深空探测基础研究中心， 黑龙江 哈尔滨 150001)

提出一种新的轴承故障特征提取方法——层次模糊熵 (Hierarchical Fuzzy Entropy ,HFE)。层次模糊熵包括层次分析和模糊熵计算。与多尺度模糊熵相比, 层次模糊熵既分析信号的低频分量又分析信号的高频分量，因而能提取更全面、准确的故障信息。改进支持向量机(Improved support vector machine based binary tree，ISVM-BT)相比其他多分类器具有识别率更高的优势，因此提出了一种基于层次模糊熵和改进支持向量机的轴承故障诊断方法。首先将HFE作为故障特征提取工具，然后将所得的特征向量输入到改进支持向量机进行模式识别。通过轴承故障诊断的工程应用，表明该方法可以有效提取轴承故障特征，实现轴承不同故障类型和故障程度的准确识别。

故障诊断； 层次模糊熵(HFE)； 改进支持向量机(ISVM-BT)； 滚动轴承

引　言

滚动轴承作为一种基础的机械构件，在工业领域中发挥着极其重要的作用。人们对滚动轴承的故障诊断进行了大量的研究[1-3]。对于轴承的故障诊断通常采用振动分析方法，通过振动信号采集、故障特征提取和模式识别进行轴承故障诊断。针对滚动轴承故障信号的非平稳、非线性特征，如何有效提取轴承故障信息是最重要的环节。近年来，已有多种非线性分析方法如小波分析、神经网络、支持向量机、经验模态分解、分形维数等。

Pincus[4-5]最早提出近似熵的概念，通过比较数据和其自身来反映时间序列的复杂度。Richman[6]在近似熵的基础上提出了样本熵，克服了近似熵自身匹配的缺点。由于近似熵和样本熵都采用阶跃函数定义相似性，这与实际样本类边缘比较模糊不符。为克服上述不足，陈伟婷[7]提出了模糊熵(Fuzzy Entropy)的概念。然而近似熵、样本熵和模糊熵只能从单一尺度上度量时间序列复杂性，与复杂度之间没有直接对应关系，Costa[8-9]等提出了多尺度熵概念，首先对时间序列进行空间尺度分割，然后计算每个尺度下样本的熵值，进而得到时间序列在不同尺度下的复杂度。郑近德[10]将粗粒分割与模糊熵相结合提出多尺度模糊熵，并将其应用于轴承不同类型故障的诊断中。

文献[11-12]指出多尺度熵只能分析时间序列的低频部分，忽略了高频成分，进而提出层次熵，它既可反映信号高频分量复杂度又可反映低频分量复杂度。本文在模糊熵的基础上，借鉴层次分析的思想，提出了一种新的熵值计算方法——层次模糊熵。由于测得的轴承振动加速度信号的故障信息频带分布比较丰富，只考虑信号中的低频成分不能完全提取隐藏故障特征。为了能够更加全面分析非线性、非平稳信号在各个频段的特征，本文将层次模糊熵作为故障特征提取的工具应用到滚动轴承故障诊断中。

二叉树的层次结构在二叉树支持向量机(SVM-BT)中发挥着重要作用。目前二叉树的层次结构的设计方法主要包括：类间样本距离法[13]和类内样本分布法[14]。其中类间样本距离是先分出距离最远的类，而类内样本分布法是先分出分布最广的类。基于两种方法的优点，设计一种新的可分性测度，称为ISVM-BT，可有效提高识别率[15]。

本文利用层次模糊熵提取故障特征，结合ISVM-BT提出了一种新的轴承诊断方法。在此基础上，将此方法与多尺度模糊熵进行比较。实验结果表明，该方法可有效完成轴承不同故障类型和程度的准确识别诊断。

1　多尺度模糊熵和层次模糊熵

1.1多尺度模糊熵

样本熵和模糊熵的定义参考文献[7,16], 为了更准确地描述时间序列的复杂性，Costa提出多尺度概念[8]。郑近德借鉴多尺度分析与模糊熵的概念提出了多尺度模糊熵(multi-scale fuzzy entropy，MFE)并将其应用到轴承故障诊断中[10]。MFE方法的计算流程如下：

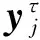
(1)

式中τ为尺度因子，τ=1,2,…，n(n为正整数)。

(2) 对于每一个得到的粗粒向量求取模糊熵，得到n个粗粒向量的模糊熵值，将其表示成尺度因子τ的函数，称为多尺度模糊熵分析。

(2)

式中相似容限r=(0.1～0.25)*SD，SD为原始序列的标准差。

从上述多尺度模糊熵的计算流程可以看出，多尺度模糊熵是从不同尺度因子上度量时间序列的复杂度。实际上，在多尺度模糊熵中，粗粒化的过程是求平均化的过程，即只考虑了原始序列的低频分量，忽略高频分量。对于故障信息主要分布较丰富的时间序列，多尺度模糊熵不能满足要求。为了提取信号中高频分量的故障信息，本文引入了层次模糊熵的概念，相比于多尺度模糊熵，层次模糊熵同时考虑了信号中低频分量和高频分量，从而能提供更加全面、准确的时间模式信息。

1.2层次模糊熵

江英提出了层次熵的概念，用于度量时间序列在不同节点处的复杂性，并将其成功应用到生物学信号分析中[11]。借鉴层次熵中层次分割的优势，结合模糊熵的定义，提出了层次模糊熵(hierarchical fuzzy entropy，HFE)的概念。与层次熵类似，层次模糊熵的计算流程如下：

(1) 给定长度为N的时间序列{u(i),i=1,2,…，N}，定义平均数算子Q0和Q1如下：

(3)

(4)

注：N=2n，n是正整数。算子Q0和算子Q1的长度为2n-1。根据算子Q0和Q1原始序列可重构为

(5)

当j=0或j=1,定义矩阵Qj算子如下

(6)

(2) 构造一个n维向量[γ1,γ2,…,γn]∈{0,1}, 则整数e可表示为

(7)

式中正整数e对应的向量为[γ1,γ2,…,γn]。

(3) 基于向量[γ1,γ2,…,γn]，定义时间序列u(i)每一层分解的节点分量如下

(8)

式中k表示层次分割中的第k层，如图1所示，原始时间序列u(i)在第k+1层的低频和高频部分分别用uk,0,uk,1表示。

(4) 对所得每一个层次分量求其模糊熵，得到2k个层次分量的模糊熵值，即为层次模糊熵分析，层次模糊熵可表示为：

HFE(u,k,e,m,r)=FuzzyEn(uk,e,m,r)

(9)

图1　时间序列u(i)的层次分割示意图(k=3)Fig.1　Hierarchical tree diagram of time series u(i) with k=3

综上所述，Q0和Q1算子是低频部分和高频部分，与Haar小波的低通和高通滤波的原理相一致[11]。在图1中最左侧的分解节点U1, 0,U2, 0和U3, 0的模糊熵值分别对应多尺度分析中尺度所得的模糊熵值，即分解节点Uk, 0对应多尺度分析中尺度的模糊熵值。以上分析说明多尺度模糊熵只分析时间序列低频部分的模式信息(层次模糊熵的最左侧的分解节点)，忽略了高频部分的模式信息，而层次模糊熵在分析时间序列高频部分的同时还分析低频部分的模式信息。实际测得轴承振动信号在其高频部分也存在重要的故障信息，信号低频部分的信息并不能完全反映轴承故障的本质特征，说明了对信号进行层次分析的重要性。

1.3参数选择

根据层次模糊熵的定义，在进行层次模糊熵计算前需要设置4个参数：嵌入维数m，模糊函数的相似容限r，模糊函数的边界梯度n和层次分解的层数k。(1)嵌入维数m的取值会影响动态重构时信息量的多少。m取值过小会造成重构时信息的丢失，m取值过大会有很多的详细信息，但m越大，计算所需要的数据长度N就越大(N=10m～30m)，因此综合考虑设置m=2。(2)相似容限r的取值对统计特性有影响，r过大会造成统计信息的丢失；r过小估计出的统计特性不准确。因此一般取r为0.1～0.25倍原始数据的标准差，即r=(0.1～0.25) SD。(3)模糊函数的边界梯度n在向量的相似性计算中发挥权重作用，n>1时，更多地计入较近的向量对其相似度的贡献，而更少地计入较远的向量的相似度贡献；n过大会导致细节信息的丧失，而n<1时则相反。为了获取尽量多的细节信息，根据文献[7]，取较小的整数值n=2。(4)分解层数k，k值过大会影响计算效率并且会导致参与每一个层次分量计算的点减少，同时k值过小会导致原始序列频带划分不够详细，从而不能获得足够的从低频到高频的层次分量，综合考虑取k=3。

1.4仿真数据试验

为了比较多尺度模糊熵和层次模糊熵，根据参考文献[11]定义一个白噪声信号，数据长度N=5000 如图2(a)所示，对其进行傅里叶变换和归一化处理，其结果如图2(b)所示。由图2可知，白噪声信号在各个频带上的复杂度近乎不变。

然后用层数k=3的HFE和尺度τ=8的MFE分别求解白噪声信号的模糊熵值，同时为了观察HFE和MFE算法的稳定性，在每一个尺度上分别求取100组独立白噪声的熵值的误差棒如图3所示。

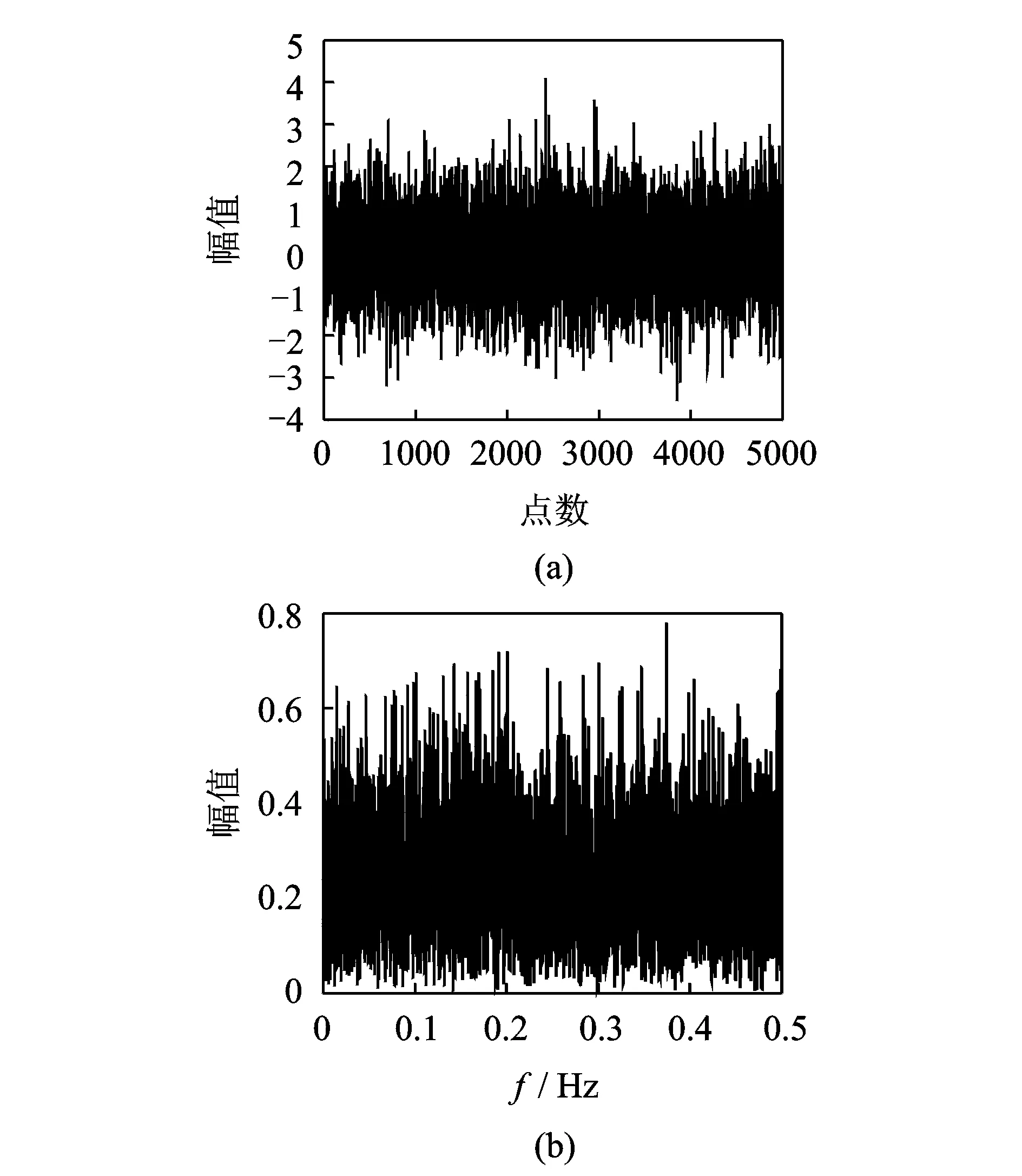
图2　白噪声的时域波形和频谱图Fig.2　Waveform and FT( Fourier transform) spectrum of white noise

图3　白噪声的层次模糊熵和多尺度模糊熵 Fig.3　HFE and MFE curves of white noise

由图3可以看出，对于白噪声信号，由HFE计算得出的层次熵值随分解节点的变化平稳，熵值变化近似独立于节点的变化, 此现象与不同频带上白噪声的熵值近似不变的结论保持一致[11]。同时观察MFE计算的白噪声的模糊熵值变化，发现模糊熵值随着尺度增加单调下降，这与白噪声在各个频带复杂度近似不变结论不符。由于MFE只分析了仿真信号的低频成分，忽略其高频的成分，而HFE能同时分析信号中的低频和高频成分，因而能提取更加丰富的信息。 最后观察HFE和MFE的计算100组独立白噪声的熵值的误差棒，通过图3发现，尺度较小时HFE和MFE都具有很好稳定性，但随着尺度增大，HFE相比于MFE的误差棒更小，这说明HFE相比于MFE的稳定更好。

2　改进二叉树支持向量机(ISVM-BT)

二叉树支持向量机(ISVM-BT)识别能力主要依赖于二叉树层次结构，目前的二叉树生成算法主要有：类间样本距离[13]和类内样本分布[14]。两种算法从不同的角度描述了样本的可分性，且具有较好的推广能力。文献[15]在结合两种算法优势的基础上提出了一种新的生成二叉树层次结构的算法，理论上能够将类间样本距离较大且类内样本分布越广的类优先分离出来。

为实现上述目的，采用欧氏距离来分别描述类间样本距离和类内样本分布的情况。给定同类特征样本集合{xi，i=1，2，…，k}，类内样本距离的定义如下：

类内样本欧氏距离为

(10)

样本xi到其他类内样本的平均距离

(11)

定义类内所有样本到其他类内样本的平均距离

(12)

同理定义类间样本距离，首先给定两类样本集合{xi，i=1，2，…，k}和{yj，j=1，2，…，k}，其中xi∈类A，yj∈类B，定义类A与类B的类间样本平均距离如下：

类A与类B间的欧氏距离

(13)

计算类A样本xi对到类B各样本间的平均距离

(14)

定义类A和类B间的平均距离

(15)

将类内平均距离和类间平均距离结合起来定义类A和类B的可分性IA,B为

(16)

式中AVIxy为类A与类B的平均距离，AVx和AVy为类内样本平均距离，K为权重值。可分性IA,B表达式中含有类内样本距离和类间样本距离，因此能同时反映类A和类B的类间样本距离和类内样本分布的情况。通过调节权重系统K(K取值为[2-4，2-3，…，23，24])，可生成最优的二叉树层次结构。

ISVM-BT的计算流程图如图4所示。

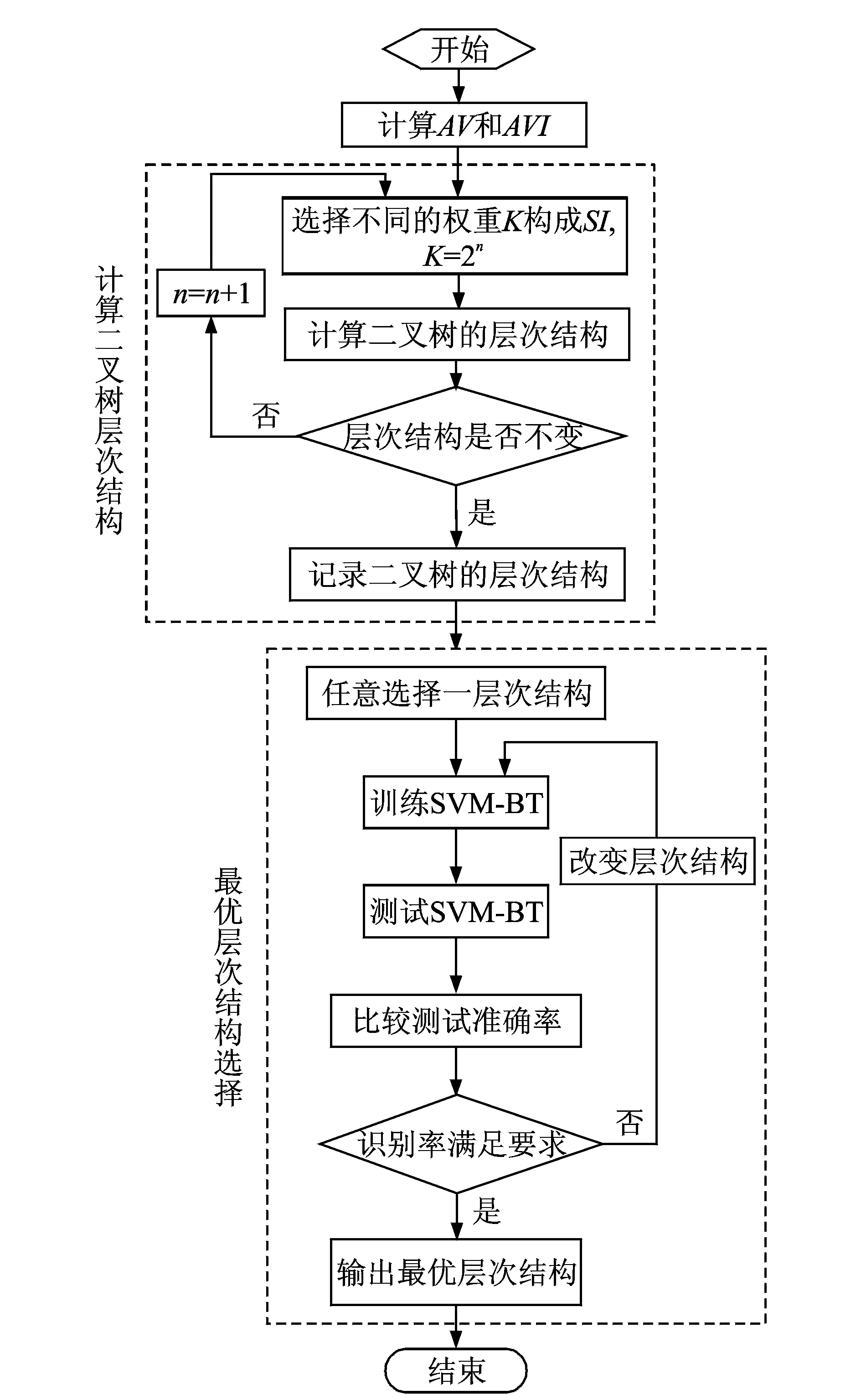
图4　ISVM-BT的计算流程Fig.4　Flowchart of ISVM-BT procedure

具体算法流程如下：

(1) 给定权值K的范围(K=2n，n=-4，-3，…，4)，计算训练样本的AV和AVI；

(2)选取某一权值K，计算当前K下的可分性矩阵SI=[Ii,j],i,j=1,2,…,N,i≠j(SI为对称矩阵)；

(17)

(3)对SI的每一行分别求和，并按值大小进行排序，若数值相等，序号小的在前；

(4)子分类器的构建：将可分性最大的类作为子分类器的第一个正类，余下的N-1类样本集合作为子分类器的负类；

(5)重复步骤(4)的过程，直至建立N-1个SVM子分类器，生成二叉树层次结构。

(6)将测试样本输入当前层次结构下支持向量机, 得出测试样本的识别准确率，并记录；

(7) 令n=n+1，得到不同的权值K，重复步骤(2)～(6)，通过最高的测试样本识别率确定最优权值K。

3　层次模糊熵和改进支持向量机的算法流程

基于层次模糊熵故障特征提取和ISVM-BT模式识别的轴承故障诊断方法流程如下：

(1)采用层次模糊熵对采集不同状态下的轴承信号进行层次k=3的模糊熵计算，得到8个节点的熵值，对每一个节点进行模糊熵计算时设置嵌入维数m=2，相似容限r=0.15*SD；

(2)将得到的8个节点熵值作为故障特征向量，同时将特征向量分为训练样本集和测试样本集；

(3)将训练样本集输入到ISVM-BT中训练，根据最高识别准确率，选出最优二叉树层次结构；

(4)将测试样本输入到由步骤(3)得到的最优二叉树层次结构中做故障模式识别。

需要注意的是经遗传算法计算的罚函数C和核函数γ会略有不同，因此以5次优化过程中最高识别率作为当前权重K值对应的识别准确率。

4　工程应用实例

4.1试验数据介绍

以美国西储大学(Case Western Reserve University)轴承实验室滚动轴承为研究对象[17]，试验台包括一个2马力电机，一个转矩传感器和一个功率计，如图5所示。本次试验采用驱动端的深沟型球轴承，其型号为6205-2RS JEM SKF。采用电火花机分别对轴承做3种故障的损伤：轴承内圈故障(IRF)，外圈故障(ORF)和滚动体故障(BF)，并做4种不同程度损伤，损伤直径分别为0.1778 mm, 0.3556 mm, 0.5334 m和0.7112 mm。振动加速度传感器固定在驱动电机支撑轴的轴承座上方，并在四种不同工况下采集振动信号。采样频率为12 kHz，采样时长为1 s，驱动电机的转速为1730 r/min，载荷为2206.50 W。

图5　轴承试验台结构简图Fig.5　The sketch of rolling bearing experiment system

4.2振动信号分析与故障特征提取

本次试验采用振动数据由3种故障状态振动信号和正常状态振动信号组成，每种故障状态又包含不同程度的故障，每种状态取60组数据，其中10组为训练样本，剩余50组为测试样本，数据长度N=2048，详细信息如表1所示。8种不同故障类型和不同故障程度的轴承故障振动加速度信号的时域波形如图6所示。

表1　试验数据列表

图6　8种不同状态下的振动信号时域波形图Fig.6　The waveforms of rolling bearing vibration signal under eight different conditions

由图6 可知，由于背景噪声干扰和故障类型较多，难以从时域波形上对不同类型和不同程度的轴承故障进行区分。首先采用MFE对不同状态下的振动数据进行处理，为了避免偶然性，每种状态下选取50组数据进行多尺度模糊熵分析，然后求均值，结果如图7所示。

图7　8种不同状态下的振动信号多尺度模糊熵Fig.7　MFE values over 8 scales for analyzing 8 health bearing conditions

由图7 可得出以下结论：首先正常状态下，滚动轴承的振动信号在大尺度上熵值较大，故障状态下熵值较小。这是由于正常滚动轴承振动信号是随机振动信号[10]，在大尺度上信号无规则性更高，自相似性较低，因此熵值较大。相比于正常状态，滚动轴承出现故障时，采集的振动信号由于受到周期性冲击，规则性增加，自相似性降低，因此熵值偏小。其次3种轴承轻度故障的多尺度模糊在大尺度上排序为：轴承外圈故障<轴承内圈故障<轴承滚动体故障。由于滚动轴承的外圈在工作时固定在基座上，不随轴旋转，出现故障时，测得振动信号自相似性最强，熵值最低；内圈是随着轴一起转动，且相比于外圈故障，内圈故障的传递路径较长，测得振动信号虽具有一定冲击性，但也具有干扰。因此相比于外圈故障，内圈故障复杂性较高，熵值较大；滚动体在随轴转动同时还有自身的转动，且传递路径最远，因此理论上滚动体故障相比于其他两种故障具有最高复杂度，熵值最大。

虽然通过多尺度模糊熵能够区分轴承正常工况和3种不同类型轻度故障工况，然而对于同一故障类型不同故障程度(如内圈轻度和中度故障)以及不同故障类型和故障程度(如内圈轻度故障、外圈中度故障和滚动体轻度故障)的故障信号，采用多尺度模糊熵进行计算时，在每个尺度上，模糊熵值很接近不能进行有效区分。

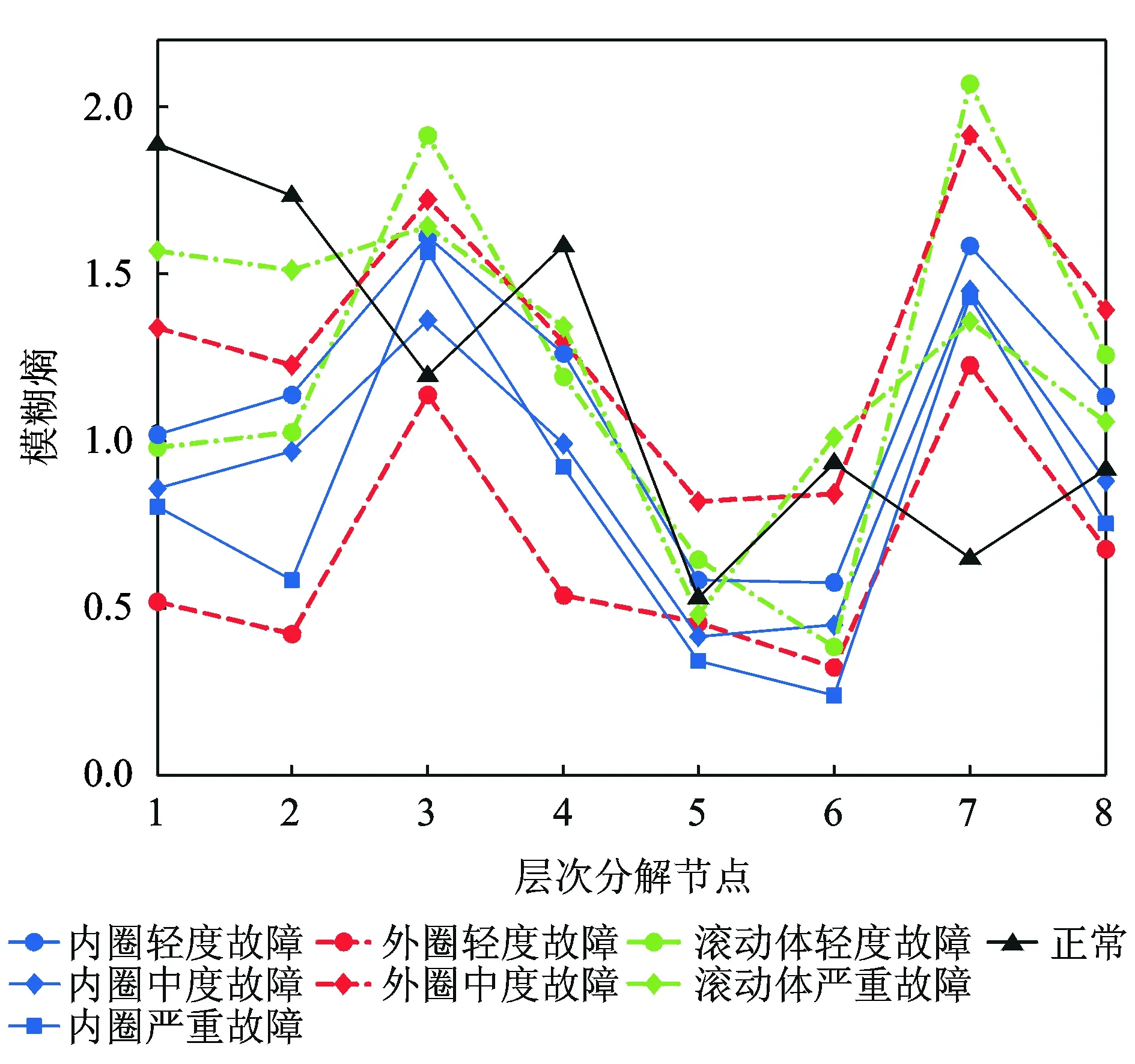
图8　8种不同状态下的振动信号层次模糊熵Fig.8　HFE values of the 8 hierarchical decomposition nodes for analyzing 8 health bearing conditions

针对多尺度模糊熵在分析轴承不同故障类型和程度存在的不足，提出了采用多层次模糊熵进行轴承故障特征的提取，设置分割层数k=3，轴承在不同状态下层次模糊熵曲线如图8所示。由图8可得出如下结论。首先轴承正常状态的层次模糊熵值随分解节点数增加呈单调下降趋势，说明振动信号的低频成分包含主要的时间模式信息。其次当轴承处于故障状态时，振动信号在低频部分(节点=3)和高频部分(节点=7)熵值较大，说明故障信息不仅隐藏在振动信号的低频部分，振动信号的高频部分也包含重要的故障信息。第三每种状态下选取50组数据进行层次模糊熵分析，每一个分解节点处的不同状态模糊熵值排序保持不变，说明层次模糊熵分析具有很好的稳定性。

综上所述，滚动轴承的振动信号的高频部分也包含重要的故障信息，只考虑低频部分的信息不能完全刻画轴承故障的本质，从而验证了层次模糊熵的优越性，适合进行轴承故障特征的提取。

4.3轴承故障诊断与结果分析

通过4.2节的分析，利用层次模糊熵提取轴承的故障特征。选取4.2节中8种工况各60组特征向量作为样本集，其中以每种工况10 样本作为训练样本，剩余50组为测试样本。权重K的取值范围设为[2-4，2-3，…，23，24]，对于每一个K值对应的二叉树层次结构，采用LibSVM工具箱对剩余的50组样本进行测试，得出在各个权值K下识别准确率，识别结果如表2所示。从表2中可以看出K=21时，识别率达到100%，从而确定出最优二叉树层次结构如图9所示。注：N 表示正常工况；I1, I2, I3表示内圈的轻度，中度和严重故障；O1, O2表示外圈的轻度和中度故障；B1, B2表示滚动体的轻度和重度故障。

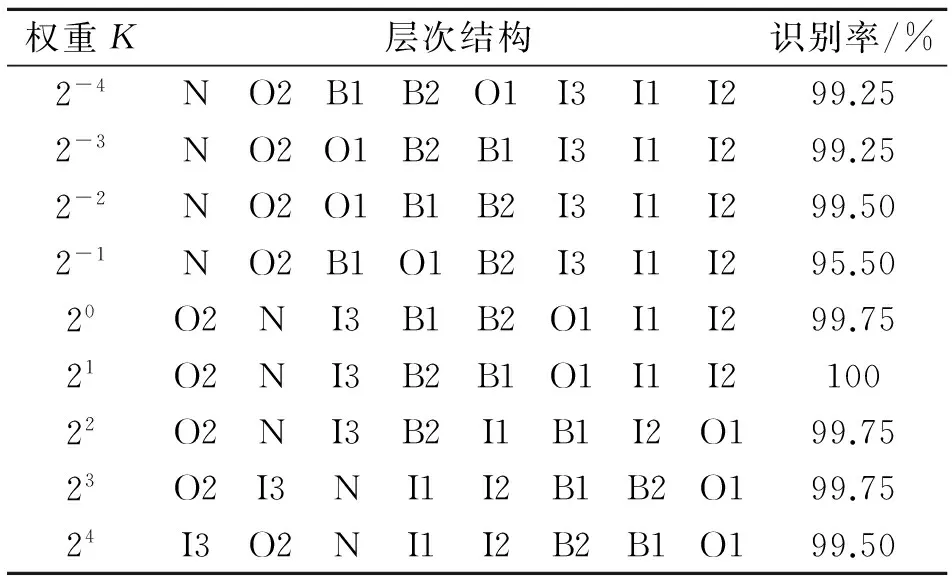
表2　不同权重值K下的层次结构和识别准确率

图9　最优层次结构下子分类器示意图Fig.9　The order of multi-fault classifier under optimum hierarchy structure

为了评价ISVM-BT的识别性能，与单独的类间样本距离法(Inter-BT)类内样本分布法(Intra-BT)进行对比，识别结果如表3所示。从表3可知ISVM-BT具有高的识别率，验证了其识别性能的优越性。

为了验证层次模糊熵在故障特征提取能力上的优越性，采用多尺度模糊熵对相同样本进行计算，为了使得输入特征向量维数与层次模糊熵保持一致，设置尺度, 采用相同步骤对多尺度模糊熵进行模式识别，K取2-1对应最高识别率为98.75%，共出现5个测试样本被误分。其中3个内圈轻度故障错分为滚动体轻度故障, 2个外圈中度故障错分为内圈轻度故障，与上述的理论分析一致。

表3　3种不同分类器下的层次结构和识别准确率

同时为进一步说明层次模糊熵的优越性，将其与小波包分解的方法进行对比。为了保证两种方法在输入特征向量维数上的一致性，使用3层小波包分解[18]。小波包分解的方法如下：首先对轴承振动信号进行小波包分解，然后计算各频带分量的模糊熵值作为特征向量，最后输入ISVM-BT进行模式识别。当K=20对应最高识别率为99.25%，出现3个测试样本被误分。其中2个轴承内圈轻度故障错分为内圈中度故障和1个滚动体轻度故障错分为内圈轻度故障。对比结果进一步验证了层次模糊熵能有效提取故障特征，实现轴承不同故障类型和故障程度的诊断。同时对层次模糊熵和小波包分解的方法在计算效率方面进行对比。采用长度N=2018的轴承振动信号作为测试信号，分别采用两种方法进行求解。层次模糊熵的计算时间为2.16 s，而小波包分解方法的计算时间为50.42 s，结果表明层次模糊熵在计算效率上优于小波包分解的方法。

为避免采用单一分类器出现的偶然性，本文采用一对一方法(OAO)[19]、一对多方法(OAA)[20]、Inter-BT方法 和Intra-BT方法等不同多分类器分别对层次模糊熵法和多尺度模糊熵法进行模式识别，识别结果如表4所示。由表4可得出以下结论：首先在每种多分类器下，相比于多尺度模糊熵，层次模糊熵都拥有较高的识别准确率，排除了单一分类器识别准确率高的偶然性，进一步验证了层次模糊熵能够更全面、更深刻的提取轴承故障信息。其次相比于其他多分类器，ISVM-BT对于层次模糊熵和多尺度模糊熵都具有最高识别准确率，也说明了ISVM-BT在识别能力上具有优越性。

表4　基于HFE和MFE的最优参数和诊断结果

5　结　论

(1)在模糊熵的基础上，结合层次分析思想提出一种新的特征提取方法——层次模糊熵。与多尺度模糊熵相比，层次模糊熵同时分析信号中的低频分量和高频分量的故障信息，对故障特征描述更加全面。

(2)给出了层次模糊熵的算法步骤，并利用仿真信号验证了该算法的优越性。

(3)基于层次模糊熵提取滚动轴承的故障特征，应用ISVM-BT实现了轴承不同故障类型和故障程度的准确诊断，为轴承故障诊断提供了一种新思路。

[1]李辉，郑海起，杨绍普. 基于EMD和Teager能量算子的轴承故障诊断研究[J]. 振动与冲击，2008，27(10)：15—17,22.

Li Hui,Zheng Haiqi,Yang Shaopu. Bearing fault diagnosis based on emd and teager kaiser energy operator[J]. Journal of Vibration and Shock, 2008，27(10)：15—17,22.

[2]Qiu H, Lee J, Lin J, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J]. Journal of Sound and Vibration, 2006, 289: 1066—1090.

[3]张超, 陈建军, 徐亚兰. 基于 EMD 分解和奇异值差分谱理论的轴承故障诊断方法[J]. 振动工程学报, 2011, 24(5): 539—545.

Zhao Chao, Chen Jianjun, Xu Yalan. A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value[J]. Journal of Vibration Engineering, 2011, 24(5): 539—545.

[4]Pincus S M. Approximate entropy as a measure of system complexity [J]. Proceedings of the National. Academy of Sciences, 1991, 88: 2297—2301.

[5]Pincus S M. Approximate entropy as a complexity measure [J]. Chaos, 1995, 5(1): 110—117.

[6]Richman J S, Mo orman J R. Physiological time-series analysis using approximate entropy and sample entropy [J]. American Journal of Physiology-Heart Circulatory Physiology, 2000, 278: 2039—2049.

[7]陈伟婷. 基于熵的表面肌电信号特征提取研究 [D]. 上海:上海交通大学, 2008.

Chen Weiting. A study of feature extraction from SEMG signal based on entropy [D]. Shanghai: Shanghai Jiao Tong University, 2008.

[8]Costa M, Goldberger A L, Peng C K. Multiscale entropy analysis of physiologic time series [J]. Phys. Rev Lett., 2002, 89: 062102.

[9]Costa M, Goldberger A L, Peng C K. Multiscale entropy analysis of biological signals [J]. Phys. Rev. E., 2005, 71: 021906.

[10]郑近德, 陈敏均, 程军圣, 等. 多尺度模糊熵及其在滚动轴承故障诊断中的应用[J]. 振动工程学报, 2014, 27(1):145—151.

Zheng Jinde,Chen Minjun,Cheng Junsheng.Multiscale fuzzy entropy and its application in rolling bearing fault diagnosis. [J].Journal of Vibration Engineering, 2014, 27(1):145—151.

[11]Jiang Ying, Peng C K, Xu Yuesheng. Hierarchical entropy analysis for biological signals [J]. Journal of Computational and Applied Mathematics, 2011, 236:728—742.

[12]朱可恒, 宋希庚, 薛冬新. 一种基于层次熵和 SVM 的轴承故障诊断方法[J]. 噪声与振动控制, 2013, 33(6): 163—167.

Zhu Keheng, Song Xigeng, Xue Dongxin. Roller bearing fault diagnosis based on hierarchical entropy and SVM[J].Noise and Vibration Control, 2013, 33(6): 163—167.

[13]Xia Shiyu, Li Jiuxian, Xia Liangzheng, et al. Tree-structured support vector machines for multi-class classification[C]. Lecture Notes in Computer Science, Berlin, Heidelberg: Springer-Verlag, 2007,4493: 392—398.

[14]袁胜发,褚福磊.次序二叉树支持向量机多类故障诊断算法研究[J]. 振动与冲击, 2009, 28(3):51—55.

Yuan Sheng-fa, Chu Fu-lei. Multi-class fault diagnosis based on support vector machineswith sequenced binary tree archtecture[J]. Journal of Vibration and Shock, 2009, 28(3):51—55.

[15]赵海洋, 徐敏强, 王金东. 改进二叉树支持向量机及其故障诊断方法研究[J]. 振动工程学报, 2013, 26(5): 764—770.

Zhao Hai-yang, Xu Min-qiang, Wang Jin-dong. An improved binary tree SVM and application for fault diagnosis[J]. Journal of Vibration Engineering, 2013, 26(5): 764—770.

[16]Richman J S, Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000,278:H2039-H2049.

[17]Bearing Data Center, Case Western Reserve University[WB/OL]. http://csegroups.case.edu/bearingdatacenter/pages/download-data-file.

[18]赵志宏, 杨绍普. 基于小波包变换与样本熵的滚动轴承故障诊断[J]. 振动、测试与诊断, 2012, 32(4): 640—644.

Zhao Zhi-hong, Yang shao-pu. Roller bearing fault diagnosis based on wavelet packet transform and sample entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 640—644.

[19]Knerr S, Personnaz L, Dreyfus G. Single-layer learning revisited: a stepwise procedure for building and training a neural network[C]//Fogelman-Souli F, Herault J ed. Neurocomputing: Algorithms, Architectures and Applications. Springer, Berlin, 1990.

[20]Vapnik V. The Nature of Statistical Learning Theory[M]. New York: Springer, 1995.

A study on rolling bearing fault diagnosis method based on hierarchical fuzzy entropy and ISVM-BT

LIYong-bo,XUMin-qiang,ZHAOHai-yang,HUANGWen-hu

(School of Astronautics, Harbin Institute of Technology, Harbin 150080, China)

A new rolling bearing fault feature extractor called hierarchical fuzzy entropy (HFE) is proposed in this paper, which is composedcomprises the of hierarchical procedure and the fuzzy entropy calculation. Compared with multi-scale fuzzy entropy (MFE) method, HFE method considers both the low and high frequency components of the vibration signals, which can provide a much more accurate estimation of entropy. Besides, improved support vector machine based binary tree SVM (ISVM-BT) has the priority of high recognition accuracy compared with other classifiers. HenceTherefore, in this paper we proposed a novel rolling bearing fault diagnosis method based on HFE and ISVM-BT is proposed in this paper. Firstly, HFE is utilized to extract fault features and then the fault features are fed into the ISVM-BT to automatically fulfill the fault patterns identifications. The experimental results show the proposed method is effective in recognizing the different categories and severities of rolling bearings.

fault diagnosis; hierarchical fuzzy entropy (HFE); improved support vector machine based binary tree(ISVM-BT); rolling bearing

2014-09-01；

2015-04-27

国家自然科学基金资助项目(10772061)

TH165+.3

A

1004-4523(2016)01-0184-09

10.16385/j.cnki.issn.1004-4523.2016.01.023

李永波(1986—),男，博士研究生。E-mail：liyongbo0532@126.com

徐敏强(1960—)，男，博士生导师，教授。E-mail：xumq@hit.edu.cn