考虑结构尺寸效应的台风场阵风因子特性分析*

李利孝, 郑　斌, 肖仪清, 宋丽莉

(1.哈尔滨工业大学深圳研究生院， 广东 深圳 518055; 2.中国气象局公共气象服务中心， 北京 100081)



考虑结构尺寸效应的台风场阵风因子特性分析*

李利孝1, 郑斌1, 肖仪清1, 宋丽莉2

(1.哈尔滨工业大学深圳研究生院， 广东 深圳 518055; 2.中国气象局公共气象服务中心， 北京 100081)

为了克服现行固定时距阵风因子在进行结构抗风设计时潜在的不足，提出一种基于性能设计的阵风因子确定方法。首先，在极值理论所建立的阵风因子基础上，通过引入滑动平均滤波器与气动导纳函数等效的方法建立了考虑结构尺寸效应和平均风速的阵风时距确定方法；之后对常见的5种气动导纳函数进行分析得到了等效阵风时距计算公式；最后利用2006年到2008年间影响中国的三次台风过程实测数据，分别建立了A,B两类场地不同时距阵风因子曲线。研究结果表明：由Vickery通过实验测得气动导纳函数确定的等效阵风时距最大，由Newberry等实测得到的脉动风压相干函数经验式确定的等效阵风时距最小；综合五种气动导纳函数的计算结果，等效阵风时距可取为1.33倍的结构宽度与平均风速比值；随着场地粗糙度增加，阵风因子显著增大；实测台风场阵风因子大于规范给出相应场地类别推荐值。

结构抗风； 阵风因子； 阵风持时； 空间相关性； 气动导纳

引　言

基于极值风速的抗风设计是结构服役期内抗风安全性的重要保证。阵风因子是预测参考时间尺度内极值风速的主要参量，定义为时间尺度T内持时τ的最大阵风与平均风速的比值。目前国内外现行抗风设计规范的阵风因子均是定义为3 s阵风风速(澳大利亚规范现采用0.2 s阵风)与10 min或1 h平均风速的比值[1]。然而，阵风持时τ的选取一直无明确定论，目前国际上较为通用的3 s持时与早期广泛使用的Dines风速仪响应特性有关[2]。Newberry[3],Vickery[4],Holmes[2, 5]和Greenway[6]等曾对阵风持时选取进行过细致的分析。

阵风因子的取值除了受阵风持时τ以及参考时距T的影响外，还与下垫面粗糙度程度、离地高度、大气层结稳定度以及天气系统类型等有密切关系[7]。Durst[8]最早给出不同时距τ阵风因子的变化关系；Krayer和Marshall[9]根据1979到1989年的四次飓风过程得到了飓风情况下的阵风因子曲线，发现在不同时距τ下的阵风因子值较Durst的研究结果(基于非气旋风场实测结果)大；Vickery[10]分析了飓风条件下在海洋下垫面和陆地下垫面的阵风因子，并与非气旋风场下阵风因子理论值进行了对比，认为飓风和非气旋风场内的阵风因子比较接近，飓风场中较大的阵风因子是源于对流湍流的贡献，但属于小概率事件；Wang[11]和Yu等[12]分别基于实测的若干次台风过程对不同下垫面的阵风因子做了系统研究。然而，这些对阵风因子的研究均未将风场自身的空间相关特性以及结构本身的尺寸因素等考虑进去。

本文将通过引入滑动平均滤波器与气动导纳函数等效的方法建立考虑结构尺寸效应与平均风速的阵风时距确定模型；并利用近年来影响中国沿海的几次典型台风过程中获取的风速记录得到中国《建筑结构荷载规范》定义的A类和B类场地类别台风风场的阵风因子曲线，从而建立完整的阵风因子确定方法，以期为台风影响区结构抗风设计提供借鉴参考。

1　考虑结构尺寸效应的阵风持时分析

1.1等效原理介绍

大气边界层风可看成许多大小不同尺度的漩涡叠加而成，当漩涡尺度较大时，同一漩涡内结构物表面各点风荷载具有较好的同步性从而易引起极值荷载[6]。阵风因子代表的阵风亦是表征了一种特定尺度的涡漩结构。为了更加准确地估计结构受到的极值风荷载，阵风因子的计算应当能够反映风场空间相关性的影响。本文采用了由Newberry[3]最先提出并被Holmes[5]进一步完善的方法来等效考虑阵风的空间相关特性。

时间尺度T内持时τ的阵风因子可表示为

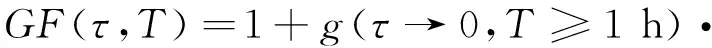
(1)

式中g(τ,T)和σ(τ,T)分别为时间尺度T内持时τ的脉动风速的峰值因子和标准差；TIu=σu(T)/U(T)为参考时距T内纵向脉动风速湍流强度，U(T)为平均风速。

基于Davenport[13]极值穿越理论，对平稳高斯随机过程，峰值因子g(τ,T)可表示为

(2)

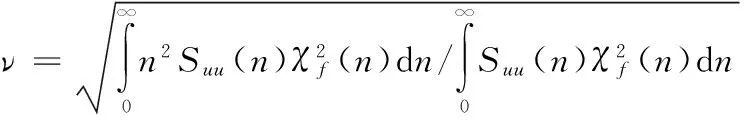
(3)

式中λ为风速仪的距离常数。

式(1)中σu(τ,T)/σu(T)用于考虑σu(τ,T)与σu(T)之间的差别，对于平稳随机过程可通过以下公式计算

(4)

(5)

式中B为结构迎风面宽度；H为结构迎风面高度;Coh(n,r)为脉动风速相干函数，定义为

(6)

式中Su1u2(x1,z1;x2,z2;n)为迎风面上任意两点(x1,z1)和(x2,z2)的纵向脉动风速互功率谱密度函数；Su1u1(x1,z1;n)和Su2u2(x2,z2;n)分别为两点的纵向脉动风速自功率谱密度函数

为便于工程借鉴，在本文的分析过程中主要考虑水平方向相关，式(5)则简化为

(7)

气动导纳函数在频域内描述了结构物表面风荷载的空间相关性对结构整体风荷载的影响，与式(3)所表示的滤波器函数具有相似的物理意义，因此可以通过构造具有相同滤波效果的气动导纳函数(7)对滤波器函数(3)进行替换[5]，从而在基于阵风因子值不变的前提下，建立阵风时距τ的等效计算模型。

1.2等效阵风持时模型

1.2.1气动导纳函数介绍

气动导纳函数可直接通过实验测量得到，亦可通过公式(7)经相干函数积分计算，本文所分析的几种气动导纳函数为：

(1)Vickery模型(V65)

Vickery[15]通过对圆形、矩形等不同几何形状和尺寸的平板进行气动导纳实验，得出了较为通用的平板气动导纳函数

(8)

式中A为平板面积；U为平均风速。

(2)Newberry模型(N73)

脉动风压相干函数的经验表达式为

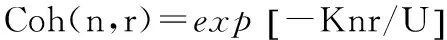
(9)

式中ρ为空间两点距离；K为衰减系数，根据Lawson[16]和Newberry[17]的全尺寸实验结果，建议取K=4.5。

(3)Davenport模型(D66)

Davenport[18]提出如下脉动风速水平向和竖向相干函数：

(10)

(11)

式中Cx=8，Cz=7。

当结构竖向和水平向尺寸均较大时，需同时考虑两个方向的相关性，可采用下式计算

Coh(r,n)=

(12)

(4)Shiotani模型(S67)

Shiotani[19]在实验的基础上建议相干函数为空间两点距离的函数，其一直被中国《建筑结构荷载规范》(GB50009-2012)所采用，即

(13)

式中Lz=50，Lx=60。

(5)Krenk模型(K96)

为了解决相干函数在垂直于平均风速的平面上积分不为零以及当频率取零时空间两点相干函数恒等于1的问题，Krenk[20]提出了修正的脉动风速相干函数：

(14)

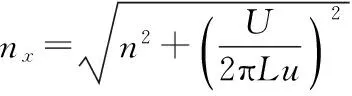
根据上述5种不同模型可以分别得到在不同平均风速和结构物宽度时所对应的气动导纳函数，为直观说明，在图1中给出了结构宽度B=20 m，平均风速U=10 m/s时5种气动导纳函数的对比图作为示意。可以看到，S67模型确定的气动导纳函数与频率项无关。

图1　气动导纳函数对比(B=20 m，U=10 m/s)Fig.1　Comparison of aerodynamic admittance (B=20 m, U=10 m/s)

1.2.2等效阵风持时确定

(15)

另外，由于S67模型和K96模型无法得到等效阵风时距的显式表达，本文采用数值计算并拟合的方法进行确定。经过上述方法的计算和拟合，分别得到5种气动导纳函数对应的阵风时距系数，汇总于表 1。其中阵风持时与结构宽度以及平均风速的关系采用下式进行表达

(16)

式中K为待定系数。

由表1可见V65模型计算得阵风持时系数最大,而由N73模型计算得阵风持时系数最小，其他3种阵风时距系数均比较接近。在本文选用上述5种模型的平均值作为等效阵风持时系数，于是得

(17)

上述5种气动导纳函数所对应的等效阵风持时曲线以及式(17)绘于图 2。由等效阵风时距公式(17)可得，在平均风速U相同的情况下，结构尺寸B越大，将其完全包裹所需要的漩涡尺度也就越大，因此需要的阵风持时τ越长。

图2　等效阵风持时曲线Fig.2　Equivalenct gusty duration

计算模型相干函数气动导纳系数KV65/χ2(n)=11+2nBU()43{}21.722N73Coh(n,r)=exp-KnrU(){}χ2(n)=49x()+881x2()exp(-4.5x)-1[]x=nBU0.780D66Coh(n,r)=exp(-8nrU)χ2(n)=14x()+132x2()exp(-8x)-1[]x=nBU1.387S67Coh(r)=exp-rLz()χ2(n)=-5000+5000exp-150B()+100BB21.232K96Coh(n,r)=1-nxCxr2U[]·exp-nxCxrU(),其中nx=n2+U2πLu()2无显式表达式1.517

2　基于近地实测的台风场阵风因子

2.1数据来源及样本选取

为了得到能够反映中国台风影响区的阵风因子曲线供结构设计参考，本文选取了2006年第1号台风珍珠(Chanchu)、2008年第12号台风鹦鹉(Nuri)以及第14号强台风黑格比(Hagupit)三次台风过程中的现场实测数据进行分析。台风珍珠的观测地点为红海湾观测站(RBT，经纬度分别为115.5734E, 22.7337N)；台风鹦鹉的观测地点包括三角岛测风塔(DIT，经纬度113.7096E, 22.1413N)以及香港天文台(HKO)在香港机场观测站实测数据；台风黑格比的观测地点为吴阳镇沙角旋海边测风塔(ST，经纬度110.6541E, 21.2538N)。各测站使用的风速仪类型以及安置高度等具体信息如表2所示。

本文选取的样本10 min平均风速除香港机场观测站为大于10.8 m/s外，其余观测站均大于17.2 m/s，以满足中性层结假定。为了避免非平稳性的影响，对各样本进行去除趋势项处理并使用逆序法和轮次检验法进行非平稳性检验，仅选取同时满足以上两种检验方法的平稳样本用于后续分析。所选样本的基本信息如表2所示。

2.2粗糙度长度计算及分类

粗糙度长度表征了下垫面与大气边界层间的相互作用。阵风因子的大小受下垫面粗糙度、平均风速、离地高度、大气稳定度以及天气系统等多种因素的影响，其中对下垫面粗糙度极为敏感，本文将按粗糙度长度对样本进行分类。

由于下垫面为水面时粗糙度长度受到平均风速的影响，在本文采用使用修正的Charnock模型[21]进行迭代计算，具体计算公式如下：

(18)

表2　测站及风速样本汇总表

(19)

(20)

(21)

式中u*为摩擦速度；g为重力加速度；ρ为空气密度；τ为切应力；Cd为拖曳系数；ν为空气的运动黏性系数；α为Charnock常数，采用如下确定方法如下：

(22)

式中δ和γ为待定参数，参照文献[21]取δ=1.0，γ=0.6。

当下垫面为陆地时，粗糙度长度采用湍流强度法计算

z0=exp(lnz-κ·TR/TIu)

(23)

式中κ=0.4为von Karman常数；TIu为湍流强度；z为离地高度；TR=σu/u*为湍流比，为保持一致，此处统一取2.79[22]。

按上述方法完成下垫面粗糙度长度计算后参照美国荷载规范ASCE-7-10标准对样本进行场地类别划分，得到相当于中国A类场地(对应ASCE-7-10中D类)样本243个，B类场地(对应ASCE-7-10中C类)样本118个，C类场地(对应ASCE-7-10中B类)样本3个，具体信息如表 3所示。

表3　粗糙度分类结果

2.3阵风因子曲线

基于实测数据，通过滑动平均的方法计算了样本数量较多的A类和B类两类场地下各样本在阵风持时从1 s到600 s的阵风因子，并采用分位数统计法得到对应的阵风因子曲线；由于C类场地样本数量过少，所以在本文将不展开分析。计算得到中国规范A类和B类场地的阵风因子统计特征曲线(包括上四分位数、中位数和下四分位数曲线)分别如图 3(a)和(b)所示。其中中位数反应了样本阵风因子的平均水平，而上下四分位数则反应了样本偏离平均水平的程度。

对比图3(a)和(b)可见，阵风因子对下垫面粗糙度类别比较敏感，场地越粗糙，阵风因子值越大；随着阵风时距的减小，两类场地的阵风因子均不断增大，而且场地越粗糙增大速度越快。B类场地在1，3和10 s阵风持时的阵风因子平均值分别为1.545,1.478和1.353，在A类场地1，3和10 s阵风因子平均值分别为1.326,1.292和1.213。中国《建筑结构荷载规范》间接给出A类和B类场地的10 m高度的阵风因子分别为1.265和1.304，均小于台风场实测值。

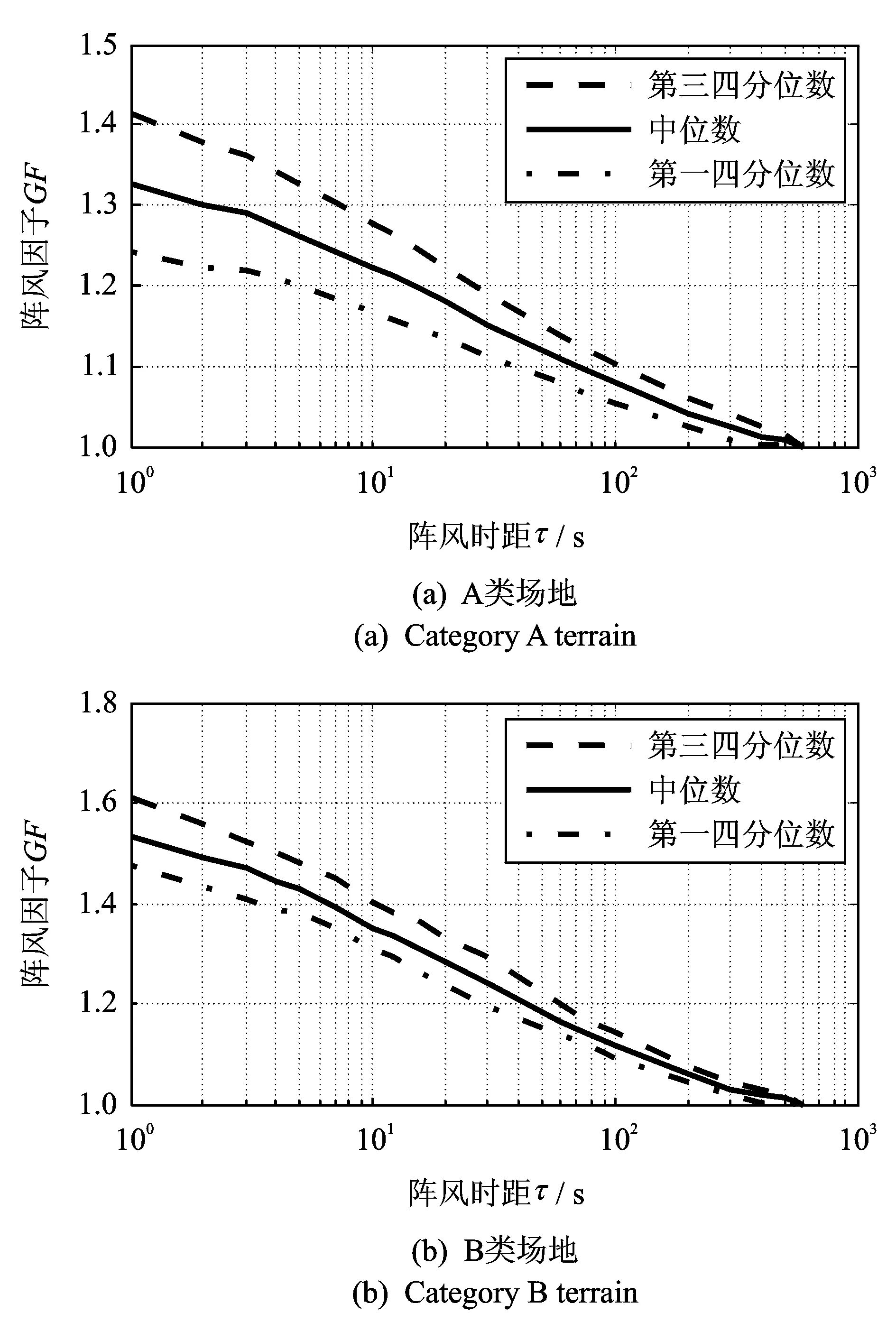
图3　阵风因子曲线(τ=1～600 s)Fig.3　Gust factor (τ=1～600 s)

至此，本文建立了完整的台风影响区阵风因子确定模型。在结构设计时，根据结构特征尺度和设计基准风速依据等效阵风持时公式(17)确定相应的阵风持时，然后基于不同阵风持时阵风因子图(图3)确定对应场地类别下的阵风因子取值。使用本文模型建立的阵风因子充分考虑了风荷载的空间相关性对不同尺度结构的作用，比固定持时阵风因子更符合实际。

3　结　论

本文在极值理论建立的阵风因子基础上，通过引入滑动平均滤波器与气动导纳函数等效的方法建立了考虑结构尺寸效应的等效阵风持时确定方法，并利用影响中国的三次台风过程近地实测数据计算了两类不同场地下的阵风因子曲线，得到以下主要结论：

(1)结构设计中确定阵风持时时，应考虑结构尺寸效应和平均风速的影响。

(2)利用五种气动导纳函数计算结果的平均值等效得阵风时距为结构物宽度与平均风速比值的1.33倍。阵风因子随着场地粗糙度增加显著增大；随着阵风时距的减小，两类场地的阵风因子均不断增大，而且场地越粗糙增大越快。

(3)实测台风场阵风因子大于规范给出相应场地类别推荐值。

[1]肖仪清，李利孝，宋丽莉，等. 基于近海海面观测的台风黑格比风特性研究[J]. 空气动力学学报，2012,30(3):380—387,399.

Xiao Y Q, Li L X, Song L L, et al. Study on wind characteristics of typhoon Hagupit based on offshore sea surface measurements[J]. Acta Aerodynamica Sinica， 2012,30(3):380—387, 399

[2]Holmes J D, Ginger J D. The gust wind speed duration in AS/NZS 1170.2[J]. Australian Journal of Structural Engineering, 2012, 13: 207—216.

[3]Newberry C W, Eaton K J, Mayne J R. The Nature of Gust Loading on Tall Buildings[M]. Building Research Station, 1968.

[4]Vickery B J. On the flow behind a coarse grid and its use as a model of atmospheric turbulence in studies related to wind loads on buildings[J]. Nat. Phys. Lab. Aero. Report, 1965, 1143.

[5]Holmes J D. Equivalent time averaging in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72: 411—419.

[6]Greenway M E. An analytical approach to wind velocity gust factors[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1979, 5(1—2): 61—91.

[7]陈雯超，宋丽莉，植石群，等. 不同下垫面的热带气旋强风阵风系数研究[J]. 中国科学: 技术科学, 2011, 41(11): 1449—1459.

Chen W C, Song L L, Zhi S Q, et al. Analysis on gust factor of tropical cyclone strong wind over different underlying surfaces[J]. Sci China Tech Sci., 2011, 54: 2576—2586.

[8]Durst C S. Wind speeds over short periods of time[J]. Meteor. Mag., 1960, 89: 181—187.

[9]Krayer W R, Marshall R D. Gust factors applied to hurricane winds.[J]. Bulletin of the American Meteorological Society, 1992, 73: 613—618.

[10]Vickery P J, Skerlj P F. Hurricane gust factors revisited[J]. Journal of Structural Engineering, 2005, 131(5): 825—832.

[11]Wang B, Hu F, Cheng X. Wind gust and turbulence statistics of typhoons in South China[J]. Acta Meteorologica Sinica, 2011, 25: 113—127.

[12]Yu B, Gan Chowdhury A. Gust factors and turbulence intensities for the tropical cyclone environment[J]. Journal of Applied Meteorology and Climatology, 2009, 48(3): 534—552.

[13]Davenport A G. Note on the distribution of the largest value of a random function with application to gust loading[C]. Ice Virtual Library, 1964.

[14]Beljaars A. The influence of sampling and filtering on measured wind gusts[J]. Journal of Atmospheric and Oceanic Technology, 1987, 4(4): 613—626.

[15]Vickery B J. On the flow behind a coarse grid and its use as a model of atmospheric turbulence in studies related to wind loads on buildings[J]. Nat. Phys. Lab. Aero. Report., 1965, 1143.

[16]Lawson T V. The design of cladding[J]. Building and Environment, 1976, 11(1): 37—38.

[17]Newberry C W. Wind Loading on Tall Buildings: Further Results from Royex House[M]. Building Research Establishment, 1973.

[18]Davenport A G. The relationship of wind structure to wind loading[C]. The International Conference on the Wind Effects on Buildings and Structures, Teddington, Middlesex : National Physical Laboratory, 1963:54—102.

[19]Shiotani M, Arai H. Lateral structures of gusts in high winds[C]. Proceedings of the International Conference on Wind Effects on Buildings and Structures, Ottawa, 1967:535—555.

[20]Krenk S. Wind field coherence and dynamic wind forces[C]. Proceedings of the IUTAM Symposium held in Trondheim, Norway, 1995:269—278.

[21]Zeng Z, Wang Y, Duan Y, et al. On sea surface roughness parameterization and its effect on tropical cyclone structure and intensity[J]. Advances in Atmospheric Sciences, 2010, 27(2): 337.

[22]Deaves D M. Terrain-dependence of longitudinal RMS velocities in the neutral atmosphere[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 8(3): 259—274.

Characteristics of gust factors considering the structural size effect in typhoon wind field

LILi-xiao1,ZHENGBin1,XIAOYi-qing1,SONGLi-li2

(1. Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China；2. Public Meteorological Service Center, China Meteorological Administration, Beijing 100081, China)

In order to overcome the potential shortcomings of the fixed time scale gust factor used in wind-resistant design of buildings, a performance-based design approach is proposed to determine the gust factor. First, a method to determine the gust duration based on the extreme value theory, which also considers the effects of the structural size and mean wind speed, is proposed by matching the moving average filter and aerodynamic admittance. After that, five distinct sources of aerodynamic admittance are examined to deduce the gust duration. Finally, based on the field measurements of 3 typhoons from 2006 to 2008, the gust factor curves are given in category A and B. The results show that the gust duration determined by empirical aerodynamic admittance suggested by Vickery is the largest, while that determined by the coherence of wind velocity suggested by shiotani is the smallest and the average value is about 1.33 times the ratio of structural width to mean wind velocity. It also shows that the gust factor increases significantly with the increase of the roughness length, and the gust factor in typhoon wind fields are greater than the value in the corresponding terrain in 〈Load code for the design of building structures〉 of China.

wind-resistant of building; gust factor; gust duration; spatial correlation; aerodynamic admittance

2014-05-29；

2015-09-08

国家自然科学基金资助项目(51308168，51278161)；中国博士后科学基金资助项目(2013M531045,2014T70343)

TU973.3+2

A

1004-4523(2016)01-0177-07

10.16385/j.cnki.issn.1004-4523.2016.01.022

李利孝(1984—)，男，博士后。电话:(0755)26033021，18682013431;E-mail:lilixiao1984@foxmail.com