弹性体作定轴转动的耦合动力学模型与数值分析*

郭小炜， 刘占芳， 郝志明

(1.重庆大学煤矿灾害动力学与控制国家重点实验室， 重庆 400030；2.重庆大学航空航天学院， 重庆 400030；3.中国工程物理研究院总体工程研究所， 四川 绵阳 621900)



弹性体作定轴转动的耦合动力学模型与数值分析*

郭小炜1,2， 刘占芳1,2， 郝志明3

(1.重庆大学煤矿灾害动力学与控制国家重点实验室， 重庆 400030；2.重庆大学航空航天学院， 重庆 400030；3.中国工程物理研究院总体工程研究所， 四川 绵阳 621900)

应用含偶应力的弹性理论建立弹性力学模型，应变和曲率张量分别描述弹性体的平动变形和旋转变形,且分别对应于应力和偶应力两种内力。对已知定轴变转速刚体转动的情况，采用哈密尔顿原理建立了含偶应力弹性体作定轴刚体转动的运动与变形耦合动力学模型，模型计及了相对惯性力、离心力、科氏力和切向惯性力。考虑以弹性体的位移和变形转角为独立变量，利用约束变分原理建立了含偶应力弹性体作定轴刚体转动的有限元方程，其中单元离散采用8个节点48个自由度的三维六面体实体等参元。以绕定轴旋转的悬臂梁为例，数值分析了旋转悬臂梁的动力学特性和动力学响应。当幅值变化但刚体转速恒定时，旋转方梁的一阶特征频率出现随转速增加保持不变和下降两种情况。当刚体变转速时，考察了旋转悬臂梁位移、变形转角、动态应力以及偶应力的时变规律。该研究可为作定轴旋转系统的结构部件的动力学分析提供理论模型和数值分析方法。

偶应力弹性理论；刚-柔耦合； 运动与变形耦合模型； 惯性力效应； 约束变分原理

引　言

刚柔耦合系统的动力学分析在航空航天、机器人和高速旋转机构等领域具有重要的理论和工程应用价值。譬如直升机旋翼、卫星天线、太阳能帆板和大型涡轮机叶片等，这类系统的运动变量既有大范围的刚体转动，又有小幅度的弹性变形，二者产生运动学耦合。国内外许多学者[1-16]对这种大范围运动的柔性结构动力学问题进行了长期研究，这些研究主要集中在柔性结构的大范围运动与其自身变形的耦合问题上，提出了刚柔耦合动力学模型，特别考虑了柔性结构的初应力效应以及几何非线性影响的动力刚化效应问题。洪嘉振[3-6]等基于柔性梁的小变形假设，得到了梁的一次近似刚柔耦合动力学模型，该模型相比传统的零次近似耦合模型更适用于大范围运动速度较高的情形，但随着柔性部件尺寸的增大或者结构材料柔度的增加，这个模型得出的结果与实际情况会出现较大误差。文献[3]提出了考虑非线性耦合变形量高阶项的高次耦合动力学模型，未提及高次耦合模型与一次近似耦合模型的具体差异以及高次耦合模型能否适应大变形问题。文献[12]建立了考虑耦合变形量高阶项的大范围旋转柔性梁的完整动力学模型，指出当柔性梁变形或者变形速度较大时一次近似耦合模型将出现数值发散的情况，而完整耦合模型的计算结果则依然收敛。

传统刚柔耦合动力学模型针对如板梁[7-8,14]等具体结构型式，能够获得结构的动力特性和位移响应，但不能给出应力应变的响应。就旋转结构而言，动应力状态对判断应用几何非线性或物理非线性是关键的控制变量，例如结构是否达到了屈服应力状态。为了能够同时考虑旋转结构的动力学特性和包括位移、应力应变等动力学响应，本文考察任意弹性体作刚体转动的耦合动力学问题。

弹性力学理论的重要进展是提出了含偶应力的弹性力学理论。偶应力弹性力学[17-20]的理论基础是在应变张量的基础上引入曲率张量，应变描述了平动变形，曲率张量即旋转矢量之梯度则描述了旋转变形。在材料本构关系方面，相比经典弹性力学的广义胡克定律，必须增加偶应力与曲率张量的本构关系。偶应力弹性理论已在弹性体孔周应力集中系数[21]、裂纹扩展及微结构[22-23]等静力学分析中得到了较多应用。偶应力弹性理论一个重要特点是能够考虑结构的尺寸效应，对于具有强烈尺度效应的微机电系统的发展具有重要价值，已有研究[16]对刚体-微梁系统的刚柔耦合动力学特性进行了研究，在微观尺寸下，基于偶应力弹性理论得出的结果与未考虑旋转梯度效应的经典弹性理论有较大差异。

本文采用含偶应力的弹性理论描述任意弹性体的力学行为，利用哈密尔顿(Hamilton)原理[24]建立弹性体绕定轴作变速刚体转动的耦合动力学模型。应用约束变分原理，以位移和变形转角为独立变量，构造了8结点48自由度的六面体等参元，建立了弹性体作定轴变转速刚体运动的动力学分析有限元方程。以作定轴变速旋转的空间悬臂梁为例开展了动力特性和动力学响应的数值分析，考察了旋转梁的旋转变形和作用于旋转梁的惯性力的动力学影响。

1　含偶应力弹性体作刚体转动的耦合动力学模型

考虑旋转变形的弹性体，弹性体的变形由平动变形和旋转变形合成。在小变形条件下，位移梯度分解为应变张量和旋转张量之和

(1)

其中应变张量和旋转张量

(2)

(3)

旋转张量Ω为二阶反对称张量，与其等价的旋转矢量ϖ为

(4)

(5)

所以曲率张量是旋转矢量的梯度。

弹性体的总应力是对称应力和反对称应力之和，而反对称应力联系着偶应力。对称应力与应变张量的本构关系满足广义胡克定律，偶应力m和曲率张量χ的本构关系则表达了关于旋转变形的内力与变形特性，两个本构关系[25]改成为

(6)

式中λ，μ为拉梅参数，η为旋转模量。

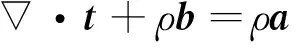
(7)

(8)

式中t=σ+τ为作用于弹性体质点上的非对称应力，a为弹性体质点的加速度。含偶应力弹性体满足边界条件：

(9)

(10)

在偶应力弹性理论中，弹性体质点上同时作用着非对称的应力和偶应力，分别对应着平动变形和旋转变形，并且应力和偶应力满足动量和动量矩守恒方程。

下面考虑弹性体作定轴刚体转动的情况。建立一个固定坐标系{ei′}和一个固结在弹性体上的浮动坐标系{ei}，如图1所示。弹性体绕一定轴以角速度ω作刚体转动。

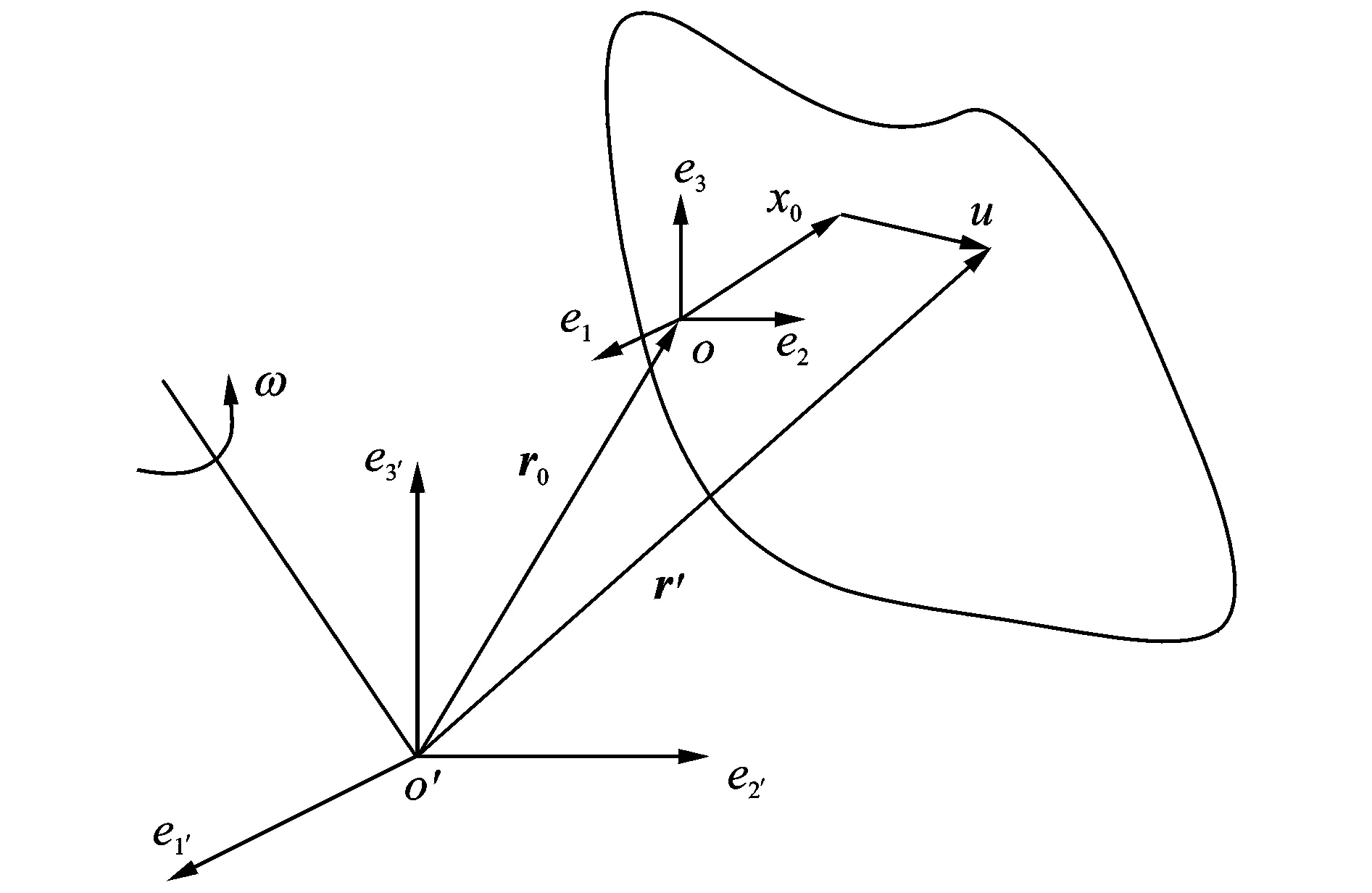
图1　绕定轴转动的弹性体及其坐标系Fig.1　The elastic body rotates about an axis

弹性体上任意一点在固定坐标系下的位置矢量为[26]

(11)

式中R为联系浮动坐标系与固定坐标系的正交张量。矢径r′为质点在固定坐标系下的位置矢量，注意矢径r0为定系原点在浮动坐标系下的位置矢量，作刚体转动时保持不变，但矢径r0在固定坐标系下由于刚体转动是变化的。矢径x0为浮动坐标系下弹性体上任意一点的初始位置。矢径u为浮动坐标系下弹性体上任意一点的位移。

Euler-Rodrigues旋转公式[27]可以表达为

(12)

(13)

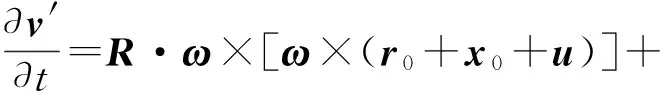
(14)

运动着的弹性体具有动能T、应变能U和外力功W。假设在瞬时t1和t2，弹性体所处的运动状态为给定的两种状态，哈密尔顿原理表达式[24]为

(15)

式中t1和t2为给定的两种运动状态的时刻，δT为系统动能的变分，δU为弹性体应变能的变分，δW为作用于弹性体上外力功的变分。

作大范围刚体转动的含偶应力弹性体，在固定坐标系下，整个系统的动能为

(16)

将式(13)代入式(16)得到

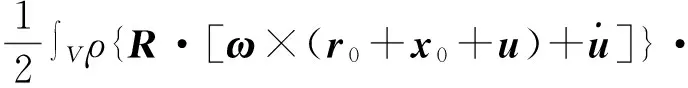
(17)

式中ρ为弹性体的密度。由正交张量的保内积性质可得系统动能T为

(18)

(19)

系统动能T的变分为

(20)

在上述的推导过程中，变分运算、积分运算与微分运算的次序可以交换。将式(20)对时间t从t1到t2进行积分，得到

(21)

由于时刻t1，t2为系统给定的两种运动状态，弹性体的位移变分为零，δu(t1)=0和δu(t2)=0，所以式(21)中第1项对时间积分，得到

(22)

同理可得式(21)中第4项为0。

注意到矢量的混合运算满足下式

(23)

对于已知刚体转动的情况，利用上式，式(21)中第3项改写为

(24)

同样注意到矢量的混合运算满足

(25)

则式(21)中第5项和第6项之和改写为

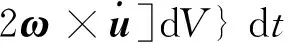
(26)

将式(24)和(26)代入式(21)得

(27)

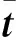
δW=∫Vρ(δu′·b′+δϖ′·c′)dV+

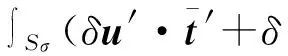
(28)

(29)

将边界条件(9)代入式(29)并利用高斯积分变换公式，可得

δW=∫V[ρ(δu·b+δϖ·c)+(δu··t+δϖ··m+t:δu+m:δϖ)]dV

(30)

将式(8)代入式(30)得

δW=∫V[δu·(·t+ρb)+(δε:σ+δχ:m)]dV

(31)

含偶应力弹性体的变形能包含质点的平动变形能和旋转变形能，在固定坐标系下，弹性体变形能U的变分为

δU=∫V(δε′:σ′+δχ′:m′)dV=

∫V(δRTεR:RTσR+δRTχR:RTmR)dV=

∫V(δε:σ+δχ:m)dV

(32)

将式(27)，(31)和(32)代入式(15)得到含偶应力弹性体的哈密尔顿方程

(r0+x0+u)}dVdt=0

(33)

使方程(33)对任意时刻t都成立，必须满足体积为V、面积为S的任意弹性体上的积分为零，即有

(34)

由于δu≠0，则上式必须满足

(

(35)

考虑到含偶应力弹性体中t=σ+τ，将式(10)代入上式，得到另一种形式的含偶应力弹性体的动力学方程

×(×c=

(36)

由方程式(35)或(36)可知，弹性体由于作刚体转动受到了离心力、切向惯性力、科氏惯性力的附加惯性力作用，造成弹性体的动力学行为发生演化。刚体转动与弹性变形发生了运动学耦合。观察发现，没有刚体转动，耦合动力学模型退化为含偶应力弹性理论，且进一步忽略弹性体旋转变形，含偶应力弹性理论退化为经典弹性力学。

2　含偶应力弹性体作刚体转动的耦合动力学方程的有限元格式

含偶应力弹性体体积为V，面积为S，取权函数为真实位移的变分δu和变形转角的变分δϖ，弹性体内力所作的虚功，作用于弹性体上外力和外力偶所作的虚功以及系统作刚体转动产生附加惯性力所作的虚功满足虚功方程

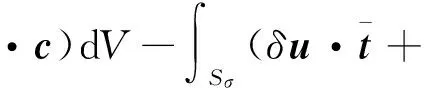
(37)

式中δε和δχ为虚应变和虚曲率张量。注意到曲率张量χ是位移的二阶导数而变形转角ϖ是位移的一阶导数，采用有限元方法进行数值分析时，为避免变形转角在节点上的非连续性，采用约束变分原理来建立有限元方程。为此，在弹性体内引入一个附加变形转角φ，该变形转角φ与由位移决定的变形转角ϖ在弹性体域内满足变分约束条件：∫Vδ(φ-ϖ)·(φ-ϖ)dV=0。对弹性体进行有限元离散时，附加变形转角φ与位移一起作为单元节点未知变量，则位移与变形转角φ均满足连续性要求。利用罚因子α将约束条件引入虚功方程，即有含偶应力弹性体作刚体转动的虚功方程(37)的约束变分形式为

α∫Vδ(φ-ϖ)·(φ-ϖ)dV=0

(38)

采用六面体8个节点48个自由度的等参元对弹性体进行离散，单元体上节点位移和变形转角均为未知变量，单元节点位移-转角列阵：

(39)

(40)

考虑到偶应力是非对称的，应力-偶应力列阵：

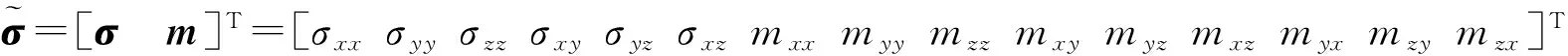
(41)

式中D1为经典的弹性矩阵，D2为偶应力与曲率张量的本构关系矩阵。其中D2=4ηI9×9，I9×9为9×9单位矩阵。

关于增加的约束项，取其变形转角差值列阵为{φ-ϖ}=[φx-ϖxφy-ϖyφz-ϖz]T，与单元节点位移-转角列阵δe存在关系

(42)

约束变分原理中出现的附加惯性力都与刚体转动速度有关。刚体转动角速度ω等价于二阶反对称张量Θ，且满足Θ=-·ω，注意以下关系式

(43)

(44)

{δδe}T(∫VeρΝTΘ′2ΝdV)δδe+

{δδe}T(α∫VeBαTBαdV)δδe={δδe}T(∫VeρΝTfdV)+

(45)

由于单元节点位移-转角变分的任意性，立即有含偶应力弹性体作刚体转动的耦合动力学模型的有限元方程

(46)

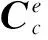
对于离散为n个单元的含偶应力弹性体，由单元有限元方程组集可得结构总体有限元方程

(47)

式中M为n个单元质量阵组集成的弹性体质量阵，C为单元科氏矩阵组集成的总体科氏矩阵，K为单元刚度矩阵、单元离心刚度矩阵、单元切向刚度矩阵和单元约束矩阵组集成的系统总体刚度阵，P为单元体力和面力列阵、单元初始离心力列阵和单元初始切向惯性力列阵组集成的弹性体广义外力列阵，δ为弹性体的位移-变形转角列阵。

3　作刚体转动悬臂梁的耦合动力学分析

利用上述有限元方程对旋转悬臂梁的动态频率、动态位移、动态应力和偶应力等进行系统分析。绕定轴转动的悬臂梁如图2所示，梁的一端固定在转动的刚性轮毂上，刚体转动的角速度为ω。固定坐标系的原点为o′。浮动坐标系的原点在旋转悬臂梁的固定端面中心，其中x轴沿着梁的展向，y轴沿刚体转动的切向，z轴与刚体转动轴一致。浮动坐标系原点与固定坐标系原点的距离r0=1.0 m，梁长L=10 m，梁横截面宽度B=0.1 m，横截面高度H=0.2 m。选取悬臂梁的材料为轧制锰黄铜，材料的弹性模量为E=110 GPa、泊松比ν=0.35、密度ρ=8.5×103kg/m3。为确定轧制锰黄铜的旋转模量，参照Fleck和Hutchinson[21]细铜丝扭转试验，铜的内禀长度约为l=4 μm，利用η=μl2得旋转模量η=0.72 Pa·m2。

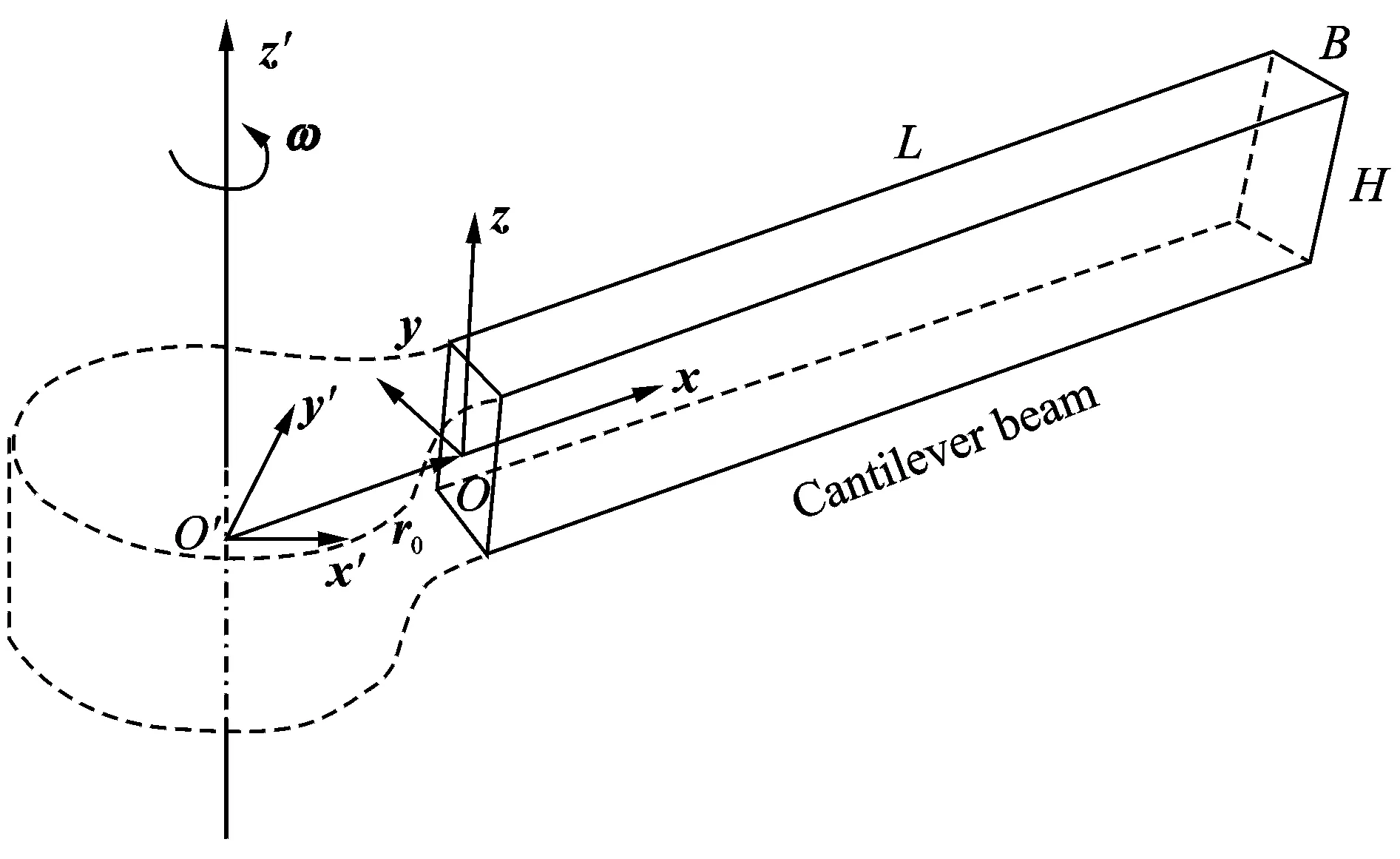
图2　绕定轴转动的悬臂梁Fig.2　The cantilever beam rotating along a fixed axis

对已知刚体转动的情况，耦合动力学方程是时变的偏微分方程组，即方程中的系数项与刚体转动的速度有关。在刚体转速恒定情况下，耦合动力学方程退化为常系数偏微分方程组，这时可考察不同恒定转速下旋转悬臂梁的特征频率。图3为旋转悬臂梁作刚体恒定转速运动但幅值不同时的第1阶特征频率。旋转悬臂方梁不作刚体转动时，其第1阶模态为悬臂梁的横向弯曲振动，即梁截面的宽度和高度两个方向，因而其相应的第1阶模态会出现两个特征频率值。从图3可以看出，旋转悬臂梁的第1阶模态对应的特征频率值会随着刚体恒定转速幅值的改变而发生漂移。第1阶模态对应的特征频率值会随着刚体恒定转速的增加保持不变和下降两种情况。旋转悬臂梁的特征频率值随着恒定转速幅值的不断增加将会逐渐下降，这里将会出现使得其特征频率趋近于零时的最大刚体恒定转速，这个最大恒定转速幅值约为2.52 rev/s，此值为旋转悬臂梁不作刚体转动时的第1阶固有频率值。由于特征频率值不能为零或者低于零，因而刚体恒定转速幅值不能超过这个值。产生这种现象的原因是由于计算模型中出现的附加惯性力项，包括相对惯性力、离心力、科氏力和切向惯性力等对旋转悬臂梁的特征频率的影响，其中离心力对其影响最为显著。

图3　不同恒定转速下旋转悬臂梁的特征频率Fig.3　Dynamic frequency of rotational cantilever beam versus varied constant rotational velocity

令已知刚体转动的角速度变化规律[1]为

(48)

式中ts为刚体转动达到恒定转速之前的加速时间，ωs为最终的恒定转速。

取加速时间为20.0 s以及最终的恒定转速为6.0 rad/s，刚体转动的角速度按照式(48)进行变化，得到图4所示的旋转悬臂梁转动角速度和角加速度随时间的变化曲线。

图4　角速度和角加速度时间历程Fig.4　Time history of the angular velocity and angular acceleration

数值计算得到了旋转悬臂梁绕定轴作刚体转动的动力学响应，包括悬臂梁的动态位移、动态变形转角、动态应力和偶应力随时间的变化曲线。图5描述了旋转悬臂梁自由端面中心点处的横向位移和变形转角随时间的变化曲线，图5(a)为浮动坐标系下旋转悬臂梁自由端面中心点处y方向的位移uy，图5(b)为悬臂梁自由端面中心点处变形转角φz，从图5可以看出，悬臂梁变形转角φz和位移uy的变化趋势一致，并且位移和转角在刚体角加速度达到最大值的时刻也达到最大值，而初始切向惯性力关联于刚体角加速度，说明初始切向惯性力对位移和变形转角的影响起着主导作用。图6为旋转悬臂梁固定端面中心的动态应力和偶应力响应曲线。动态偶应力随时间的变化趋势和变形转角随时间的变化趋势一致，主要由于偶应力取决于变形转角。动态应力既包括径向离心力对悬臂梁轴向拉伸产生的正应力又包括切向惯性力对悬臂梁横向弯曲产生的剪切应力，因而应力随时间的变化趋势与旋转悬臂梁的刚体角速度和角加速度都有关，如图6所示，达到应力峰值的时刻会延后于达到刚体角加速度最大值的时刻，此外，当悬臂梁作恒定的刚体转动时，由于离心力的作用，悬臂梁始终存在轴向正应力，而且这个值对旋转悬臂梁起着主导作用。

图5　悬臂梁自由端面中心点在浮动坐标系下的横向位移与变形转角随时间变化曲线Fig.5　Transverse displacement and the deformation angle at the free end center of cantilever beam versus time in the floating frame

图6　旋转悬臂梁固定端处的动态应力和偶应力随时间变化曲线Fig.6　Dynamic stress and couple stress at the fixed end of cantilever beam versus time in the floating frame

下面将改变旋转悬臂梁刚体转动的角速度变化规律，使角速度在加速阶段线性增加，最终达到恒定角速度，其运动规律为

(49)

同样取加速时间为20.0 s以及最终的恒定转速为6.0 rad/s，得到图7所示的旋转悬臂梁转动角速度和角加速度随时间的变化曲线。

图7　角加速度和角加速度时间历程Fig.7　Time history of the angular acceleration and angular velocity

图8描述了旋转悬臂梁在作刚体恒定角加速度时自由端面中心点处的横向位移和变形转角随时间的变化曲线，图8(a)为浮动坐标系下旋转悬臂梁自由端面中心点处y方向的位移uy，图8(b)为自由端面中心点处变形转角φz。从图(8)中可以看出，旋转悬臂梁的动态位移和变形转角的响应，在角速度恒加速阶段，位移和变形转角会发生振荡，同时位移和变形转角振动的平衡点会出现跳跃随着角加速度的突然消失，然后在恒定角速度阶段作周期性的振动。

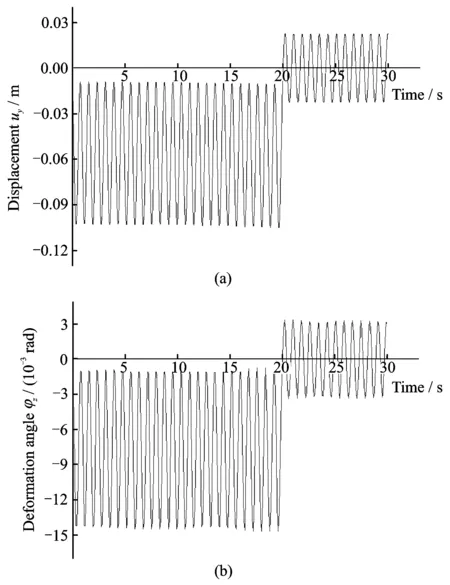
图8　悬臂梁自由端面中心点在浮动坐标系下的横向位移与变形转角随时间变化曲线Fig.8　Transverse displacement and the deformation angle at the free end center of cantilever beam versus time in the floating frame

图9为旋转悬臂梁固定端面中心的动态应力和偶应力响应曲线。如图9(a)所示，动态应力和偶应力的响应在角速度恒定加速阶段同样会出现振荡，并且应力幅值会随着角速度的增大而增大，当角加速度降为零时，应力平衡点会出现跳跃，在旋转悬臂梁恒定角速度转动时，应力将随时间呈周期性变化。图9(b)为偶应力响应曲线，由于恒定角速度时变形转角很小，而偶应力与变形转角直接相关，因而偶应力在恒定角速度阶段将会在零点附近作微小振动。角速度作线性增加的刚体转动，旋转悬臂梁的位移、变形转角、应力和偶应力的响应会出现振荡，这与旋转悬臂梁作连续的变角加速度转动时的响应不同，产生这种现象的原因将在下面结论中讨论。

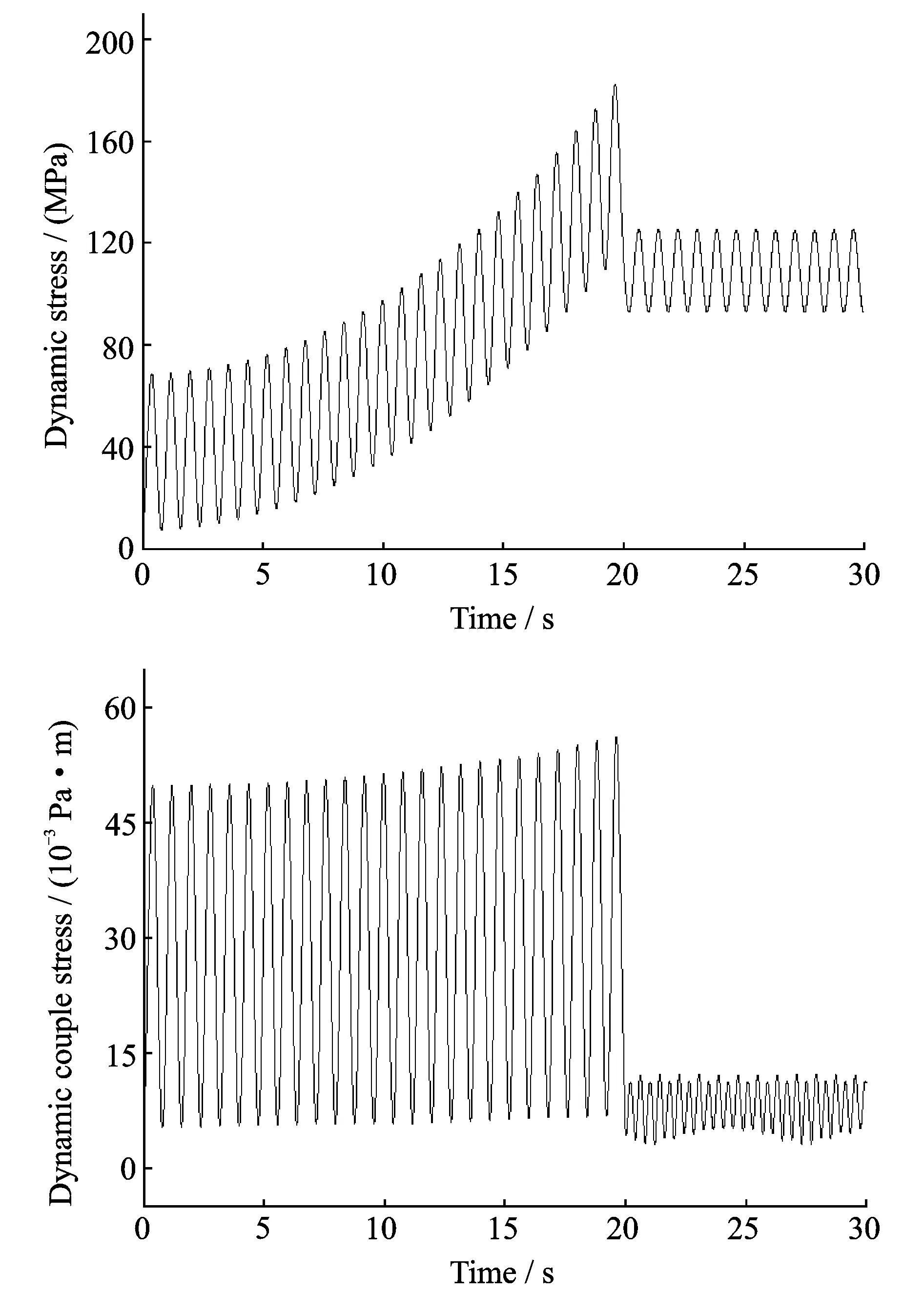
图9　旋转悬臂梁固定端处的等效应力和等效偶应力随时间变化曲线Fig.9　Equivalent stress and couple stress at the fixed end of cantilever beam versus time in the floating frame

4　结　论

利用含偶应力弹性理论进行弹性体的变形分析，结合哈密尔顿原理推导弹性体作定轴刚体转动的耦合动力学方程。通过约束变分原理，以位移和变形转角为独立变量，构造三维弹性体的六面体8个节点48个自由度的等参元，给出含偶应力弹性体作刚体转动的耦合动力学分析的有限元方程。针对绕定轴作刚体转动的悬臂梁，数值分析了旋转悬臂梁刚体转速恒定但幅值不同时的特征频率，计算分析了旋转悬臂梁绕定轴作变角速度转动的动态位移、动态变形转角、动态应力和偶应力的动力学响应。

旋转悬臂方梁不作刚体转动时，其一阶模态为悬臂梁的横向弯曲，相应的一阶模态会出现两个特征频率值。旋转悬臂方梁作定轴刚体转动时，其特征频率会出现随刚体转速增加保持不变和下降两种变化情况。针对旋转悬臂梁作定轴旋转运动的角速度变化情况，分别计算了变角加速度和恒角加速度两种工况。当旋转悬臂梁作连续的变角加速度转动时，其动态位移、变形转角、动态应力和偶应力等动力学响应比较平滑，不会出现较大的振荡。然而，当旋转悬臂梁作恒角加速度变化时，悬臂梁角速度呈线性增大至最终恒定转速，旋转悬臂梁动力学响应会出现振幅较大的周期性振动，同时在角加速度突变为零时刻会出现跳跃。模型中考虑附加惯性力，离心力、科氏力关联于角速度以及切向惯性力关联于角加速度，这些力由于角速度和角加速度的改变而发生较大改变，从而使得旋转悬臂梁的动力学响应发生较大的振荡，同时出现跳跃。

采用偶应力理论不仅可分析宏观尺寸的旋转结构，也适合于分析微观尺寸的旋转弹性结构。根据本文结果，即使对宏观旋转梁的分析，也能够给出变形转角、曲率张量、偶应力等动态响应，对弹性结构的动态分析更为全面。本文的研究可为定轴旋转系统的结构和部件如直升机旋翼、卫星天线、离心振动台、太阳能帆板和大型涡轮机叶片等的研制、测试以及动力学分析提供基础理论和数值分析方法。

[1]Kane T R, Ryan R R, Banerjee A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control and Dynamics, 1987,10(2):139—151.

[2]Al-Qaisia AA, Al-Bedoor BO. Evaluation of different methods for the consideration of the effect of rotation on the stiffening of rotating beams[J]. Journal of Sound and Vibration, 2005,280:531—553.

[3]陈思佳,章定国,洪嘉振.大变形旋转柔性梁的一种高次刚柔耦合动力学模型[J].力学学报,2013,45(2):251—256.

Chen Sijia, Zhang Dingguo, Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation[J]. Chinese Journal of Theoretical and Applied Mechanics,2013,45(2):251—256.

[4]Cai G P, Hong J Z, Yang S X. Dynamics analysis of a flexible hub-beam system with tip mass[J]. Mechanics Research Communications, 2005,32:173—190.

[5]刘铸永,洪嘉振.柔性多体系统动力学研究现状与展望[J].计算力学学报,2008,25(4):411—416.

LIU Zhu-yong, HONG Jia-zhen. Research and prospect of flexible multi-body systems dynamics[J]. Chinese Journal of Computational Mechanics, 2008,25(4):411—416.

[6]刘锦阳,洪嘉振.大范围运动空间梁的耦合动力学模型[J].上海交通大学学报,2003,37(4):532—534.

Liu Jing-yang, Hong Jia-zhen. Coupling dynamic modeling of the spatial beam undergoing large overall motions[J]. Journal of Shanghai Jiao Tong University, 2003,37(4):532—534.

[7]Simo J C, Quoc L V. On the dynamics of flexible beams under large overall motions-the planar case: Part1[J]. Journal of Applied Mechanics, 1986,53:849—854.

[8]Simo J C, Quoc L V. On the dynamics of flexible beams under large overall motions-the planar case: Part 2[J]. Journal of Applied Mechanics, 1986,53:855—863.

[9]Sugiyamaa H, Gerstmayrb J, Shabana A A. Deformation modes in the finite element absolute nodal coordinate formulation[J]. Journal of Sound and Vibration, 2006,298:1129—1149.

[10]Shabana AA, Hussien HA, Escalona JL. Application of the absolute nodal coordinate formulation to large rotation and large deformation problems[J]. ASME Journal of Mechanical Design, 1998,120:188—195.

[11]Sanborn G G, Shabana A A. A rational finite element method based on the absolute nodal coordinate formulation[J]. Nonlinear Dynamics, 2009,58:565—572.

[12]Liu J Y, Hong J Z. Geometric stiffening effect on rigid-flexible coupling dynamic of an elastic beam[J]. Journal of Sound and Vibration,2004,278:1147—1162.

[13]Liu Z Y, Hong J Z, Liu J Y. Complete geometric nonlinear formulation for rigid-flexible coupling dynamics[J]. Journal of Central South University of Technology, 2009,16:119—124.

[14]和兴锁,邓峰岩,吴根勇，等.对于具有大范围运动和非线性变形的柔性梁的有限元动力学建模[J].物理学报,2010,59(1):25—29.

He Xing-Suo, Deng Feng-Yan, Wu Gen-Yong. Dynamic modeling of a flexible beam with large overall motion and nonlinear deformation using the finite element method[J]. Acta Phys. Sinica., 2010,59(1):25—29.

[15]吴胜宝,章定国.大范围运动刚体—柔性梁刚柔耦合动力学分析[J].振动工程学报,2011,24(1):1—7.

Wu Shengbao, Zhang Dingguo. Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion[J]. Journal of Vibration Engineering, 2011,24(1):1—7.

[16]方建士,章定国.旋转悬臂梁的刚柔耦合动力学建模与频率分析[J].计算力学学报,2012,29(3):333—339.

Fang Jianshi, Zhang Dingguo. Rigid-flexible coupling dynamic modeling and frequency analysis of a rotating cantilever beam[J]. Chinese Journal of Computational Mechanics, 2012,29(3):333—339.

[17]Mindlin R D, Tiersten H F. Effects of couple-stresses in linear elasticity[J]. Archive for Rational Mechanics and Analysis, 1963,11(1):415—418.

[18]Fleck N A, Muller G M, Ashby M F, et al. Strain gradient plasticity: theory and experiments[J]. Acta Metallurgica et Materialia, 1994,42:475—487.

[19]陈少华,王自强.应变梯度理论进展[J].力学进展,2003,33(2):207—216.

Chen Shaohua, Wang Ziqiang. Advances in strain gradient theory[J]. Advanced in Mechanics, 2003,33(2):207—216.

[20]Lam D C, Yang F, Chong A C. Experiments and theory in strain gradient elasticity[J]. J. Mech. Phys. Solids, 2003,51:1477—1508.

[21]唐洪祥,管毓辉.孔口应力集中问题的Cosserat连续体有限元分析[J].东南大学学报(自然科学版),2013,43(4): 849—855.

Tang Hongxiang, Guan Yuhui. Finite element analysis of Cosserat continuum for stress concentration of holes[J]. Journal of Southeast University (Natural Science Edition), 2013,43(4):849—855.

[22]张敦福,李术才.偶应力对裂纹扩展的影响及尺度效应[J].岩石力学与工程学报,2009,28(12):2453—2458.

Zhang Dunfu, Li Shucai. Influence of couple stresses on crack growth and its scale effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(12):2453—2458.

[23]李安庆,周慎杰.双层微梁固有特性的尺寸效应[J].工程力学学报，2014,31(7):223—228.

Li Anqing, Zhou Shenjie. The size-dependent inherent property of bilayered micro-beams[J]. Engineering Mechanics, 2014,31(7):223—228.

[24]徐芝纶．弹性力学[M]．北京：高等教育出版社，2006.

Xu Zhilun. Elasticity[M]. Beijing: Higher Education Press, 2006.

[25]颜世军,刘占芳.修正的偶应力线弹性理论及广义线弹性体的有限元方法[J].固体力学学,2012,33(2):279—287.

Yan Shijun, Liu Zhanfang. A modified couple stress linear elasticity and finite element method For generalized elastic bodies[J]. Chinese Journal of Solid Mechanics, 2012,33(2):279—287.

[26]LIU Zhan-fang, YAN Shi-jun. Dynamic analysis on generalized linear elastic body subjected to large scale rigid rotations[J]. Appl.Math.Mech,2013,34(8):1001—1006.

[27]Palais B, Palais R. Euler′s fixed point theorem: the axis of a rotation[J]. J. Fixed Point Theory and Applications, 2007,2(2):215—220.

Dynamic modeling and numerical analysis of elastic body with couple stress under fixed-axis rotation with variable rotational speed

GUOXiao-wei1，LIUZhan-fang1,2，HAOZhi-ming3

(1.State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400030, China;2.College of Aerospace Engineering, Chongqing University, Chongqing 400030, China;3.Institute of Structural Mechanics, China Academy of Engineering Physics, Mianyang 621900, China)

A generalized linear elastic model is proposed with the couple-stress elastic theory. The strain and curvature tensor of the elastic body is described in kinematics by translational and rotational deformations, corresponding to the internal force stress and couple-stress respectively. For the case of the rigid body rotation with known rotational speed, the kinematics-deformation coupling kinetic model of the couple-stress elastic body is derived by using Hamilton′s principle. Moreover, the relative inertia force, centrifugal force, Coriolis inertia force and tangential inertia force are taken into account in this model. The finite element equations of the couple-stress elastic body is established using the constrained variation principle by using the hexahedron solid isoparametric element with 8 nodes and 48 degrees-of-freedom and taking the displacement and the deformation angle as independent variables. A cantilever beam rotating about a fixed axis is used here as an application example to explore the dynamic characteristics and the dynamic response. The first mode characteristic of the rotational rectangular beam goes to two cases with different constant rigid rotational velocities, one of which decreases to vanish and the other remains the same with the rotational speed increasing. The displacement, deformation rotor angle, and the dynamic stress and couple stress of the rotational beam versus time are numerically implemented while the rigid body rotates with variable speed. The dynamics analysis research for the fixed-axis rotation structure can provide theoretical model and numerical analysis method.

couple-stress elastic theory; rigid-flexible coupling; kinematics-deformation coupling model; effect of inertia force; constrained variation principle

2015-05-27；

2015-11-04

国家自然科学基金面上项目资助(11372365);国家自然科学基金委员会和中国工程物理研究院联合基金资助项目(11176035)

O326； O313．3

A

1004-4523(2016)01-0050-11

10.16385/j.cnki.issn.1004-4523.2016.01.008

郭小炜(1985—)，男，博士研究生。电话: 13648319976； E-mail: guoxiaowei1478@sina.com

刘占芳(1963—)，男，教授，博导。 电话: 13648354436； E-mail: zhanfang@cqu.edu.cn