用Padé多项式拟合法辨识动力学系统的物理参数*

杨智春， 丁允停， 王　乐

(西北工业大学结构动力学与控制研究所， 陕西 西安 710072)



用Padé多项式拟合法辨识动力学系统的物理参数*

杨智春， 丁允停， 王乐

(西北工业大学结构动力学与控制研究所， 陕西 西安 710072)

提出了一种动力学系统的物理参数辨识方法。应用Padé多项式对动力学系统的动刚度曲线进行拟合，通过最小二乘法确定Padé多项式中的系数矩阵，利用遗传算法对Padé拟合式中的参数进行优化，从而得到系统的质量矩阵、阻尼矩阵和刚度矩阵。数值算例表明该方法具有较高的辨识精度且适用于黏性阻尼系统和非黏性阻尼系统。

参数识别； 系统辨识； 结构动力学系统； Padé拟合； 最小二乘法

引　言

在动力学响应分析过程中，系统辨识起着十分重要的作用，结构动力学系统的物理参数辨识一直是结构动力学领域的研究热点。准确辨识结构的质量矩阵、阻尼矩阵和刚度矩阵，是准确地预计结构动力学响应的前提。

Phan[1]等利用系统的输入输出信号，通过状态空间模型辨识系统的质量矩阵、阻尼矩阵和刚度矩阵。Chen和Tsuei[2]同时考虑了黏性阻尼和结构阻尼来对系统的物理参数进行了辨识。Lee和Kim[3]对Chen和Tsuei的方法进行了改进，将原来方法拓展到多输入多输出系统，并在实验验证中发现，Tsuei等人的方法若从动刚度的角度出发，辨识过程将得到很大简化，且辨识结果受测量误差和噪声的影响较小。但是，正如Lee和Kim[3]在文中所说，利用结构动刚度进行动力学参数辨识的研究还很少。

广泛应用于系统降阶及参数拟合的Padé多项式是一种曲线拟合方法。Chazot[4]等将Padé多项式用于黏弹性结构降阶，其计算效率与直接计算方法相比，得到很大提高。王学雷[5]提出了一种基于Padé近似的频域辨识方法，研究了基于积分最小二乘指标的SISO时滞系统频域辨识问题。叶华[6]等利用Padé多项式来逼近时滞环节，提出了一种时滞电力系统特征值的计算方法。Fournodavlos和Nestoridis[7]从数学角度也研究了Padé在参数拟合方面的应用。作者[8]在之前的研究中，曾研究过利用Padé多项式对频域广义气动力拟合，得到时域气动力表达式，进而研究带迟滞非线性环节二元机翼的气动弹性响应问题。

本文从线性结构动力学系统的动刚度出发，采用Padé多项式拟合，对动力学系统的物理参数进行辨识。首先分别从黏性阻尼和非黏性阻尼两种动力学系统介绍了系统参数辨识方法，并通过数值仿真算例对两种动力学系统的物理参数进行辨识，验证了该方法具有较高的辨识精度。

1　系统物理参数辨识方法

1.1黏性阻尼系统

黏性阻尼结构的运动方程可以写为

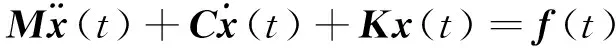
(1)

式中M，C，K分别为质量、阻尼和刚度矩阵，x(t)为位移向量，f(t)为外激励向量。

假设外激励为简谐的，即f(t)=F(ω)ejωt，则响应也是简谐的，即x(t)=X(ω)ejωt，代入式(1)，得到

(2)

式中X(ω)，F(ω)分别为x(t)，f(t)的Fourier变换。则根据系统的传递函数的定义，得

(3)

动刚度矩阵为系统传递函数矩阵的逆矩阵

(4)

Padé多项式[9]的一般形式为

(5)

式中Ai+2为修正项，βi共有l项，一般事先给出。下面将推导如何拟合出Padé多项式的系数矩阵Ai，i=0,1,2,…,l+2。

不失一般性，为简明起见，令l=2，即只考虑2个修正项Ai，即A3和A4，

将式(5)的实部和虚部分离：

简记为

(8)

式(8)为矛盾方程组，求解过程中，频率点的选取至少需要2个，其最小二乘解为

(9)

从而得到系数矩阵Ai，i=0,1,2,…,l+2。其中，(STS)-1ST为S的Moore-Penrose逆，当l>2时，修正项由更多项组成，但系数矩阵的求解过程与上述相同。

将式(5)表示为复数形式

(10)

比较式(4)，(10)，根据复数相等的充要条件并比较两式的同类项，得到：

(11)

(12)

以及

(13)

由式(11)，(13)可见，βi的取值会影响参数辨识的结果，因此，在对动刚度矩阵进行拟合时，需要对βi的取值进行优化，即βi值的确定为一个寻优过程。本文利用遗传算法对优化变量βi值的选取进行优化，优化目标为使得重构后的动刚度矩阵与原始的动刚度矩阵在关心的频率范围内其误差的范数最小，其中，重构的动刚度矩阵通过对重构的频响函数求逆获得，目标函数为

(14)

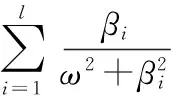
1.2非黏性阻尼系统

对非黏性阻尼结构，其阻尼项一般用核函数的卷积分表示[10]，系统的运动方程可写为

(15)

式中c(t)为核函数。

令c(t)=C0g(t)，C0为对称的正定系数矩阵，g(t)为核函数的类型。显然，当g(t)=δ(t)，δ(t)为狄拉克函数(Dirac delta function)时，式(15)退化为黏性阻尼系统。本文重点研究一种特殊的非黏性阻尼模型，其核函数为

(16)

对这种指数型阻尼模型，其核函数也称为“松弛函数”，该阻尼模型广泛用于表征黏弹性阻尼结构[11]。对式(16)进行傅里叶变换，并乘以系数矩阵C0，即可得到阻尼矩阵，显然此时阻尼矩阵为一复数矩阵，即C=CR+jCI，其中：

(17)

(18)

根据结构动力学系统的动刚度定义，由式(4)得到黏弹性阻尼系统的动刚度为

(19)

可见，黏弹性阻尼同时也具有刚度效应。将式(5)表示为

(20)

比较式(19)，(20)，由实部、虚部相等的条件以及同幂次项系数相等，得到：

(21)

(22)

(23)

(24)

2　数值仿真算例

2.1算例1

如图1所示的三自由度质量-弹簧系统，假设阻尼为黏性阻尼。

图1　带黏性阻尼的三自由度质量-弹簧系统Fig.1　3-DOF mass-spring system with viscous damping

系统的物理参数矩阵如下：

表1　系统的3阶固有频率

Tab.1　The three natural frequencies of the system

Modenumber123Naturalfrequency/Hz1.03452.96234.3948

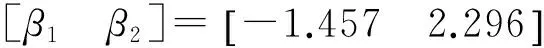
识别的频率修正项接近于零，由前文可知选用黏性阻尼模型进行辨识是合理的。由式(11)，(12)，(13)，得到：

可见，对黏性阻尼系统的物理参数矩阵进行了准确地辨识。

由式(11)，(12)，(13)，得到：

可见，当模态不完备时，本文方法对黏性阻尼系统的物理参数矩阵同样能够准确辨识。

2.2算例2

如图2所示的二自由度质量-弹簧系统，假设阻尼为黏弹性阻尼。

图2　带黏弹性阻尼的二自由度质量-弹簧系统Fig.2　2-DOF mass-spring system with viscoelastic damping

系统的物理参数矩阵为：

2.2.1用黏性阻尼模型进行辨识

此时，系统的阻尼矩阵、质量矩阵和刚度矩阵由式(11)，(12)，(13)得到：

可见，质量矩阵得到准确辨识，但识别得到的系统刚度矩阵不是常数阵，阻尼矩阵为实数矩阵，由前文所述可知，选用黏性阻尼模型对该系统进行辨识是不合理的。这里，仅给出在1～100 rad/s频率带宽范围内，辨识得到的阻尼矩阵(或刚度矩阵)与原始阻尼矩阵(或刚度矩阵)中的一些元素随频率的变化曲线对比，如图3和4所示。

图3　用黏性阻尼模型识别的阻尼矩阵Fig.3　Identified damping matrix by viscous damping model

图4　用黏性阻尼模型识别的刚度矩阵Fig.4　Identified stiffness matrix by viscous damping model

由图3和4可见，虽然刚度矩阵中的元素K11和K22的最大相对误差分别为1.99%和3.32%，但已表现出随频率变化的特性，而且阻尼矩阵的虚部信息明显缺失，所以用于辨识的阻尼模型选用黏性阻尼模型是不合理的，应按非黏性阻尼模型进行辨识。

2.2.2用非黏性阻尼模型进行辨识

当辨识阻尼模型选用非黏性阻尼模型时，采用前述针对非黏性阻尼系统的Padé多项式拟合法，对系统的物理参数矩阵进行辨识，取修正项数l=2。如图5所示为对βi的取值优化前，取不同βi值得到的辨识结果，其中实线表示的是松弛因子μ取100时的原始阻尼矩阵中的元素随频率的变化曲线。显然，需要按前一节所述对βi的取值进行优化。

由式(21)，(24)可得：

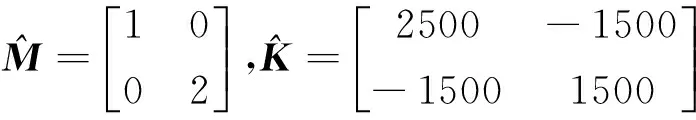
可见，质量矩阵和刚度矩阵得到准确辨识。根据式(22)，(23)并与式(17)，(18)比较，得到阻尼矩阵为：

可见，松弛因子和系数矩阵得到了精确地辨识。在1～100 rad/s频率带宽范围内，如图6所示为辨识得到的阻尼矩阵与原始阻尼矩阵的各个元素随频率的变化曲线对比(根据阻尼矩阵对称性，C21=C12，C22=C11)。显然，阻尼矩阵的辨识精度也相当高。

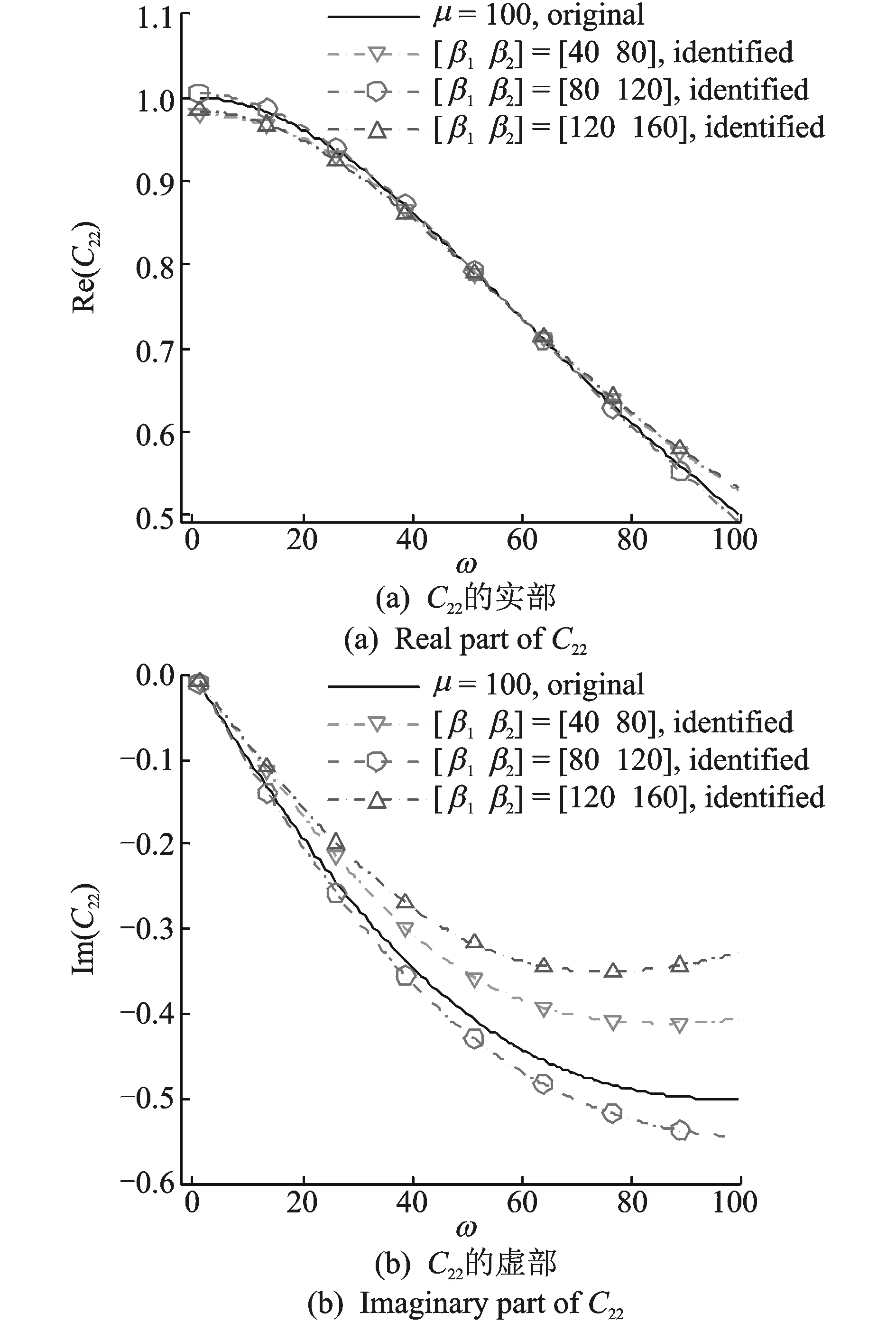
图5　不同βi取值下识别的C22的实部与虚部Fig.5　Real and imaginary part of identified C22 with different values of βi

由式(21)，(24)可得：

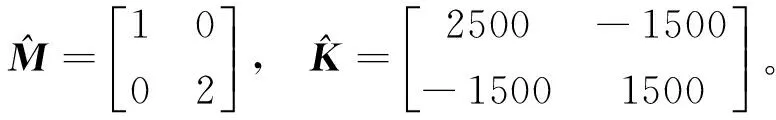
可见，质量矩阵和刚度矩阵得到准确辨识。根据式(22)，(23)并与式(17)，(18)比较，得到阻尼矩阵为：

(26a)

(26b)

可见，当模态不完备时，本文方法对非黏性阻尼系统的物理参数矩阵同样能够准确辨识。

图6　用非黏性阻尼模型识别的阻尼矩阵Fig.6　Identified damping matrix by non-viscous damping model

3　结　论

(1) 本文利用Padé多项式对系统的动刚度进行拟合，提出了动力学系统参数辨识的一种新方法，该方法同时适用于黏性阻尼系统和非黏性阻尼系统。并且，本文方法的辨识结果能够反映一定的阻尼机理，当频率修正项较小或接近为零时，用于辨识的阻尼模型应按黏性阻尼模型进行辨识；当频率修正项较大时，用于辨识的阻尼模型应按非黏性阻尼模型进行辨识。

(2) 本文以Padé多项式修正项中的参数为变量，求得辨识得到的动刚度矩阵与原始的动刚度矩阵之间的误差矩阵，以误差矩阵的范数为目标函数，通过遗传算法对修正项中的参数进行优化，从而提高Padé多项式曲线拟合的精度，辨识得到的质量矩阵、阻尼矩阵和刚度矩阵具有较高的准确度。

[1]Phan M Q, Longman R W. Extracting mass, stiffness, and damping matrices from identified state-space models[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, 2004, Providence, Rhode Island.

[2]Chen S Y, Ju M S, Tsuei Y G. Estimation of mass, stiffness and damping matrices from frequency response functions[J]. American Society of Mechanical Engineers Journal of Vibration and Acoustics, 1996, 118:78—82.

[3]Lee J H, Kim J. Development and validation of a new experimental method to identify damping matrices of a dynamic system[J]. Journal of Sound and Vibration, 2001, 246(3):505—524.

[4]Chazot J D, Nennig B, Chettah A. Harmonic response computation of viscoelastic multilayered structures using a ZPST shell element[J]. Computers and Structures, 2011, 89:2522—2530.

[5]王学雷, 邵惠鹤. 一种基于Padé近似的频域辨识与频域模型降阶新方法[J]. 控制理论与应用, 2003, 20(1): 54—58.

Wang Xuelei, Shao Huihe. New method of frequency-domain identification and model reduction based on Pagé approximation[J]. Control theory and Applications, 2003,20(1):54—58.

[6]叶华, 霍健, 刘玉田. 基于Padé近似的时滞电力系统特征值计算方法[J]. 电力系统自动化, 2013, 37(7): 25—30.

Ye Hua, Huo Jian, Liu Yutian. A method for computing eigenvalue of time-delayed power system based on Pagé approximation[J]. Automation of Electric Power Systems, 2013,37(7):25—30.

[7]Fournodavlos G, Nestoridis V. Generic approximation of functions by their Padé approximants[J]. Journal of Mathematical Analysis and Applications,2013, 408:744—750.

[8]谷迎松，杨智春. 带迟滞非线性环节二元机翼的气动弹性响应分析[J]. 机械科学与技术, 2006, 25(8): 901—904.

Gu Yingsong, Yang Zhichun. Aeroelastic response analysis of an airfoil with hysteresis nonlinearity[J]. Mechanical Science and Technology, 2006,25(8):900—904.

[9]Padé H. Sur la représentation approachée d'une fonction par des fractions rationnelles[J]. Annales de l'Ecole Normale Sup, 1892, 9 (3): 3—93.

[10]Woodhouse J. Linear damping models for structural vibration[J]. Journal of Sound and Vibration, 1998, 215(3): 547—569.

[11]Biot M A. Variational principles in irreversible thermodynamics with application to viscoelasticity[J], Physical Review, 1955, 97(6):1463—1469.

Identifying physical parameters of structural dynamical system using Padé approximation

YANGZhi-chun,DINGYun-ting,WANGLe

(Institute of Structural Dynamics and Control, Northwestern Polytechnical University, Xi′an 710072, China)

A new identification method for the physical parameters of structural dynamical system is proposed. The Padé approximants is used to fit the dynamic stiffness curve of the structural dynamical system, and the coefficient matrices in the Padé polynomial are determined by the least squares method.In addition, genetic algorithms is adopted to optimize the parameters in Padé polynomial. Then the mass, damping and stiffness matrices in the physical space can be extracted from the Padé polynomial. Numerical examples illustrate that the proposed method has good accuracy and is effective for viscous or non-viscous damped systems.

parameters identification; system identification; structural dynamical system; Padé approximants; least squares method

2014-07-17；

2015-06-26

高等学校学科创新引智计划资助项目(B07050)；国家自然科学基金资助项目(11402205)

V214.1

A

1004-4523(2016)01-0024-07

10.16385/j.cnki.issn.1004-4523.2016.01.004

杨智春(1964—)，男，教授，博士生导师。电话：(029)88460461；E-mail:yangzc@nwpu.edu.cn