太赫兹光子晶体光纤单模传输特性的研究

胡守重，刘泽男

（兰州理工大学理学院，甘肃 兰州730050）

太赫兹光子晶体光纤单模传输特性的研究

胡守重，刘泽男

（兰州理工大学理学院，甘肃 兰州730050）

利用全矢量有限元法并结合损耗理论对全内反射型太赫兹光子晶体光纤的单模传输带宽进行了深入的研究。结果表明，光纤的限制损耗以及单模传输带宽可以通过改变光子晶体光纤的占空比、空气孔间距、空气孔层数等结构参数进行灵活的调节，并与其他文献利用归一化频率法得到的结果相吻合。

太赫兹波；光子晶体光纤；单模传输；限制损耗

1　概述

太赫兹波［1-2］（Terahertz，简称THz），是指频率在0.1～10THz（1THz＝1012Hz），对应的波长为3000～30μm范围内的电磁波。由于太赫兹波对空气中水蒸气的吸收非常强，使其具有很大的自由空间损耗，并且传输方向难以控制，因此太赫兹波导就成为研究太赫兹传输的重要基础。

光子晶体光纤［3-4］（PCF），又被称为微结构光纤，它是一种带有线缺陷的二维光子晶体。光子晶体光纤相比普通光纤来说，具有结构设计的灵活性以及优异的传输性能。因此，光子晶体光纤被广泛研究和应用。

利用全矢量有限元法［5］并结合损耗理论对全内反射型太赫兹光子晶体光纤（THz-PCF）的传输特性进行了深入的研究，分析了占空比、空气孔间距、空气孔层数对其传输特性的影响。

2　光纤结构和理论基础

THz-PCF的横截面如图1所示。其中Λ为孔间距，d为空气孔直径，空气孔层数为四层，灰色基底填充的是环烯烃共聚物（COC），在THz波段的折射率为n1=1.5258，空气的折射率n0=1。

图1　太赫兹光子晶体光纤的截面示意图

由麦克斯韦方程组可以得到电场E的矢量波动方程

式中β是传播常数。将方程（2）代入（1）并进行区域离散化可以得到本征值方程

3　光纤的特性分析

3.1限制损耗及单模传输特性

在PCF中，光在其纤芯中传输时会通过空气孔的间隙泄露到包层，从而造成光纤传输能量的损耗，称之为限制损耗［6］。基模的限制损耗Lcon可通过下式计算其中Im（neff）表示基模模式有效折射率的虚部，根据PCF的模式选择理论［7-8］，基模损耗小于0.1dB/m，高阶模损耗大于1dB/m时该PCF可实现单模传输。为简化分析，选取高阶模中限制损耗最低的模式作为研究对象，通过大量的仿真模拟发现二阶模LP01的限制损耗总是除基膜之外最小的，因此我们选取限制损耗最小的二阶模作为参考对象。

图2　∧=500μm时基模与二阶模限制损耗随d/∧的变化曲线

图3　d/∧=500μm时基模与二阶模限制损耗随dα∧的变化曲线

图4=500μm，d/=0.5时基模与二级模限制损耗随包层空气孔层数的变化曲线

图5　孔间距=500μm，占空比d/=0.5，空气孔层数为4层时基模与二级模限制损耗的变化曲线

图6　孔间距=500μm，占空比d/=0.5，空气孔层数为4层时时归一化频率的变化曲线

3.2模式有效折射率

各阶模式的有效折射率值只有满足在纤芯和包层折射率之间才能被激发在纤芯传输，因此研究基模的模式有效折射率具有非常重要的意义。而且有基模的模式有效折射率值可以计算出光纤波导色散随频率的变化曲线。该PCF不同结构参数下的模式有效折射率值如图7所示。

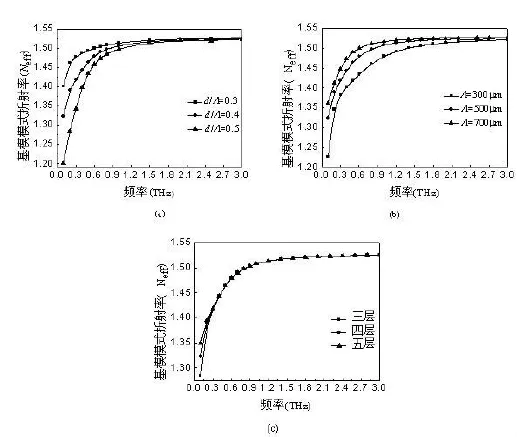
图7　模式有效折射率随孔间距、占空比、空气孔层数的变化曲线

由图7可知，基模模式折射率随着频率的增加而增加，且趋于一定值。孔间距一定时，d/越大，基模折射率越小；当占空比d/一定时，越小，模式折射率越小。同时随着层数的增加，基模模式折射率有所增加。

4　结论

本文利用有限元分析法并结合损耗理论对全内反射型太赫兹光子晶体光纤的单模传输范围进行了深入的研究，分析了占空比、空气孔间距、空气孔层数对该光子晶体光纤传输特性的影响。结果表明，单模传输范围随占空比、孔间距、空气孔层数的减小而增大；限制损耗随占空比、空气孔间距、空气孔层数的增大而减小；模式有效折射率随占空比的增大而减小，随孔间距、空气孔层数的增大而增大。

［1］ 姚建铨，迟楠，杨鹏飞，等.太赫兹通信技术的研究与展望［J］.中国激光，2009，36（9）：2213.

［2］ 刘长蕊，许新统，张莹莹，等.低损耗Topas环烯烃共聚物光纤研究［J］.深圳大学学报：理工版，2014，31（2）：164-168.

［3］ BirksT A，KnightJ C，RussellPSJ.Endlesslysingle-mode photoniccrystalfiber［J］.Opticsletters，1997，22（13）：961-963.

［4］ Cerqueira Jr S A.Recent progress and novel applications of photonic crystal fibers［J］.Reports on progress in physics，2010，73（2）：024401.

［5］ Dhatt G，Lefran？ois E，Touzot G.Finite element method［M］. JohnWiley&Sons，2012.

［6］ 王豆豆，王丽莉.新型光学聚合物——Topas环烯烃共聚物微结构光纤的设计及特性分析［J］.物理学报，2010（5）：3255-3259.

［7］ Wong W S，PengX，McLaughlinJ M，etal.Breaking the limit of maximum effective area for robust single-mode propagation in optical fibers［J］.Optics letters，2005，30（21）：2855-2857.

［8］ 陈艳，周桂耀，夏长明，等.具有双模特性的大模场面积微结构光纤的设计［J］.物理学报，2014，63（1）：14701-014701.

［9］Mortensen N A.Effective area of photonic crystal fibers［J］. Optics Express，2002，10（7）：341-348.

TN292.11