基于格子玻尔兹曼方法的可激发系统物理性质研究

陈　超，邓敏艺，孔令江

(1.桂林航天工业学院 理学部，广西 桂林 541004；2.广西师范大学 物理科学与技术学院，广西 桂林 541004)



基于格子玻尔兹曼方法的可激发系统物理性质研究

陈超1，邓敏艺2，孔令江2

(1.桂林航天工业学院 理学部，广西 桂林 541004；2.广西师范大学 物理科学与技术学院，广西 桂林 541004)

基于格子玻尔兹曼方法的D2Q9模型，研究可激发系统的能量和熵.数值计算结果表明：相同系统参数下，不同稳定波态系统的平均能量值接近，但熵值不同；在螺旋波失稳进入混沌态过程中，系统内能急剧减少，熵值增加；系统能量不足是螺旋波失稳的主要原因.

可激发系统；螺旋波；内能；熵

医学研究表明，心脏是一个开放系统，人体的心肌组织属于可激发系统.在正常情况下，人体心脏的心肌电信号是以靶波形式存在，引发生命危险的心脏纤维性颤动与心肌电信号出现螺旋波失稳有关[1-5].科研工作者已对激发介质中螺旋波的失稳机制和驱逐螺旋波的方法进行了研究[6-10].可激发系统相关物理量变化规律的研究对防治心脏病有重要意义.格子玻尔兹曼方法是一种介观层次的数值模拟方法[11]，具有程序代码简单、并行运算速度快、计算结果精度高等优点，可模拟复杂系统各种演化行为，近年来在各个领域得到了广泛应用.笔者拟以Selkov反应扩散系统作为媒介，基于格子玻尔兹曼方法的D2Q9模型，研究可激发系统的能量和熵.

1　Selkov反应扩散系统和D2Q9模型

1.1Selkov反应扩散系统

描述Selkov反应扩散系统[12]的动力学方程为

(1)

(2)

其中：浓度ρ1为慢变量，浓度ρ2为快变量，相应的粒子分别称为第1种粒子和第2种粒子；α，β，χ，κ为系统参数；D1，D2分别为第1种粒子和第2种粒子的扩散系数.系统参数取适当值时，Selkov反应扩散系统为一个可激发系统[13].

1.2格子玻尔兹曼方法的D2Q9模型

格子玻尔兹曼方法的D2Q9模型[14]如图1所示.图1中，ei为i方向的单位速度.

图1　D2Q9模型Fig.1　Model D2Q9

平衡态分布函数取如下最简单的形式

(3)

其中：ωi为权系数，在不同方向对应的值分别为

考虑粒子间发生化学反应,需要在概率密度函数fi(r,ei,t)的输运方程中加入反应项，那么描述系统演化的方程变为如下形式

(4)

其中：fi(r,ei,t)表示粒子t时刻在格点r处具有速度ei的几率；τ为弛豫时间.采用多尺度方法与泰勒展开等数学手段处理后，可由(4)式导出(1)，(2)式.

系统参数值为：a=0.76, b=0.02, χ=0.1, κ=5.0, D1=D2=0.1；系统大小为300×300个格子；初态ρ1=7.451 46, ρ2=0.025 61. 在无滑反弹边界条件下，通过不同的扰动方式，系统可以演化出如图2所示的4种斑图.若在系统的左边长为300个格子、宽为1个格子的区域施加大小为ρ1=6.5, ρ2=0.8 的周期性扰动，系统可形成行波，如图2a所示；若在系统中心区域施加大小为ρ1=6.5, ρ2=0.8的周期性扰动，系统可形成环状的靶波，如图2b所示；若将传导到系统中央的行波截断，行波将会在截断处发生卷曲而逐渐发展成螺旋波，如图2c所示；保持其他参数不变，当a=0.774 6时，系统从螺旋波态开始演化，最后进入到时空混沌态，如图2d所示.

图2　系统演化出的4种斑图Fig.2　Four types of patterns that appear in the course of system evolution

2　系统的能量和熵

2.1系统的能量

系统演化形成的各种斑图属于耗散结构，耗散结构的建立和稳定与系统的能量有关.结合格子玻尔兹曼方法对内能的定义，且只考虑粒子间的动能，系统能量表达式为

(5)

通过数值计算得到系统4种情况下能量与时间的关系曲线(见图3).图3a,b,c表明：系统分别处在行波、靶波和螺旋波3种稳定波态时，系统能量都随时间作周期性变化，但是不同波态的系统能量波动的幅度不同；在相同系统参数下，行波态时系统平均能量为3.664 03 J，靶波态时系统平均能量为3.661 3 J，螺旋波态时系统平均能量为3.514 62 J，3种状态的系统平均能量相差不大，说明系统能量主要由系统参数决定，与初始条件关系不大；保持其他参数不变，当a=0.774 6时,系统螺旋波经长时间演化，最后进入时空混沌态.从图3d可知，螺旋波失稳过程中，系统能量急剧降低，能量远小于螺旋波态时的能量.耗散结构理论认为螺旋波态失稳源于系统提供的能量过小，当系统能量小于维持螺旋波斑图所需的最小能量时，系统的螺旋波斑图将变得不稳定，甚至演化成时空混沌斑图.

2.2系统的熵

结合玻尔兹曼H定理，考虑到格子玻尔兹曼方法中格点上质量和速度需满足守恒方程，构建离散格式的熵函数[15]如下

(6)

其中：h0,h1和h2是与速度分布函数有关的函数.当S最小时，系统处于平衡态.另设系统处在平衡态时各方向上的平衡态分布函数为

(7)

其中：k=1,2,…,4.

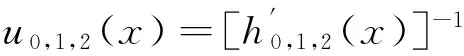
(8)

其中：k=1,2,…,4.

图3　4种情况下系统能量与时间的关系曲线Fig.3　Relation curve between system energy and time in four cases

熵函数为

(9)

在相同参数下，3种状态的系统熵与时间的关系曲线如图4所示.由图4a可以看出：螺旋波态时系统熵值最大，靶波态时次之，行波态时最小，由此得知螺旋波态时系统有序度最低，靶波态时系统有序度较高，行波态时系统有序度最高.将图3a，b，c 与 图4a对比发现：在系统参数相同情况下，系统平均能量越大，熵值反而越低，斑图越稳定，系统有序度越高.将图3d与图4b对比发现：在系统螺旋波失稳过程中，系统向能量减少、熵值增大方向变化，系统有序度降低.

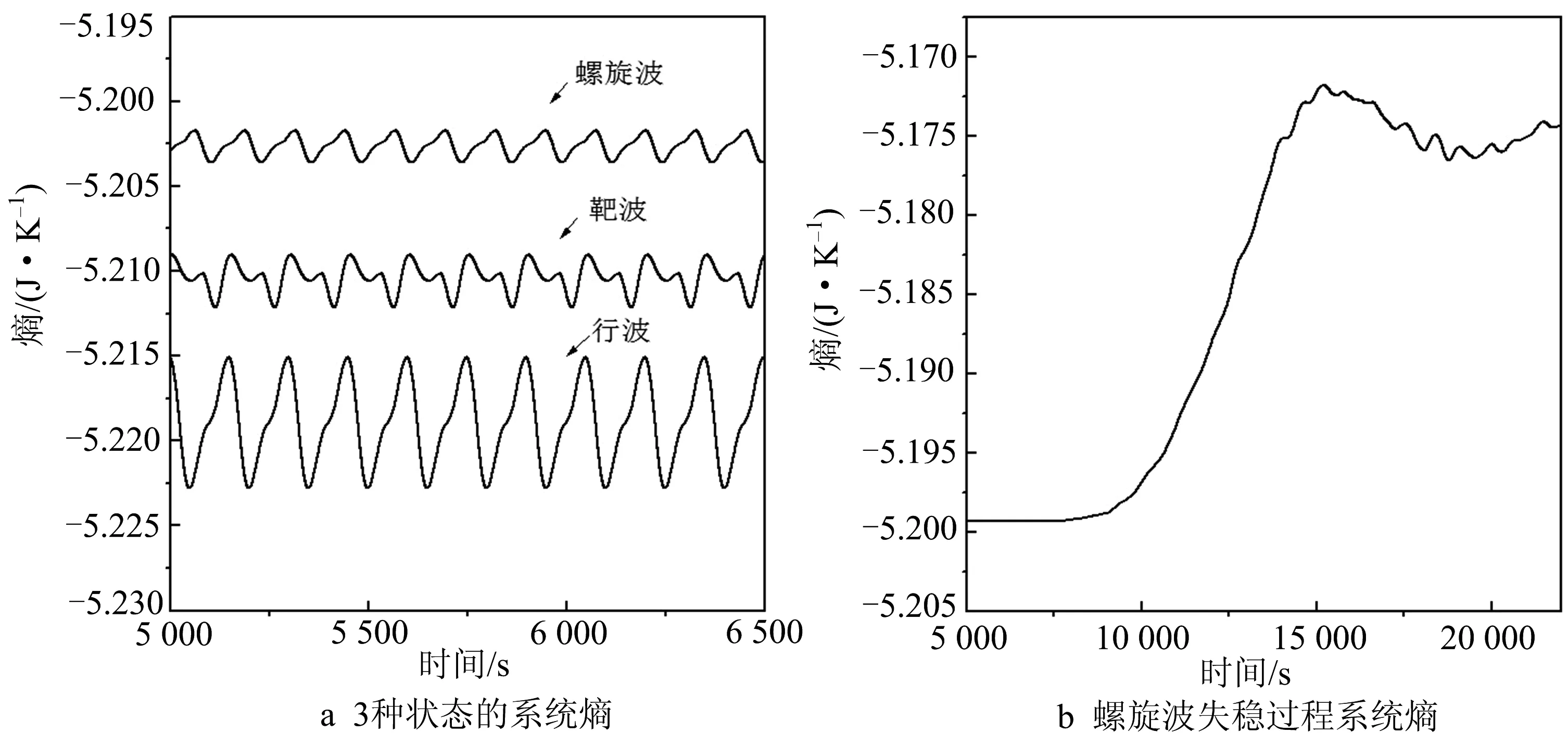
图4　系统熵与时间的关系曲线 Fig.4　Relation curve between system entropy and time

3　结束语

基于格子玻尔兹曼D2Q9模型对Selkov反应系统的能量和熵的研究表明：在相同系统参数下，处于各种稳定波态的系统能量是周期性变化的，且系统平均能量差别不大，说明系统能量主要取决于系统参数，而与扰动方式关系不大；螺旋波的失稳是系统的能量不足引起的；行波的有序度最高，靶波的有序度次之，螺旋波的有序度最低；在螺旋波失稳过程中，系统向熵增大方向变化，与孤立系统热力学熵的变化相似.

[1]CHEN P S, GARFINKEL A, WEISE J N, et al. Computerized mapping of fibrillation in normal ventricular myocardium[J]. Chaos, 1998, 8 (2): 127-132.

[2]DAVIDENKO J M, PERTOSOV A V, SALOMONSZ P, et al. Stationary and drifting spiral waves of excitation in isolated cardiac muscle[J]. Nature, 1992, 355 (2): 61-65.

[3]欧阳颀. 反应扩散系统中螺旋波的失稳[J]. 物理, 2001, 30 (1): 30-35.

[4]DAI Y, WEI H M, TANG G N. The evolution of spiral waves in inhomogeneous excitable media[J]. Acta Phys Sin, 2010, 59 (9): 5979-5984.

[5]WITKOWSKI F X, LEON L J, PENKOSKE P A ,et al. Spatiotemporal evolution of ventricular fibrillation[J].Nature, 1998, 392 (3): 78-82.

[6]邓敏艺, 唐国宁, 孔令江, 等. 激发介质中螺旋波失稳的微观机理研究[J]. 物理学报, 2010, 59 (4): 2339-2344.

[7]YANG J H, XIE F G, QU Z L, et al. Mechanism for spiral wave breakup in excitable and oscillatory media[J]. Phys Rev Lett, 2003, 91 (14): 119801-119900.

[8]钟敏, 唐国宁. 用钙离子通道激动剂抑制心脏组织中的螺旋波和时空混沌[J]. 物理学报, 2010, 59 (5): 3070-3076.

[9]高加振, 谢玲玲, 谢伟苗, 等. FitzHugh-Nagumo系统中螺旋波的控制[J]. 物理学报, 2011, 60 (8): 080502.

[10]韦海明, 唐国宁. 交替行为对螺旋波影响的数值模拟研究[J]. 物理学报, 2011, 60 (4): 040504.

[11]郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009: 8-10.

[12]李如生. 非平衡热力学和耗散结构[M ]. 北京: 清华大学出版社, 1986: 161-238.

[13]邓敏艺, 施娟, 李华兵, 等. 用晶格玻尔兹曼方法研究螺旋波的产生机制和演化行为[J]. 物理学报, 2007, 56 (4): 2012-2017.

[14]郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社， 2009： 48-49.

[15]KARLIN I V, ERRANTE A F, OTTINGER H C. Perfect entropy functions of the Lattice Boltzmann method[J]. Euro Phys Lett, 1999, 47 (2): 182-188.

(责任编辑郑小虎)

Research on physical property of the excitation system based on Lattice Boltzmann method

CHEN Chao1， DENG Minyi2， KONG Lingjiang2

(1. Faculty of Science， Guilin University of Aerospace Technology， Guilin 541004， China;2. College of Physical Science and Technology， Guangxi Normal University， Guilin 541004， China)

Based on D2Q9 model of Lattice Boltzmann method, the energy and entropy in the Selkov reaction-diffusion system were studied in the paper. The numerical results showed that under the same system parameters the average energy value of the various steady wave states system was approximate, but their systemic entropy was different. In the process of the breakup of the spiral wave and evolving into the chaotic state, the energy of system decreased drastically, while the entropy increased. The lack of system energy was the primary cause of the spiral wave instability.

excitation system; spiral wave; energy; entropy

10.3969/j.issn.1000-2162.2016.05.008

2016-03-10

国家自然科学基金资助项目(11365003)

陈超(1978-)，男，广西桂林人，桂林航天工业学院讲师.

O552

A

1000-2162(2016)05-0045-05