回到概念:基于对称,理解分类
——以“圆的分类讨论问题”习题课为例
2016-09-21江苏省苏州市阳山实验初级中学校孙凯
☉江苏省苏州市阳山实验初级中学校孙凯
回到概念:基于对称,理解分类
——以“圆的分类讨论问题”习题课为例
☉江苏省苏州市阳山实验初级中学校孙凯
学生在小学阶段就学习过圆,但却是初中阶段最后研究的一种平面图形,什么原因呢?因为圆综合了七、八年级三角形、四边形中大多性质,特别是圆兼有轴对称和中心对称的性质,所以能否顺利解决圆的有关问题,往往意味着对整个平面几何都有深刻的理解和掌握.与圆有关的习题有很多都需要分类讨论,基于这样的现实,我们设计了一节“圆的分类讨论问题”习题课教学设计,供分享.
一、“圆的分类讨论问题”习题课教学设计
教学环节(一):基于轴对称的分类讨论问题
例1(原创题)如图1,直线AB经过圆心O,弦CD经过圆心O.
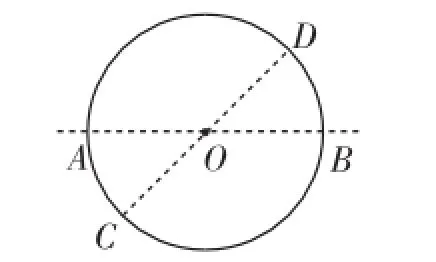
图1
(1)圆O的对称轴是________;
(2)若CD=2cm,则圆O的半径为_____;
(3)若∠AOC=60°,连接BD,请指出△BOD的形状;
(4)在图1中作出点D关于直线AB的对称点D′,求证点D′在圆O上.
教学预设:对于第一问,要注意填写直线AB或者弦CD所在直线,由于对称轴是直线,如果只写弦CD是不恰当的.第二问主要考查识别经过圆心的弦CD就是直径,从而可以直接写出1cm.第三问中△BOD是等边三角形.第四问有简单的作图方法,比如以B为圆心、BD的长为半径作弧,交圆O于点D′;证明时注意要回到圆的定义,即连接OD,设法根据对称性证出OD′=OD即可.这里也是体会点D、D′关于直径对称的基本图形,为后续问题的探究积累经验.
同类变式:(2015年浙江义乌,改编)在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心、5为半径的圆上.连接PA、PB.
(1)分析PB有没有最小值,如果有直接写出PB的最小值;
(2)小凡同学们练习(1)后发现:PB有最大值!你会分析PB的最大值吗?
(3)若PB=4,求PA的长;
(4)当∠PCB=60°时,求点P到直线AC的距离.
预设讲评:这是一道无图考题,先画出草图分析,如图2,当点P在直线AC上时,可以获得相应的PB的最小值和最大值,分别为2、8.这样也就解决了第一、二问,从图3来看,这里的P1、P2体现了关于圆心C的中心对称性质.
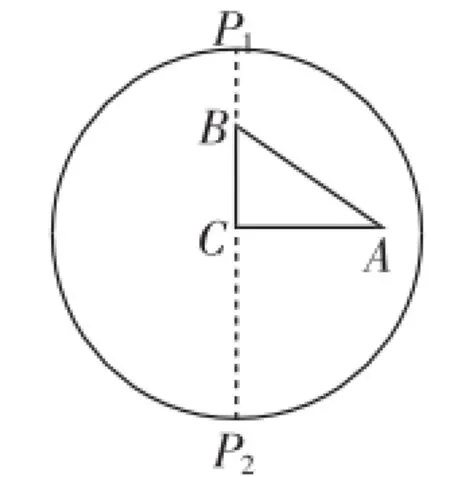
图2
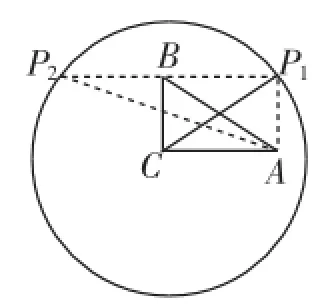
图3
对于第三问,仍然需要基于对称的启示,考虑两种可能,如图3.
在图3中,首先确认四边形AP1BC为矩形,且点P1、P2关于直线BC对称,这样就容易求出AP1=3,AP2=(在Rt△AP1P2中).
教学环节(二):弦所对圆周角的分类讨论问题
例2△ABC为⊙O的内接三角形,若∠AOC=160°,求∠ABC的度数.
教学预设:这道习题没有图,首先需要构造出可能的图形,如图4,可见∠ABC有两种可能,分别在优弧、劣弧上,故有两解:80°或100°.

图4
反思变式:这道习题有多种不同的变式可能如下所示.
同类变式1:在⊙O中,弦AC所对的圆心角∠AOC=160°,则弦AC所对的圆周角∠ABC是多少度?
同类变式2:半径为2cm的⊙O中,弦AB的长为2cm,则弦AB所对的圆周角度数是多少?
同类变式3:点O是△ABC的外心,若∠BOC=80°,求∠BAC的度数.
教学环节(三):直径与圆的位置关系的分类讨论问题
(1)求点A、B的坐标;
(2)求原点O到直线l的距离;
(3)若圆M的半径为2,圆心M在y轴上,当圆M与直线l相切时,求点M的坐标.
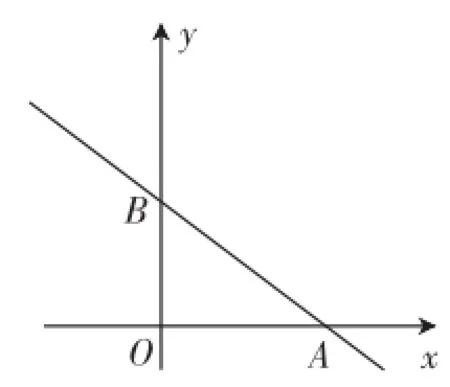
图5
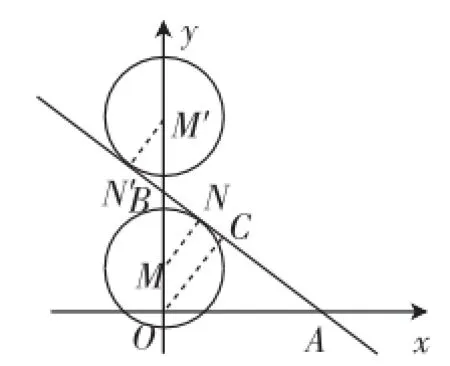
图6
教学预设:(1)求直线与x、y轴的交点时,分别令y与x为0,求出x与y的值,即可确定出A与B的坐标;(2)原点O到直线l的距离就是Rt△ABO斜边上的高,利用面积法即可求解;(3)需要考虑两种不同的相切位置,如图6,当M在B点的下方时,,即点M的坐标为;当M在B点的上方时,,即点M的坐标为
同类变式:(2015年山东烟台,18,3分)如图7,直线l∶y=-x+1与坐标轴交于A、B两点,点M(m,0)是x轴上一动点,以点M为圆心、2个单位长度为半径作⊙M,当⊙M与直线l相切时,求m的值.
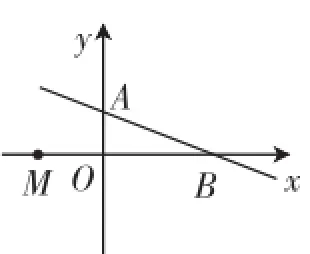
图7
教学环节(四):课堂小结与当堂检测
小结问题1:通过这节课,你觉得圆中有些问题需要分类讨论?
小结问题2:对于无图的图形问题,你觉得要注意些什么?除了在圆中无图题前容易出现分类讨论现象,在三角形或四边形的学习中,你是否也积累过类似的经验呢?举例说说.
当堂检测:(原创题)如图8,圆O中,直径AB、CD所成的锐角为40°.
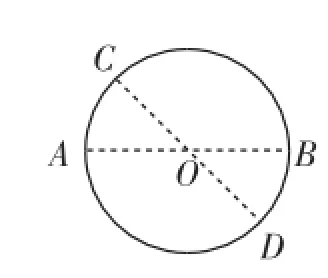
图8
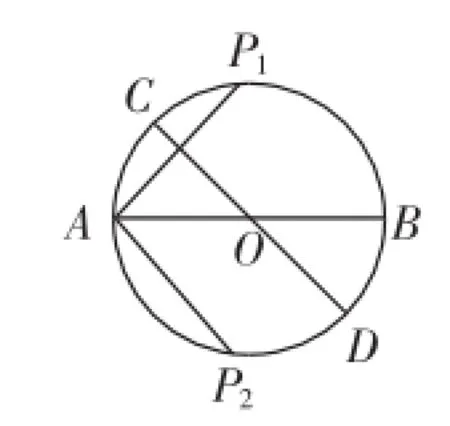
图9
(1)过点C作AB的垂线交圆O于点E,请指出弦CE与AB的位置关系;
(2)在(1)的条件下,连接OE,求∠DOE的度数;
(3)连接BD,求∠ABD的度数;
(4)若圆中有一点P,连接AP、AC,当∠BAP=50°时,求∠CAP的度数.
设计意图:第一问主要复习垂径定理的基本图形;第二问主要是根据对称性质,发现∠AOE=∠AOC=∠BOD=40°,于是∠DOE=100°;第三问在等腰△BOD中思考,顶角∠BOD=40°,于是∠ABD=70°;第四问需要分类讨论,如图9,基于对称的启示,有点P1、点P2两种可能,特别是及时发现AP1⊥CD,这时再分析出∠CAP的两种可能的答案分别为20°、120°.
二、教学立意的跟进阐释
1.预设问题驱动,引导学生“回到概念去解题”
从上面的课例来看,我们预设了大量的习题,特别是原创题及后续的系列问题,意图通过这些问题驱动,引导学生“回到概念去解题”,即基于对称性质思考分类讨论,或者基于弦所对的圆周角有两种可能(在优弧、劣弧上),或者直线与圆相切时要考虑不同的位置关系等,让学生理解这些分类讨论的合理与自然,而不是人为制造麻烦.
2.预设追问讲评,促进思维向“四面八方打开”
事实上,除了圆具有多种对称性质,之前所学的平行四边形也是中心对称图形,特殊的平行四边形,如矩形、菱形还同时兼具轴对称性质,这些对称性质往往也会决定平行四边形的相关考题可能有多解出现,如果能引导学生从对称的高度认识和反思这些分类讨论问题的结构,那么将会对数学问题有深刻的理解和洞察,包括对数学的和谐性、一致性的认识也会达到一定的高度.当然,这也是我们在“课堂小结问题2”中安排学生“举例说说”的教学立意.
1.鲍建生,顾泠沅,等.变式教学研究[J].数学教学,2003(1,2,3).
2.章建跃.全面深化数学课改的几个关键[J].课程·教材·教法,2015,35(5).Z
