一道高考模拟错题的分析与启示
2016-11-21首都师范大学附属云岗中学冯会哲郭文华
☉首都师范大学附属云岗中学 冯会哲 郭文华
一道高考模拟错题的分析与启示
☉首都师范大学附属云岗中学冯会哲郭文华
在高三下学期,笔者选用了北京市东城区2015年高三三模试卷数学文科第17题作为课后作业.讲评时,发现该题第三问有两种解法,两个答案.笔者对其进行研究分析,发现该题所给条件不足,不完善,导致了结论的不唯一.本文将详加论说.
一、题目呈现
如图1,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=90°,平面ABCD⊥平面BCEG.
(1)求证:CE⊥BD;
(2)若BC=CD=CE=2AD=2BG=2,求证:AG∥平面BDE;
(3)求几何体EG-ABCD的体积.
(北京市东城区2015年高三三模试卷数学文科第17题)
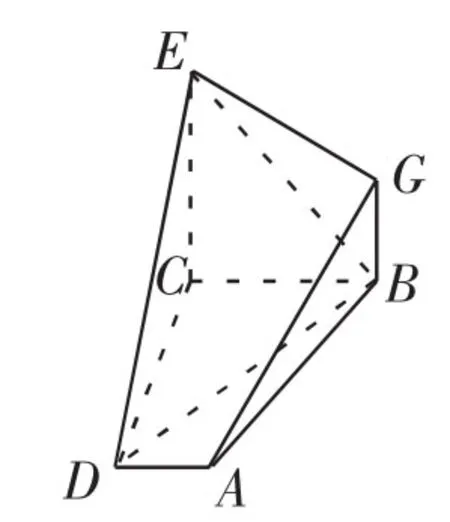
图1
二、两种解法,两个答案
此题的第三问,标准答案及部分学生解答如下:如图2,连接BG.由于CD⊥BC,平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC,所以CD⊥平面BCEG.
同理可证BG⊥平面ABCD.
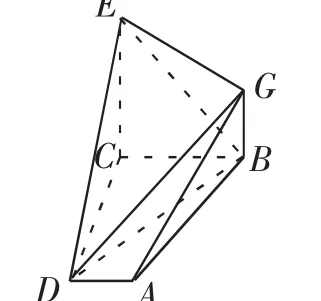
图2
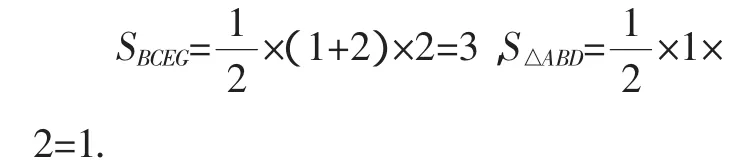
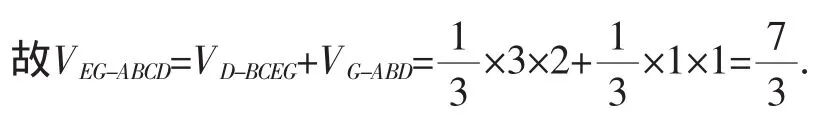
也有部分的同学解答如下:
连接AE,AC,如图3.
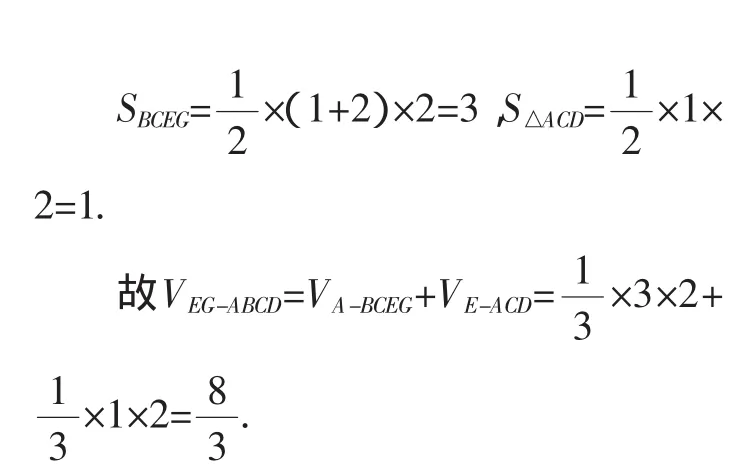
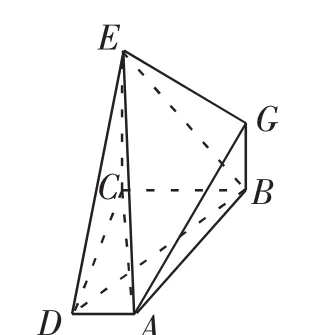
图3
学生提出疑问,这两种解法看起来都对,按道理答案应该一样,为什么会是两个答案?哪种解法出错了,错在哪?笔者仔细分析了题目,添加辅助线后两种解法都没有错,而是题目出错了.题目条件给的不严谨,导致了两种解法,两个答案.
三、错因分析及题目修正
1.从图形的角度说明
笔者引导学生,从数的运算来看,数值不同;接下来就从形入手,观察这个几何体的形状.此题所涉及的几何体为多面体,而题目条件描述的多面体并不唯一.见多面体的定义:若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面.相邻两个面的公共边叫做多面体的棱.棱与棱的公共点叫多面体的顶点[1].
此题虽然各顶点都明确了,但是由哪几个平面多边形围成的?并不明确.此题中直线AE、DG是异面直线.把它们放在棱长为2的正方体模型中,如图4所示.题目所给的相当于从正视图的方向去看,有些学生缺乏空间想象的“火眼金睛”判断不出,笔者借助几何画板,把图4顺时针旋转90°得到图5,相当于换一个视角,从左视图角度去看,学生很容易判断出AE、DG是异面直线.A、D、E、G四点不共面,G点不在面ADE上(图6);E点不在面ADG上(图7).而题目并没有给出相邻两个面的公共边,即少给一条棱.所以,涉及这四点的面可能是由面ADE和面AEG围成的(见图8),也有可能是由面DEG和面ADG围成的(见图9).
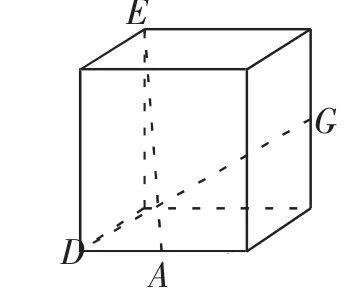
图4
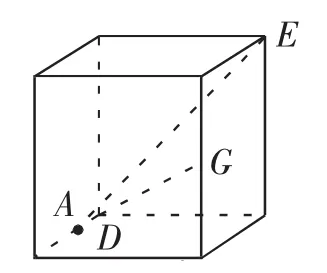
图5
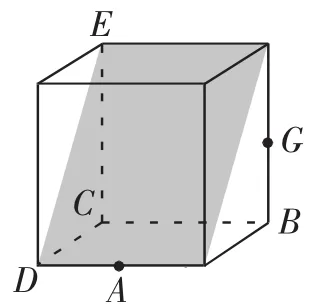
图6
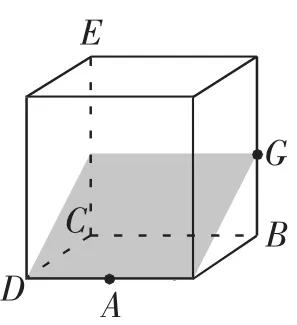
图7
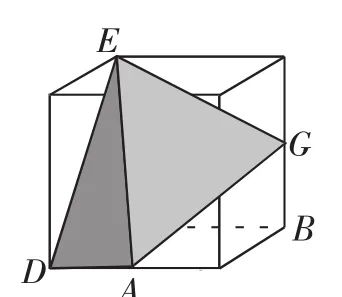
图8

图9
学生由于空间想象能力不足,误认为A、D、E、G这四个点是共面的,才会觉得两个解法应该有同一个答案.而该题所给条件能画出两个满足题意的多面体,而这两个多面体的形状是不同的,体积也是不同的.学生的两种解法实际求的是不同的几何体,所以答案是不同的.
2.从理论层面说明
教师引导学生,仅从形上观察出A、D、E、G四点不共面还不够.摆在桌子上的几何体实物,同学们可以围着它从不同角度观察;画在试卷上的几何体,同学们作答时既不方便做到换一个角度去观察它(就像图4到图5),也不能借助几何画板来画图.这就需要我们炼就“火眼金睛”,从题目给的图1上就能看出A、D、E、G四点不共面.这就需要同学们有一定的知识储备,了解相关的理论依据.
带着学生复习以下结论并给出证明.
结论:设a、b是两条异面直线,在直线a上任取两点A、B,在直线b上任取两点C、D,则直线AC、BD仍然是异面直线.
证明:假设直线AC、BD不是异面直线,则AC、BD共面,则AB、CD共面,即a、b共面,这与已知条件a、b是两条异面直线矛盾.所以,假设不成立,所以直线AC、BD是异面直线.
此题中,直线AD、EG是异面直线,显然直线EA、DG是异面直线,若同学们熟悉此结论,很容易根据题干中图1判断出A、D、E、G这四个点是不共面的,这个多面体的形状没描述清楚,体积不唯一.
3.题目的修正
题目的修正,包括两部分:图形的修正和题干部分的修正.图形部分需要再添加一条棱,AE或DG,就能确定几何体的形状,答案也就唯一了.
题干文字部分也需要改,第(2)问的条件之前有“若”字,这说明条件只适用这一问.条件“BC=CD=CE=2AD= 2BG=2”出现在题干中,第(3)问才可以用.这也是学生易错点,是该强调的地方.平时练习中,不少学生误把小前提的条件用到下一问,而惋惜失分.
所以本题题干文字部分应该改为:
如图1,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=90°,平面ABCD⊥平面BCEG.BC=CD=CE=2AD=2BG=2.
(1)求证:CE⊥BD;
(2)求证:AG∥平面BDE;
(3)求几何体EG-ABCD的体积.
或改为:如图1,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=90°,平面ABCD⊥平面BCEG.
(1)求证:CE⊥BD.
(2)若BC=CD=CE=2AD=2BG=2,
①求证:AG∥平面BDE;
②求几何体的体积.
四、几点启示
1.重视概念
学生用两种方法,得到两个答案之后,找不出问题出在哪里.笔者讲评时指出实质是学生对多面体的概念掌握得不牢.误以为多面体的顶点确定了,几何体的形状就确定了.实质上,围成多面体的平面多边形确定了,几何体的形状才能确定.最终是回归定义之后,问题才得以解决.笔者强调,高三的后期复习,学生不仅要做题,也要回归课本,熟悉基本的概念、定义.
2.强调长方体模型的重要作用
A、D、E、G这四个点是不共面的,过E作AD的平行线EF,G点不在面ADEF上.通过以下图10和图11的对比,学生很清楚地看到借助长方体模型更直观.在这个题的分析过程中,学生多次感受到以长方体模型为载体,更直观、更好理解.笔者适时强调长方体模型的工具性作用.长方体是立体几何学习中的基本几何体,其中蕴含了点、线、面的对称、相等、平行、垂直等数量和位置关系,是展开空间想象的重要载体.
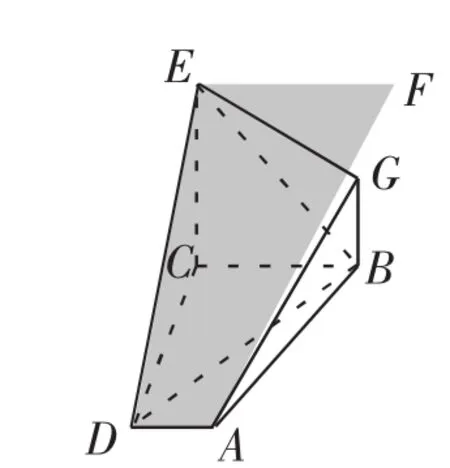
图10
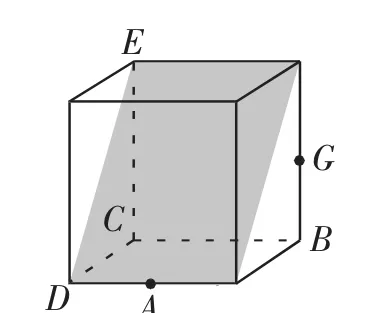
图11
为了突出长方体模型的重要作用,笔者拿前两天学生刚做过的一道高考题举例说明.
(2014·湖北卷文7)在如图12所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为()
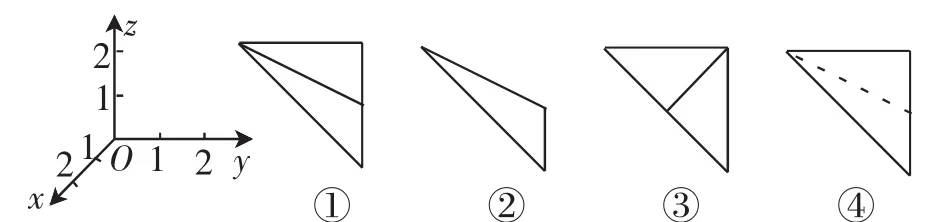
图12
A.①和②B.①和③C.③和②D.④和②
这道题与以往的三视图题目不同,以往的几何体大多数都是水平放置的,而这个四面体是架空在空间的,考查学生的空间想象能力.学生凭空去想,很难想象出这个几何体的形状和它的三视图,而借助正方体模型,如图13,有了三视图需要的几个投影面,和与这些面垂直、平行的线,三视图则迎刃而解.有学生感叹:我们没有空间想象的“火眼金睛”,然而何其有幸,我们有长方体模型.文[3]中也强调了长方体作为背景模型在解题中的奇效,利用长方体模型,提升了学生的空间想象能力.
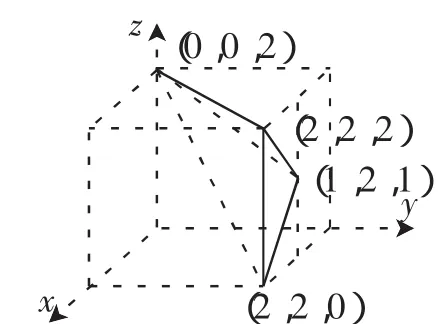
图13
在教学中遇见了错题,笔者并没有直接翻篇到下一题,也没有一带而过.笔者引导学生从数的角度对比了计算结果,利用几何画板,让学生从形的角度直观感受了原因,再上升到理论层面,给出理论支撑.讲完,学生感到很有收获.错题有错题的价值.通过这个题,学生认识到后续的复习应该多注意概念,也对长方体模型的工具作用有了更深刻的体会.
1.普通高中课程标准实验教科书数学必修2[M].北京:人民教育出版社,2007.
2.刘岳.一道中考错题的分析与启示[J].中学数学教学参考(中),2015(1-2).
3.金伟兵.题高一尺技高一丈——立体几何三视图、直观图新题“破题法门”[J].中学数学(上),2015(3).
