恰到好处:谈综合题命制中的增加层次——以2016年四川成都卷第28题为例
2016-11-24江苏省连云港市黑林中学许银银
☉江苏省连云港市黑林中学 许银银
恰到好处:谈综合题命制中的增加层次——以2016年四川成都卷第28题为例
☉江苏省连云港市黑林中学许银银
中考压轴题承载了区分选拔功能,命题组专家们常常要根据教学经验和大样本下学情的了解,设计出有难度、富有挑战的压轴题.值得多数人认同的压轴题风格是简洁好懂、富有生长、少算多思,又要严守国家课程标准的刚性要求.然而每年中考试卷出来之后,我们总能见到有些地区由于命题组的“个人喜好”,置教学导向和课标要求于不顾,无度链接高中解析几何的知识点,使得提前补充过高中阶段解析几何性质的考生“沾了大光”,而严守课标的师生陷入初中繁杂解法的构造与运算之中.本文关注一道2016年压轴题,先给出思路突破,再跟进命题商榷和变式打磨.
一、考题及思路突破
考题(2016年四川成都)如图1,在平面直角坐标系xOy中,抛物线y=a(x+1)2-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P、Q两点,点Q在y轴的右侧.
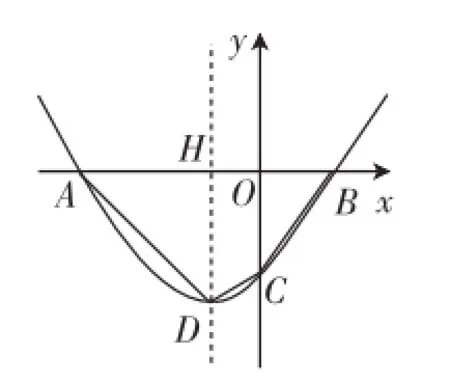
图1
(1)求a的值及点A、B的坐标.
(2)当直线l将四边形ABCD分为面积比为3∶7的两部分时,求直线l的函数表达式.
(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否成菱形?若能,求出点N的坐标;若不能,请说明理由.
思路突破:
(2)在进入面积比为3∶7的两部分的探索之前,先算出四边形ABCD的面积.由于抛物线的解析式在上一问中已明确为可很快确定顶点所以
接下来利用直线l将四边形ABCD分为面积比为3∶7的两部分,分析可知直线l只能与边AD或BC相交,所以有两种情况:①如图2,直线l与AD交于点M;②如图3,直线l与BC交于点M.
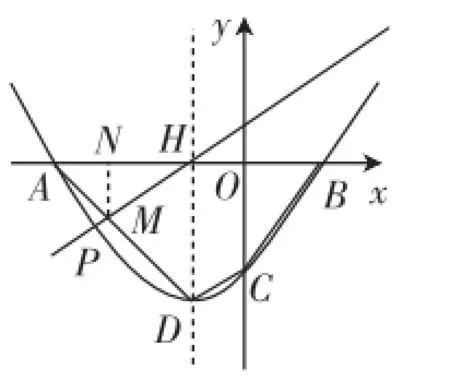
图2
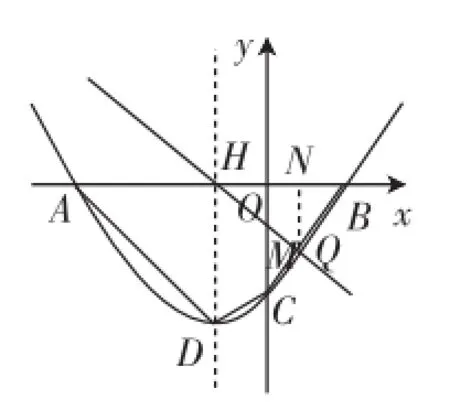
图3
由于直线l将四边形ABCD分为面积比为3∶7,所以其中一部分面积为四边形ABCD面积的即在图2或图3中,△AMH、△BMH的面积为3,即AH、BH边上的高为2.以下分类说明.
情况1:如图2,当直线l与AD交于点M时,过点M作MN⊥x轴于点N,由上面的分析,可得MN=2.利用MN∥DH带来的△AMN~△ADH,得比例式,可解得AN=2,ON=2,则M(-2,-2).设直线l的解析式为y=kx+b,由于l过M(-2,-2)、H(-1,0),则解得所以直线l的解析式为y=2x+2.
情况2:如图3,当直线l与BC交于点M时,过点M作MN⊥x轴于点N,则类似地,利用△BMN~△BCO,得,则所以所以设直线l的解析式为y=kx+b,由于l过H(-1,0),则解得即直线l的解析式为
另解反思:由上面的分析,还可将两种情况统一在图4中,作直线y=-2交AD、BC于M1、M2,这也是两个符合要求的点M.
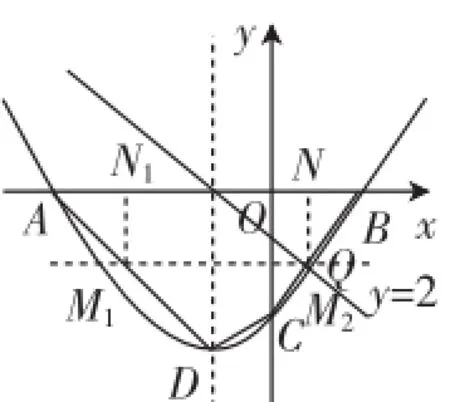
图4
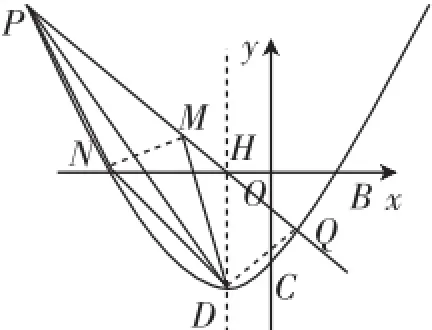
图5
(3)构造图5这样的可能的图形辅助分析.
由线段PQ的中点为M,四边形DMPN若为菱形,有DN∥=MQ.设直线ND的解析式为y=kx+b1,由D(-1,-3),得-3=-k+b1,所以b1=k-3,所以直线ND的解析式为y=kx+ k-3.由,解得xN=3k-1,即N(3k-1,3k2-3).
类似地,再设直线PQ的解析式为y=kx+b2.由H(-1,0),得y=kx+k.由得则x1+所以所以.再结合,可得xM-xN=xQ-xD,即解得所以所以.再验证发现,此时DN∥PM且四边形DMPN为菱形.
综上,以DP为对角线的四边形DMPN能成为菱形,当四边形DMPN为菱形时,点N的坐标为
另解思考:如图5,也可先从直线PQ的解析式入手,设P(x1,y1)、Q(x2,y2),且过点H(-1,0)的直线PQ的解析式为y=kx+b.-k+b=0,则b=k,则y=kx+k.由根据根与系数的关系,有x1+x2=-2+3k.y1+y2=kx1+k+kx2+k=3k2.由于点M是线段PQ的中点,所以根据中点坐标公式得点
假设存在这样的N点,则直线DN∥PQ.设直线DN的解析式为y=kx+k-3.
二、导向之思与命题商榷
静心演算之后,笔者深感这道试题的繁杂,根据多年教学经验,若非人群中前5%的优秀学生,要想在考场限时独立的背景下圆满解题是很难的.特别是第(3)问,如果熟悉高中阶段解析几何中的中点坐标公式、直线与抛物线交点的灵活处理等“高位知识”,则可以快速获得思路贯通,进入运算求解,使得“多想少算”的命题追求大打折扣.以下本着个人命题研究的兴趣,围绕该考题给出变式改编.
改编题:如图1,在平面直角坐标系xOy中,抛物线y= a(x+1)2-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点顶点为D.
(1)求四边形ABCD的面积;
(2)在抛物线的对称轴上取点G,当△BCG的周长最小时,求点G的坐标;
(3)设抛物线的对称轴与x轴交于点H,抛物线上有一点P,若直线PH将四边形ABCD的面积分成3∶7两部分,求点P的坐标.
改编意图:将原考题第(3)问删减,主要是原问过分链接拓展了高中阶段的解析内容,如果仅从初中阶段教材上的解法来处理,又显得力量不够.而将原题的第(2)问进行适度放开,使得点P有4个可能的位置,也达到了区分选拔的功能.
三、结束语
综合题命制是一个经典话题,初中数学考卷解答题的最后一道通常是大综合,往往选择一个开阔的平台,融入一些新的数学概念或性质,渐次生长,拓展挑战,供高层次学生展示解题实力.就本文想表达的观点来看,在增设条件或增加解题层次时,一定要注意恰到好处,而不能陷入“恶性生长”的无度地步,那样既影响了试题的内容效度,也影响教学导向和数学面貌.从这个意义上说,兹事体大,而非细节,也非小事,不容忽视.
1.王东.从“形聚”到“神似”:大题命制的一种追求——2016年盐城卷第28题思路突破与命题反思[J].中学数学(下),2016(9).
2.周红娟.开放与放开:概念生成与例题变式的教学追求——从“三角形内角和”教学说起[J].中学数学(下),2016(8).Z
