新定义曲线问题的创新解答

☉湖南省长沙市周南中学　张璐瑶

新定义曲线问题的创新解答

☉湖南省长沙市周南中学张璐瑶

以新定义为背景的高考命题屡见不鲜，此类问题不仅能有效考查考生对基础知识的掌握程度，而且对考生的创新能力和应用能力提出了更高的要求.解题此类问题时要彻底理清“新定义”的内涵，结合相关知识加以灵活处理.下面以一类新定义曲线问题为例，就问题的创新解答进行分析.

一、题目展示

引例曲线C是平面内与三个定点F1（-1，0），F2（1，0）和F3（0，，1）的距离的和等于的点的轨迹.给出下列四个结论：

①曲线C关于x轴、y轴均对称；

②曲线C上存在一点P，使得|PF3|=

③若点P在曲线C上，则△FPF面积的最大值是1；

④△PF2F3面积的最大值为

其中所有真命题的序号是__________.

命题意图：命题中定义一个新的概念，能有效考查学生即时学习的能力、培养学生的创新意识.对于解析几何问题，可从数（方程）与形（曲线）两个角度来认识事物，这两种方式互为补充.

二、创新解答

1.把握新定义原理，直奔主题

新定义曲线是平面内与三个定点的距离的和等于定值的点的轨迹，因此可直接设出动点坐标结合两点间距离公式得出曲线方程.

设曲线C上任意一点坐标为P（x，y），由题意可知C的方程为

2.把握相关原理，间接判断

对于①，判断一个陌生曲线的对称性问题，我们不易画出曲线的图像，所以利用对称性的定义是首选策略.

在此方程中，用-x，-y分别取代x，y，可知C只关于y轴对称，不关于x轴对称.故①错.

同理判断一条曲线是否关于某条直线对称，设直线为x=a，通过验证f（2a-x）与f（x）的关系来实现.

判断某点是否为曲线的对称中心，设点坐标为（a，b），可通过验证F（2a-x，2b-y）与F（x，y）之间的关系来实现.

3.把握问题本质直接判断

对于②，若|PF3|=，故②错.

对于④，此时需要先考虑以F2，F3为焦点，实半轴为的椭圆E，其短轴顶点到直线F2F3：x+y-1=0的距离为.此时△PF2F3的面积为但是曲线C应该在此椭圆内部，所以△PF2F3的面积应小于.故④正确.

三、变式演练

变式1曲线C是平面内到定点A（1，0）的距离与到定直线x=-1的距离之和为3的动点P的轨迹，则曲线C与y轴交点的坐标是______；又已知点B（a，1）（a为常数），那么|PB|+|PA|的最小值d（a）=_______.

（2）由（1）可知y2=

如图1所示，令y=1，则10x+ 15=1或-2x+3=1，解得x=-或1.

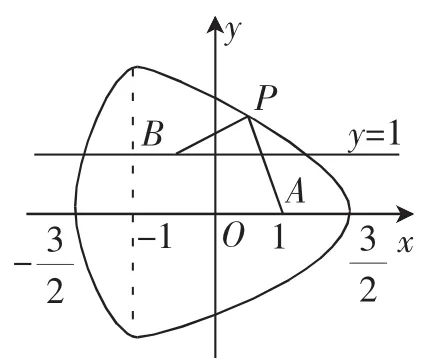
当-1＜a＜1时，直线y=1与y2=-2x+3于点P，满足|PB|+|PA|取得最小值.所以此抛物线的准线为x=2，即直线y=1与准线的交点Q（2，1），此时d（a）= |QB|=2-a.

点评：本题以新定义曲线为背景综合考查了抛物线的定义和性质、直线与抛物线相交问题、两点间距离公式等基础知识与基本技能，考查了分类讨论的思想及推理计算能力.

变式2曲线C是平面内与定点F（2，0）和定直线x= -2的距离的积等于4的点的轨迹.给出下列四个结论：

①曲线C过坐标原点；

②曲线C关于x轴对称；

③曲线C与y轴有3个交点；

其中，所有正确结论的序号是___________.

解析：设点P的坐标为（x，y）.因为曲线C是平面内与定点F（2，0）和定直线x=-2的距离的积等于4的点的轨迹，所以因为当x=0时，y=0，故曲线C过坐标原点，故①正确.

令x=0时，y=0，故曲线C与y轴只有1个交点，故③不正确.

点评：解析几何的本质是用代数方法研究几何性质，为了研究曲线的性质，首先要按定义求出曲线方程.再结合曲线的相关性质及题目的隐含条件，即可顺利求解.

变式3在平面直角坐标系中，动点P（x，y）到两条坐标轴的距离之和等于它到点（1，1）的距离，记点P的轨迹为曲线W.

（Ⅰ）给出下列三个结论：

①曲线W关于原点对称；

②曲线W关于直线y=x对称；

③曲线W与x轴非负半轴，y轴非负半轴围成的封闭图形的面积小于，化简得|xy|+x+y=1，用（-x，-y）代替方程中的（x，y）所得方程与原方程不相同，因此①错误.

把原方程中x，y互换，方程不变，因此曲线关于直线y=x对称，故②正确.

其中，所有正确结论的序号是_____.

（Ⅱ）曲线W上的点到原点距离的最小值为______.

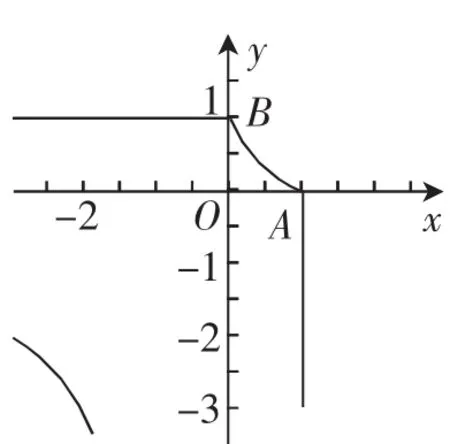
图2　

点评：化生为熟是解决创新问题的基本策略，本题按定义求出曲线方程，再利用分类讨论思想得出不同区间内曲线的不同形状，进而得出所求结论.