基于CQPSO的LCL滤波器设计方法

师文芳,陈　华,廖俊勃

(新疆大学 电气工程学院,新疆 乌鲁木齐 830047)



基于CQPSO的LCL滤波器设计方法

师文芳,陈华*,廖俊勃

(新疆大学 电气工程学院,新疆 乌鲁木齐 830047)

针对光伏并网逆变系统中LCL滤波器参数设计的困难,提出采用混沌量子粒子群算法对滤波器参数进行寻优．利用混沌优化方法具有的随机性、有界性、遍历性等特性,来扩大算法的搜索范围和提高收敛速度．对LCL滤波器进行分析后,确定约束条件,结合算法来对其参数进行优化设计．对三相光伏并网逆变器进行仿真实验,将混沌量子粒子群算法与自适应遗传算法进行比较,结果表明该算法比自适应遗传算法有更好的滤波效果,谐波畸变率也更小．

并网逆变器;混沌;量子粒子群;LCL滤波器

太阳能由于无污染、取之不尽用之不竭等优点已成为理想的绿色环保能源．但在光伏发电系统中,并网逆变器会将高次谐波含量带入电网,从而造成电网不稳定．目前普遍采用在电网侧接入滤波器来抑制这些谐波．从现阶段工业应用情况来看,在小功率并网逆变器中一般采用L滤波器[1],就可以达到很好的滤波效果．在中、大功率并网逆变器中一般采用LCL滤波器[2],LCL滤波器是基于L滤波器的改进．要达到相同的滤波效果,LCL滤波器的电感要比L滤波器的电感小得多,从而减小了滤波电感的体积,降低了滤波器的成本,而且还提高了系统的动态性能．但由于LCL滤波器各参数之间联系紧密,且设计滤波器时需要考虑成本、体积、滤波效率等因素,所以很难保证最终设计结果达到全面最优．

近年来,很多学者对LCL滤波器的设计方法进行了研究．Liserre等[3]对LCL滤波器在参数选择时应遵循的限制条件及设计步骤做了详细说明,但是此方法需要多次尝试且计算过程繁琐,在实际工程中并不实用．张宪平等[4]提出了一种新型LCL滤波器设计方法,将谐振频率作为中间参数,通过对两个不对称电感比例的二次方程求解,从而得到滤波器的各个参数,但此设计归根到底也用到了一个反复凑解方法．邵文权等[5]提出了基于自适应遗传算法来优化LCL滤波器参数,但以开关频率处谐波衰减率为优化目标,导致了参数设计过大,提高了成本,不利于工程实现．因此,研究LCL滤波器参数优化的方法,不仅有利于提高滤波器参数设计的准确性,而且能进一步优化滤波器的性能．针对现有大功率光伏发电逆变器系统中LCL滤波器参数设计存在的计算复杂、准确性低、滤波性能差等不足,笔者在综合考虑滤波器总电感、电容、谐振频率及滤波效果的基础上,采用混沌量子粒子群算法(CQPSO)计算滤波器参数．

1　LCL滤波器的滤波性能分析

图1所示为带LCL滤波器的光伏发电系统的结构图．图1中PV为光伏阵列,C1为输入直流侧的滤波电容;S1～S6为三相逆变桥的6个IGBT开关管,开关管在通断时会产生高次谐波;L1和L2分别为逆变侧和电网侧电感,由于电感上的电阻非常小,该文忽略其电阻;对A相来说，L1A、CA和L2A共同组成3阶LCL滤波器．

图1　带 LCL 滤波器的光伏发电系统结构Fig.1　Structure of photovoltaic power generation system with LCL

文献[5-6]中对LCL滤波器的性能和参数做了详细的分析, 笔者将其中对总电感(LT=L1+L2)、滤波电容和谐振频率的约束条件作为该文的设计条件,即

总电感

(1)

其中:ΔImax为最大的纹波电流；Emp为电网相电压峰值；Imp为电网相电流峰值．

滤波电容

(2)

其中:Un为电网相电压有效值．

谐振频率

(3)

其中:fs为电网频率；fsw为开关频率．

2　混沌量子粒子群算法

2.1量子粒子群算法

粒子群算法(particleswarmoptimization,简称PSO)是一种模拟鸟群捕食的智能算法,每个粒子根据适应度函数确定个体的最优位置和整个种群的全局最优位置,不断迭代来达到寻优的目的[7]．该算法具有原理简单、参数少、收敛快等特点,但PSO的搜索范围受限,局限于全局最优点和局部最优点．因此有学者提出了量子粒子群算法 (quantumbehavedparticleswarmoptimization, 简称QPSO)[8],将量子计算与PSO结合,不仅使其保留了PSO的优点,也提高了计算效率,使得QPSO在求解优化问题时有很好的效果．

在QPSO算法中,由于不能同时确定粒子个体的位置和速度,故要引入波函数ψ,其中|ψ|2代表了粒子位置的概率密度,即

|ψ|2dxdydz=Qdxdydz,

(4)

其中:Q为概率密度函数,且其满足

(5)

粒子位置通过MonteCarlo随机模拟的方式得到,相关表达式为

(6)

其中:Pb为粒子的个体最优位置;Pg为种群的全局最优位置;θ和μ为在[0,1]上服从均匀分布的随机数;P(t)为粒子在第t次迭代的势阱;X(t)为粒子的位置;L为粒子与种群平均最优位置的带权距离,表达式为

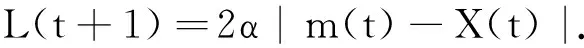
(7)

式(7)中α为压缩-扩张因子[9],用来控制粒子的收敛速度,参数m(t)是种群中所有粒子的个体最优位置的平均值,2个参数取为

(8)

其中:N表示种群的大小;tmax为迭代的最大次数;当μ≤0.5时,α取正;当μ>0.5时,α取负．

根据式(6)～(8),可以得到

(9)

粒子的个体最优位置Pbi更新方式如下

(10)

全局最优位置的Pg更新方式如下

(11)

其中:函数f(·)为目标函数．

2.2混沌量子粒子群算法

QPSO已比PSO具有更好的性能,但是在迭代后期易陷入局部最优、收敛速度变慢、寻优精度差．针对这些缺点,笔者提出采用混沌量子粒子群算法(CQPSO)对滤波器参数进行寻优．

混沌运动是一种非线性系统中有界的、不稳定的动态行为,在确定条件下具有一定的规律性.混沌理论[10-11]指出“混沌意味着随机变化”、“混沌是非周期的有序性”．混沌运动的不重复性,可使其按照自身的搜索运动来进行全局搜索．这样的特性为解决QPSO的缺点提供了思路,利用混沌运动可以避免陷入局部寻优、增强搜索范围、加快收敛．

一般采用Tent映射来产生混沌序列[12-14]．Tent映射的表达式如下

(12)

其中:xk为第k个粒子在混沌空间中的位置．经过式(12)的迭代,生成混沌变量,然后使用

(13)

进行线性变换．

在整个算法中有一个很重要的函数需要建立,其为适应度函数．该文以三相并网逆变器中LCL滤波电路为研究对象,进行参数设计,为使设计结果的滤波效果较好,即谐波衰减率较小,参考文献[6]将适应度函数定义为

(14)

其中:Q为电压的有效值,Q1为电流基波的有效值．

CQPSO的具体流程如下:

(1) 对QPSO粒子数种群大小、变量个数等相关参数进行初始化,利用Tent映射(式(12))产生混沌随机序列,并用公式(13)将混沌变量线性变换到搜索区间,对粒子速度和位置进行初始化．

(2) 使用适应度函数对每个粒子的位置进行评价,并同其所经历过的最佳值进行比较,如果较好,则以新的位置取代粒子的最佳值,反之则最佳值不变．

(3) 如果达到了混沌搜索次数,则执行(4),否则执行(2)．

(4) 达到结束条件,输出最优解．

3　仿真实验

在MATLAB的Simulink环境下搭建如图2所示的系统仿真模型,进行仿真研究,来验证所采用的混沌量子粒子群算法寻优的可行性．在模型中, Udc=150V,C1=560F,电网负载功率为1 000W．

图2　系统仿真模型Fig.2　System simulation model

在CQPSO中,设置粒子群大小为30,α=0.5 ～1.0,最大迭代次数T=100．为了进一步说明该文采用算法的高效性,用文献[5]提出的自适应遗传算法作为比较对象,运行程序得到两种算法下的LCL滤波器的各个参数,即逆变侧电感L1、网侧电感L2和滤波电容C的值,结果如表1所示．

表1　CQPSO与自适应遗传算法的LCL滤波器参数比较

将上述两种算法下所得的LCL参数代入仿真模型,得到各自的网侧电流波形如图3所示．

图3　2种算法下网侧电流波形Fig.3　Grid side current waveform of two methods

由图3可直观看出,在自适应遗传算法下,并网电流虽然在一个周期内可以实现稳定控制,但电流正弦度较差,控制效果并不十分理想．采用CQPSO所得到的参数,不仅可以快速实现并网电流的稳定控制,而且具有良好的动态性能,控制效果理想．

为了进一步验证CQPSO所设计的LCL滤波器的滤波性能,经计算可得各自对应的网侧电流频谱如图4所示．

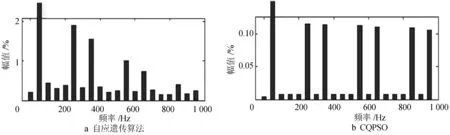
图4　2种算法下网侧电流频谱图Fig.4　FFT results of two methods

由图4可以算出,自适应遗传算法优化得到的LCL滤波器滤波后的电流THD为3.55%,而CQPSO优化得到的LCL滤波器滤波后的电流THD仅为0.44%,谐波畸变率明显减小．

图5为A相并网电流和电网电压的关系图．图5中振幅小的正弦曲线为A相并网电流,振幅大的正弦曲线为并网电压．

图5　A相并网电流和电网电压的关系图Fig.5　The relationship between current and grid voltage network of A phase grid current

由图5可以看出,并网电流与电网电压保持同频同相,并网逆变器实现了单位功率因数并网运行,这进一步证明了混沌量子粒子群算法在优化LCL滤波器参数中的可行性和高效性．

4　结束语

在对三相并网逆变器LCL滤波器滤波性能分析的基础上,针对其参数设计存在的计算复杂、准确性低等问题,提出采用混沌量子粒子群算法对滤波器参数进行寻优．为了验证所采用算法的可行性和高效性,搭建模型进行仿真实验,并与自适应遗传算法进行比较．仿真结果表明,混沌量子粒子群算法下得到的LCL滤波器参数具有更好的滤波效果,谐波畸变率(THD)也更小．采用混沌量子粒子群算法优化LCL滤波器参数,设计方法简单、可靠性强,对LCL滤波电路的设计有很好的应用价值．

[1]YANGC,SMEDLEYKM.One-cycle-controlledthree-phasegridconnectedinvertersandtheirparalleloperation[J].IEEETransactionsonIndustrialApplications, 2008, 44 (2): 663-671.

[2]WANGTC,YEZH,GAUTAMS,etal.Outputfilterdesignforagrid-interconnectedthree-phaseinverter[C]//IEEEPowerElectronicsSpecialistsConference, 2003: 779-784.

[3]LISERREM,BLAABJERGF,HANSENS.DesignandcontrolofanLCL-filter-basedthree-phaseactiverectifier[J].IEEETransactionsonIndustryApplications, 2005: 41 (5): 1281-1291.

[4]张宪平, 李亚西, 潘磊, 等. 三相电压型整流器的LCL型滤波器分析与设计[J]. 电气应用, 2007, 26 (5): 65-68.

[5]刘飞, 查晓明, 段善旭. 三相并网逆变器LCL滤波器的参数设计与研究[J]. 电工技术学报, 2010, 25 (3): 110-116.

[6]邵文权, 宋江喜, 程远, 等. 基于自适应遗传算法的风力发电系统网侧LCL滤波器的优化设计[J]. 电力系统保护与控制, 2013, 41 (21): 116-121.

[7]SELVAKUMARAI,THANUSHKODIK.Anewparticleswarmoptimizationsolutiontononconvexeconomicdispatchproblems[J].IEEETransactionsonPowerSystems, 2007, 22 (1): 42-51.

[8]SUNJ,FENGB,XUW.Particleswarmoptimizationwithparticleshavingquantumbehavior[C]//CongressonEvolutionaryComputation, 2004: 325-329.

[9]黄泽霞, 俞攸红, 黄德才. 惯性权自适应调整的量子粒子群优化算法[J]. 上海交通大学学报 (自然科学版), 2012, 46 (2): 228-232.

[10]陈滨. 混沌波形的相关性-相空间轨迹与混沌序列自相关特性[M]. 西安: 西安电子科技大学出版社, 2011.

[11]陈奉苏. 混沌控制及其应用[M]. 北京: 中国电力出版社, 2006.

[12]单梁, 强浩, 李军. 基于Tent映射的混沌优化算法[J]. 控制与决策, 2005, 20 (2): 179-182.

[13]张学良, 温淑花, 李海楠, 等. 基于Tent映射的混沌粒子群优化算法及其应用[J]. 中国机械工程, 2008, 19 (17): 2108-2112.

[14]王瑞琪, 张承慧, 李珂. 基于改进混沌优化的多目标遗传算法[J]. 控制与决策, 2011, 26 (9): 1391-1397.

(责任编辑郑小虎)

LCLfilterdesignmethodsbasedonchaosquantumparticleswarmoptimization

SHIWenfang,CHENHua*,LIAOJunbo

(SchoolofElectricalEngineering,XinjiangUniversity,Urumqi830047,China)

BecausethedesignofLCLfilterofPVgrid-connectedinvertersystemwasverydifficult,chaoticquantumparticleswarmoptimizationalgorithm(CQPSO)wasusedtooptimizethefilterparametersinthispaper.Thechaosoptimizationmethodwiththecharacteristicsofrandomness,boundednessandergodicitycouldimprovethesearchscopeandconvergencerateofthequantumparticleswarmoptimization.AftertheanalysisofLCLfilter,theparametersofLCLfilterweredesignedandoptimizedbyCQPSOwithdecidedconstraints.Comparedwiththeadaptivegeneticalgorithm(AGA),theresultsfromsimulationexperimentofthethree-phasephotovoltaicgrid-connectedinvertershowedthattheCQPSOhadabetterfilteringeffectandsmallerTHD.

gridinverter;chaotic;quantumparticleswarm;LCLfilter

10.3969/j.issn.1000-2162.2016.02.012

2015-10-28

师文芳(1988-),女,陕西咸阳人,新疆大学硕士研究生;*陈华(通信作者),新疆大学副教授,硕士生导师,E-mail:xj-chenhua@163.com.

TM615

A

1000-2162(2016)02-0067-06