求解非线性方程组的一类非单调修正Levenberg-Marquardt算法

郭　楠,黄华鹰

(1.南京工程学院 数理部,江苏 南京　211167; 2.安徽大学 数学科学学院,安徽 合肥　230601)



求解非线性方程组的一类非单调修正Levenberg-Marquardt算法

郭楠1,黄华鹰2

(1.南京工程学院 数理部,江苏 南京211167; 2.安徽大学 数学科学学院,安徽 合肥230601)

通过将非单调搜索准则与修正Levenberg-Marquardt(L-M)算法结合,提出了求解非线性方程组的一个新的非单调修正L-M方法.新算法在每次迭代步都引入校正步,使新的试探步更靠近Moore-Penrose步.利用信赖域技巧修正L-M参数,在一定的条件下,证明了该算法的全局收敛性.数值试验表明了算法的有效性.关键词:非线性方程组；Levenberg-Marquardt方法；非单调；信赖域方法；收敛性

考虑下述约束非线性方程组

(1)

其中:F:Rn→Rm二次连续可微的函数.在论文中,总假设(1)的解集非空,记作X*.

与非线性方程组(1)相关的最优化问题为

minf(x),

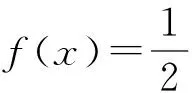
求解非线性方程组目前有许多有效的方法[1-3],其中,Levenberg-Marquardt方法是解决(1)的经典方法之一,利用如下线性方程组的解dk作为点xk处的一个搜索方向

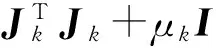
文[4]中提出的修正L-M算法是单调下降的.但是对于一些函数单调算法并不理想,收敛速度较慢.而非单调算法不需要每一步都单调下降,1993年,邓乃扬[5]首次提出了一类具有强收敛性质的非单调信赖域算法,试验结果表明适当的非单调算法比单调算法有更好的收敛结果.由于非单调技术具有很好的计算效果,很多学者对它进行了进一步的研究,并被成功地应用到很多优化算法中[5-8].Mo和Gu在文[6]中提出了一种非单调搜索技术获得了较好的数值效果,即

其中

(2)

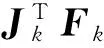
1　算　法

首先给出利用信赖域技巧的非单调修正L-M算法.

定义(1)的价值函数为

则在第k步迭代的实际下降量和预估下降量分别为

算法1(非单调修正L-M算法)

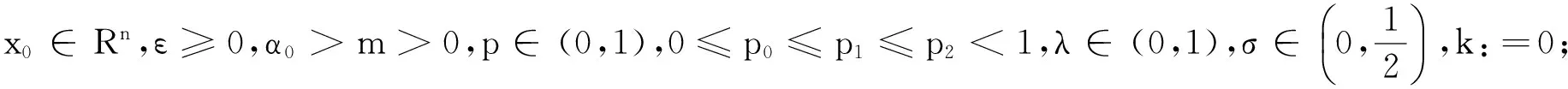
得到dk,求解

得到sk;

步4:置xk+1=xk+sk,若rk≥p0,并转步5;否则,令ik是满足下面不等式的最小非负整数i,

(3)

令tk=λik,xk+1=xk+tksk;

步5:计算

k:=k+1,转步2.

在算法1中,m为一给定常数,它是参数因子αk的下界.当迭代点靠近方程组的解时,它防止试探步过大而引起的数值困难.

显然,L-M步dk是下面最值问题的解

若定义

则dk也是下面信赖域问题的一个解

由Powell在文[10]中给出的结果

(4)

(5)

注意到

从而,预估下降量满足

(6)

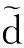
及

(7)

因此,有

(8)

此外,结合(4)～(8)式,可以得到如下引理：

引理1设sk由算法1的步2产生,则∀k≥1,下式成立

(9)

且

(10)

2　算法的收敛性

为分析算法的收敛性,作如下假设:

(AS1) 水平集L={x|f(x)≤f(x0)}⊂Ω,其中Ω是空间中的Rn有界闭集.

(AS3)F(x),J(x)在水平集L上是Lipschitz连续,即存在正数L1和L2,使得

由于J(x)的Lipschitz连续性,有

(11)

为了证明算法的适定性,首先给出如下引理:

引理2设{xk}是由算法1产生的序列,则对任意的k≥0,都有

fk+1≤Dk+1.

证明设I={k:rk≥p0},J={0,1,2,…}I.当k∈I时,有

结合引理1,有

得Dk≥fk+1.

当k∈J时,由(3),(10)式,有

得Dk≥fk+1.

从而,∀k≥0,都有Dk≥fk+1.又由Dk的定义,对∀k≥0,有

下面证明算法1的步4是适定的,从而算法是适定的.

引理3对任意的k∈J,算法1的步4的线搜索是有限终止的.即存在正整数ik使得(3)式成立.

证明假设步4不能有限终止,则存在k∈J,满足

由于Dk≥fk,可得

又有f的可微性,不等式两边令i→∞并取极限,有

引理4设假设(AS1)、(AS2)成立,{xk}是由算法1产生的序列,则存在正数M,使得步长tk满足

证明由算法1的步4,有

通过泰勒展式得到,∃ξk∈(xk,xk+λ-1tksk),使得

又由F的二阶连续可微性知,∃M>0,使得

结合引理2及上面的式子,有

由引理1可得

整理得

综合上面两式及(AS2),有

引理5设假设(AS1)成立,算法1产生的序列{xk}和{Dk},满足{xk}⊂L且{Dk}非增且收敛.

证明先用归纳法证算法产生的序列{xk}⊂L.

当k=1,显然成立.现假设xk∈L,即f(xk)≤f(x1).由Dk+1的定义知Dk+1≤f(x1),结合引理2知f(xk+1)≤f(x1).

下证{Dk}是单调下降的.

当k∈I时,由算法1及(9)式，有

所以,有

当k∈J时,由算法1、引理4及(10)式,有

(12)

由Dk的定义及(12)式,有

所以,序列{Dk}是单调下降的.又Dk≥0,则序列{Dk}是收敛的.

接下来,证明算法1的全局收敛性.

定理1设假设(AS1)及(AS3)成立,{xk}是由算法1产生的序列,则有

证明若定理不成立,则存在ε>0,使得

(13)

由F的二阶连续可微性知,∃β>0,使得

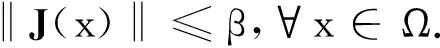
又根据引理5的证明可知,∀k≥0,有

因为{Dk}是收敛的,所以，有

可推得

由sk的定义和算法1,推得

(14)

另一方面,结合引理1、(11)和(13)式,有

根据引理2,有

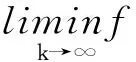
3　数值结果

为了验证算法1的有效性,对一些奇异问题进行了数值试验,并与文[11]的传统L-M算法进行了比较,结果列于表1、2.测试问题来自文[12].表1是对文[5]的标准问题修改得到的(见文[11]的算例说明)，表2是文[12]的Powell奇异问题.

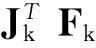
表1　其余测试问题的数值结果

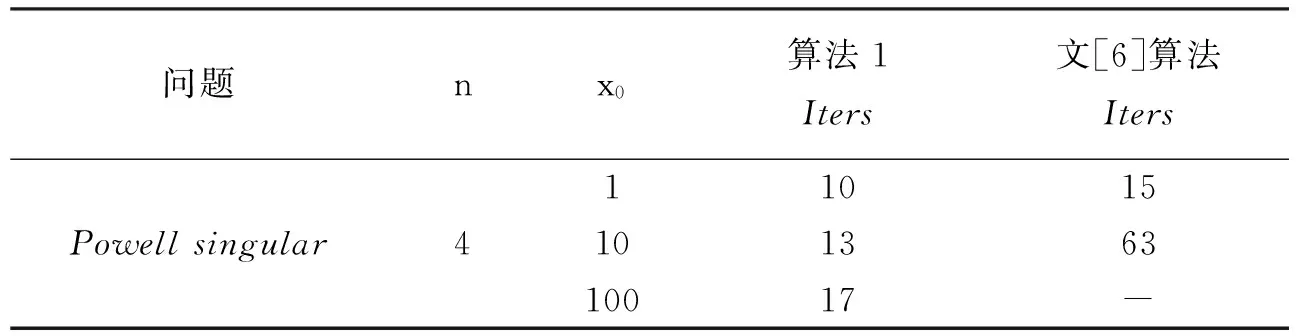
表2　 Powell奇异问题的数值结果

4　结束语

[1]FANJY,PANJY.Animprovedtrustregionalgorithmfornonlinearequations[J].ComputOptimAppl, 2011, 48 (1): 199-210.

[2]HAGERW,ZHANGH.Self-adaptiveinexactproximalpointmethod[J].ComputOptimAppl, 2008, 39: 161-181.

[3]蒋利华,马昌凤.光滑阻尼Gauss-Newton法解非线性不等式组[J].安徽大学学报(自然科学版), 2009, 33 (1): 18-21.

[4]FANJY,ZENGJL.ALevenberg-Marquardtalgorithmwithcorrectionforsingularsystemofnonlinearequations[J].AppliedMathematicsandComputation, 2013, 219 (17) : 9438-9446.

[5]DENGNY,XIAOY,ZHOUFZ.NonmonotonictrustregionaIgorithm[J].OptimiTheoryAppl, 1993, 76 (2): 259-285.

[6]GUNZ,MOJT.Incorporatingnonmonotonestrategiesintothetrustregionmethodforunconstrainedoptimization[J].ComputersandMathematicswithApplications, 2008, 55 (9): 2158-2172.

[7]GRIPPOL,LAMPAXIELLOANDF,LUCIDIS.AtruncatedNewtonmethodwithnonmonotonelinesearchforunconstrainedoptimization[J].JournalofOptimizationTheoryandApplications, 1989, 60: 401-419.

[8]SHIZJ,WANGSQ,XUZW.Theconvergencegradientmethodwithnonmontonelinesearch[J].AppliedMathematicsandComputation, 2010, 217 (5): 1921-1932.

[9]杨柳,陈艳萍.求解非线性方程组的一种新的全局收敛的Levenberg-Marquardt算法[J].计算数学, 2008, 30 (4): 388-396.

[10]POWELLMJ.Aniterativemethodforfindingstationaryvaluesofafunctionofseveralvariables[J].ComputJ, 1962, 5: 147-151.

[11]杨柳,陈艳萍.一种新的Levenberg-Marquardt算法的收敛性[J].计算数学, 2005, 27 (1): 55-62.

(责任编辑朱夜明)

A nonmonotonic L-M method with correction for solving nonlinear equations

GUO Nan1, HUANG Huaying2

(1.Department of Mathematics and Science,Nanjing Institute of Technology,Nanjing 211167,China;2.School of Mathematical Sciences,Anhui University,Hefei 230601,China)

In this paper,by using the nonmonotonic techniques and modified L-M method,we proposed a new nonmonotone L-M algorithm with correction for solving nonlinear equations.At every iteration, not only a L-M step but also a modified step was computed which makes the trial step closer to the Moore-Penrose step.On the other hand,the L-M parameter was updated by the trust region technique.Under certain conditions,we proved global convergence of this new method.Numerical results show that this new method performs very well.

nonlinear equations;Levenberg-Marquardt method;nonmonotone;trust region method;convergence

10.3969/j.issn.1000-2162.2016.02.003

2015-01-06

国家自然科学基金资助项目(61305072);江苏省高校自然科学研究基金资助项目(13KJB110011);南京工程学院校级科研基金资助项目(QKJB201310)

郭楠(1983-),女,江苏靖江人,南京工程学院讲师.

O221.2

A

1000-2162(2016)02-0014-07