基于变比连续化的风电系统OLTC电压控制灵敏度算法
2016-09-20王艳艳李生虎雷庆坤董王朝
王艳艳,李生虎*,雷庆坤,董王朝
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.国网安徽省电力公司检修公司,安徽 合肥 230061)
基于变比连续化的风电系统OLTC电压控制灵敏度算法
王艳艳1,李生虎1*,雷庆坤2,董王朝1
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.国网安徽省电力公司检修公司,安徽 合肥 230061)
风电功率快速变化导致电压波动频繁且幅度较大.有载调压变压器(on-loadtapchanger, 简称OLTC)通过改变无功分布实现调压,无需新增投资.普通变比灵敏度算法未考虑变比的离散约束,所得灵敏度不很准确,用于指导OLTC变比调节存在误差.采用二进制编码,将变比转化为0-1变量的线性组合,引入NCP函数将0-1变量连续化,提出基于NCP函数的连续化变比灵敏度算法,以应用于风电系统电压控制.探讨分析影响OLTC变比调节的因素.算例分析表明该文算法是有效可行的.
风电波动;有载调压变压器;电压控制;灵敏度;离散变量;NCP函数
大规模风电并网后,风速波动幅度和频率都比负荷波动更为严重[1].当风电机组按恒功率因数运行、无功出力随有功变化时,就会出现电压波动甚至越限,此需要予以调节.调节手段有固定/可控并补、常规/风电机组等[2-3].固定并补装置成本低,但灵活性差;可控并补装置响应速度快,但成本较高;常规/风电机组调压范围较小.在无功充足的电网中,通过调节有载调压变压器(on-loadtapchanger, 简称OLTC)变比来改变无功分布,无需新增投资即可灵活实现调压,且调节范围较宽.
OLTC变比调节的算法包括优化和灵敏度算法[4].前者能得到变比最优值,但不能反映次优结果,计算量大[5-7];后者可得到灵敏度指标、变比调节的最优和次优结果,计算量较小,但容易计及调节约束[8-9].这两种算法,都不可回避变比离散这一难题.采用摄动法计算灵敏度,虽然容易计及变比离散性,但是需多次潮流计算,在线应用效率不高.将变比视为连续变量,然后将计算结果取整,虽然易于实现,但对含多个OLTC的系统,结果偏差较大甚至不正确.
离散变量连续化处理,为OLTC变比调节提供了新思路.NCP函数具有连续、光滑、可微等特征,常用于处理离散变量和不可微,是一种应用较为广泛的连续化方法[10-11].文献[12-13]先忽略离散约束,快速确定离散变量上下界,以上下界构造互补约束条件,再经光滑的NCP函数转化为等价光滑方程组,但离散变量解不全在上下界内.对于等间距离散变量,文献[14]采用二进制编码,将其转换为若干0-1变量的线性组合,避免限制其于某一特定上下界内.目前离散变量连续化方法,多应用于非线性混合整数无功优化,在灵敏度分析方面尚未见相关报道.笔者将连续化方法应用于OLTC变比的灵敏度分析,以实施风电系统电压控制.采用二进制编码将变比转化为0-1变量的线性组合,引入NCP函数将0-1变量连续化,提出基于NCP函数的连续化变比灵敏度算法,并探讨分析影响OLTC变比调节的因素.最后通过算例分析验证其有效性.
1 基于灵敏度指标的OLTC变比调节
1.1普通变比灵敏度算法
为研究OLTC变比变化对节点电压的影响,按下式扩展雅克比矩阵[15]
(1)
其中:P和Q为有功和无功向量;θ和V为电压相角向量和幅值向量;k为变比向量;J为雅可比矩阵.
令ΔP=ΔQ=0,由式(1)可得
(2)
则节点电压对变比的灵敏度矩阵为
(3)
设节点i电压越限量为ΔVi,j号OLTC的变比调节量为
(4)
其中:f是取整函数,可四舍五入(round函数)、向上取整(ceil函数)及向下取整(floor函数);ΔTcj=ΔVi/(Sijkj0)为j号OLTC分接头调节量计算值;kj0为j号OLTC变比步长.
1.2风电系统OLTC电压控制步骤
以电压越下限为例,分接头每调节1档记为动作1次,日最大允许动作次数为Nmax[16],截至当前j号OLTC累计动作次数为Nj,变比每次最大调节量为Δkjmax,上次调节时刻为tj,最小调节时间间隔为Δtmin,当前时刻为tpresent.风电系统中OLTC电压控制步骤为:
(1) 根据Nmax和Δtmin(同一时段,不计Δtmin约束)确定当前可调的OLTC,m为可调OLTC的总数,若m=0,转(6),否则执行(2).
(2) 确定越限量最大的节点电压Vi,将Vi对可调OLTC变比灵敏度的绝对值降序排列,各OLTC按相应的排序编号为1, 2, …,m,1号OLTC调节Vi最有效,2号OLTC次之,以此类推.
(3) 选择最有效的OLTC,即置j=1,按式(4)计算Δkj,若Δkj=0,转(6),否则执行(4).
(4) 若|Δkj|≤Δkjmax,Nj≤Nmax,则Δkj不变,否则将Δkj置为最大允许调节量(Δkj正负保持不变).
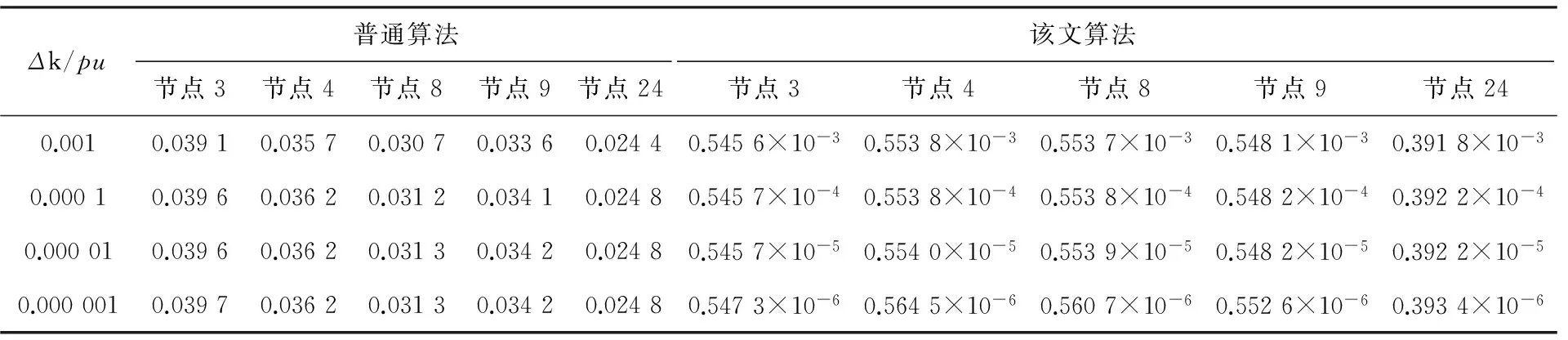
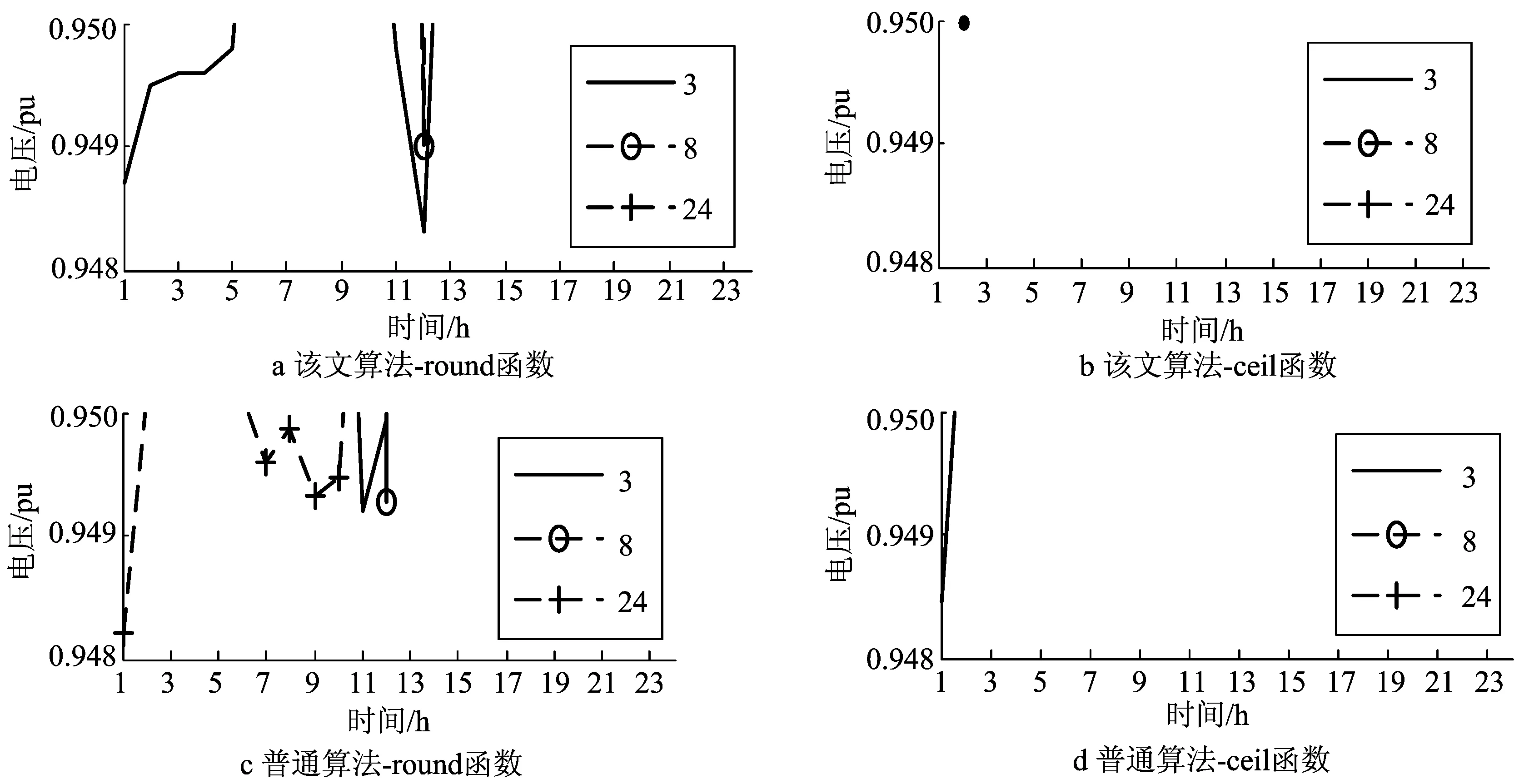
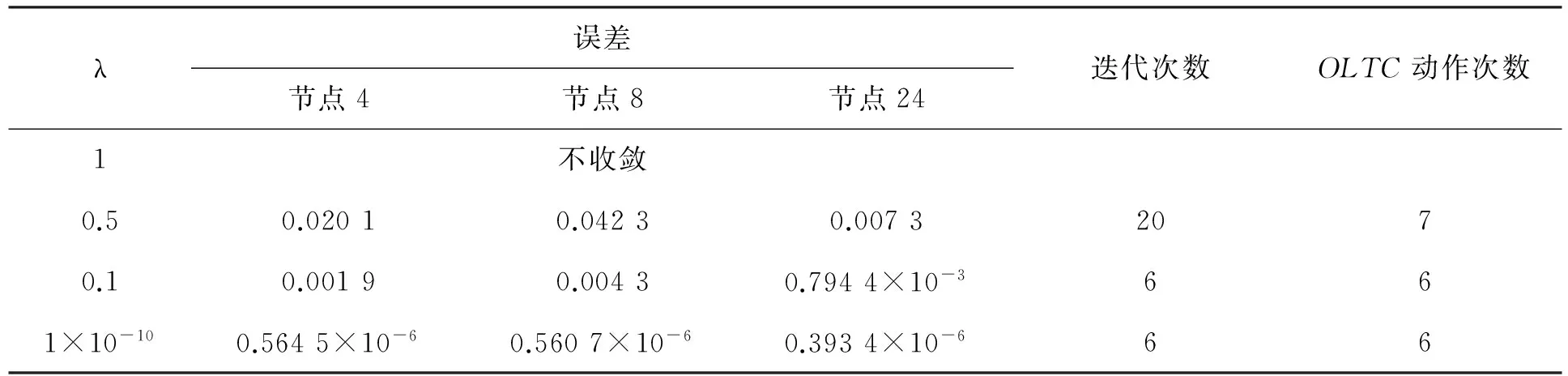
(5) 若j号OLTC变比上调Δkj,计算此时ΔVi.若ΔVi>0,j (6) 按所确定的变比调节量调节OLTC,若同一OLTC有多个调节量,按最大调节量调节. (7) 若风功率改变,更新电压对变比的灵敏度矩阵,重复步骤(1)~(6),否则调压完成. 由于式(1)忽略变比的离散约束,由此得到的灵敏度不很准确,用于指导OLTC变比调节存在误差,特别对于含有多个OLTC的系统,连续变比得到的调压结果甚至会出现错误,故需计及变比离散性. 2.1OLTC变比的0-1化 OLTC变比和其分接头所在档位的关系为 (5) 对OLTC分接头的最高档位进行二进制编码,确定与OLTC对应的0-1变量个数,利用式(5)将OLTC变比转化为这些 0-1变量的线性组合,即实现了OLTC变比0-1化.第i个OLTC变比的0-1变量表达式为 (6) 其中:Ni为第i个OLTC的0-1变量个数;Tij是第i个OLTC的第j个0-1变量.将所有OLTC变比0-1化,其0-1变量总数N=N1+N2+…+Nn. 2.2基于NCP函数的连续化变比灵敏度算法 对任意(a,b)T∈R2,若φ(a,b)=0与互补约束条件a≥0,b≥0,ab=0等价,则称φ为NCP函数.NCP函数连续化0-1变量的方法是先将0-1变量约束转换为互补约束,再经光滑化的NCP函数转化为等价的光滑方程组. 使用x∈{0,1}表示的互补约束条件为 (7) Fiseher-Bmureister函数是一种备受青睐的NCP函数[17],其含光滑参数λ的表达式为 (8) 令a=x,b=1-x,可得 (9) 根据互补函数定义,当λ趋于0时,φλ(x)=0和式(7)的互补约束条件等价.图1是λ取不同值时,φλ(x)的变化曲线.由图1看出,λ趋于0时,用φλ(x)=0等价式(7)更准确. 引入的连续变量Y=[y1T,y2T, …,ynT]T,其中yi=[yi1,yi2, …,yij,…,yiNi]T,0≤yij≤1.采用φλ(yij)=0光滑逼近Tij∈{0,1},根据上述分析,对于每一个0-1变量,yij均需引入的等式约束条件为 (10) 则OLTC变比的连续变量表达式为 (11) 鉴于NCP函数算法增加了等式约束条件,则可按下式扩展雅克比矩阵 (12) 其中:JφY为等式约束的连续变量雅克比子矩阵. 节点电压的连续变量灵敏度矩阵为 (13) 由式(11)得 (14) 记Myiki=[∂yi1/∂ki, ∂yi2/∂ki, …, ∂yiNi/∂ki]T,NCP函数算法下连续变量对OLTC变比的导数矩阵为 (15) 其中:blkdiag函数用于生成块对角矩阵.基于NCP函数的连续化变比灵敏度矩阵为 (16) 其中:Λ=diag([1/N1, 1/N2, …, 1/Nn]). 图1 不同λ值对应的φλ(x)Fig.1 φλ(x) with different λ 2.3算法参量对OLTC变比调节的影响 将摄动法求得的灵敏度作为准确值s*,算法误差e用算法所得灵敏度s与s*的相对误差绝对值来描述,即e=|(s-s*)/s*|.由图1可知,连续变量以0.5为参考点,其初值离参考点越近,λ越大,NCP函数变化越平缓,算法在迭代求解过程中,其牛顿下降方向变化越慢,致使算法迭代次数增加甚至不收敛;λ越小,0-1变量约束越准确,算法误差越小;λ足够小(可小至0)时,算法误差均很小且基本保持不变.算法不收敛,无法由算法计算电压对变比的灵敏度.算法误差越大,所得灵敏度越不准确,用于指导OLTC变比调节时越易造成控制误差. 算例采用IEEE RTS24系统,有5条变压器支路(3-24、9-11、9-12、10-11、10-12),假设全为OLTC支路.为更好验证调压效果,将有功和无功负荷增加20%.取节点8和17为风电接入点,风电装机容量为500 MW,风电机组按恒功率因数方式运行(cosφ=0.95).节点8时序的风速和风电机组出力(基准功率为100 MVA)见图2,节点17的时间顺序与节点8的相反.节点电压范围取0.95~1.05 pu;变比可调范围为0.9 ~1.1 pu,步长为0.025 pu,共9个档位.每个OLTC变比由4个0-1变量线性表示,共需引入20个连续变量,将连续变量初值与参考点的距离记为dy.普通变比灵敏度算法简称为普通算法.各OLTC当前的变比分别为1.075,0.95,1,0.9和1.025 pu.每次最大变比调节量为0.05 pu,调节时间间隔为3 h,分接头日最大允许动作次数为4. 图2 时序的风速和风电机组出力Fig.2 Chronological wind speed and wind power 3.1算法的有效性验证 由普通算法(算法迭代次数为6)得到的变比分别为1.116 1,0.987 4,1.025 5,0.924 7和1.037 8 pu.令dy=0.4,λ=1×10-10,该初始值下,该文算法的迭代次数为6,得到的变比均是变比当前值.以节点3,4,8,9和24的电压对3-24支路变比的灵敏度为例,取不同的变比摄动量Δk,得到普通算法和该文算法的误差如表1所示.由表1可以看出:普通算法得到的节点电压对变比的灵敏度误差较大.该文算法误差较小,且没有增加迭代次数;当Δk逐渐减小时,该文算法的误差亦逐渐减小,可见该文算法具有有效性.这种现象的出现源于普通算法不满足变比离散约束,而该文算法满足变比离散约束. 表1 普通算法和该文算法的误差 3.2风电系统的电压控制 该系统下,风速波动时,节点3,4,8,9和24电压容易越限.无任何调节措施的这些节点电压变化情况见图3.为抑制电压越限,分别使用该文算法和普通算法得到的灵敏度来指导OLTC变比调节,不同取整函数对应的OLTC调压效果见图4,调节过程见图5. 图3 无任何调节措施的电压变化情况Fig.3 Changes in voltage for no regulation to OLTC 图4 不同取整函数对应的OLTC调压效果Fig.4 Results of regulation to OLTC for different integral functions 图5 不同取整函数对应的OLTC调节过程Fig.5 Regulatory processes of OLTC for different integral functions 从图3知,无任何调节措施时,风速波动容易导致电压越限.某些节点的电压越限量较大,且持续时间很长(节点24),威胁电力设备甚至系统的安全运行.从图4知,电压越限量较图3有较大程度的缓解,且当取整函数为ceil函数时,由该文算法指导OLTC变比调节,基本将越限电压校正至安全范围.将图4中的a与c及图5中的a与c进行比较可知,使用普通算法指导OLTC变比调节,电压越限节点数和OLTC动作次数均比该文算法对应的值大.将图4中的b与d及图5中的b与d进行比较可知,普通算法和该文算法的OLTC动作次数虽然相等,但是在12时段,9-12支路的变比为变比上限,没有向上调节的裕度,不利于应对后续时段系统的随机性扰动;另外普通算法的调压效果较差,存在节点电压越限,且持续时间较长(从图4d知近1h).出现这些现象的原因在于:普通算法忽略变比的离散约束,算法误差较大,所得灵敏度不准确,用于指导OLTC变比调节时易造成控制误差,具体表现为OLTC动作次数增加,调压效果降低,而该文算法能有效降低控制误差. 3.3对OLTC变比调节影响因素的分析 取Δk=0.000 001pu,以节点4,8和24的电压对3-24支路变比的灵敏度为例,分析OLTC变比调节的影响因素.令λ=1×10-10,改变dy,得到dy对OLTC动作次数、该文算法的误差和迭代次数的影响(见表2).令dy=0.4,改变λ,得到λ对OLTC动作次数、该文算法的误差和迭代次数的影响(见表3).dy和λ对OLTC调压效果的影响见图6. 表2 λ= 1×10-10时,dy对OLTC动作次数、该文算法误差和迭代次数的影响 表3 dy=0.4时,λ对OLTC动作次数、该文算法误差和迭代次数的影响 图6 λ和dy对OLTC调压效果的影响Fig.6 Effect of λ and dy on the results of regulation to OLTC 从表2,3知,λ越大且 dy越小,该文算法的迭代次数越大甚至不收敛;λ很小且dy高于其下限(从表2知下限可取为0.026)时,算法误差很小,且基本保持不变;λ增加时,算法误差增大.由表2,3及图6分析可知,λ和dy对OLTC变比调节的影响为:(i) λ很小时,dy减小,电压越限的节点数和OLTC动作次数不变.(ii) dy不变时,λ增加初期,电压越限的节点数和OLTC动作次数不变,但λ继续增加时,OLTC动作次数也随之增加. 基于变比离散特点,笔者提出了NCP函数的连续化变比灵敏度算法,可得到以下结论: (1) 相比普通变比灵敏度算法,在适当参数及初值下,该文算法能满足变比的离散约束,误差较小且不增加迭代次数.风电波动致使电压越限时,该文算法可准确用于指导OLTC变比调节,有效降低了普通变比灵敏度算法的控制误差. (2) 初值离参考点越近,λ越大,该文算法的迭代次数越多甚至不收敛;λ较小时,初值与参考点距离高于初值下限时,算法误差较小. [1]王小海, 齐军, 侯佑华, 等. 内蒙古电网大规模风电并网运行分析和发展思路[J]. 电力系统自动化, 2011, 35 (22): 90-96. [2]刘雪芳. 大规模风电并网无功电压协调控制研究[D]. 济南: 山东大学电气工程学院, 2013. [3]陈惠粉, 乔颖, 闵勇, 等. 风电场动静态无功补偿协调控制策略[J]. 电网技术, 2013, 37 (1): 248-254. [4]LIS,YORINON,DINGM,etal.Sensitivityanalysistooperationmarginofzone3impedancerelayswithbuspowerandshuntsusceptance[J].IEEETransonPowerDelivery, 2008, 23 (1): 102-108. [5]肖文显, 许利军, 马孝琴. 混沌差分进化算法在复杂优化问题中的应用研究[J]. 安徽大学学报 (自然科学版), 2014, 38 (3): 32-36. [6]刘震, 陈艳浩, 肖文显. 基于模拟退火的单向环蛙跳算法在优化问题中的应用[J]. 安徽大学学报 (自然科学版), 2013, 37 (5): 25-31. [7]SOLEREM,ASADAEN,daCOSTAGRM.Penalty-basednonlinearsolverforoptimalreactivepowerdispatchwithdiscretecontrols[J].IEEETransonPowerSystems, 2013, 28 (3): 2174-2182. [8]程改红, 徐政. 电力系统故障恢复过程中的过电压控制[J]. 电网技术, 2004, 28 (11): 29-33. [9]陈曦. 基于灵敏度方法的电网安全校正策略研究[D]. 北京: 华北电力大学电气与电子工程学院, 2011. [10]张家昕, 段复建. 一种结合NCP函数的SQP滤子新算法[J]. 安徽大学学报 (自然科学版), 2010, 34 (5): 16-20. [11]WANGX,LIYZ,ZHANGSH.Oligopolisticequilibriumanalysisforelectricitymarkets:anonlinearcomplementarityapproach[J].IEEETransonPowerSystems, 2004, 19 (3): 1348-1355. [12]韦园清, 李滨, 韦化. 基于凝聚函数的电力系统无功互补优化模型与算法[J]. 电网技术, 2013, 37 (1): 156-161. [13]林济铿, 石伟钊, 武乃虎, 等. 计及离散变量基于互补约束全光滑牛顿法的无功优化[J]. 中国电机工程学报, 2012, 32 (1): 93-100. [14]卢艺. 电力系统混合整数无功优化问题的精确连续化方法研究[D]. 广州: 华南理工大学电力学院, 2010. [15]李生虎. 风力电力系统分析[M]. 北京: 科学出版社, 2012: 26-49. [16]颜伟, 田甜, 张海兵, 等. 考虑相邻时段投切次数约束的动态无功优化启发式策略[J]. 电力系统自动化, 2008, 32 (10): 71-75. [17]TORRESGL,QUINTANAVH.Optimalpowerflowbyanonlinearcomplementaritymethod[J].IEEETransonPowerSystems, 2000, 15 (3): 1028-1033. (责任编辑郑小虎) SensitivityalgorithmofOLTCforvoltagecontroltowindpowersystemsbasedontransformingtapchangestocontinuousvariables WANGYanyan1,LIShenghu1*,LEIQingkun2,DONGWangchao1 (1.SchoolofElectricalEngineeringandAutomation,HefeiUniversityofTechnology,Hefei230009,China;2.MaintenanceCompanyofStateGridAnhuiElectricPowerCorporation,Hefei230061,China) Fluctuationofwindpoweryieldsobviousandfrequentvoltagevariation.Byrelocatingvardistribution,theon-loadtapchanger(OLTC)adjustsbusvoltageswithoutadditionalinvestment.Withoutregardtothediscreteconstraintsoftapchangers,thesensitivityvaluesderivedfromcanonicalsensitivityalgorithmoftapchangersarenotverytrueandthereareerrorsforguidingregulationofOLTC.Withbinaryencoding,thetapchangersweredescribedbylinearcombinationof0-1variables,andthentransformedtocontinuousvariablesbyintroducingNCPfunction,thusasensitivityalgorithmofcontinuoustapchangersbasedontheNCPfunctionwasnewlyproposedforvoltagecontrolofwindpowersysteminthispaper.TheinfluencingfactorsonregulationofOLTCwereinvestigated.Theresultsshowedthattheproposedalgorithmwaseffectiveandfeasible. windpowerfluctuation;on-loadtapchanger(OLTC);voltagecontrol;sensitivity;discretevariable;NCPfunction 10.3969/j.issn.1000-2162.2016.02.010 2015-10-14 国家自然科学基金资助项目(51277049) 王艳艳(1990-),女,安徽亳州人,合肥工业大学硕士研究生;李生虎(通信作者),合肥工业大学教授,博士生导师,E-mail:shenghuli@hfut.edu.cn. TM734 A 1000-2162(2016)02-0054-082 基于NCP函数的连续化变比灵敏度算法
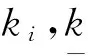


3 算例分析





4 结束语
