随机环境对n中取k系统寿命的影响

李　娉， 凌晓亮

(1.北京科技大学 东凌经济管理学院，北京100083；2. 河北科技大学 理学院，河北 石家庄 050018)



随机环境对n中取k系统寿命的影响

李娉1， 凌晓亮2

(1.北京科技大学 东凌经济管理学院，北京100083；2. 河北科技大学 理学院，河北 石家庄 050018)

在多元比例优势混合模型框架下，研究随机环境对n中取k系统寿命的影响，得到了n中取k系统寿命和环境变量之间的正似然比相依性质. 利用随机序，研究环境变量对n中取k系统寿命的影响.

比例优势模型；相依性；随机序；混合模型

在可靠性理论中，出于系统可靠性计算的易处理性考虑，大量文献常常假定构成系统的n个元件的随机寿命是相互独立的. 但在实际情形中，元件的随机寿命之间常常存在某种形式的相依性. 文献[1-2]指出共同的随机环境是导致系统元件随机寿命之间相依性存在的一个重要原因，其中随机环境被定量地描述为一个随机变量，于是系统中各个元件的联合寿命分布便可用一个多元混合模型来描述. 构成一个可靠性系统的n个元件的随机寿命用T1,…，Tn表示，其工作的共同随机环境用随机变量V来表示. 在给定V=v，T1,…，Tn是条件独立的，T1,…，Tn的联合可靠度函数可表示为

(1)

其中：GV为V的分布函数. 模型(1)被称作多元混合模型，在可靠性、风险等诸多领域有着广泛的应用[3-6].一些文献在特殊的多元混合模型框架下，研究了随机环境对n中取k系统的随机寿命的影响问题.如文献[7]假设组成系统的各个元件的联合寿命分布服从多元混合指数分布模型；文献[8]假设组成系统的各个元件联合寿命分布服从多元尺度变化混合模型，推广了文献[7]的研究结论；文献[9]假设组成系统的n个元件联合寿命分布分别服从多元比例失效率混合模型和多元比例反向失效率混合模型.

文献[10]介绍了比例优势模型，在此模型下，给定V=v时，第i个元件的条件可靠度函数为

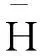
在多元比例优势混合模型框架下，论文考虑随机环境优劣对n中取k系统随机寿命的影响问题. 第一部分介绍论文要用到的一些预备知识. 第二部分建立了随机环境变量和n中取k系统随机寿命之间的相依关系.第三部分利用不同的随机序，研究了随机环境下n中取k系统随机寿命的随机比较问题.

论文中所涉及的随机变量均为非负随机变量，递增和递减分别表示非递减和非递增，所有的期望和积分均假定存在.

1　预备知识

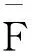
(1) 若g(x)/f(x)关于x递增，则称X以似然比序小于Y(记为X≤lrY).

(3) 若G(x)/F(x)关于x递增，则称X以反向故障率序小于Y(记为X≤rhY).

上述随机序具有以下关系

定义2[13]令 (X,Y) 是二维连续型随机变量，概率密度函数为f(x,y).

(1) 若对所有的x，有P(X>x|Y>y)关于y是递增函数，则称X关于Y是右尾递增的(righttailincreasing)，记为RTI(X|Y).

(2) 若对所有的x1≤x2和y1≤y2，有f(x1,y1)f(x2,y2)≥f(x1,y2)f(x2,y1) 成立， 则称X和Y是正似然比相依(positivelylikelihoodratiodependent)，记为PLR(X,Y).

上述相依概念具有如下关系式

PLR(X,Y)⟹RTI(X|Y).

(2)

若对所有的θ1≤θ2和x1≤x2，有ψ(θ1,x1)ψ(θ2,x2)≥ψ(θ1,x2)ψ(θ2,x1)成立，则称函数ψ(θ,x)在θ∈和x∈上是TP2.

引理 1[14]令ψ(θ,x)在θ∈和x∈上是TP2，且hi(θ)在i∈{1,2}和θ∈上是TP2(totalpositivityofordertwo)，其中hi(θ)关于θ是一概率密度函数，i=1,2. 则φi(x)=∫ψ(θ,x)hi(θ)dθ在i∈{1,2}和x∈上是TP2.

引理2[12](1)X≤hrY充要条件是E[α(X)]E[β(Y)]≤E[α(Y)]E[β(X)]成立，其中β≥0，α/β和β均为递增函数.

(2)X≤rhY充要条件是E[α(X)]E[β(Y)]≥E[α(Y)]E[β(X)]成立，其中β≥0，α/β和β均为递减函数.

2　相依性质

n中取k系统是可靠性工程或理论中较为常见的一种系统结构，此系统由n个元件构成，系统工作当且仅当至少有k个元件工作. 在多元比例优势混合模型框架下，构成系统的n个元件的随机寿命(T1,…,Tn)的联合可靠度函数表示为

因此，由此n个元件构成的n中取k系统的随机寿命便对应元件随机寿命T1,…,Tn的第n-k+1个顺序统计量. 用Tn-k+1:n(V)表示在随机环境V下n中取k系统的随机寿命，Tn-k+1:n(v)表示在随机环境V=v下n中取k系统的随机寿命，于是Tn-k+1:n(V)的可靠度函数为

(3)

研究两个变量之间的相依关系， 在可靠性、生存分析以及风险理论中有着重要的意义. 下面定理揭示了n中取k系统的随机寿命和随机环境之间是正似然比相依的.

定理1n中取k系统随机寿命Tn-k+1:n(V)和随机环境变量V是正似然比相依的.

证明注意到Tn-k+1:n(V)和V的联合密度函数为f(t,v)=fTn-k+1:n(v)(t)h(v). 要证明对所有的t1≤t2，v1≤v2，有fTn-k+1:n(v1)(t1)fTn-k+1:n(v2)(t2)≥fTn-k+1:n(v1)(t2)fTn-k+1:n(v2)(t1)成立. 等价地，只需证明对任意v1≤v2，有fTn-k+1:n(v2)(t)/fTn-k+1:n(v1)(t)关于t单调递增即可.

为此，令Ti(v)表示给定V=v条件下，第i个元件的随机寿命，i=1,…,n，当v1≤v2时，易得

易证

关于t单调递增，于是Ti(v1)≤lrTi(v2). 利用文献[12]中的定理1可得Tn-k+1:n(v1)≤lrTn-k+1:n(v2)，即fTn-k+1:n(v2)(t)/fTn-k+1:n(v1)(t) 关于t单调递增.

由式(2)，既然正似然比相依性质蕴含着右尾递增性质，下列结论由定理1得到.

结论1(1)Tn-k+1:n(V)关于V是右尾递增的. 即对所有的t和v1≤v2， 有

(2)V关于Tn-k+1:n(V)是右尾递增的. 即对所有的v和t1≤t2， 有

上述结论指出n中取k系统的运行环境越温和，则在随机序意义下系统的运行时间越长.

3　随机比较

随机环境V分布函数的选择取决于系统运行的实际条件，若环境具有变量V1的分布，而采取的是V2的分布，研究V1和V2的分布的变化对Tn-k+1:n(V1)和Tn-k+1:n(V2)分布的影响就比较重要了.下述定理给出了两个随机环境变量V1和V2之间的随机序关系是如何转化为Tn-k+1:n(V1)和Tn-k+1:n(V2)之间的随机序关系的.

定理2若V1≤hrV2，则Tn-k+1:n(V1)≤hrTn-k+1:n(V2).

证明以下公式成立

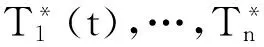
(4)

当t1≤t2时，容易验证

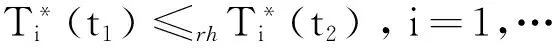
利用式(4)可得

即Tn-k+1:n(V1)≤hrTn-k+1:n(V2).

定理3若V1≤rhV2，则Tn-k+1:n(V1)≤rhTn-k+1:n(V2).

证明由定理2证明可知

并且

(5)

成立. 当t1≤t2时，可得

利用式(5)可得

故

定理4(1) 若V1≤lrV2，则Tn-k+1:n(V1)≤lrTn-k+1:n(V2);

(2) 若V1≤stV2，则Tn-k+1:n(V1)≤stTn-k+1:n(V2) .

证明(1) 由定理1的证明得Tn-k+1:n(v1)≤lrTn-k+1:n(v2)，即fTn-k+1:n(v)(t)关于(t,v)是TP2的. 注意到gi(v)关于(i,v)是TP2的，且Tn-k+1:n(V)的概率密度函数

关于(i,t)是TP2的，即

成立，即

[1]SHAKEDM.Aconceptofpositivedependenceforexchangeablerandomvariables[J].TheAnnalsofStatistics, 1977, 5(3): 505-515.

[2]LINDLEYDV,SINGPURWALLAND.Multivariatedistributionsforthelifelengthsofcomponentsofasystemsharingacommonenvironment[J].JournalofAppliedProbability, 1986, 23(2): 418-431.

[3]KHALEDIBE,KOCHARSC.Dependencepropertiesofmultivariatemixturedistributionsandtheirapplications[J].AnnalsoftheInstituteofStatisticalMathematics, 2001, 53(3): 620-630.

[4]BELZUNCEF,MERCADERJA,RUIZJM,etal.Stochasticcomparisonsofmultivariatemixturemodels[J].JournalofMultivariateAnalysis, 2009, 100(8): 1657-1669.

[5]DENUITM,FROSTIGE.Comparisonofdependenceinfactormodelswithapplicationtocreditriskportfolios[J].ProbabilityintheEngineeringandInformationalSciences, 2008, 22(1): 151-160.

[6]FROSTIGGE,DENUITTM.Dependenceinfailuretimesduetoenvironmentalfactors[J].StatisticsandProbabilityLetters, 2009, 79(4): 487-495.

[7]LEFVREC,MALICEMP.Onasystemofcomponentswithjointlifetimesdistributedasamixtureofindependentexponentiallaws[J].JournalofAppliedProbability, 1989, 26(1): 202-208.

[8]MACS.Uniformstochasticorderingonasystemofcomponentswithdependentlifetimesinducedbyacommonenvironment[J].Sankhyā:TheIndianJournalofStatistics,SeriesA, 1999, 61(2): 218-228.

[9]LINGXL,ZHAOP,LIXH.Onasystemofnonhomogeneouscomponentssharingacommonfrailty[J].JournalofStatisticalPlanningandInference, 2012, 142(6): 1330-1338.

[10]BENNETTS.Analysisofsurvivaldatabytheproportionaloddsmodel[J].StatisticsinMedicine, 1983, 2(2): 273-277.

[11]LINGXL,LIP.Stochasticcomparisonsforthenumberofworkingcomponentsofasysteminrandomenvironment[J].Metrika, 2013, 76(8): 1017-1030.

[12]SHAKEDM,SHANTHIKUMARJG.Stochasticorders[M].NewYork:Springer-Verlag, 2007.

[13]NELSENRB.Anintroductiontocopulas[M].NewYork:Springer-Verlag, 1999.

[14]KARLINS.Totalpositivity[M].Stanford:StanfordUniversityPress, 1968.

(责任编辑朱夜明)

Impactofrandomenvironmentonthelifetimeofkout ofnsystem

LIPing1,LINGXiaoliang2

(1.DonlinksSchoolofEconomicsandManagement,UniversityofScienceandTechnologyBeijing,Beijing100083,China;2.CollegeofSciences,HebeiUniversityofScienceandTechnology,Shijiazhuang050018,China)

Undertheframeworkofmultivariateproportionaloddmixturemodel,thispaperinvestigatedtheimpactofrandomenvironmentonthelifetimeofkoutofnsystem.Thepositivelikelihoodratiodependencebetweenthelifetimeofkoutofnsystemandtheenvironmentalvariablewasobtained.Usingdifferentstochasticorders,theimpactofenvironmentalvariableonthelifetimeofkoutofnsystemwasstudied.

proportionaloddmodel;dependence;stochasticorder;mixturemodel

10.3969/j.issn.1000-2162.2016.02.004

2015-01-12

国家自然科学基金资助项目(11426084,11501162);河北省自然科学基金资助项目(A2014208133)

李娉(1981-)，女，河北石家庄人，北京科技大学博士研究生; 凌晓亮(1982-)，男，河北邯郸人，河北科技大学副教授，博士.

O212.2

A

1000-2162(2016)02-0021-05