任意寿命分布单元表决系统备件需求量的解析算法

2016-09-20刘任洋李庆民海军工程大学兵器工程系湖北武汉430033

系统工程与电子技术 2016年3期

刘任洋，李庆民，王慎，李华（海军工程大学兵器工程系，湖北　武汉430033）

刘任洋，李庆民，王慎，李华
（海军工程大学兵器工程系，湖北武汉430033）

表决结构广泛存在于装备的可靠性设计中。针对表决系统备件需求计算困难、不准确的问题，提出了一种基于寿命分布等效的表决系统备件需求量计算方法。首先通过R-等效方法将系统中的非指数单元转化为指数单元；而后将多指数单元表决系统等效为伽马系统并给出等效伽马系统参数的经验计算公式；在此基础上以可用度为保障约束指标，利用伽马分布的可加性得到备件计算结果；最后在实际算例中，通过与仿真结果的比较表明，此解析算法对于指数单元具有较高精度，对于非指数单元，在可用度较高的情况下亦能满足精度要求。

表决系统；R-等效；伽马等效；备件需求量；可用度

网址：w w w.sys-ele.co m

0 引言

在装备的可靠性设计中，为了满足一定的可靠性要求，通常采用表决结构作为一种冗余设计来提高装备的整体可靠度［1-4］：即在N 个单元组成的系统中，只要有k（1≤k≤N）个单元正常工作，系统则不会失效，记为k/N（G）。备件作为装备维修保障的重要资源，影响着装备的作战能力和全寿命保障费用［5-6］。因此，精确计算备件需求量不论是对装备的保障性设计还是装备的有效运行都具有重要意义。

国内外已有很多学者对表决系统的备件需求和配置问题开展研究。文献［7］分析了k/N冷备份冗余系统的建模方法，给出了精确和近似两种计算单层级k/N系统可用度的方法；文献［8］从单部件可用度入手，分析和推导了冷备份系统可用度的计算方法；文献［9］研究了备件保障与装备战备完好性的关系，建立了k/N系统的备件配置优化模型；文献［10］针对已有研究未考虑备件报废的问题，将报废率引入k/N系统的备件配置模型中；国军标《备件供应规划要求》中将多指数k/N 系统假设为串联结构，即只要有一个单元失效则立即开展换件维修工作，从而利用“指数寿命件备件需求模型”能很方便的得到备件结果。

尽管以上对表决系统备件需求的研究取得一定的成果，但在实际应用中还存在以下不足：首先，现有研究几乎都是假设系统中单元寿命服从指数分布，而对非指数分布的情况讨论较少；其次，对于故障单元的更换方式，大部分文献均采用“坏一件换一件”的模式［11-13］，但在某些场合，如执行任务的舰艇编队，由于时间紧急，对故障件进行频繁的更换和维修往往影响任务的执行，此时，采用批量更换策略却能起到更好的效果；第三，国军标将表决系统假设为串联系统的方法虽然易于计算，但得到的备件需求结果是保守、不准确的。

针对上述问题，本文提出一种表决系统备件量的解析算法。依次通过R-等效和伽马等效过程将任意寿命分布单元表决系统等效为伽马系统；根据伽马分布的可加性，以部队常用的可用度为保障约束指标，对系统备件量进行迭代求解。

1 基于R-等效的任意分布单元指数近似方法

1.1 R-等效原理

由于指数分布失效率为常数，能大大简化备件计算过程，因此在处理非指数单元时若能将其等效为指数单元就可为备件需求计算带来方便。文献［14］提出了基于累计失效次数相等的指数近似方法，该方法精度较高且易于实现，本文在其基础上根据失效次数与可用度之间的关系，引入R-等效（可靠度相等）原则将表决系统中的非指数单元转化为指数单元。

可靠度函数R（t）的定义为系统在指定条件下和指定的时间t内不发生故障的概率。指数型单元的可靠度函数为

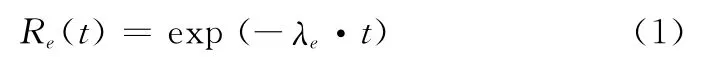
R-等效原理就是从表征单元寿命的基本参数出发，采用可靠度相等的原则，将非指数单元等效为指数单元。设任务时间为T，则有

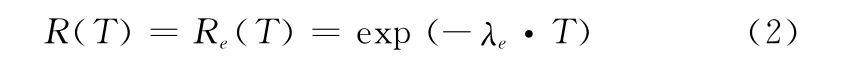
式中，λe为等效指数单元的失效率，得到

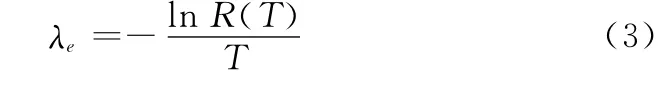
一般来说，故障时刻在平均寿命E处的概率较大。通过大量试验表明，当任务时间超过平均寿命时仍用平均寿命代入计算具有更高的精度：

R（T）的物理意义为单元能够正常工作至时间T的概率，若按一定的统计方法对失效次数进行统计，就能对其进行估计。以下给出几种典型寿命分布单元的R-等效计算方法。

1.2 威布尔型单元等效方法

对于服从尺度参数为α，形状参数为β的威布尔单元W（α，β），其可靠度函数［15］为

平均寿命为

1.3 正态型单元等效方法

对于服从均值为μ，标准差为σ的正态单元N（μ，σ），其可靠度函数为

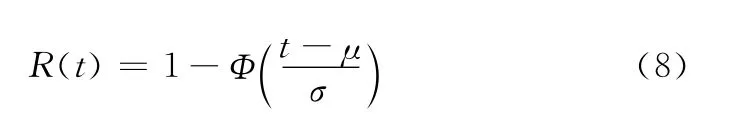
平均寿命为μ。根据R-等效原则，在任务时间T内，得到等效指数单元失效率

1.4 伽马型单元等效方法

对于服从形状参数为a，尺度参数为b的伽马单元G（a，b），其可靠度函数为

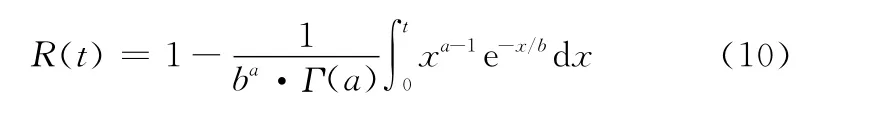
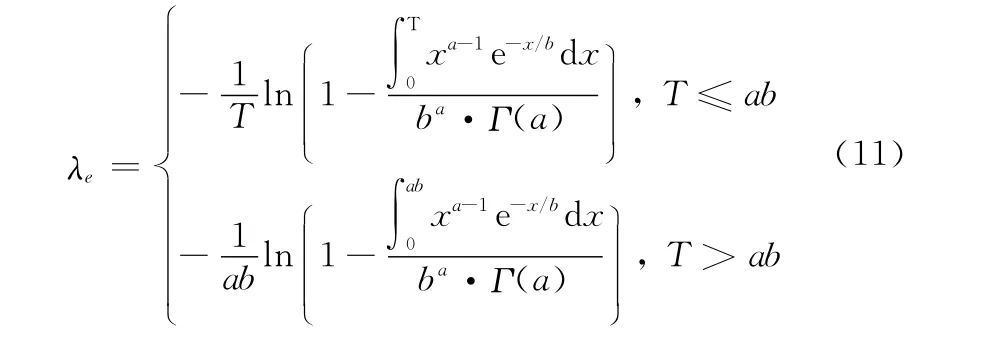
2 基于伽马等效的表决系统备件量确定

2.1 伽马等效原理

在可靠性理论中，指数分布是a=1的伽马分布，伽马分布是指数分布的推广。由伽马分布性质可知，N个伽马分布之和仍为伽马分布。针对表决系统寿命分布难确定的问题，如果能将其等效为伽马分布，则利用伽马分布的可加性能很好模拟系统的换件过程从而快速方便的计算备件需求量。

依据冲击失效理论：寿命服从伽马分布的系统G（a，b），可经受若干次外界冲击，而当冲击次数累积达到a次时系统就会失效。根据k/N表决系统定义：当失效单元数量累积到（N-k+1）时，该系统会失效。因此，G（a，b）系统和k/ N表决系统二者在失效条件上的物理意义是等效的。

通过上述分析，本文在R-等效的基础上将多指数单元表决系统近似等效为寿命服从伽马分布的伽马系统G（a，b）。如果表决系统有足够的寿命样本，参数a、b可通过样本拟合的方式得到，但实际保障过程中可得的装备故障数据往往很少，这将严重影响拟合效果造成参数估计不准确。

本文给出一种求解参数a、b的经验公式。k/N系统可靠度函数为

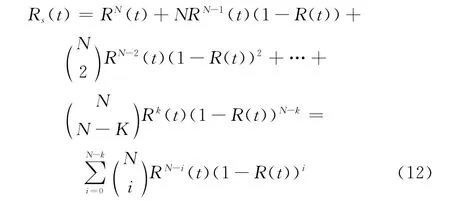
式中，Rs（t）为系统可靠度；R（t）为单元可靠度。对于服从任意寿命分布的单元，经R-等效后均可近似看作失效率为λe的指数分布，则有

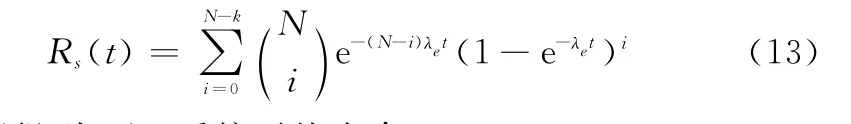
进而得到k/N系统平均寿命

将k/N系统等效为伽马系统G（a，b）后，由伽马分布性质可知Es=ab，因此，令a=N-k+1，则b此经验公式操作简单，不需要获取系统的寿命样本，可为工程应用带来便利。

2.2 表决系统备件量确定流程

在换件维修模式下，寿命服从参数（a，b）的伽马系统，假设备件更换时间忽略不计，则系统在n次换件下的寿命仍服从伽马分布，其参数为（a（n+1），b）。本文选取可用度作为系统的保障指标，其计算公式为

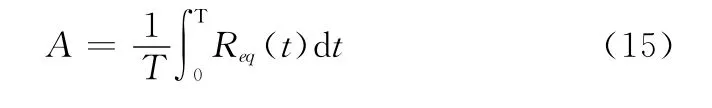
Req（t）为考虑换件次数下等效伽马系统G（a（n+1），b）的可靠度函数

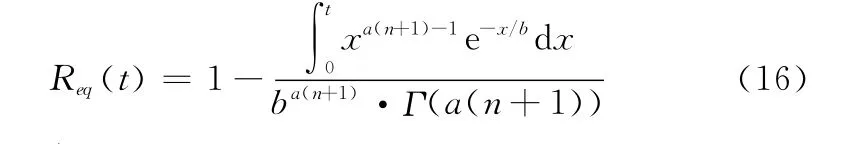
式（16）建立了可用度与换件次数之间的关系，因此在给定的可用度指标下即可利用该式不断迭代计算换件次数和备件量。下面给出由任意分布单元构成的表决系统备件量计算流程，如图1所示。

图1 任意分布单元表决系统备件需求量计算流程

步骤1 根据R-等效原则，利用式（4）将k/N系统中的非指数单元等效为指数单元。

步骤2 将等效后的多指数单元系统等效为伽马系统G（a，b）。参数a，b的经验计算公式如下：

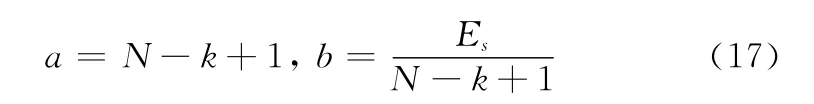
步骤3 设置保障指标目标值A0，令换件次数n=0。

步骤4 通过式（15）计算保障系统指标A。

步骤5 若A≥A0，则得到单元备件需求量S=n× （N-k+1），否则置n=n+1，转入步骤4。

3 算例分析

某8/10系统由10个蓄电池单元组成，当有效单元数量少于8个时，该系统发生故障，对失效单元进行换件维修。系统可用度目标值A0设为0.98，任务时间T为1 500 h。为了更充分的说明本文方法的正确性和有效性，以下分别以单元寿命服从指数分布、威布尔分布、正态分布以及伽马分布为例进行计算和讨论。

（1）当单元寿命服从λ=1/1 000的指数分布时，本文和仿真方法所得备件需求量都为15，算法的迭代过程如表1所示。图2为该指数单元在不同任务时间下的备件量计算结果。

表1 指数单元（λ=1/1 000）备件量计算过程

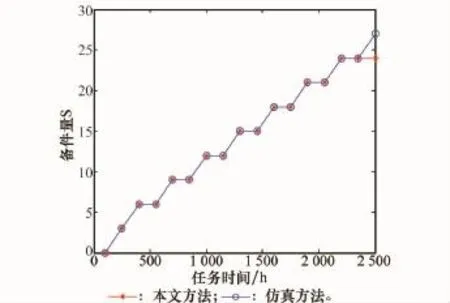
图2 本文方法和仿真方法的备件需求量对比

（2）当单元寿命服从（α，β）=（800，2）的威布尔分布时，本文和仿真方法所得备件需求量都为18，算法迭代过程如表2所示。图3为该威布尔单元在不同任务时间下的备件量计算结果。

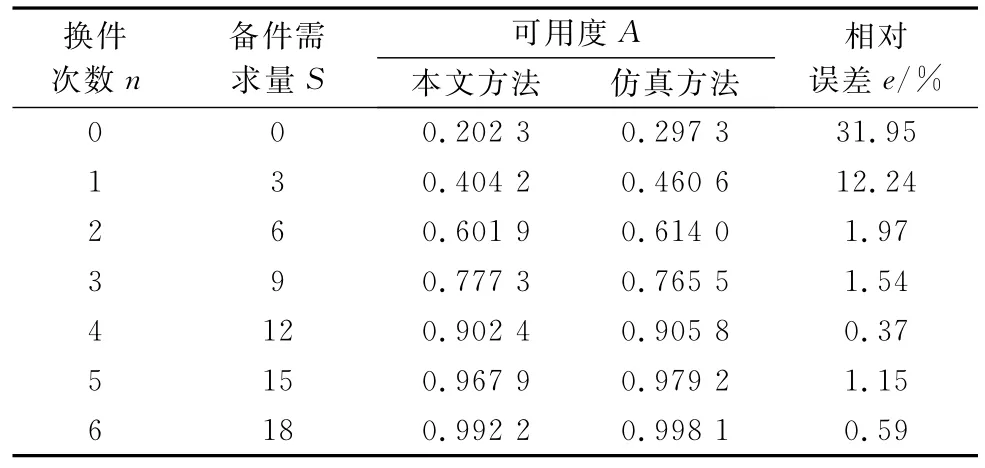
表2 威布尔单元（（α，β）=（800，2））备件量计算过程

图3 本文方法和仿真方法的备件需求量对比

（3）当单元寿命服从（μ，σ）=（1 000，500）的正态分布时，本文和仿真方法所得备件需求量都为12，算法迭代过程如表3所示。图4为该正态单元在不同任务时间下的备件量计算结果。

表3 正态单元（（μ，σ）=（1 000，500））备件量计算过程

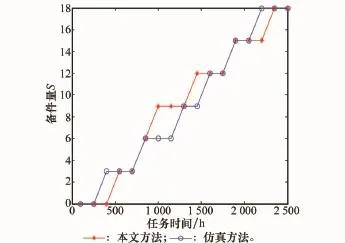
图4 本文方法和仿真方法的备件需求量对比

（4）当单元寿命服从（a，b）=（1 000，500）的伽马分布时，本文和仿真方法所得备件需求量都为21，算法迭代过程如表4所示。图5为该伽马单元在不同任务时间下的备件量计算结果。

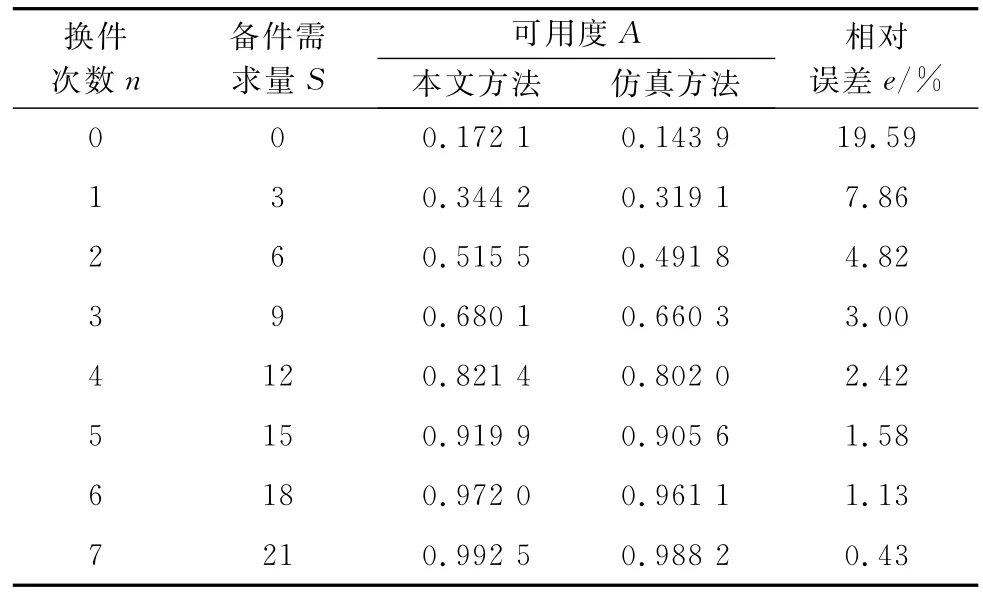
表4 伽马单元（（a，b）=（0.8，1 000））备件量计算过程

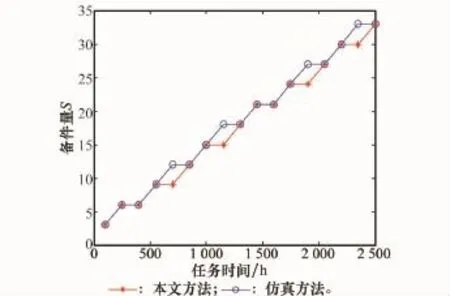
图5 本文方法和仿真方法的备件需求量对比

综合以上算例可以看出，本文算法应用于指数单元时相对误差最小，在0.05%～1.17%之间，这是因为本文描述的两次等效过程都为近似等效过程，存在一定的误差积累，而指数单元只需对其进行一次伽马等效，这也说明了本文的伽马等效方法具有较高的精度。对于其他分布类型的单元，在可用度较低时相对误差普遍较大，如威布尔单元在备件量为0时，可用度的相对误差达到了31.95%，但随着可用度的逐渐增大，相对误差逐步减小至0.95%。事实上，虽然在低可用度下误差较大，但本文提出的等效算法仍有其适用性：首先，低可用度下的备件配置结果或可用度评估往往不是装备保障人员所关心的，因为通常情况下，为了保证装备的战备完好性和执行任务的能力，一般要求可用度在0.8甚至0.95以上，而在这个范围内，以上算例中误差最大值仅为伽马单元的2.42%，完全满足一般的精度要求；其次，本文解析算法的耗时仅为仿真方法的十分之一，在面对大批量备件需求计算问题时具有明显优势。

另外还需说明的是，虽然解析方法的备件量计算结果与仿真方法有时存在较大差别，但这主要是批量换件导致的，实际的换件次数误差最多为1次。

4 结束语

本文提出了基于R-等效、伽马等效的表决系统备件量计算模型，能对任意寿命分布单元构成的表决系统备件量进行求解。算例中通过与仿真结果的比较表明，本文等效方法对指数单元具有较高精度，对于其他分布单元，在部队较为关心的高保障指标范围内，其精度也能满足要求。

［1］Krishnan R，Somasundaram S.Reliability analysis of repairable consecutivek-out-of-n：G systems with sensors and repairmen［J］.International Journal of Quality&Reliability Management，2011，28 （8）：894-908.

［2］Fang Y F，Chen J J，Cao H J.Analysis of dynamic reliability of the repairablek-out-of-nsystem under several times random shocks［J］.Journal of Xidian University，2014，41（5）：180-184.（方永锋，陈建军，曹鸿钧.可修复的k/n表决系统的可靠性分析［J］.西安电子科技大学学报，2014，41（5）：180-184.）

［3］W u W Q，Tang Y H，Y u M M，et al.Reliability analysis of akout-of-n：G repairable system with single vacation［J］.Applied Mathematical Modeling ，2014，38（24）：6075-6097.

［4］S midt-Desto m bes K S D，Heijden M C V D，Harten A V.A vailability ofk-out-of-nsystems under block replacement sharing limited spares and repair capacity［J］.International Journal of Production Economics，2007，107（2）：404-421.

［5］Francesco C，Giulio D G，M assim o T.M ulti-echelon，m ulti-indenture spare partsinventory control subject to system availability and budget constraints［J］.Reliability Engineering and System Safety，2013，119（1）：95-101.

［6］Luo Y，Ruan M Z，Li QM.Configuration project optimization for repairable spare parts under discretional structures［J］.Systems Engineering and Electronics，2012，34（9）：1865-1871.（罗，阮智，李庆民.任意结构下可修复备件的配置方案优化［J］.系统工程与电子技术，2012，34（9）：1865-1871.）

［7］Wang N C，M a L，Guo L H，et al.Availability for repairable redundancy system with the restriction of spare parts［C］∥Proc.of the18th International Conference on Industrial Engineering and Engineering Management，2011：1096-1098.

［8］de Smidt-Destombes K S，Van E N P，Barros A L，et al.A spare parts model with cold-standby redundancy on system level［J］.Computer and Operations Research，2011，38（7）：985-991.

［9］Nie T，Sheng W.Research on two-echelon supply support optimizing for repairable spare parts ofK：Nsystem［J］.Systems Engineering and Electronics，2010，34（7）：1452-1455.（聂涛，盛文.K：N系统可修复备件两级供应保障优化研究［J］.系统工程与电子技术，2010，34（7）：1452-1455.）

［10］Xue T，Feng YW，Qin Q.Optimization of repairable spare parts for K/Ncold-standby redundant system considering scraps［J］.Journal of South China University of Technology （National Science Edition），2014，42（1）：41-46.（薛陶，冯蕴雯，秦强.考虑报废的K/N冷备份冗余系统可修复备件优化［J］.华南理工大学学报（自然科学报），2014，42（1）：41-46.）

［11］Ruiz-Castro J E，Li Q L.Algorithm for a general discretekout-of-n：G system subject to several types of failure with an indefinite number of repairpersons［J］.European Journal of Operational Research，2011，211（1）：97-111.

［12］Zhang Y L，W u S M.Reliability analysis for ak/n（F）system with repairable repair-equipment［J］.Applied Mathematical Modelling，2009，33（7）：3052-3067.

［13］Chakravarthy S R，Go mez-Corral A.The influence of delivery times on repairablek-out-of-nsystem with spares［J］.A pplied Mathem atical Modelling，2009，33（5）：2368-2387.

［14］Liu T H，Zhang Z H，Liang S J，et al.Analytical algorith m of spare demand for Weibull-type repairable system［J］.Systems Engineering and Electronics，2012，34（5）：966-972.（刘天华，张志华，梁胜杰，等.威布尔型可修备件需求量的解析算法研究［J］.系统工程与电子技术，2012，34（5）：966-972.）

［15］Gan M Z，Kang J S，Gao Q.Military equipment maintenance engineering［M］.2nd ed.Beijing：National Defense Industry Press，2010.（甘茂治，康建设，高崎.军用装备维修工程学［M］. 2版.北京：国防工业出版社，2010.）

Analytical algorithm of spare demand for voting system of any life distribution units

LIU Ren-yang，LI Qing-min，W A N G Shen，LI Hua
（Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，China）

The voting structure is widely used in reliability design of equipment.For the co m putation of spare demand for the voting system is difficult and inaccurate，a method to calculate spare demand for the voting system is proposed based on life distribution equivalence.First，non exponential units are converted to exponential units by R-equivalence.Then the voting system of exponential units is converted to Gam ma system and the parameter calculation formulas for the equivalent system are presented.With constrains of availability index，the spare demand results are obtained based on the additive property of Gamma distribution.Finally，in the actual example compared with simulation results，the analytical algorith m put forward in this paper owns high precision for exponential units and can also meet precision demands under high availability for non exponential ones.

voting system；R-equivalence；Gamma equivalence；spare demand；availability

E 911；TJ 761.1

10.3969/j.issn.1001-506 X.2016.03.36

1001-506 X（2016）03-0714-05

2015-02--02；

2015-09-05；网络优先出版日期：2015-12-14。

网络优先出版地址：http：∥w w w.cnki.net/kcms/detail/11.2422.T N.20151214.1348.006.html

总装预研基金（51304302，51304303）资助课题

刘任洋（1989-），男，博士研究生，主要研究方向为装备综合保障。

E-mail：463572090@qq.com

李庆民（1957-），男，教授，博士，主要研究方向为武器系统对抗仿真、装备保障模拟与仿真。

E-mail：licheng0001@hotmail.com