基于O FD M的水声通信非一致多普勒补偿方法

2016-09-20丁鹭飞支志福戴跃伟江苏科技大学电子信息学院江苏镇江22003水声对抗技术重点实验室北京00094

系统工程与电子技术 2016年3期

王彪，丁鹭飞，支志福，戴跃伟（.江苏科技大学电子信息学院，江苏　镇江22003；2.水声对抗技术重点实验室，北京00094）

王彪1，2，丁鹭飞1，支志福1，戴跃伟1
（1.江苏科技大学电子信息学院，江苏镇江212003；2.水声对抗技术重点实验室，北京100094）

当多径信道各径多普勒因子不一致时，传统的多普勒补偿技术会带来较大的残余误差。针对此问题，通过理论推导提出了一种针对水声多径信道存在非一致多普勒扩展的补偿方法。该方法采用多次内插与快速傅里叶变换相结合的算法，首先通过对接收信号进行单次重采样预处理以降低多普勒因子大小，再利用等效信道参数估计模型，获得信道统计量后进行正交频分复用解调，实现非一致多普勒补偿。仿真结果表明，所提方法在信道信息已知与未知的条件下，都具有较高的补偿性能，特别是在非一致多普勒扩展比较严重的情况下，其优势更加明显。

水声通信；多普勒补偿；正交频分复用；时变信道

网址：www.sys-ele.com

0 引言

水声通信是在水下环境进行无线信息传输的主要工具［1］，在海洋环境数据收集、海洋探险以及潜艇通信等方面有着广泛的应用，国内外有关学者对此作了大量研究［2-4］。为了进一步提高通信速率，多载波水声通信越来越成为人们的研究重点［5］。作为多载波调制的主要方式，正交频分复用（orthogonal frequency division m ultiplexing，OFDM）技术［6］具有频谱利用率高、抗多径能力强和均衡复杂性低等优点，特别适用于带宽受限的水声通信。但是，水声信道的时变性给OFDM技术在水声通信中的直接应用带来很大挑战［7-8］。时变性的主要原因在于收发节点之间存在相对运动，导致信道的多普勒扩展，进而引起OFDM各个子载波经历不同频率偏移，产生子载波间干扰［9］（intercarrier interference，ICI），破坏了子载波之间的正交性，导致接收端解调性能恶化。

针对这种情况，有关学者对水声通信中接收信号的多普勒补偿与均衡方法进行了大量研究［10-14］。比较典型的文献中，文献［10］提出了基于重采样的线性内插多普勒补偿方法，而文献［14］更进一步地提出了基于重采样与载波频率偏移补偿相结合的针对OFDM的多普勒补偿方法。当多径信道各径的多普勒因子相等或近似相等时，这些方法能取得不错的效果，但是当各径多普勒因子存在差异，即非一致多普勒扩展存在时，这些方法往往效果不佳或失效。

非一致多普勒扩展比较吻合水声信道的实际情况［15］，目前已有少数文献开始关注这个问题。文献［15-16］提出，在非一致多普勒扩展情况下，可通过计算最优重采样因子进行单次重采样来实现多普勒补偿，并给出了几种计算最优重采样因子的准则。然而，尽管通过计算最优重采样因子可以提高接收机的补偿性能，但是当各径多普勒因子差异较大时，重采样后的OFDM信号仍会存在较大的残余多普勒扩展［17-18］，最优重采样法的补偿性能提升有限。最近，文献［17］提出了一种新颖的多次重采样接收机设计，通过使用不同的多普勒因子对接收信号进行重采样，大大提高了非一致多普勒的处理性能。然而由于其接收机是在各径多普勒因子远远小于1的假设条件下得到的，当非一致多普勒扩展比较严重时，该接收机的补偿性能会有一定程度的降低，而且该方法对多普勒估计误差也比较敏感。因此针对此问题，本文提出一种基于多次内插与一次快速傅里叶变换（fast Fourier transform，FF T）相结合的接收机设计方法，该方法能够有效地处理水声OFDM中的非一致多普勒扩展问题。计算机仿真实验表明，相对于其他方法，所提方法在信道参数信息已知与未知的情况下都具有较高的补偿性能，并且在非一致多普勒扩展非常严重的情况下，补偿性能的提升更加明显。

1 水声O FD M通信系统模型

1.1 OFD M原理

本文考虑基于循环前缀（cyclic prefix，CP）的OFDM通信系统，设T和TCP分别表示OFDM的符号周期、CP长度，则对应的子载波间隔为1/T，第k个子载波频率为

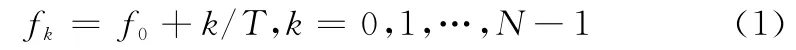
式中，f0为最低子载波频率；N为子载波个数。令d［k］表示调制到第k个子载波上的数据符号，则调制后的复OFDM带通信号为

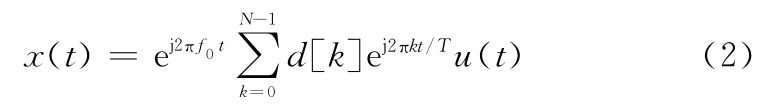
式中，u（t）=1（-Tcp≤t≤T），用来限定一个OFDM符号持续时间。

1.2 水声信道模型

移动水声信道本质上是具有时延与多普勒的双扩展信道，采用基于水声信道的射线理论模型，时变多径水声信道的冲激响应［8，14］通常表示为

式中，P为多径数目；Ap（t），τp（t）分别表示第p条路径的时变幅度衰减与时延，它们都体现出信道的时变特性。在一帧OFDM数据持续时间内，可作如下合理简化［8］：

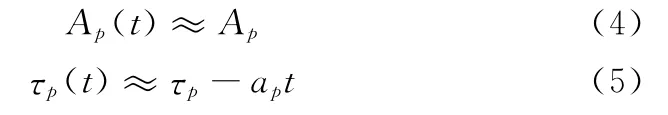
式中，ap=vp/c表示第p条路径的多普勒因子，且vp表示从第p条路径来看收发机之间的相对运动速度；c表示声波在水中的传播速度（通常约为1 500 m/s）。将式（4）和式（5）代入式（3），得到时变水声信道冲激响应为

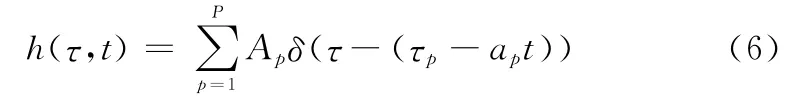
将式（2）所示OFDM带通信号与式（6）所示信道冲激响应作线性卷积，得接收端接收到的OFDM带通信号为

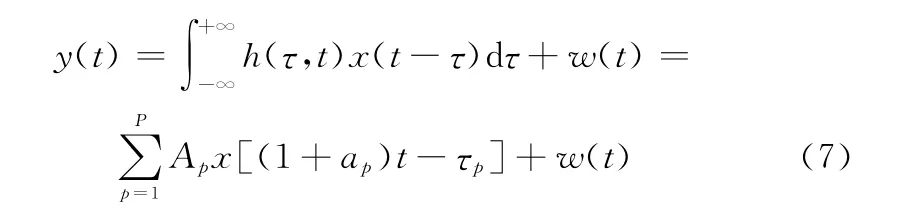
式中，w（t）表示加性高斯白噪声信号。

2 非一致多普勒补偿原理

2.1 信号帧结构与平均多普勒因子估计

本文所述非一致多普勒补偿接收机基于如图1所示的OFDM信号帧格式，由前后同步码中两个完全相同的线性调频（linear frequency modulation，LF M）信号和OFDM信号（包括CP和OFDM数据）部分组成。其中OFDM信号的数据部分携带要传输的信息符号，LF M则用来实现有关的信道参数估计（包括第2.1节的平均多普勒因子估计与第2.5节中的等效信道参数估计）。

图1 OFDM信号帧格式

2.2 单次重采样预处理

为增强多普勒补偿性能，接收机首先使用式（8）估得的平均多普勒因子对式（7）所示接收信号进行单次重采样，即

式中，w′（t）仍然为加性高斯白噪声，定义重采样后的残余多普勒因子

对比式（7）与式（9）可以发现，单次重采样之后的信号波形等价于原发射信号（见式（2））通过一个与之对应的等效信道，该等效信道冲激响应中的幅度衰减Ap和时延τp与原信道相同，但多普勒因子却变为比ap小得多的bp，在一定程度上减小了多普勒频偏的影响，方便后续处理及信道参数估计。本文称单次重采样之后的信号（式（9））为等效接收信号。

将式（2）代入式（9），得等效接收信号的表达式

式中，仍然是带通信号，令αp=Ape-j2πf0τp，两边同乘以e-j2πf0t进行下变频，得等效接收信号对应的基带信号

式中，n（t）为基带版本的复加性高斯白噪声，设其功率谱密度为N0，为进一步简化表达，令式（12）中

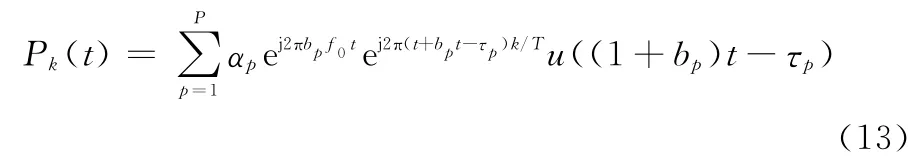
于是，等效接收信号的基带信号为

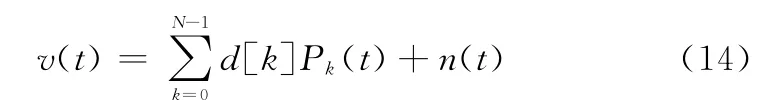
2.3 接收机数据检测

为从式（14）所示接收信号中恢复出发送的数据符号，构造如下包含数据信息的充分统计量［19］：

将式（14）代入式（15），可得

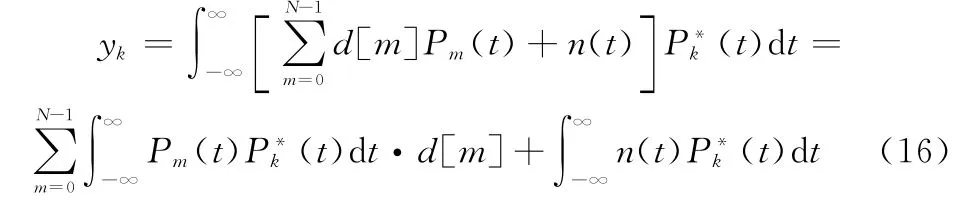
同时令

此时，式（16）进一步化为

将式（19）改写为向量形式，令y=［y0，y1，…，yN-1］T表示N个充分统计量，d=［d0，d1，…，dN-1］T表示N个数据符号，n=［n0，n1，…，nN-1］T表示由式（18）定义的噪声向量，则式（19）所示N个充分统计量对应的向量方程为

式中，Φ为信道矩阵，其元素由式（17）所定义，形式如下：

另外，值得说明的是，对于不同的k，式（18）所示噪声样值之间是相关的，这一点可由其互相关函数来说明

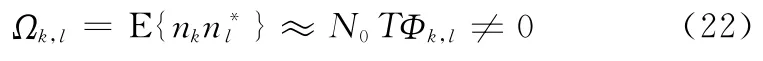
根据式（20），在接收端y可由式（14）通过一组匹配滤波器获得，信道矩阵Φ可由信道参数信息Ap，bp，τp生成，且噪声向量n各元素之间的相关函数符合式（22），则可通过线性最小均方误差（minimum mean square error，M M SE）准则由式（23）恢复出数据信息

式中，Dec（·）表示符号判决；（·）H表示矩阵的共轭转置；Ω为噪声互相关矩阵，其各元素由式（22）决定。

2.4 多次内插处理与FFT实现

前已述及，式（20）中的y可由一组匹配滤波器计算得到，但是匹配滤波器的个数取决OFDM通信系统所用的子载波数N，实际的OFDM通信系统中子载波数目通常很大（如N=512，1 024），通过式（15）来计算yk，需要大量的匹配滤波器，代价太大，实际中往往不可接受。为降低由直接匹配滤波计算充分统计量的复杂性，本文在文献［17］的基础上提出如下的基于多次内插和一次FF T相结合的yk高效计算方法，注意下文在推导中并没有假设文献［17］中的ap1这一条件，因此具有更精确的计算结果。

为得到yk的高效计算方法，将式（13）代入式（15），并考虑一个O FD M符号区间，同时作变量代换t′=（1+bp）t-τp，代入式中，则dt=dt′/（1+b），化简整理如下：

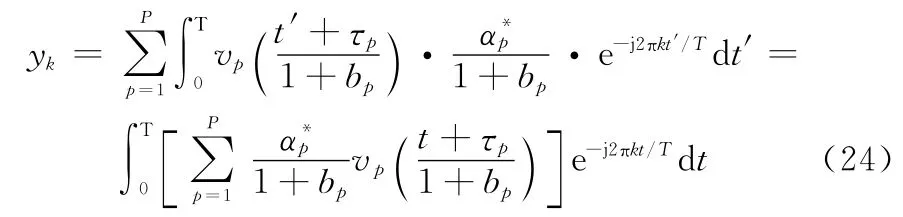
令式（24）中

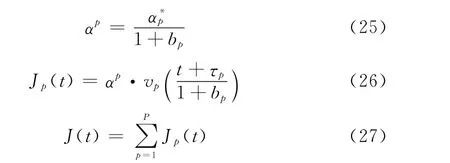
值得说明的是，在接收机处理中式（26）的vp（（t+τp）/ （1+bp））可由式（24）中vp（t）进行内插计算得到，并且根据式（27），共需进行P次内插得到J（t）。由式（25）～式（27），式（24）可化为如下形式：

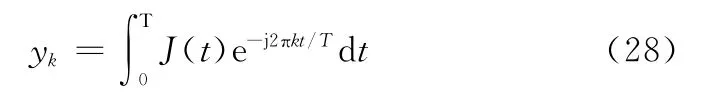
考虑到实际的接收机一般都是采用数字信号处理技术，对式（28）作离散化计算，令采样时刻t=Tn/N（n=0，1，…，N-1），式（28）化为

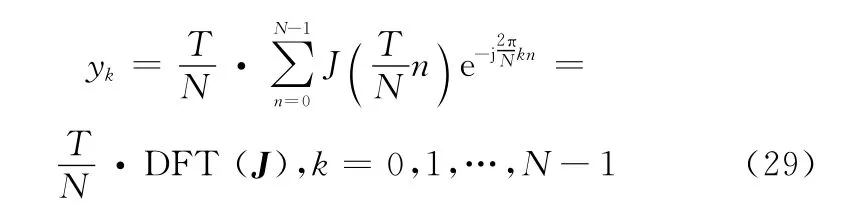
式中，D F T（·）表示信号的离散傅里叶变换；J表示J（t）的离散化形式，即

由式（29）可以看出，充分统计量yk的计算可以转化成一个离散傅里叶变换与信号抽样间隔的乘积，而离散傅里叶变换又可通过其快速算法FF T进行高效计算，相对于N次直接匹配滤波计算大大提高了计算效率。

2.5 等效信道参数估计

到目前为止，本文在式（9）中等效信道参数Ap，τp，bp完全已知的假设下详细推导了非一致多普勒补偿的基本原理，而在实际的通信系统中这些等效信道参数信息都需要由接收机估计得到，参数估计（尤其是非一致多普勒因子估计）的精确性会直接影响到接收机的处理性能。根据非一致多普勒补偿接收机的特点，本文采用文献［20］中介绍的两步稀疏信道参数估计方法，相对于传统的稀疏参数估计法，该方法将时延与多普勒因子的估计分开进行，具有实现复杂性低、估计精度高、通信开销小等优点，特别适合于本文的非一致多普勒补偿处理，其具体原理及估计过程可参考文献［20］，这里不再赘述。

3 接收机设计与步骤

根据第2节的非一致多普勒补偿原理的推导，图2给出了相应的接收机设计结构图。由图2可以看出，该接收机主要由4部分组成：A部分，完成接收信号的平均多普勒因子估计及单次重采样预处理；B部分，对单次重采样之后的接收信号进行等效参数估计；C部分，是接收机的最关键部分，对下变频及低通滤波后的基带信号进行多次内插计算及FFT处理，完成充分统计量的高效计算；D部分，利用C部分计算出的充分统计量实现OFD M的正确解调，恢复出数据信息。

图2 非一致多普勒补偿接收机结构图

根据图2所示接收机结构图，结合非一致多普勒补偿的基本原理，接收机的具体实现步骤总结如下。

步骤1 对接收信号进行帧同步，提取前后同步码信号；

步骤2 由前后LF M信号，通过相关多普勒估计法得到该帧信号的平均多普勒因子；

步骤3 由平均多普勒因子＾a对原接收信号作单次重采样预处理，获取对应的等效接收信号z（t）；

步骤4 利用单次重采样后LF M信号对z（t）进行等效信道参数估计，获得等效信道参数；

步骤5 由等效信道参数计算信道矩阵Φ和噪声互相关矩阵Ω；

步骤6 提取z（t）中的数据OFDM符号，下变频到基带并进行低通滤波；

步骤7 对第6步得到的基带信号进行多次复域内插计算并FF T处理，得充分统计量y；

步骤8 在充分统计量基础上进行OFDM解调，得解调后的数据符号。

以上处理步骤可分为两个不同阶段：第1阶段为步骤1～步骤5，其处理都是针对前后同步码信号，主要完成有关的参数估计工作，包括平均多普勒因子及等效信道参数；第2阶段为步骤6～步骤8，其处理都是针对OFDM数据符号，完成充分统计量的计算及OFDM解调。

4 仿真与性能分析

下面通过计算机仿真来验证本文所提方法的可行性与有效性。仿真所用OFDM通信系统采用BPS K调制方式，子载波数目N=512，最低子载波频率f0=21 k Hz，所用带宽B=4 k Hz，对应的子载波间隔Δf=7.81 Hz，符号持续时间T=128 ms。另外，为了简化研究过程，本文仿真过程采用非编码方式，即未采用任何的差错控制编码，接收机中的内插处理采用线性内插方式。

为使仿真分析更加全面，根据水声信道的实际情况［1718］，实验中假设两种不同的水声信道，分别命名为信道1与信道2，其详细信道参数设置如表1与表2所示。由表中数据可知，信道1是一条非常严重的5径非一致多普勒扩展信道，而信道2的多普勒扩展则相对较小。另外，仿真过程采用蒙特卡罗仿真方法，通过计算OFDM解调的误比特率（bit error rate，BE R）随信噪比（signal to noise ratio，S N R）的变化来评估各多普勒补偿方法的补偿性能。

表1 信道1参数设置

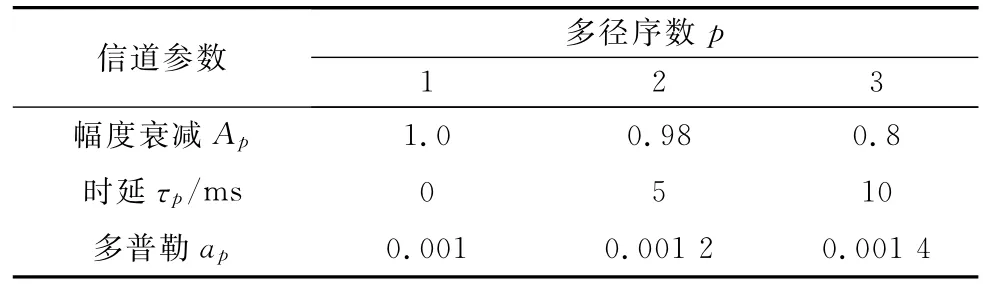
表2 信道2参数设置

4.1 信道信息完全已知时，各方法补偿性能比较

本组仿真比较了以下几种多普勒补偿方法的补偿性能，即文献［10］中的块多普勒补偿法、文献［15］中的最优单次重采样法、文献［17］中的多次重采样法以及本文方法。仿真结果如图3所示，其中图3（a）的结果对应信道1的参数设置，图3（b）对应于信道2参数设置。由图3可以看出，两种信道设置下块多普勒补偿法的补偿性能最差，误码率高达0.5左右，几乎不能正确解调，这是因为该方法只适用于一致多普勒的情况，对于非一致多普勒不再适用。

图3 信道参数已知时补偿性能

从图中最优单次重采样法的性能曲线也可以看出，尽管通过优化重采样因子可在一定程度上降低BE R，但这种降低是有限的，BE R的收敛值明显高于多次重采样法与本文方法。另外，比较多次重采样法与本文方法，它们都取得了较好的补偿效果，对于信道2小多普勒扩展的情况，它们的补偿性能比较接近；但是对于信道1这种大多普勒扩展情况，本文所提改进方法要优于多次重采样法，性能提升大约8.58%。

4.2 各补偿方法对非一致多普勒估计误差的敏感性

实际的水声通信系统中，信道参数都需要由接收机估计得到，其中非一致多普勒因子的估计结果对接收机的补偿结果影响最大，因此本组仿真假定信道参数中Ap，τp已知，考察指定多普勒估计错误对接收机补偿性能的影响。鉴于块多普勒估计法不再适用于非一致多普勒补偿，仿真中着重考虑多次重采样法、最优单次重采样法与本文方法的补偿性能。真实信道参数仍如表1与表2所示，并假定信道1的多普勒估计结果依次为0.001 1、0.002、0.003 1、0.005、0.008，即第1条与第3条的多普勒因子估计出现错误；信道2的多普勒估计结果为0.001、0.001 1、0.001 4，即第2条路径的多普勒估计存在误差。

本组仿真结果如图4所示，由图中结果可以看出，相对于第一组仿真中信道信息完全已知的情况，当存在多普勒估计错误时，各方法补偿性能都有一定程度的降低，其中信道2小多普勒的补偿性能较好，多次重采样法与本文方法比较接近（多次重采样法低S N R下有稍许波动），但是对于大多普勒扩展的情况，本文方法的补偿性能更加优于其他两种方法，且相对性能提升12.71%，高于仿真1中的情况，这表明本文所提的接收机设计对多普勒估计误差的敏感性要低于其他方法，具有较高的鲁棒性。

4.3 信道信息未知时，各方法补偿性能比较

本组仿真考虑实际的接收机补偿性能，重点比较本文方法与多次重采样方法，所有信道参数对于接收端来说都是未知的，都需要接收端进行估计。图5给出了信道1情况下各方法补偿BE R随S N R的变化曲线（信道2的情况与此类似，本组仿真不再列出），由图中可以看出，最优单次重采样法的补偿性能相对于前两组仿真的趋势没有太大的变化。另外，本文方法的补偿性能仍然优于多次重采样法，且它们的补偿性能随S N R的增大逐渐趋于一致，这是由于随着S N R的增大，信道参数的估计结果逐渐趋于真实值的缘故。

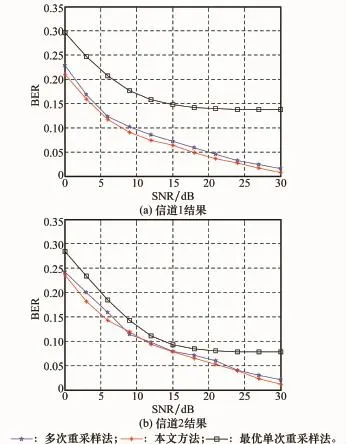
图4 多普勒误差敏感性

图5 信道信息未知时补偿性能

5 结论

水声通信中的非一致多普勒扩展比一致多普勒扩展更接近真实的水声信道，传统多普勒补偿技术一般都假设多径信道各径多普勒因子相等或近似相等，采用单次重采样方法进行补偿，当各径多普勒因子不一致时，会带来较大的残余多普勒扩展。针对此问题，本文在多径信道各径多普勒因子不同的前提下，系统地研究了水声OFDM中的非一致多普勒补偿问题。在详尽的原理推导基础上给出了所提非一致多普勒补偿接收机的结构图及处理步骤，并通过仿真实验验证了所提接收机的以下特点：①在信道参数信息已知与未知的情况下，都具有较高的补偿性能；②非常适合多径传输差异较大的非一致多普勒扩展信道的多普勒补偿。因此，所提接收机设计对于信道时变性较强、存在非一致多普勒扩展的高速移动水声通信具有一定的参考价值。

［1］Baggeroer A.A n overview of acoustic co m m unications fro m 2000-2012［J］.Underw ater Com m unications：Channel M odelling&Validation，2012，5：201-207.

［2］W ang Y L，M a S L，Liang G L，et al.Chirp spread spectrum of orthogonal frequency division multiplexing underwater acoustic communication system based on multi-path diversity receive［J］.Acta-Physica Sinica，2014，63（4）：177-186.（王逸林，马世龙，梁国龙，等.基于多径分集的啁啾扩频正交频分复用水声通信系统［J］.物理学报，2014，63（4）：177-186.）

［3］Ebihara T，Mizutani K.Underwater acoustic communication with an orthogonal signal division multiplexing scheme in doubly spread channels［J］.IE E E Journal of Oceanic Engineering，2014，39（1）：47-58.

［4］Wang Y L，Chen Y，Yin J W，et al.Research on orthogonal multi-carrier underwater acoustic communication system based on fractional Fourier transform［J］.Journal on Communications，2012，33（8）：162-170.（王逸林，陈韵，殷敬伟，等.基于分数阶Fourier变换的正交多载波水声通信系统研究［J］.通信学报，2012，33（8）：162-170.）

［5］Esmaiel H，Jiang D.Review article：multicarrier com munication for underwater acoustic channel［J］.International Journal of Com munications，Network and System Sciences，2013，6（8）：361-367.

［6］Li Y G，Stuber G L.Orthogonal frequency division multiplexing for wireless communications［M］.Springer，2006.

［7］ Berger C R，Zhou S，Preisig J C，et al.Sparse channel estimation for m ulticarrier underwater acoustic co m m unication：fro m subspace methods to co m pressed sensing［J］.IE E E Trans.on Signal Processing，2010，58（3）：1708-1721.

［8］M ason S F，Berger C R，Zhou S，et al.Detection，synchronization，and Doppler scale estimation with multicarrier waveforms in underwater acoustic com munication［J］.IE E E Journal on Selected Areas in Com munications，2008，26（9）：1638-1649.

［9］Aval Y M，Stojanovic M.Partial FF T demodulation for coherent detection of O FD M signals over underwater acoustic channels［C］∥Proc.of the Oceans，2013：1-4.

［10］Sharif B S，Neasham J，Hinton O R，et al.A co m putationally efficient Doppler co m pensation system for underwater acoustic co m m unications［J］.IE E E Journal of Oceanic Engineering，2000，25（1）：52-61.

［11］H uang J，Zhou S，H uang J，et al.Progressive inter-carrier interference equalization for OFDM transmission over time-varying underwater acoustic channels［J］.IE E E Journal of Selected Topics in Signal Processing，2011，5（8）：1524-1536.

［12］Tu K，Fertonani D，Du man T M，et al.Mitigation ofintercarrier interference for OFDM over time-varying underwater acoustic channels［J］.IE E E Journal of Oceanic Engineering，2011，36（2）：156-171.

［13］M ason S，Berger C，Zhou S，et al.A n OFDM design for underwater acoustic channels with Doppler spread［C］∥Proc.of the Digital Signal Processing W orkshop and5th IE E E Signal Processing E ducation W orkshop，2009：138-143.

［14］Li B，Zhou S，Stojanovic M，et al.M ulticarrier com munication over underwater acoustic channels with nonuniform Doppler shifts［J］. IE E E Journal of Oceanic Engineering，2008，33（2）：198-209.

［15］Yerramalli S，Mitra U.Optimal resa m pling of OFDM signals for m ultiscale-m ultilag underwater acoustic channels［J］.IE E E Journal of Oceanic Engineering，2011，36（1）：126-138.

［16］Beygi S，Yerra malli S，Mitra U.Optimal Bayesian resa m pling for OFDM signaling over m ulti-scale m ulti-lag channels［C］∥Proc.of the7th A C M International Conference on Underw ater Networks and Systems，2012：6-11.

［17］Tu K，Du man T M，Stojanovic M，et al.M ultiple-resam pling receiver design for OFDMover Doppler-distorted underwater acoustic channels［J］.IE E E Journal of Oceanic Engineering，2013，38（2）：333-346.

［18］Karakaya B，Hasna M O，Du man T M，et al.Multi-resa m pling Doppler compensation in cooperative underwater OFDM systems［C］∥Proc.of the Oceans，2013：1-8.

［19］John G P，Masoud S.Diqitalcom mubication［M］.5th ed.Zhang L J，Zhang Z C，Song Z F，et altrans.Beij ing：Publishing H ouse of Electronics Industry，2011：428-430.（John G P，M asoud S.数字通信［M］.张力军，张宗橙，宋荣方，等译.5版.北京：电子工业出版社，2011：428-430.）

［20］Q u F Z，Nie X Y，Xu W.A two-stage approach for the estimation of doubly spread acoustic channels［J］.IE E E Journal of Oceanic Engineering，2014，99（1）：1-13.

Non-uniform Doppler compensation in underwater acoustic communication based on O FD M

WANG Biao1，2，DIN G Lu-fei1，Z HI Zhi-fu1，D AI Y ue-wei1
（1.School of Electronic and Information，Jiangsu University of Science and Technology，Zhenjiang 212003，China；
2.Key Laboratory of Underwater Acoustic Warfare Technology，Beijing 100094，China）

When there is different Doppler factors in each path of multi-path channel，the traditional Doppler compensation techniques will bring large residual Doppler spread.To solve the problem，a compensation method for non-uniform Doppler spread through a theoretical derivation is proposed，which uses multiple interpolation combined with the fast Fourier transform（FF T）algorith m.After a single resampling preprocessing aiming to reduce the size of the Doppler factor，an equivalent channel parameter modelis considered.Further，to demodulate the orthogonal frequency-division multiplexing（OFDM）data，channel statistics are obtained by multiple interpolation and FF T.Numerical simulation results show that the proposed method has a high Doppler compensation performance both in know n or unknown channel information.Especially w hen the non-uniform Doppler spread is serious，the performance of the method is much better than others.

underwater acoustic communication；Doppler compensation；orthogonal frequency-division multiplexing（OFDM）；time-varying channel

T N 911.5

10.3969/j.issn.1001-506 X.2016.03.30

1001-506 X（2016）03-0672-07

2014-11-04；

2015-09-23；网络优先出版日期：2015-10-20。

网络优先出版地址：http：//w w w.cnki.net/kcms/detail/11.2422.T N.20151020.1334.006.html

国家自然科学基金（11204109，11574120）；水声对抗国防重点实验室基金；江苏省高校优势学科建设工程；江苏省“青蓝工程”资助课题

王彪（1980-），男，副教授，博士，主要研究方向为水声通信。

E-mail：mail-wb@163.com

丁鹭飞（1991-），女，硕士研究生，主要研究方向为水声通信。

E-mail：dlfqm@qq.com