基于改进BPSO的聚类选择性集成

2016-09-20王晓丹邢雅琼空军工程大学防空反导学院陕西西安710051

系统工程与电子技术 2016年3期

毕凯，王晓丹，邢雅琼（空军工程大学防空反导学院，陕西　西安710051）

基于改进BPSO的聚类选择性集成

毕凯，王晓丹，邢雅琼
（空军工程大学防空反导学院，陕西西安710051）

首先针对离散二进制粒子群（binary particle swarm optimization，BPS O）容易陷入局部收敛的问题，提出一种改进的BPS O算法。在分析高斯密度函数对尺度敏感性的基础上，利用粒子群与全局最优粒子的一致性动态调节尺度参数，并利用密度函数对称区间的定积分确定全局最优粒子的变异概率。而后将聚类的选择性集成抽象为组合优化问题，利用聚类成员有效性和差异性的加权组合定义适应度并以改进BPS O的进化过程实现聚类的选择性集成。最后基于标准数据集和图像数据集验证算法的有效性。

聚类选择性集成；离散二进制粒子群；高斯密度函数；图像分割

网址：w w w.sys-ele.co m

0 引言

聚类集成是指无监督情况下对同一数据集多种不同聚类结果的决策级融合。由于具有鲁棒性、新颖性、稳定性、并行性以及可扩展性等优点［1］，使其一经提出便受到普遍关注，已成为当前聚类研究的重要方向并成功应用于图像分割［2］、文本分类［3］、特征提取［4］、生物工程［5］等诸多领域。

文献［6］于2002年首次提出选择性集成学习的概念，并通过理论分析和实验表明具有较好分类性能和较大差异性的基分类器更有利于构造高性能的强分类器。与有监督集成学习类似，聚类的选择性集成已被提出并广泛研究。聚类法和排序法是当前常用的两种聚类选择性集成方法［7］。聚类法［7-8］首先以差异性作为划分依据，通过聚类算法使差异性较小的聚类成员划为同类，而差异性较大的聚类成员分为异类，而后在各类别中选择有效性最高的聚类成员用于集成。排序法［9-10］则利用线性组合将有效性和差异性统一为适应度，并依据适应度的大小对全体聚类成员进行排序，而后利用适应度最高的聚类成员用于集成。

需要指出的是，上述聚类选择性集成方法虽然取得了一定研究进展，但仍存在以下问题：①聚类法中聚类算法的选择。聚类算法通常基于特定的数据结构假设，当真实数据与假设相符时能够获得良好的划分结果，当不符时划分结果与实际相差甚远。全体聚类成员的空间结构通常是未知的，这将使聚类算法的选择具有较大盲目性；②排序法中利用任一聚类成员与其余全体聚类成员间的平均差异性描述差异性，但选择出聚类集合的整体差异性利用该描述存在一定误差；③无论是聚类法还是排序法都需要确定选择规模，而选择规模通常与实际问题、全体集成规模和聚类成员的质量等问题有关，因而人为设定选择规模稍欠合理。

为解决上述问题，本文将聚类的选择过程看作是组合优化问题，提出一种基于离散二进制粒子群（binary particle swarm optimization，BPS O）的聚类选择性集成方法。首先为避免陷入局部最优解，给出一种基于改进高斯变异的离散粒子群进化算法，而后利用聚类成员有效性和差异性的加权组合定义适应度，并基于改进离散粒子群的进化过程实现聚类的选择性集成。

1 改进的BPSO

1.1 BPSO

粒子群优化算法（particle swarm optimization，PSO）［11］是Kennedy和Ebethart于1995年提出的一种基于群体智能的随机寻优算法。通过对鸟群社会行为进行模拟，在多维解空间中利用一定规模的可行解构成粒子群，并通过粒子间的相互作用，对解空间进行智能搜索，从而发现最优解。由于具有原理简单、易于实现、收敛速度快、群体搜索、协同搜索以及通用性强等优点，近年来相关研究发展迅速。

设搜索空间为d维，群体中第i个粒子的位置为Xi= （xi1，xi2，…，xid），速度为Vi=（vi1，vi2，…，vid），它经历过的最佳位置为Pi=（pi1，pi2，…，pid），群体经历过的最佳位置为Pgbest=（pg1，pg2，…，pgd）。粒子分别按式（1）和式（2）更新自己的位置和速度：

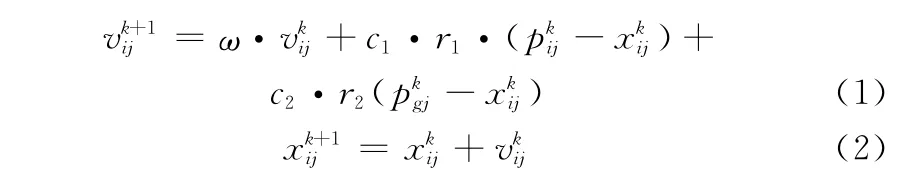
式中，ω为惯性权重，较大时适于对解空间进行较大范围搜索，较小时适于进行小范围搜索；k为迭代次数；r1，r2为（0，1）之间的随机数；c1，c2为加速因子，通常取2。每一维的位置和速度都被限制在一定的范围内，粒子飞行过程中如果位置和速度超过边界范围则取边界值。Pi和Pgbest不断更新，最后输出的Pgbest就是全局最优解。

BPSO是PSO的离散二进制版本，于1997年由Kennedy 和Ebethart提出［12］，开启了PS O算法在离散问题领域的应用。在二进制编码中，BPS O限制粒子位置只能取0或1，需要指出的是，二进制粒子群算法中速度向量不再是位置变化，而仅表示概率，即每一维分量的取值为1或0的概率，引入模糊函数sigmoid：

利用式（4）替代式（2），有

式中，rand为［0，1］间的随机数，通过分析可以发现当最大飞行速度大于10时，sig（v）将趋近于0，为防止该函数趋近于0，可将速度限制于［-4，4］区间内［13］。

1.2 改进BPSO

为避免BPS O可能陷入局部最优，出现所谓的早熟现象，文献［14］通过自适应扰动惯性因子来增强粒子群跳出局部最优的能力，文献［15］提出通过增加粒子群的多样性，以达到摆脱群体陷入局部极值的可能。需要指出的是，上述文献均基于连续PS O算法易陷入局部极值的问题提出，而离散PS O的进化过程与连续PS O存在较大区别［16］。

分析BPS O的进化过程可以看到，粒子通过跟踪个体极值Pi和群体极值Pgbest来更新自己，当某一粒子发现一个局部最优值，则其他粒子将迅速向其靠拢，此时粒子群可能陷入局部最优。因而可以考虑通过对Pgbest进行适当扰动以达到跳出局部极值并提高算法精度的目的［17］。

高斯变异是标准进化规划中常用的变异算子［18］，标准高斯分布密度为N（0，1），期望为0，方差为1。对于个体X=（x1，x2，…，xd），经过变异后得到一个新的个体X′= （x′1，x′2，…，x′d），其变异过程可描述为

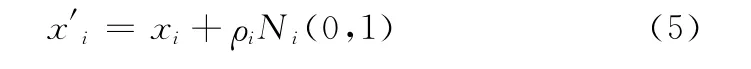
考虑高斯概率密度函数的一般形式

式中，μ∈R，σ∈R+。密度函数p（x）的图形如图1所示。观察可知，μ决定了密度函数的位置，σ的取值对高斯密度函数的形状具有重要意义。σ越小函数图像越收拢，x以较高概率分布于x=μ附近，σ越大则函数图像越发散，x的分布则相对发散。不考虑密度函数的位置，本文令μ=0。

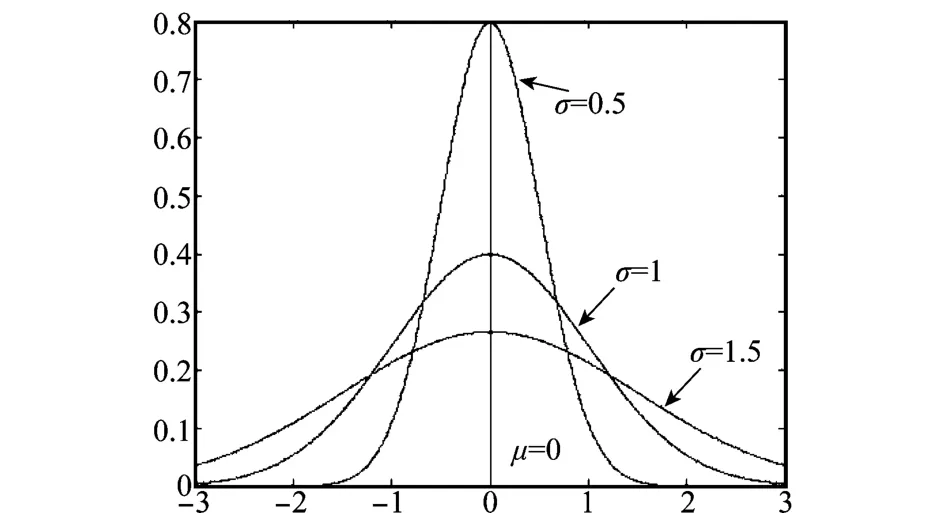
图1 高斯概率密度函数

由式（6）可知，x在全体实数范围内取值，而在BPS O中变异本质上是以一定的概率取反，为实现变异进行如下讨论。

令F（x）表示变异概率

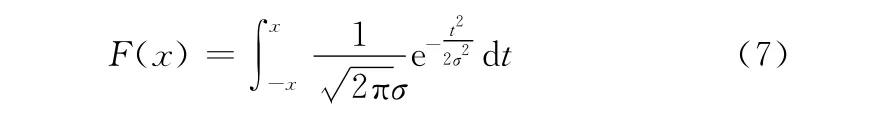
分析可知，对于任意的x∈（0，+∞），F（x）∈（0，1）。对于确定的x，F（x）为σ的单调减函数，当σ→0时，F（x）→1，当σ→+∞时，F（x）→0。考虑到BPS O进化过程的不同变异需要，这里定义动态的σ。

式中，λ为缩放系数，用于控制σ（k）的变化范围；ξ为略小于1的数，xij==pgj用于判断二者是否相等，若相等取值为1，否则取值为0。分析式（8）可知，在进化的初始阶段，k值较小且各粒子与全局最优解的一致性较弱，因而σ（k）取值较小使Pgbest具有较高的变异概率，进而使种群可在较旷阔空间内进行搜索。随着进化过程不断进行，1-ξk取值趋近于1，各粒子不断向全局最优解靠拢，σ（k）取值不断增加，使得变异概率降低，避免过度变异而错过全局最优解。基于上述分析并参考式（4），则全局最优解Pgbest的变异操作可表示为

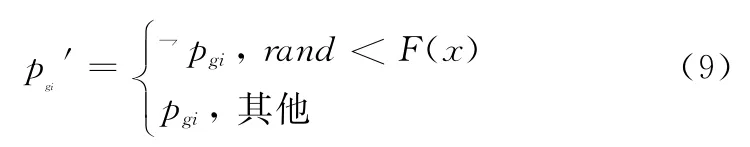
此外，考虑到惯性权重ω对进化过程的非线性影响，采用文献［19］的策略，采用非线性方法自适应调整惯性权重ω。具体公式为

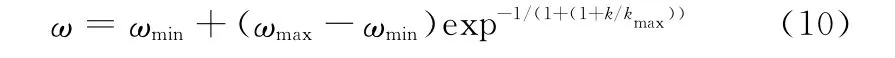
综上改进的BPS O算法流程可表示如下。

算法1 改进的BPS O

输入最大迭代次数km ax；粒子群规模T；收敛阈值d；加速因子c1、c2；惯性权重ωm ax，ωmin；变异次数n；缩放系数λ；积分区间x。

输出最优解Pgbest。

步骤1 随机初始化速度和各粒子位置；

步骤2 计算适应度，标记各粒子为经历过最佳位置Pi，将适应度最高粒子标记为全局最佳位置Pgbest；

步骤3 判断算法是否满足收敛条件（最大适应度或最大迭代次数要求），若满足转向步骤7；

步骤4 利用式（10）计算惯性权重，利用式（1）更新粒子飞行速度，利用式（3）、式（4）更新粒子位置；

步骤5 计算各粒子适应度，若Pi和Pgbest优于历史最佳位置，则更新Pi和Pgbest；

步骤6 利用式（7）～式（9）对Pgbest进行变异，并计算适应度，若优于则更新Pgbest，并转向步骤3，否则直接转向步骤3；

步骤7 输出算法最优解Pgbest。

2 基于改进BPSO的聚类选择性集成

2.1 聚类选择性集成的问题描述

聚类集成通常可描述为：设数据集合Y=｛y1，y2，…，yN｝，N为数据规模，Π=｛π1，π2，…，πM｝为数据集Y上M个独立的聚类结果，其中πi=｛ci1，ci2，…，ciki｝为聚类成员，ki为类别数。对于任意y，若y∈cij则表示该数据点在第i个聚类成员中类别为j。聚类集成本质上是利用合理的方法对M个独立聚类结果的一致性分析和决策。

聚类成员有效性和差异性对于集成结果具有十分重要的影响。有效性用于保障聚类成员的基本正确率，全集成结果、聚类成员的全部结果等集成趋势通常被作为有效性评价的客观标准［7 9］。此外还有方法通过分析聚类结果与数据集合的空间结构相似性确定其有效性，如轮廓指标（Silhouette index）、Dunn指标、Davies-Bouldin指标、Gap统计等［10］。差异性其目的在于使各聚类成员的错误相互独立，通过集成使正确划分不断积累而错误划分相互抵消。调整的兰德指数（adjusted rand index，A RI）、规范化互信息（normalized mutualinformation，N MI）、信息熵（entropy）、条件熵（conditional entropy）、Double Fault Measure、Coincident Fai lure Diversity、Measurement of Inter-Rater Agreement等通常被用于描述聚类成员间差异性。

有效的聚类选择性集成通常基于有效性和差异性的综合考虑，如文献［8］利用重采样技术（resampling technique，R T）通过对比聚类算法在整体数据集和随机数据子集的分类一致性确定该聚类成员的有效性，利用Rand index计算任意聚类成员与其他聚类成员的差异性之和，文献［9］中利用N MI和A RI评价聚类成员的有效性，同时利用N MI计算任意两聚类成员间的差异性，文献［10］在对多种内部评价方法进行分析的基础上给出了一种组合有效性评价方法，并将其与基于Jaccard的差异性方法联合选择聚类成员。

2.2 基于改进BPSO的聚类选择性集成

聚类的选择性集成过程可抽象为0-1组合优化问题，1表示聚类成员被选择，0表示聚类成员未被选择。对于规模为M的聚类集成，其选择问题的规模为2M，虽然利用分支定界法能够求得全局最优组合，但算法复杂度较高，难以应用于实际问题。这里利用算法1所述改进的BPSO算法，通过离散粒子群进化过程实现聚类成员的选择。

如第2.1节所述，有效性和差异性对集成结果具有重要影响。对于聚类算法，由于缺乏必要的先验信息，通常难以准确评价其有效性。这里令π*表示全体聚类成员的集成结果，假设π*能够表示更为合理的数据类别划分，考虑利用π*作为聚类有效性评价的参考划分，利用N MI度量任意聚类成员πi与π*间一致性，则有效性可描述为

其值越大表示πi与π*的一致性越高，即πi的有效性越高，其值越小则表示πi的有效性越低。同样考虑N MI描述选择出聚类成员子集的整体差异性

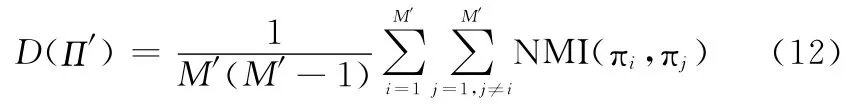
Π′为规模为M′的聚类成员子集，πi，πj∈Π′。与有效性描述相反，D（Π′）其值越小表示聚类成员子集的差异性越大，反之则差异性越小。通过对聚类有效性和差异性的加权线性组合，以获取单一目标的集成适应度函数，其表示为

式中，α为有效性和差异性的权重调节因子，用于平均二者的影响，文献［8］指出其值取0.5更有利于获得较好选择集成结果。

在BPSO算法中，初始种群通常随机产生，因此初始的最优粒子也是随机的，这可能使得它一开始就严重偏离最优粒子，延缓进化速度。如果粒子群一开始就掌握了一个较优解，使得粒子群一开始就朝着比较合理的方向进行搜索，这样必然会缩短粒子群的进化过程。因此在粒子群的初始化阶段，可利用式（11）计算全体聚类成员的有效性，将有效性最高的m个聚类成员标记为选择，以保证初始进化的较合理方向。综上基于改进BPSO的聚类选择性集成过程可描述如下。

算法2 基于改进BPS O的聚类选择集成

输入数据集合、聚类成员生成方法G、集成方法E、集成规模M、平衡因子α、初始选择规模m及算法1相关参数。

输出选择性集成结果。

步骤1 利用方法G生成规模为M的全体聚类成员πi，利用集成方法E（如文献［1］中基于相似分割的聚类算法（cluster-based similarity partitioning algorithm，CSPA）、变换图算法（meta-clustering algorithm，M CL A）、超图划分算法（hypergraphpartitioning algorithm，H GPA）等求取全集成结果π*；

步骤2 利用式（11）计算全体聚类成员πi的有效性；

步骤3 标记有效性最高的前m个聚类成员位置为1，并初始化全局最优解Pgbest，随机初始化T-1个粒子；

步骤4 利用算法1求解全局最优解Pgbest；

步骤5 选择Pgbest所对应聚类成员，利用集成方法E进行求解，获得选择性集成结果。

3 实验与验证

为验证本文所提聚类选择集成方法的有效性，分别在标准数据集和图像数据集进行实验。

3.1 标准数据集实验

实验数据为11组U CI标准数据集，其详细描述如表1所示。

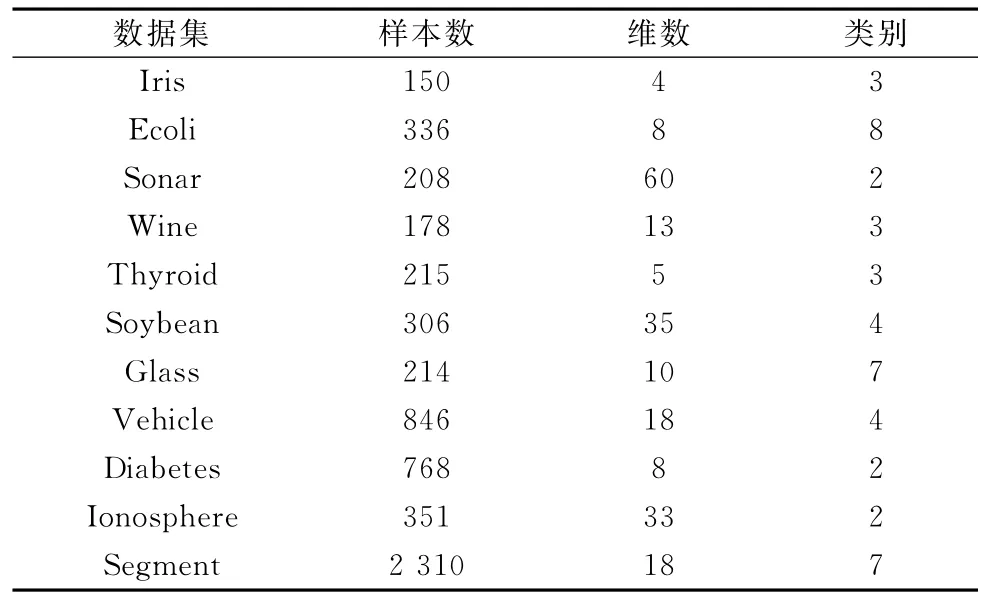
表1 实验数据描述

通过对谱聚类（nystrm spectral clustering，NSC）算法进行采样和尺度参数扰动生成差异性聚类成员，采样规模为50，尺度参数扰动范围为［0.1，0.6］。改进BPSO中令最大迭代次数为100，初始速度为0，群体规模为30，加速因子均取2，惯性权重分别为0.9和0.4，变异次数为30，缩放系数为10，积分区间为1，初始选择规模为20。集成算法采用文献［1］中描述的CSPA和M CLA，全集成规模为50，平衡因子α为0.5。以集成结果与标准类标签的F M（Fowlkes Mal lows，F M）指标作为评价标准

对于两划分π1，π2，a表示既属于π1中同一聚类，又属于π2中同一聚类的样本对个数，b表示属于π1中同一聚类，但不属于π2中同一聚类的样本对个数，c表示不属于π1中同一聚类，但属于π2中同一聚类的样本对个数。F M指标越大，表明两划分结果越接近，反之亦然。

实验1 首先就改进BPSO算法的收敛性和有效性进行分析，实验数据包括Iris、Ecol i、Sonar、Ionosphere 4个数据集，对比算法包括BPSO、混沌BPSO1（chaotic BPSO，CBPSO1）和CBPSO2［20］，实验结果如图2所示。

图2 多种离散粒子群算法在4个数据集上适应度与迭代次数关系

分析图2可以看到，在4个标准数据集上，与BPSO、CBPSO1和CBPSO2相比，本文所提改进的离散粒子群算法—gBPSO能够发现更优的Pgbest；收敛速度方面，BPSO与CBPSO1相当，gBPSO次优，CBPSO2收敛速度最快，但可以看到CBPSO2较快的收敛速度是由于其陷入局部最优解无法跳出而得到的。综上可见本文所提方法更能够兼顾收敛性和有效性。

实验2 为验证本文所提聚类选择性集成方法的有效性，在表1所示标准数据集上进行验证，考虑到M C L A较高的有效性，实验中均以M C L A全集成结果作为有效性参考，利用CSP A和M C L A的全集成和选择性集成结果分别如表2和表3所示，由于CSP A仅适用于规模小于1 000的数据集，因而表2未给出Seg ment数据集实验结果。表2和表3中全集成方法（all cluster ensemble，A E）为全集成结果，选择聚类集成算法（select cluster ensemble，SCE）为文献［7］中利用集成适应度排序的聚类选择性集成，基于协方差的聚类集成算法（cluster select ensemble based on covariance，CSE V）为文献［22］中基于协方差矩阵的聚类选择性集成，BPSO、CBPSO1、CBPSO2、gBPSO分别为利用不同的粒子群算法进行选择性集成的结果，选择规模均为20，表中数据均为20次独立重复实验的均值，最优选择集成结果被加粗。

表2 标准数据集聚类选择性集成结果（CSPA）

表3 标准数据集聚类选择性集成结果（M CL A）

分析上述实验结果，首先将选择性集成结果与全集成结果进行对比可以看到，SC E、CSR V、BPS O、CBPS O1、CBPS O2、gBPS O 6种选择性集成方法分别在6/6、6/6、6/7、7/ 5、6/7、7/9个数据集上取得优于全集成的聚类结果，表明对聚类成员的适当选择是进一步提高聚类集成精度的有效途径。进一步，将本文所提方法与其他5种选择方法进行对比可以看到，gBPS O在5/4个数据集上取得最优聚类选择集成结果，在2/2个数据集上取得次优聚类选择集成结果，优于其他选择性集成方法。

综上，基于标准数据集的实验结果显示本文所提gBPSO不仅具有较快的收敛速度和全局寻优性能，同时将其应用与聚类的选择性集成也取得了较高的分类正确性。

3.2 图像数据集实验

为进一步验证本文所提选择性集成方法的正确性，在图像数据集上进行分割实验，实验结果如图3所示。

图3 分割实验图像

实验3 合成纹理图像分割，实验图像如图3（a）所示，为一5类合成纹理图像，图像大小为256×256。利用11×11中值滤波器、2种高斯差分（difference of Gaussian，D O G）滤波器和6种高斯偏移差分（difference of offset Gaussian，D O O G）滤波器（见图4）共提取9维特征信息。

图4 D O G和D O O G滤波器示意图

利用N SC、N SC+M C L A、N SC+SC E+M C L A（选择规模为20）、N SC+gPS O+M C L A进行分割，上述集成算法中利用随机采样和扰动尺度参数生成聚类成员，采样规模为100，尺度扰动范围［0.1，0.6］，全集成规模为30，其他参数设置与3.1节相同，图像分割结果如图5所示。

图5 纹理图像分割结果

在图5中将利用改进粒子群算法进行聚类选择性集成的分割结果（如图5（d）所示）与其他方法的分割结果进行对比可以看到，选择后的分割结果不仅能够一定程度上消除分类误差（如图中下方区域），而且能够更好描述分割的边界区域。

实验4 SA R图像分割，实验图像如图3（b）所示，为美国华盛顿特区波托马克河的局部描述，图像大小为150× 150，图中主要地物包括河流、植被以及人工建筑。对该图像提取基于3层非下采样小波分解的10维能量特征组成特征空间［21］，为更好描述图像信息，观测窗口为7×7。这里固定谱聚类尺度参数为0.1，通过差异性采样生成不同的分类结果，采样规模为100，全集成规模为30，图像分割结果如图6所示。

图6 SAR图像分割结果

分析图6，首先将3幅集成分割图像（b）（c）（d）与单聚类分割图像（a）进行对比，可以看到集成分割能够将河岸人工建筑物区分开来，究其原因，采样数据点的质量对于N SC聚类结果具有重要影响，当对图像中人工建筑物的采样不足时，可能造成对其的错分，将多次基于随机采样的分类结果进行集成，能够有效避免单次采样的不足，具有更好的图像分类能力；进一步对比3幅集成图像可以看到，图6（c）在河流中心岛屿的分类中存在明显的杂斑，且对于河岸建筑的分类较为粗糙，整体效果劣于图6（b）和图6（d），而图6（d）与图6（b）对于河岸的分类效果相当，但在河流中心岛屿中桥梁和岛边缘的错分上，图6（d）明显优于图6（b），可见本文方法对于图3（b）具有更好的分割效果。

4 结论

本文首先针对BPS O易于陷入局部极值，利用高斯密度函数上对称区间的定积分表示变异概率并通过扰动全局最优粒子以实现跳出矩阵最优的目的。考虑到高斯密度函数的尺度敏感性，利用迭代次数和粒子群与全局最优的一致性自适应调节尺度参数。而后将聚类的选择性集成问题抽象为组合优化问题，定义聚类成员的有效性、差异性以及适应度函数，通过粒子群的进化过程实现聚类成员的选择。实验结果验证了本文方法的有效性。

［1］Strehl A，G hosh J.Cluster ensem bles-a knowledge reuse framework for combining multiple partitions［J］.Journal of Machine Learning Research，2002，3（3）：583-617.

［2］Jia J H，Liu B X，Jiao L C.Soft spectral clustering ensem bleapplied to image segmentation［J］.Frontiers of Computer Science in China，2011，5（1）：66-78.

［3］Lu Z M，Li C，Zhang Q.A document cluster ensemble spectral algorithm based on affinity propagation［J］.Journal of Harbin Engineering University，2012，33（7）：899-905.（卢志茂，李纯，张绮.近邻传播的文本聚类集成谱算法［J］.哈尔滨工程大学学报，2012，33（7）：899-905.）

［4］Hong Y，K wong S，Chang Y，et al.Unsupervised feature selective clustering ensembles and population based incrementallearning algorithm［J］.Pattern Recognition，2008，41（9）：2742-2756.

［5］H u X，Park E，Zhang X.Microarray gene cluster identification and annotation through cluster ensemble and E M-based informative textual summarization［J］.IE E E Trans.on Information Technology in Biomedicine，2009，13（5）：832-840.

［6］Zhou ZH，W u J X，Tang W.Ensem bling neural networks：many could be better than all［J］.ArtificialIntelligence，2002，137（1-2）：239-263.

［7］Fern X Z，LinW.Cluster ensem ble selection［J］.Statistical Analysis and Data Mining，2008，1（1）：128-141.

［8］Zhang C X，Zhang J S.A survey of selective ensem ble learning algorithm［J］.Chinese Journal of Com puters，2011，34（8）：1399-1410.（张春霞，张讲社.选择性集成学习算法综述［J］.计算机学报，2011，34（8）：1399--1410.）

［9］H ong Y，Sam K，W ang H L，et al.Resam pling-based selective clustering ensembles［J］.Pattern Recognition Letters，2009，30 （3）：298-305.

［10］Naldi M C，Carvalho A C，Campello R J.Cluster ensemble selection based on relative validity indexes［J］.Data Mining& Knowledge Discovery，2013，27（2）：259-289.

［11］Kennedy J，Eberhart R C.Particle swarm optimization［C］∥Proc.of the IE E E International Conference on N eural Networks，1995：1942-1948.

［12］Kennedy J，Eberhart R C.A discretebinary version of the particle swarm algorith m［C］∥Proc.of the World Multiconferenceon Systemics，Cybernetics and Inform atics，Piscata way，1997：4104-4109.

［13］Fan K，Zhang R Q，Xia G P.Solving a class of job-shop schedul ing problem based on improved BPSO algorithm［J］.Systems Engineering-Theory&Practice，2007，27（11）：111-117.（樊坤，张人千，夏国平.基于改进BPSO算法求解一类作业车间调度问题［J］.系统工程与理论实践，2007，27（11）：111-117.）

［14］Alberto GV，Rafael P.Introducing dynamic diversity into a discrete particle swarm optimization［J］.Computer and Operation Research，2009，36（3）：951-966.

［15］Zhang C S，Sun J G，Ouyang D T.A self-adaptive discete particle swarm optimization algorithm［J］.Acta Electronica Sinica，2009，37（2）：298-304.（张长胜，孙吉贵，欧阳丹彤.一种自适应离散粒子群算法及其应用研究［J］.电子学报，2009，37（2）：298-304.）

［16］Tao X M，W ang Y，Zhao C H，et al.Discrete particle swarm optimization based on double-scale cooperationm utation［J］. Journalof H arbin Engineering University，2011，32（12）：1617 -1623.（陶新民，王妍，赵春晖，等.双尺度协同变异的离散粒子群算法［J］.哈尔滨工程大学学报，2011，32（12）：1617-1623.）

［17］Yao X，W ang X D，Zhang Y X，et al.Feature selection algorith m using PSO with adaptive mutation-basedtdistribution［J］.Systems Engineering and Electronics，2013，35（6）：1335-1341.（姚旭，王晓丹，张玉玺，等.基于自适应t分布变异的粒子群特征选择方法［J］.系统工程与电子技术，2013，35（6）：1335-1341.）

［18］Zhou F J，W ang X J，Zhang M.Evolutionary progra m ming using mutations based on thetprobability distribution［J］.Acta Electronica Sinica，2008，36（4）：667-671.（周方俊，王向军，张民.基于t分布变异的进化规划［J］.电子学报，2008，36（4）：667-671.）

［19］Gao Y L，Ren Z H.Adaptive particle swarm optimization algorithm with mutation operator［J］.Com puter Engineering and Applications，2007，43（25）：43-47.（高岳林，任子晖.带有变异算子的自适应粒子群优化算法［J］.计算机工程与应用，2007，43（25）：43-47.）

［20］Chuang L Y，Yang C S，W u K C，et al.Gene selection and classification using taguchi chaotic binary particle swarm optimization［J］.E xpert Systems with Applications，2011，38（10）：13367-13377.

［21］Kersten P B G，Lee J S，Ainsworth T L.U nsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and E M clustering［J］.IE E E Trans.on Geoscience and Remote Sensing，2005，43（3）：519-527.

［22］Lu X Y，Yang Y，W ang H J.Selective clustering ensemble based on covariance［C］∥Proc.of the11th International Workshop，2013：179-189.

Cluster ensemble selection based on improved BPSO

BI Kai，W A N G Xiao-dan，XIN G Ya-qiong
（School of Air and Missile Defense，Air Force Engineering University，Xi’an 710051，China）

At first，as binary particle swarm optimization（BPS O）relapses into local extremism easily，an improved BPS O is proposed.By analyzing the scale sensitivity of Gaussian density function，the scale parameter is regulated based on the consistency between particle swarm and the global optimal particle.The mutation probability of the global optimal particle is determined by the definite integral in symmetric interval of the Gaussian density function.Then，the cluster ensemble selection is modeled as a combinatorial optimization problem.The fitness of each cluster memberis defined by weighted co m position of effectiveness and difference，and the cluster ensemble selection is carried out based on the mimproved BPS O.Finally，experiments on standard dataset and image dataset show that the proposed method is effective.

cluster ensemble selection；binary particle swarm optimization（BPS O）；Gaussian density function；image segmentation

T P 391

10.3969/j.issn.1001-506 X.2016.03.33

1001-506 X（2016）03-0692-07

2015-01-28；

2015-06-17；网络优先出版日期：2015-09-01。

网络优先出版地址：http：//w w w.cnki.net/kcms/detail/11.2422.T N.20150901.0928.006.html

国家自然科学基金（60975026，61273275）资助课题

毕凯（1985-），男，博士研究生，主要研究方向为智能信息处理、机器学习。

E-mail：bk3039633@163.com

王晓丹（1966-），女，教授，博士研究生导师，主要研究方向为智能信息处理、机器学习。

E-mail：sh milyqq520@163.com