分数阶反向累加离散灰色模型及其应用研究

2016-09-20刘解放刘思峰吴利丰方志耕河南科技学院数学科学学院河南新乡453003南京航空航天大学经济与管理学院江苏南京10016

系统工程与电子技术 2016年3期

刘解放，刘思峰，吴利丰，方志耕（1.河南科技学院数学科学学院，河南　新乡453003；.南京航空航天大学经济与管理学院，江苏　南京10016）

分数阶反向累加离散灰色模型及其应用研究

刘解放1，2，刘思峰2，吴利丰2，方志耕2
（1.河南科技学院数学科学学院，河南新乡453003；
2.南京航空航天大学经济与管理学院，江苏南京210016）

为了减小离散灰色预测模型解的扰动界，增加模型的解的稳定性，并且充分利用系统的新信息，提出了分数阶反向累加离散灰色模型。通过数学推导，给出了模型具体的计算公式，并计算了其扰动界。通过比较一阶反向累加离散灰色模型和分数阶反向累加离散灰色模型扰动界的大小，证明了分数阶反向累加离散灰色模型的优越性。最后，将其应用在某型号武器系统的储存可靠性的预测中，计算结果优于传统灰色预测模型，预测精度有了大幅度提高，从而拓展了灰色预测模型的理论研究和实际应用范围。

灰色预测；分数阶；反向累加；可靠性

网址：w w w.sys-ele.co m

0 引言

灰色系统理论主要研究“小样本、贫信息”问题，近年来得到了学者们广泛的关注和研究［1-8］。灰色系统理论最基本的方法是灰色生成，生成是建立灰色模型的基础。累加生成是使灰色过程由灰变白的一种方法，其在灰色系统理论中占有极其重要的地位。通过累加生成可以看出灰量积累过程的发展态势，使离乱的原始数据中蕴含的积分特性或规律充分表现出来。

对于非负离散序列X（0），其一次累加生成序列X（1）是单调递增的，因此，其拟合曲线（1）也应该是单调递增的才合理。但是，对于单调递减的离散序列X（0），由于X（1）是单调递增的，其模拟序列（1）也是单调递增的，那么在对＾X（1）进行累减生成还原时，就会产生不合理的计算误差，基于此，文献［9］提出了反向累加生成G O M（1，1）模型，由于反向累加生成序列为单调递减序列，因此，在对于单调递减序列进行建模时能取得优于G M（1，1）的计算效果。文献［10-11］提出了参数的直接求解方法，简化了计算过程，并将其应用到了农药降解问题的建模中，取得了优于原始G O M（1，1）的计算精度。在此基础上，文献［12］对于G O M（1，1）模型的初值和背景值进行改进，进一步优化了G O M（1，1）模型的参数求解方法，提高了模型的计算精度。文献［13］给出了模型优化的背景值，不仅提高了建模的精度，而且使得新模型对于递减和递增序列都适用，拓展了新模型的适用范围。在文献［14-15］离散G M（1，1）模型的基础上，文献［16］提出了离散G O M（1，1）模型，并给出了新模型的求解方法，证明了新模型具有白化指数律和线性不变性。上述对于G O M（1，1）模型的改进，改善了该模型的计算效果，扩大了其适用范围，对于灰色理论的发展具有积极的理论和实际意义。

文献［17-18］把分数阶的思想引入到灰色建模中，取得了不错的效果。为了减小灰色预测模型的扰动界，增加模型的稳定性，并且充分利用系统的新信息，提出了分数阶反向累加离散灰色模型，并将其应用在某型号武器系统的储存可靠性预测中，计算结果显示，新模型的计算精度优于传统灰色预测模型，从而拓展了灰色预测模型的理论研究和实际应用范围。

1 一阶反向累加离散灰色模型及其扰动分析

定义1 设原始非负序列X（0）=｛x（0）（1），x（0）（2），…，x（0）（n）｝为原始序列，X（1）=｛x（1）（1），x（1）（2），…，x（1）（n）｝为X（0）的一阶反向累加生成序列，其中

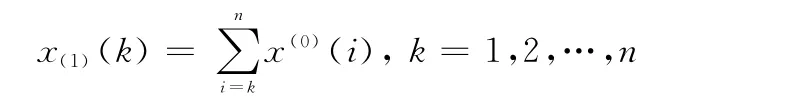
则称

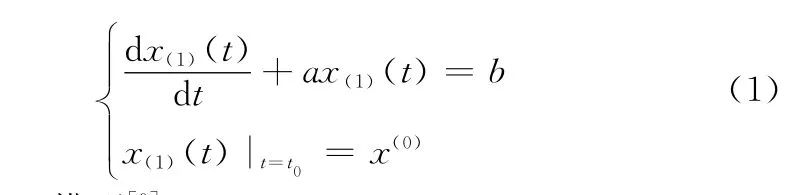
为G O M（1，1）模型［9］。

定理1［19-20］设A∈Cm×n，b∈Cm，A是矩阵A的广义逆矩阵，当A的列向量线性无关时，方程‖Ax-b‖有唯一解。

定理2［19-20］设A∈Cm×n，b∈Cm，A是矩阵A的广义逆矩阵，B=A+F，c=b+k∈Cn，假设方程‖Bx-c‖2= min与‖Ax-b‖2=min的解分别为x+h和x，若rank（A）= rank（B）=n，而且当‖A‖2‖F‖2＜1时，有

其中

称x（1）（k+1）=β1x（1）（k）+β2（k=1，2，…，n-1）为一阶反向累加离散灰色模型。

定理3 一阶反向累加离散灰色模型

x（1）（k+1）=β1x（1）（k）+β2（k=1，2，…，n-1）的参数β1，β2可以利用最小二乘估计来计算，即

定义2 设原始非负序列为

一阶反向累加序列为

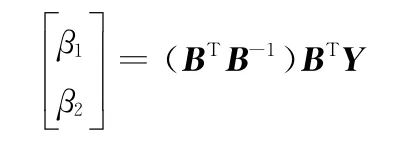
其中

证明略。

定理4 离散灰色模型的解可以按照最小二乘法‖Y-Bx‖2=min进行求解，假设模型的解为x。下面考虑系统存在扰动的情况，为了证明简便，不妨假设系统的第二项有扰动，即（0）（2）=x（0）（2）+ε，那么，解的扰动界为

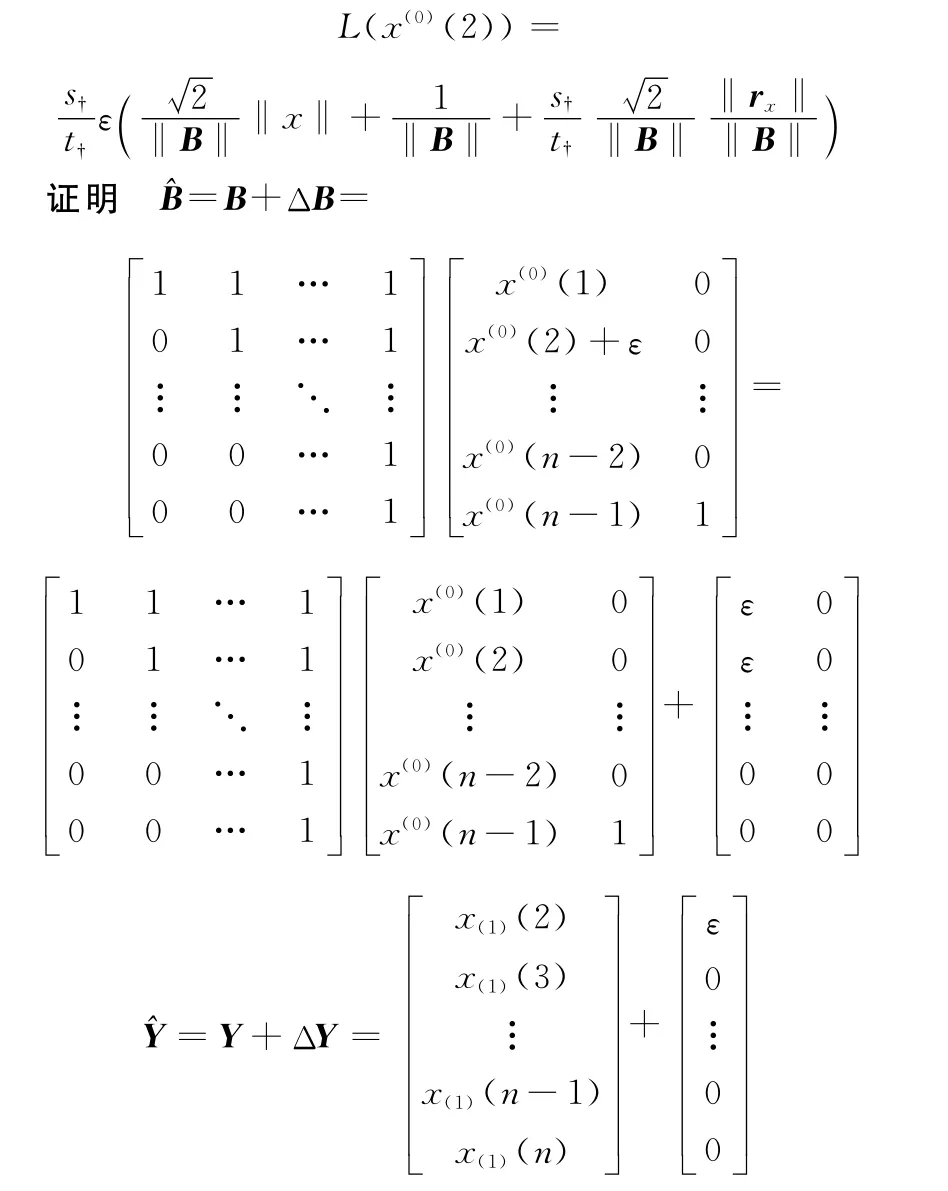
由于B的列向量线性无关，因此，方程‖Y-Bx‖2= min有唯一解x=YB。

因为

又因为

所以

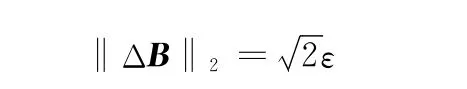
根据定理2，可以得到

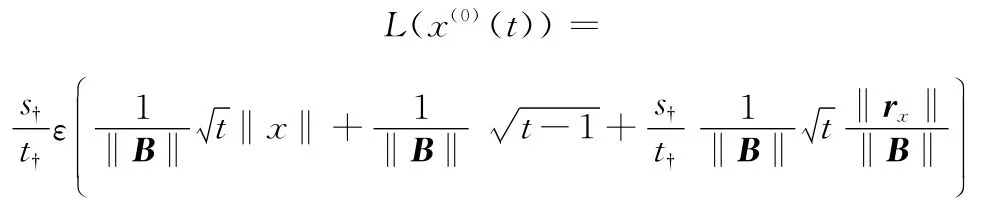
限于篇幅，此处不再具体推导。

从L（x（0）（t））的计算公式可以看出，其扰动界是数据量t的增函数，即

则，系统的扰动界呈现出递增的特性，那么，当新信息发生扰动之后，其扰动界会大于老信息发生扰动之后产生的扰动界，说明模型对于新信息的变化更加敏感，这和灰色系统理论的“新信息优先原理”比较相符。因此，与正向累加生成相比，反向累加生成具有一定的优越性。

2 r阶反向累加离散灰色模型及其扰动分析

为了进一步分析分数阶反向累加离散灰色模型的性质，增加模型解的稳定性，减小灰色预测模型的扰动界，本节建立了r阶分数阶反向累加离散灰色预测模型，并且对其扰动界进行研究。

定理5 假设原始非负序列

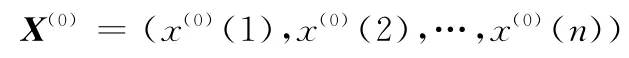
则r次反向累加生成序列为

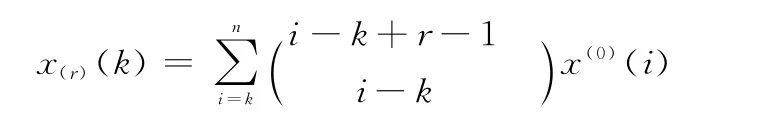
证明利用数学归纳法进行证明

当r=1时

当r=2时

假设当r=p的时，等式成立，即

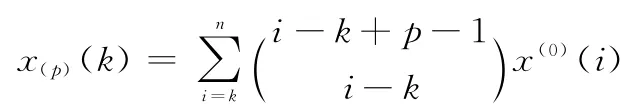
那么，当r=p+1时

综上所述，根据数学归纳法即可得到

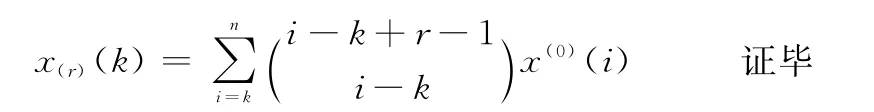
定义3 设序列X（0）、X（r）的定义同定理5，称x（r）（k+1）= β1x（r）（k）+β2（k=1，2，…，n-1）为r阶反向累加离散灰色模型。

为了分析r阶反向累加离散灰色模型的稳定性，以下分析其解的扰动情况。

定理6 假设r阶反向累加离散灰色模型的解为x，根据反向累加生成的性质和分析问题的方便，首先分析当数据序列第n项发生扰动的情况，即＾x（0）（n）=x（0）（n）+ε，因为

因为

根据定理2，可以得到

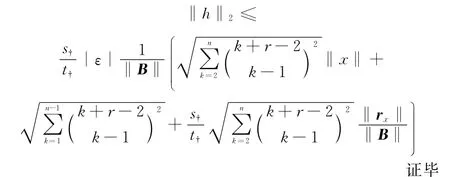
当数据序列的第n项发生扰动时，即＾x（0）（n）=x（0）（n）+ε，基于r阶反向累加的离散灰色模型的扰动界为

从上面的证明过程可以推导出，当数据序列的第t项发生扰动时，即＾x（0）（t）=x（0）（t）+ε，基于r阶反向累加的离散灰色模型的扰动界为

限于篇幅，此处不再具体证明。

从第1节的计算结果可知，基于一阶反向累加的离散灰色模型的扰动界为

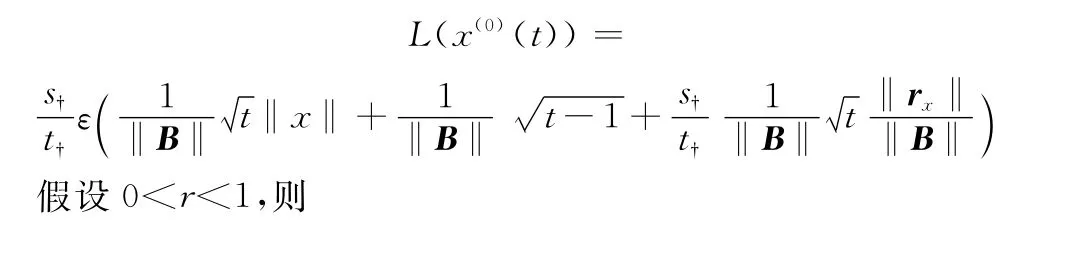
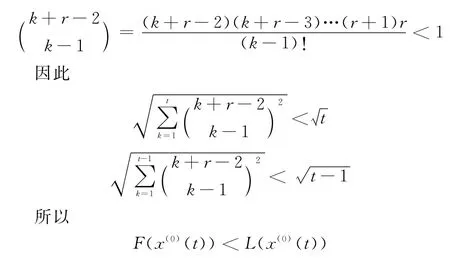
因此，当0＜r＜1时，基于r阶反向累加的离散灰色模型的扰动界要小于基于一阶反向累加的离散灰色模型的扰动界，从理论上来说，所建立的模型具有更好的稳定性。

3 算例分析

某型号的武器装备，其定期检测数据如表1所示，运用本文提出的分数阶反向累加离散灰色预测模型对系统可靠度的点估计进行预测。其中，n表示检测个数，k表示失败个数，R表示可靠度的点估计。

表1 某型号武器装备的试验信息

根据表1，可以计算得到某型号武器装备的可靠度的点估计序列为

此处可靠度的点估计为没有引入Bayes方法的计算结果。

为了和传统的灰色预测模型进行比较，本文选择了G M（1，1）模型和D G M（1，1）模型作为比较的对象，不同模型的计算结果及相对误差如表2所示，其中R D G M（1，1）表示本文提出的分数阶反向累加离散灰色预测模型，计算得到的平均绝对百分比误差（mean absolute percent error，M A PE）如表2所示。根据遗传算法求得最优阶数r=0.22，限于篇幅，具体的计算步骤不再逐步列举。

表2 不同模型的计算结果和相对误差

其中

从表2可以看出，当原始数据的第3个数据出现扰动的时候，G M（1，1）模型和D G M（1，1）模型的预测相对误差较大，而本文提出的模型，由于其扰动界较小，模型的解比较稳定，计算结果的相对误差较小，模型的模拟和预测精度较高。

4 结论

本文提出了分数阶反向累加离散灰色模型，通过数学推导，得出了模型的求解公式，求出了其扰动界，通过和一阶反向累加离散灰色模型进行比较，发现其扰动界减小，从而提高了模型解的稳定性。由于反向累加更加有效地利用了系统的新信息，所以模型的预测精度更高。最后，将分数阶反向累加离散灰色模型应用在某型号武器装备的储存可靠度的预测中，取得了很好的模拟和预测效果，为此类武器系统的维修保障提供了理论上的支持，拓展了灰色预测模型的应用领域，在理论和实际应用上都有着重要的价值。

［1］Deng J L.Control problem of grey system［J］.Systems and Control Letters，1982，1（5）：288-294.

［2］Liu S F，Lin Y.Grey systemstheory and applications［M］.Berlin：Springer-Verlag，2010：107-148.

［3］Dang Y G，Liu S F，Liu B.The G M models thatx（1）（n）be taken as initial value［J］.Chinese Journal of Management Science，2005（1）：132-134.（党耀国，刘思峰，刘斌.x（1）（n）为初始条件G M模型［J］.中国管理科学，2005（1）：132-134.）

［4］W ei Z，H e J M.Generalized G M（1，1）model and its application in forecasting of fuel production［J］.Applied Mathematical Modelling，2013，37（9）：6234-6243.

［5］Cui J，Liu S F，Zeng B，et al.Anovelgrey forecasting m odel and its optimization［J］.Applied Mathematical Modelling，2013，37（6）：4399-4406.

［6］Lin J，Lian R J.Design of a grey-prediction self-organizing fuzzy controller for active suspension systems［J］.A pplied Soft Computing，2013，13（10）：4162-4173.

［7］Li D C，Chang C J，Chen C C，et al.Forecasting short-term electricity consumption using the adaptive grey-based approach—an Asian case［J］.O mega，2012，40（6）：767-773.

［8］Samvedi A，Jain V.Agrey approach for forecasting in a supply chain during intermittent disruptions［J］.Engineering Applications of Artificial Intelligence，2013，26（3）：1044-1051.

［9］Song Z M，Deng J L.The accumulated generating operation in opposite direction and its use in grey model G O M（1，1）［J］.Systems Engineering，2001，19（1）：66-69.（宋中民，邓聚龙.反向累加生成及灰色G O M（1，1）模型［J］.系统工程，2001，19（1）：66-69.）

［10］Liu J Y，Yang T X，Wang S L.Directed method for computing parameters of G O M（1，1）［J］.Journal of Jilin University （Engineering and Technology Edition），2003，33（2）：75-79.）（刘金英，杨天行，王淑玲.反向G O M（1，1）模型参数的直接求解方法［J］.吉林大学学报（工学版），2003，33（2）：75-79.）

［11］Liu J Y，Yang T X，W ang S L.Grey opposite-direction m odelG O M（1，1）and its application［J］.Journal of Jilin A gricultural University，2002，24（4）：91-94.（刘金英，杨天行，王淑玲.反向G O M（1，1）模型及其在农药降解分析中的应用［J］.吉林农业大学学报，2002，24（4）：91-94.）

［12］Yang Z，Ren P，Dang Y G.Grey opposite-direction accu m ulated generating and optimization of G O M（1，1）model［J］.Systems Engineering-Theory&Practice，2009，29（8）：160-164.（杨知，任鹏，党耀国.反向累加生成与灰色G O M（1，1）模型的优化［J］.系统工程理论与实践，2009，29（8）：160-164.）

［13］Lian ZW，Dang Y G，Wang Z X.Properties of accumulated generating operation inopposite-direction and optimization of G O M（1，1）m odel［J］.Systems Engineering-Theory&Practice，2013，33（9）：2306-2312.（练郑伟，党耀国，王正新.反向累加生成的特性G O M（1，1）模型的优化［J］.系统工程理论与实践，2013，33（9）：2306-2312.）

［14］Xie NM，Liu S F.Discrete G M（1，1）and mechanism of grey forecasting m odel［J］.Systems Engineering-T heory&Practice，2005，25（1）：93-99.（谢乃明，刘思峰.离散G M（1，1）模型与灰色预测模型建模机理［J］.系统工程理论与实践，2005，25（1）：93-99.）

［15］Xie N M，Liu S F.Research on the affine properties of discrete grey model［J］.Control and Decision，2008，23（2）：200-203.（谢乃明，刘思峰.离散灰色模型的仿射特性研究［J］.控制与决策，2008，23（2）：200-203.）

［16］Wang F X.Discrete G O M（1，1）model and its application［J］. Journal of Xinjiang University（Natural Science Edition），2012，29（1）：75-77.（王丰效.离散G O M（1，1）模型及其应用［J］.新疆大学学报（自然科学版），2012，29（1）：75-77.）

［17］W u L F，Liu S F，Yao L G，et al.Grey system model with the fractional order accumulation［J］.Communicationsin Nonlinear Science and Numerical Simulation，2013，18（7）：1775-1785.

［18］W u L F，Liu S F，Chen D，et al.Using gray model with fractional order accu m ulation to predict gas emission［J］.Natural Hazards，2014，71（3）：2231-2236.

［19］Sun J G.M atrix disturbance analysis ［M］.Beijing：Science Press，1987：355-356.（孙继广.矩阵扰动分析［M］.北京：科学出版社，1987：355-356.）

［20］Stewart GM.O n the perturbation of pseudo-inverses，projections and linear square problems［J］.SIA M Review，1977（19）：634-662.

Fractional order reverse accumulative discrete grey model and its application

LIU Jie-fang1，2，LIU Si-feng2，W U Li-feng2，F A N G Zhi-geng2
（1.School of M athematical Science，H enan Institute of Science and Technology，Xinxiang 453003，China；2.College of Economics and M anagement，N anjing University of Aeronautics and Astronautics，N anjing 210016，China）

In order to reduce the perturbation bounds of the solution of discrete grey forecasting m odel，increase the stability ofthe solution ofthe m odel，and make full use of new information ofthe system，a fractional reverse accu m ulative discrete grey m odelis put forward.Its calculation form ula is deduced and its perturbation bounds are calculated.The specific calculation form ula is given by mathematical deduction，and the perturbation bounds are calculated.The superiority of the fractional order reverse accu m ulative discrete grey m odelis proved by co m paring the perturbation bounds ofit with the first-order reverse accu m ulative discrete grey m odel.Finally，it is applied in storage reliability prediction of a certain type of weapon system，and the calculation resultis better than the traditional grey prediction m odel.The prediction accuracy has im proved dramatically.The proposed model expands the scope of the theoretical research and practical appl ication of grey forecasting model.

grey prediction；fractional order；reverse accu m ulation；reliability

N 941.5

10.3969/j.issn.1001-506 X.2016.03.37

1001-506 X（2016）03-0719-06

2014-10-30；

2015-11-05；网络优先出版日期：2015-11-20。

网络优先出版地址：http：∥w w w.cnki.net/kcms/detail/11.2422.T N.20151120.1801.012.html

欧盟第7研究框架玛丽·居里国际人才引进计划（FP7-PIIF-G A-2013-629051）；国家自然科学基金（91324003，71171113，71271226）；国家自然科学基金与英国皇家学会国际合作交流项目（71111130211）；国家社会科学基金重点项目（12AZD102）资助课题

刘解放（1980-），男，讲师，博士，主要研究方向为灰色系统理论、复杂装备研制管理。

E-mail：liujf101@126.com

刘思峰（1955-），男，教授，博士研究生导师，主要研究方向为灰色系统理论、系统工程。

E-mail：sfliu@nuaa.edu.cn