设计参数对刚性索自锚式悬索桥受力性能的影响分析

陈淮，王艳，朱倩

(1.郑州大学 土木工程学院，河南 郑州 450001;2. 广东省冶金建筑设计研究院，广东 广州 510080)



设计参数对刚性索自锚式悬索桥受力性能的影响分析

陈淮1，王艳1，朱倩2

(1.郑州大学 土木工程学院，河南 郑州 450001;2. 广东省冶金建筑设计研究院，广东 广州 510080)

以平顶山市建设东路立交桥——刚性索自锚式悬索桥为实例，研究地锚式与自锚式悬索桥受力差异，探讨混凝土收缩、徐变对结构力学性能的影响，分析主缆矢跨比、主梁拱度、主梁抗弯刚度、主缆与吊杆的弹性模量等结构设计参数的变化对桥梁力学性能的影响规律。计算结果表明：中、小跨径刚性索自锚式悬索桥主梁轴力较地锚式悬索桥大很多，主梁的变形和其他内力差别不大；混凝土的收缩、徐变使主梁的变形和受力有较大程度的增加；设置主梁拱度和增大主缆弹性模量能有效降低主梁的内力和变形，结构刚度显著提高；增大主梁竖向抗弯刚度能有效控制桥梁变形但内力略有增加；增加吊杆弹性模量对桥梁的受力影响较小；增加矢跨比可加大桥梁竖向刚度但同时主梁轴向压力却相应减小，应综合选用。所得结论可为该类桥型设计提供参考。

刚性索自锚式悬索桥；设计参数；力学性能；有限元法

S242平顶山市建设东路立交桥位于河南省平顶山市建设东路与许南公路(G311)交叉处，跨越许南公路，属许南公路连接线的一部分，是平顶山市对外联络的咽喉，建设东路跨许南公路主线桥的主桥为跨径组合(35+72+35)m的双塔刚性索自锚式悬索桥，桥宽24.4 m，双向6车道；主梁为单箱双室钢筋混凝土箱梁，梁高1.635～1.8 m，仅在横隔板位置设置横向预应力钢绞线。主塔为钢筋混凝土实体结构，塔高13 m，在塔柱顶部设1道风撑；主缆缆索采用140根s15.2高强钢绞线，锚固在主梁两端，其中中跨主缆采用在主塔塔顶两端张拉，张拉端锚固于塔顶，边跨缆索锚固端设在主梁端部，张拉端设于塔顶，采用单端张拉，主缆外包16Mn325×12钢管，主缆张拉后钢管内真空压注50号水泥砂浆；吊杆采用12根s15.2高强钢绞线，上端(与主缆连接处)设为固定端，下端(与主梁连接处)设为张拉端，锚固端采用 P 型锚具，张拉端采用 HVM 锚具，吊杆张拉后外包16Mn194×10钢管，钢管内真空压注40号水泥砂浆，可让主缆和吊杆截面刚性化，还使内部柔性索与空气隔离，防止锈蚀，便于养护，主缆在边跨与中跨都有一段穿越主梁边腹板。桥面铺装采用80 mm厚40号钢纤维混凝土[1]。

平顶山市建设东路立交桥主桥的主缆和吊杆在施工阶段先以柔性索承受恒载，后期再用钢管将柔性索包裹，采用将吊杆与主缆在主塔两侧同时分4次交替张拉到位的张拉方案(吊杆张拉采用先张拉短吊杆后张拉长吊杆的施工顺序)[1]，通过对柔性索施加预应力，内压注浆料，形成钢管混凝土结构，使主缆和吊杆截面刚性化，加大了桥梁结构刚度，这样柔性索和钢管混凝土能够共同承受恒载和活载，解决了悬索桥在使用荷载下刚度不足的问题。该种桥型在国内外建造较少，且相关研究仅介绍了刚性索自锚式悬索桥的桥型构思、结构计算，构造措施、施工技术等[2-5]，而关于结构设计参数的变化对桥梁内力和变形影响规律的研究尚不完善。本文以平顶山市建设东路立交桥为实例，研究刚性索自锚式悬索桥设计参数变化对其受力性能的影响规律。

1　桥梁有限元模型

采用有限元程序Midas/civil建立该桥的空间有限元计算模型，各主要受力构件的模拟为：主塔、塔间风撑选用空间梁单元模拟，主梁选用空间“脊骨梁”单元模拟，主缆与吊杆选用杆梁复合单元模拟：以桁架单元(杆单元，下同)模拟内部的柔性索，在桁架单元节点上并行建立梁单元模拟外部钢管混凝土结构，来反映其刚性的受力特点；主梁与吊杆之间采用刚臂连接，在程序中通过弹性连接中的刚性连接来实现；主缆与吊杆的初张力通过对桁架单元施加初拉力的方法来实现；主缆自重刚度的影响通过在桁架单元的弹性刚度矩阵中增加初应力刚度矩阵来实现。桥梁计算模型边界条件的约束方式：塔梁固结；左右桥塔的塔底边界模拟，以左塔外侧塔底为基准，分别沿桥梁纵向和横向采用一端铰支、另一端滑动铰支座处理；边跨端部支座节点按双向滑动铰支座处理。

2　结构设计参数变化对桥梁力学性能的影响分析

2.1自锚式悬索桥和地锚式悬索桥结构受力对比分析

由于自锚式悬索桥的主缆直接锚固在加劲梁的两端，加劲梁直接承受由主缆锚固端传来的水平压力和竖向剪力的作用，结构受力比较复杂，为了对比分析自锚式悬索桥和地锚式悬索桥在受力性能上的差异，在所建立的刚性索自锚式悬索桥计算模型的基础上，将主缆与主梁端部的连接约束释放，直接将主缆端节点约束，其他计算参数不变，从而建立刚性索地锚式悬索桥计算模型。桥梁的恒载由程序自动加载，桥梁所承受的活载按公路Ⅱ级车道荷载确定，全桥对称布置，计算主梁的挠度、弯矩和轴力[6]，限于篇幅，把中跨跨中和变化率最大位置处的计算结果见表1。

表1地锚式悬索桥与自锚式悬索桥模型计算结果比较

Table 1 Compare toself-anchored suspension bridge and earth-anchored suspension’s results

主梁内力与变形位置自锚式模型地锚式模型变化率/%挠度/m中跨L/8-6.40×10-3-6.08×10-3-0.51中跨跨中-3.82×10-2-3.80×10-2-0.51弯矩/(N·m)中跨L/84.50×1063.96×106-11.99中跨跨中2.59×1072.53×107-2.23轴力/N边跨端-2.77×107-1.22×104>1000中跨跨中-2.66×107-2.04×10692.33

注：变化率=(地锚式悬索桥计算结果-自锚式悬索桥计算结果)/自锚式悬索桥计算结果×100%

分析计算结果可知：刚性索自锚式悬索桥主梁的挠度、弯矩及轴力较刚性索地锚式悬索桥大，其中轴力增大约1个数量级以上，计算结果符合物理概念；挠度和弯矩差别不大，变化率最大值约在12%以内，且由于该刚性索自锚式悬索桥的主缆在中跨位置穿越主梁腹板，主梁的变形牵连主缆及桥塔结构，致使主梁挠度和弯矩变化率最大值没有发生在跨中，而是在中跨L/8和7L/8附近，且向边跨端部和中跨跨中呈现逐渐减小趋势。

2.2混凝土收缩徐变的影响

混凝土的收缩、徐变会引起吊杆、主缆及主梁内力的重分布，特别是自锚式悬索桥主梁在巨大的轴向压力作用下，这种因素影响更为显著，为分析混凝土收缩、徐变给结构带来的影响，分别建立考虑和不考虑混凝土收缩、徐变2种刚性索自锚式悬索桥计算模型，其他计算参数不变，活载加载方式与第2.1节相同，计算得出主梁的挠度及弯矩[6]，中跨跨中和变化率最大位置处的计算结果如表2所示。

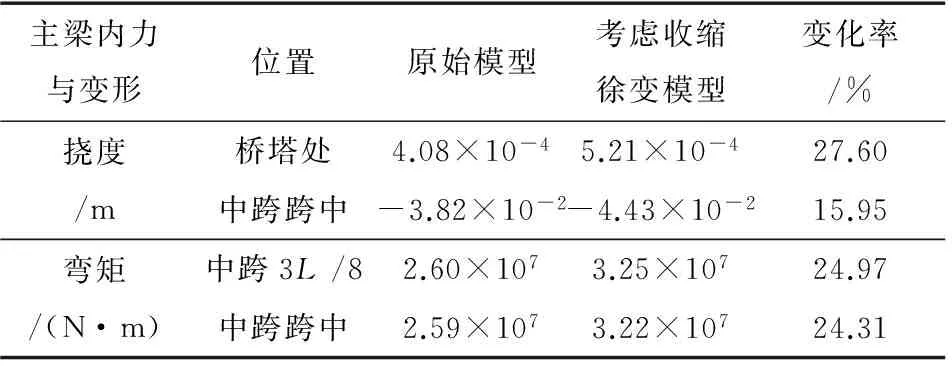
表2　混凝土收缩、徐变的影响

注：变化率=(收缩徐变模型结果-原始模型结果)/原始模型结果×100%

由计算结果可知，考虑混凝土收缩、徐变后，主梁的挠度及弯矩有一定程度增大，且在桥塔处附近挠度增加变化率最大，为28.74%，然后变化率依次向边跨及中跨跨中逐渐降低；弯矩在中跨3L/8处增加最多，变化率最大值为26.34%。说明混凝土的收缩、徐变对桥梁的受力影响较大，在设计时应注意这一特点。

2.3主梁拱度对桥梁结构受力的影响

建设东路立交桥主梁设置了拱度，跨中比端部高0.841 m，由于加劲梁中有巨大的轴向力，设置加劲梁拱度将会影响主梁在荷载作用下的受力。为分析主梁拱度的对结构受力的影响，分别建立主梁水平的计算模型和考虑主梁拱度的计算模型，其他计算参数不变，活载加载方式与第2.1节相同，通过计算得出主梁挠度与弯矩[6]，中跨跨中和变化率最大位置处的计算结果如表3所示。

表3主梁拱度对主梁变形与内力的影响

Table 3 Effect of girder’s camber to main girder’s displacement and internal force

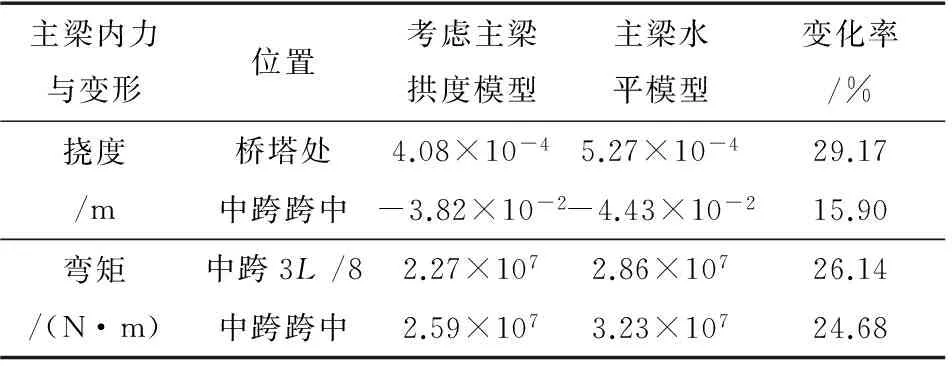
主梁内力与变形位置考虑主梁拱度模型主梁水平模型变化率/%挠度/m桥塔处4.08×10-45.27×10-429.17中跨跨中-3.82×10-2-4.43×10-215.90弯矩/(N·m)中跨3L/82.27×1072.86×10726.14中跨跨中2.59×1073.23×10724.68

注：变化率=(主梁水平模型结果-主梁拱度模型结果)/主梁拱度模型结果×100%

对比计算结果可以得出：主梁拱度对主梁的受力和挠度影响较大，设置主梁拱度后，主梁的挠度和弯矩均有较大幅度的降低，其中挠度降低变化率最大值在桥塔位置附件，为29.17%，变化率依次向边跨及跨中逐渐降低；弯矩降低程度较均匀，分布在18.72%～26.14%范围内，变化率最大发生在中跨跨中处。由此可知，设置主梁拱度能够有效降低主梁的内力和变形，与文献[7]所得柔性索自锚式悬索桥结论一致。

2.4矢跨比对桥梁结构受力的影响

悬索桥主跨的矢跨比决定着主缆的线形及水平拉力，矢跨比的改变必将引起悬索桥结构体系的受力变化，为探讨矢跨比对刚性索自锚式悬索桥受力性能的影响，分别建立从1/5～1/8范围内若干个不同矢跨比的桥梁计算模型，不改变计算模型中的其他因素，只改变桥梁的矢跨比，活载加载方式与第2.1节相同，计算得出桥梁主梁挠度、弯矩、轴力与矢跨比的关系如图1所示。

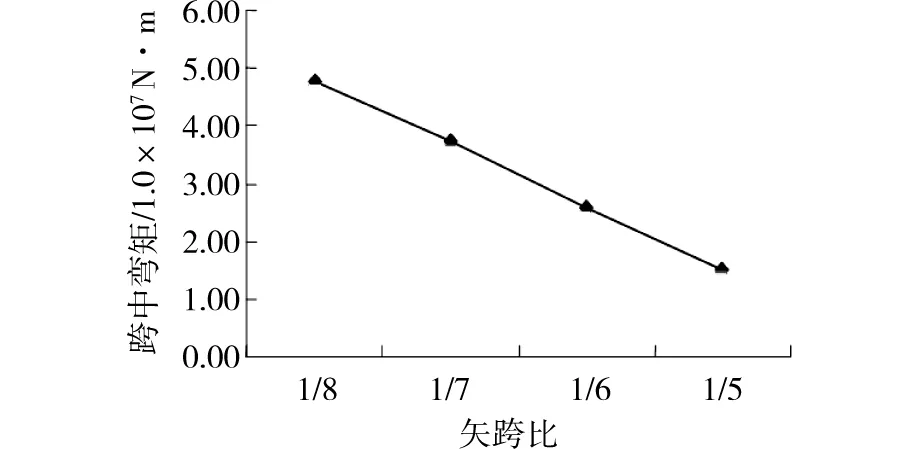
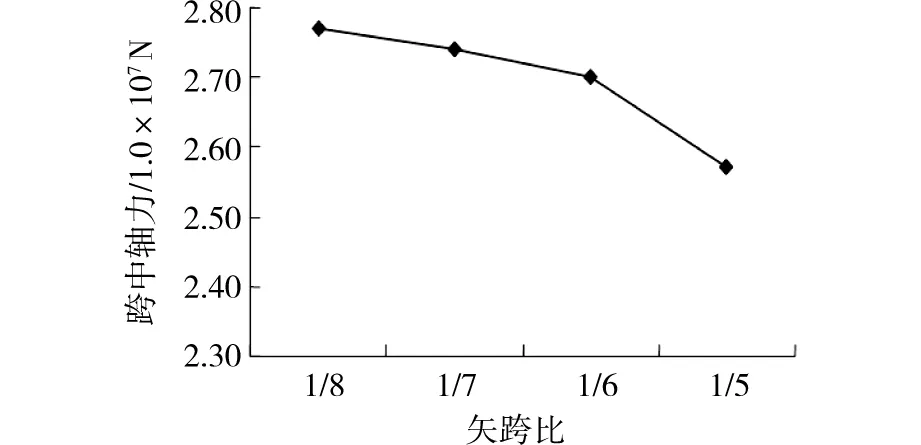
图1　主梁跨中挠度、内力与矢跨比的关系Fig.1 Relationship of main girder’s deflection, internal force and cable’s ratio of rise to span

分析计算结果可知，随着矢跨比的增加，主梁的挠度和弯矩相应减小，说明矢跨比的增加可使桥梁竖向刚度增大；但同时主梁的轴向压力却相应降低。矢跨比增加还需增加桥塔的高度和索的长度，且靠近主缆位置由于坡度较大，不利于施工及主缆的维护[8]。因此，若想充分利用主梁轴向压力来减小主梁尺寸及节省预应力筋配置的数量，则应当在桥梁设计时综合考虑主梁内力、结构尺寸、刚度、施工和维护等影响因素，进行优化比选，选择出经济、合理的矢跨比。目前建造的自锚式悬索桥一般采用较大的矢跨比，矢跨比大多集中在1/6左右[9-10]。

2.5主梁抗弯刚度对桥梁结构受力的影响

加劲梁竖向抗弯刚度不仅影响到结构内力的分配，而且对主梁截面形式的选择和桥梁整体受力性能均有影响。通过从6～20 m4变化主梁的竖向抗弯惯性矩，分别建立若干个计算模型，其他计算参数不变，活载加载方式与第2.1节相同，探讨主梁竖向抗弯刚度变化对结构受力的影响。计算结果如图2所示。

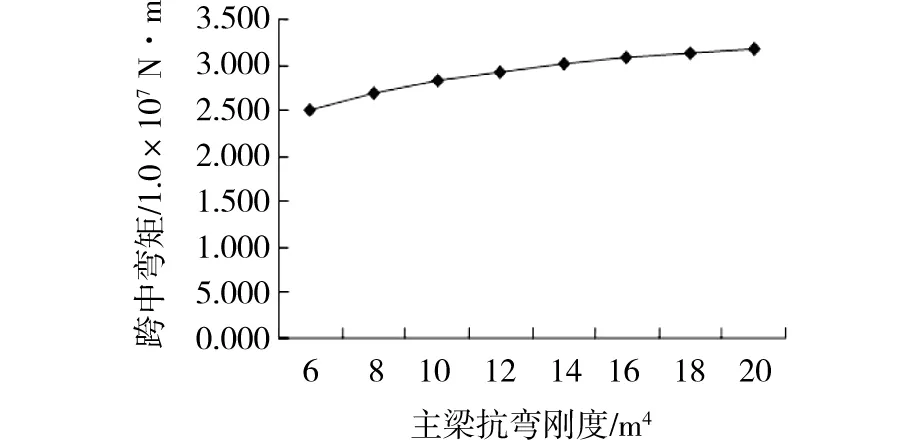
图2　主梁跨中挠度、弯矩与主梁抗弯刚度的关系Fig.2 Relationship of main girder’s deflection, bending moment and flexural rigidity

由图2可知，随着主梁竖向抗弯刚度的增大，主梁跨中挠度逐渐降低，而主梁跨中弯矩略有增大，说明增大主梁的竖向抗弯刚度虽然能够有效控制主梁的挠度，减小主梁变形，但根据刚度分配原则，主梁分配到的内力也在增大，因此，在桥梁设计中如采用增加主梁竖向抗弯刚度控制主梁变形时需综合考虑主梁内力和截面应力变化，不能为了减小主梁跨中挠度而盲目增大主梁的抗弯惯性矩，通过综合考虑选用合适的主梁尺寸。

2.6主缆弹性模量对桥梁结构受力的影响

分别建立若干个不同主缆弹性模量的计算模型，弹性模量从0.8×105MPa变化到2.2×105MPa，其他计算参数不变，活载加载方式与第2.1节相同，分析主缆弹性模量的变化对桥梁结构受力性能的影响。计算结果如图3所示。

分析上述结果得出，随着主缆弹性模量的增大，主梁跨中挠度和弯矩随之减少，且幅度较大，结构刚度有效提高。这是由于主缆弹性模量的增大意味着主缆抗拉刚度的增加，根据刚度分配原则，主缆分担荷载的比例加大，相应主梁分配荷载的比例减少，故主梁内力与变形减少。所以在进行自锚式悬索桥设计时可以考虑选用弹性模量大的主缆材料来降低主梁跨中挠度和弯矩，提高结构竖向刚度。

图3　主梁跨中挠度和弯矩与主缆弹性模量的关系Fig.3 Relationship of main girder’s deflection, bending moment and main girder’s modulus of elasticity

2.7吊杆弹性模量对桥梁结构受力的影响

为研究吊杆弹性模量变化对结构受力性能的影响，分别建立不同吊杆弹性模量的计算模型，其它计算参数不变，活载加载方式与第2.1节相同，计算结果如图4所示。

图4　主梁跨中挠度、弯矩与吊杆弹性模量的关系Fig.4 Relationship of main girder’s deflection, bending moment and suspender’s modulus of elasticity

随着吊杆弹性模量的增加，主梁跨中挠度和弯矩有所减小，但幅度较小，说明吊杆作为主缆与主梁之间的传力构件，其弹性模量(抗拉刚度)的增加只能使主梁与主缆之间的相对变形降低，而对整个桥梁结构的受力和变形影响较小，应根据实际情况考虑经济性和实用性来选择合适的吊杆材料。

3　结论

1)中、小跨径刚性索自锚式悬索桥的主梁轴力较刚性索地锚式悬索桥会增大1个数量级以上；主梁的变形和其他内力差别不大。

2)混凝土的收缩、徐变对中、小跨径刚性索自锚式悬索桥的受力影响较大，使主梁的变形和受力增加。

3)设置主梁拱度和增大主缆弹性模量均能有效降低主梁的内力和变形，结构竖向刚度显著提高。

4)增加矢跨比可加大桥梁结构竖向刚度，但主梁轴向压力却相应减小，加大矢跨比还需增加桥塔的高度和索的长度。中、小跨径刚性索自锚式悬索桥设计应综合考虑主梁内力、结构尺寸、竖向刚度、施工和维护等因素的影响，选择经济、合理的矢跨比。

5)增大主梁的竖向抗弯刚度能够有效降低主梁的挠度，但主梁分配到的内力也增大，采用增加主梁竖向抗弯刚度控制主梁变形时需考虑主梁内力及截面应力的变化，综合选用合适的主梁尺寸。

6)增加吊杆弹性模量只能使主梁与主缆之间的相对变形降低，而对整个中、小跨径刚性索自锚式悬索桥的结构受力和变形影响较小。

[1] 冯广胜．自锚式悬索桥技术问题探讨[J]．公路，2006(5)：86-89．

FENG Guangsheng. Discussion about technical problems of self-anchored suspension bridge[J]. Highway, 2006(5): 86-89.

[2] 林长川，李映，凌建中．刚性索悬索桥[J]．公路，2000，(9)：41-45．

LIN Changchuan, LI Ying, LING Jianzhong. Rigid cable suspension bridge[J]. Highway, 2000, (9):41-45.

[3] 李映，林长川．刚性索悬索桥研究[J]．重庆交通学院学报，2001，20(1)：10-14．

LI Ying, LIN Changchuan. Research of rigid cable suspension bridge[J]. Journal of Chongqing Jiaotong University, 2001, 20(1):10-14.

[4] 李映．常州广化桥设计[J]．桥梁建设，2002(5)：43-45．

LI Ying. Design of Guanghua bridge in Changzhou[J]. Bridge Construction, 2002(5):43-45.

[5] 张元凯，肖汝诚，金成棣．自锚式悬索桥的设计[J]．桥梁建设，2002(5)：30-32．

ZHANG Yuankai, XIAO Rucheng, JIN Chengdi. Design of self-anchored suspension bridge[J]. Bridge Construction, 2002(5):30-32.

[6] 朱倩．刚性索自锚式悬索桥力学性能分析[D]．郑州：郑州大学，2006．

ZHU Qian. Mechanical properties analysis of rigid self anchored suspension bridge[D]. Zhengzhou: Zhengzhou University, 2006.

[7] 石磊，张哲，刘春城，等．混凝土自锚式悬索桥设计及其力学性能分析[J]．大连理工大学学报，2003，43(2)：202-206．

SHI Lei, ZHANG Zhe, LIU Chuncheng, et al. Design and mechanical performance analyses of concrete self-anchored suspension bridge[J]. Journal of Dalian University of Technology, 2003, 43(2): 202-206.

[8] 和秀岭．自锚式悬索桥结构参数变化对结构静力特性的影响[J]．公路交通科技(应用技术版)，2009，5(11)：159-160，164．

HE Xiuling. The affection of static properties on design parameters change of self-anchored suspension bridge[J]. Journal of Highway and Transportation Research and Development(Application Technology), 2009,5 (11): 59-160,164.

[9] 程伟,石坚,朱凌志.自锚式与地锚式悬索桥结构设计参数对比研究[J].上海公路,2010(3):64-57,67.

CHENG Wei, SHI Jian, ZHU Lingzhi. Contrastive analysis of design parameters between self-anchored and earth anchored suspension bridge [J]. Shanghai Highways,2010(3):64-57,67.

[10] 王志诚，刘昌鹏，沈锐利．自锚式悬索桥参数影响挠度理论研究[J]．土木工程学报，2008，41(12)：61-65．

WANG Zhicheng, LIU Changpeng, SHEN Ruili. Parametric effects on self-anchored suspension bridges using deflection theory[J]. China Civil Engineering Journal, 2008, 41(12):61-65.

Impact analysis on mechanical behavior design parameters ofself-anchored suspension bridge with rigid cable

CHEN Huai1，WANG Yan1,ZHU Qian2

(1. School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China；2.Guangdong Metallurgical Architectural Design & Research Institute，Guangzhou 510080，China)

Taking the overpass of Pingdingshan Jianshe road, which is a self-anchored suspension bridge with rigid cable, as an example, this paper investigated the effect of mechanical behavior of concrete shrinkage creep on the structural mechanics performance. Meanwhile, the influences of span ratio of the main cable, camber, flexural rigidity of main girder and the modulus of elasticity of cable and suspender were discussed. The results show: the main girder’s axial force of medium and small span self-anchored suspension bridge with rigid cable is greater than that of earth-anchored suspension. There are little differences between the main girder’s displacement and internal force. The theory of elasticity may be adopted to analyze self-anchored suspension bridge with rigid cable. Main girder’s displacement and internal force can be enhanced because of the concrete shrinkage creep. Setting up the main girder’s camber and amplifying the cable’s modulus of elasticity can availably reduce the main girder’s displacement and internal force, the structural stiffness can be obviously improved as well. The bridge’s displacement can be availably controlled by increasing the vertical deflection resistance stiffness, but the internal force can be slightly enlarged. The increase of the suspender's modulus has a little effect on bridge's force. The increase of cable's ratio of rise to span may improve bridge’s vertical deflection resistance stiffness and at same time reduce main girder’s axial force, thus it should be synthetically utilized. The conclusions can be consulted for similar bridges.

self-anchored suspension bridge with rigid cable, design parameters, mechanical property, finite element method

2015-10-15

河南省杰出人才计划项目(084200510003)

陈淮(1962-)，男，河南淮阳人，教授，博士，从事桥梁结构理论与工程应用研究；E-mail：chen0418@126.com

U448.25

A

1672-7029(2016)08-1563-06