扁平箱梁气动特性CFD模拟的维数对比研究

祝志文，袁涛，陈魏

(湖南大学 土木工程学院，湖南 长沙 410082)



扁平箱梁气动特性CFD模拟的维数对比研究

祝志文，袁涛，陈魏

(湖南大学 土木工程学院，湖南 长沙 410082)

基于三维非定常雷诺时均Navier-Stokes (RANS)方程和SST k-ω湍流模型，数值模拟雷诺数为1.06×105时扁平箱梁气动特性在不同主梁展向长度、不同展向网格分辨率下的气动特性，确定三维CFD模拟合理的主梁展向参数，获得主梁气动力系数和漩涡脱落St数随来流攻角的变化。对相同箱梁开展了不同攻角下二维RANS计算，并将二维和三维主梁的整体气动特性、表面压力分布进行对比。研究结果表明：三维RANS获得的主梁气动特性结果与计算域展向网格分辨率和主梁长度均无关；二维和三维模拟结果非常一致，均能获得箱梁气动力系数平均值的合理估计，因而工程计算可采用二维模拟。开展的节段模型风洞试验表明二维和三维模拟得到的漩涡脱落St数是合理的，典型攻角下扁平箱梁裸梁具有单一St数，且均明显大于成桥状态。

扁平箱梁；气动特性； RANS；二维和三维模拟

湍流是一种极其复杂的流动形式。为获得对湍流流动的描述，雷诺在1886年就提出了用时间平均值的概念来研究湍流流动。他认为湍流中的所有物理量虽然都随时间和空间变化，但任意瞬时的运动仍然符合连续介质流动的特征，流场中任一空间点也应适用流体运动的基本方程。且由于各个物理量都具有某种统计学特征，所以控制方程中任一瞬时的物理量都可用其平均量和脉动量之和来代替，因而可对整个Navier-Stokes方程进行时间平均运算。

对不可压流动，任一瞬时的流动物理量可表示为：

(1)

(2)

(3)

其中：t和x分别为时间和空间坐标；ρ和υ分别为空气密度和运动黏性。

动量方程可进一步写成

(4)

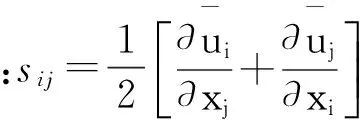
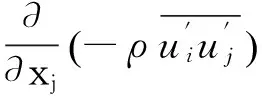
风工程中几乎所有流动问题，由于流动雷诺数高，其绕流流动均是复杂的湍流流动。因而目前风工程数值模拟需要借助湍流模型来获得流场描述、风荷载大小和加载特征。又由于风工程中的绕流物体往往具有钝化的气动外形和尖锐的棱角，流动总是出现强烈的分离、物面再附、再分离、漩涡脱落和复杂的尾流流动。因此所采用的湍流模型应能处理高应变率及大弯曲程度的流动，能模拟逆压和分离流动，具有较强的捕捉流动各向异性的能力。本文采用SSTk-ω湍流模型研究桥梁断面的气动特性，并依此开展二维和三维模拟的比较。

1　湍流模型方程

如果采用涡黏模型封闭上述方程, 对应的雷诺应力可表示为,

(5)

Menter提出了一种SST(ShearStressTransport)k-ω模型[2]。该模型通过对SSTk-ω模型方程和标准k-ε模型方程分别乘以混合函数Fl和(1-Fl)。通过设定近壁区内Fl取值1，使得近壁区的流动采用SSTk-ω模型模拟；在近壁区以外Fl为0，从而过度到标准k-ε模型。其中标准k-ε模型方程为[3]

(6)

(7)

其中:σk和σε分别是k和ε的湍流普朗特数；Cε1和Cε2为常数。标准k-ε模型是一种高雷诺数湍流模型，适合于充分发展的湍流，但在湍流边界层内紧靠壁面区的黏性子区内，流动雷诺数低，并不是充分发展的湍流，需要使用如下的低雷诺数k-ω湍流模型[4]：

(8)

(9)

这样， SST k-ω湍流模型结合了标准k-ε模型和k-ω湍流模型各自的优缺点，通过不同湍流模型用于不同的流动区域计算，能获得优于标准k-ε模型和SSTk-ω模型的模拟结果[5]。

2　研究对象

以丹麦大带东桥主跨加劲梁为研究对象。该桥为主跨1 624 m的双塔三跨连续钢箱梁悬索桥，加劲梁横断面为扁平闭口六边形，桥面布置如图1所示。该加劲梁全宽B=31 m，桥轴线处梁高4.4 m。该桥在设计阶段开展了大量的风洞试验[6]。为与风洞试验对比，CFD模拟采用与节段模型风洞实验一致的缩尺比和来流风速[6]，对应的流动Re=1.06×105。由于作者无法获得桥梁栏杆、导流板和检修道等附属设施的详细结构设计细节，本文CFD计算不考虑桥面栏杆和其他附属设施，相当于加劲梁的施工状态。

图1　加劲梁横断面布置Fig.1 Layout of girder cross section

3　数值方法实现

二维和三维CFD模拟均采用1:80的模型缩尺比，绕加劲梁横断面的计算域如图2所示。计算域的入口、上侧和下侧边界到加劲梁断面中心的距离均为13B，对应的模型堵塞度为0.5%，显著小于风工程对模型堵塞度不大于3%的要求[7]。下游出口到加劲梁扭转中心(Shear center，S.C.)的距离为26B，目的是减小下游边界对模型区流动的影响。采用计算域分区划分网格以控制网格的正交性和相邻网格边长比不大于1.2，计算域分区网格划分见文献[8]。由于前后缘尖角小半径圆化对主梁气动特性没有影响[8]，为减少高Re数下的计算域网格总数，提高主梁前后缘网格正交性，前后缘圆化半径均为0.25 mm，如图3所示。经计算结果的网格无关检查，确定二维主梁物面第一条网格到物面的最大距离为2.9×10-5B，计算Re数下的最大Y+为0.43，以度量网格正交性的等角斜度(Equiangle skew)QEAS参数最大值为0.4，保证了较好的网格正交性。二维计算域网格总数为55 332，其他详细信息见文献[8]。对展向不同主梁长度、不同网格分辨率的三维计算模型，其任意主梁横截面的网格划分和参数与二维网格完全相同，如图4所示。

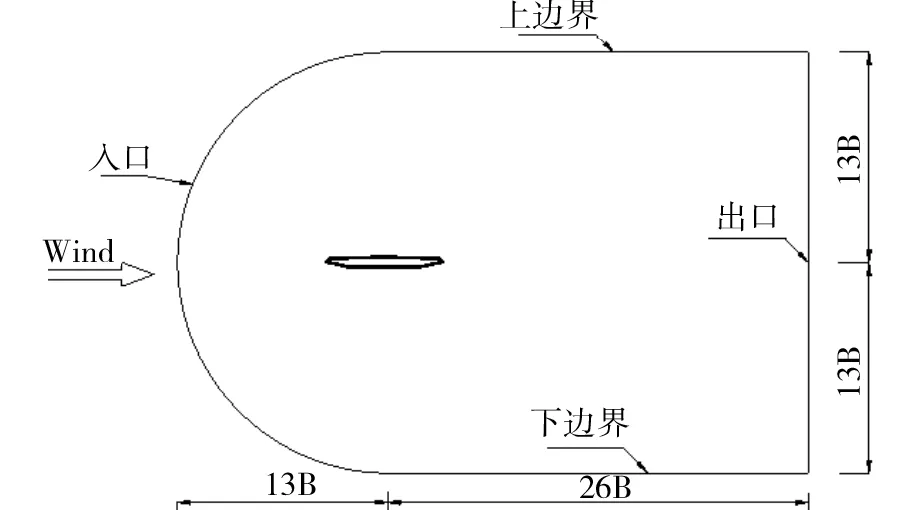
图2　加劲梁与计算域Fig.2 Schematic plot of computational domain around girder

计算域边界条件为：计算域入口为水平层流速度边界，下游出口施加牛曼边界条件；加劲梁表面为无滑移壁面条件；计算域上、下边界采用对称边界条件，三维主梁的2个端截面所在边界同样采用对称边界条件。计算域初始场采用入口速度条件初始化。数值计算采用循序渐进的推进策略，以平抑初始场计算导致的数值振荡和数值发散，缩短计算时间。最终的CFD计算控制方程时间离散采用非定常二阶隐式格式，采用速度-压力解耦的SIMPLE算法，压力方程采用二阶格式离散，对流项、湍动能方程和湍流耗散率方程均采用QUICK格式。经二维计算的时间步无关检查，确定的无量纲时间步长Δ=0.003 1，并用于三维CFD计算。通过监视气动力时程，当加劲梁上作用的气动力收敛后开始保存每步上的气动力和压力数据，所有数值模拟均基于CFD专用程序Fluent 6.3开展。

图3　加劲梁前缘网格Fig.3 Grids around girder leading edge

图4　三维计算域主梁横断面网格Fig.4 Mesh slice at girder cross section in three-dimensional domain

4　数值模拟结果和讨论

4.1计算结果的处理和监测

定义加劲梁断面气动升力、阻力和扭矩系数分别为：

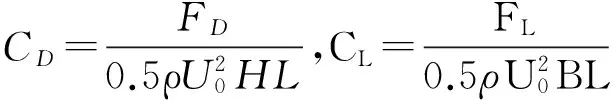
(10)

其中:U0为计算域入口风速,FL，FD和M分别为作用在加劲梁上的阻力(顺来流方向为正)、升力(垂直来流方向向上为正)和扭矩(逆时针方向为正)；H和L分别为加劲梁断面高度和模拟的加劲梁展向长度，二维时L为单位长度。

定义加劲梁漩涡脱落St数：

St=fsH/U0

(11)

式中:fs为加劲梁漩涡脱落频率,Hz。

为获得主梁表面的压力分布特征，本文分别在二维主梁截面和三维主梁展向中截面上相同位置布设了160个监测点。压力监测点的分布疏密根据表面压力梯度的大小调整，在前后缘点位置加密，如图5所示。定义测点的压力系数为

(11)

其中:P为监测点静压；Pr为参考点压力，参考点均设在计算域入口边界。

4.2二维CFD模拟结果

二维模拟的来流攻角范围为-6～+6，得到的气动力系数如图6所示。可见在模拟的攻角范围内，阻力系数0°攻角最小，偏离0°攻角均逐渐增大；升力系数随攻角的增大而增大，扭矩系数随攻角的增大而减小。另外，0°攻角下的阻力系数和升力系数，均与不带栏杆截面二维模拟采用RNGk-ε模型和雷偌应力模型(RMS)接近[9]。风洞试验阻力系数明显偏大，其原因是栏杆和附属设施明显增大了截面阻力[6]。且。图7是St数随来流攻角的变化，其值在0.27～0.28，表现为对来流攻角变化不敏感。图8是0°攻角下主梁三分力系数时程，可见计算结果已充分收敛，力系数时程已非常平稳。虽然时程脉动量非常小，但仍然可基于升力时程的涡脱频率(图9)获得涡脱St数的估计值。

图5　主梁断面压力监测点布置Fig.5 Arrangement of pressure monitoring point on girder surface

图6　三分力系数随来流攻角的变化Fig.6 Force coefficients vs. wind angle of attack

图7　主梁St数随来流攻角的变化Fig.7 Girder St number vs. wind angle of attack

图8　主梁三分力系数时程Fig.8 Force coefficients records of girder

图10是0°攻角下主梁表面平均压力系数分布(曲线与物面间画填充线的为负压，后同)。可见除前缘上下腹板上部分区域为正风压外，主梁表面其它区域均为负风压，在顶底板最上游侧的棱角，负压峰值很大。最大正风压系数0.95位于前缘点下，最大负风压系数-1.94位于顶板最上游点，下游表面的风压系数一般在-0.3～-0.2范围，主梁大部分区域风压系数绝对值较小。

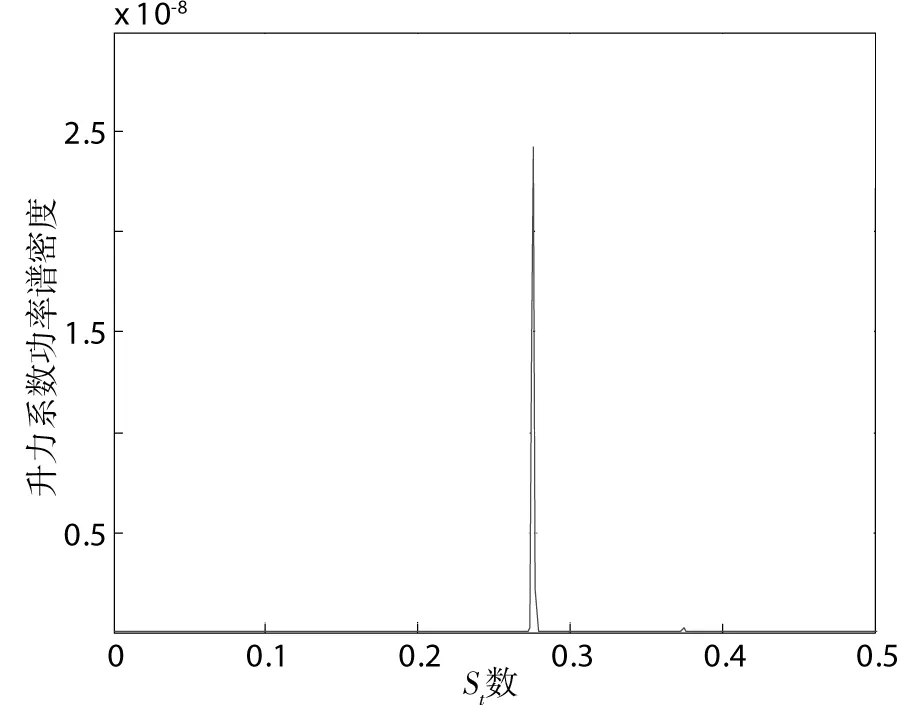
图9　升力系数时程功率谱分析Fig.9 PSD plot of lift coefficient records

图10　主梁表面平均压力系数分布Fig.10 Pressure coefficients distribution on girder surface

4.3三维CFD模拟结果

对桥梁主梁的三维CFD模拟，需要研究主梁展向网格分辨率和主梁展向长度对其气动特性的影响，由此确定主梁气动特性模拟的合理展向长度和网格分辨率。

4.3.1主梁展向网格分辨率对气动特性计算结果的影响

针对主梁展向长度为1倍主梁宽度的情况，计算了0° 攻角下5种不同主梁网格分辨率，如表1所示。对不同主梁展向网格分辨率，在垂直主梁轴向的平面，网格划分与二维模拟完全相同。主梁气动力系数和涡脱St数见表2，同时列出了二维RANS的相应参数值。

表1显示5种不同网格分辨率的气动三分力系数完全相同，而St数差别也非常小。这说明，采用三维RANS模拟主梁气动特性与计算域展向网格分辨率无关。同时，0° 攻角下三维计算结果与二维结果非常接近，偏差最大的为阻力系数，而相对误差仅为3.9%。

表1不同展向网格分辨率的流动结果

Table 1 Flow results of girder under various spanwise grid resolution

模型编号展向网格数量CDCLCMStR-1100.30790.0437-0.0330.281R-2200.30790.0437-0.0330.283R-3300.30790.0498-0.0330.280R-4400.30790.0498-0.0330.277R-5600.30790.0498-0.0330.279二维模拟0.31990.0464-0.0330.279

4.3.2裸梁St数的节段模型风洞试验

为验证本文CFD模拟获得的St合理性，在湖南大学HD-2风洞中开展了大带东桥节段模型风洞试验。节段模型几何缩尺比为1∶60，模型截面宽B=51.67 cm，高D=7.34 cm，模型总长250 cm，模型为不带栏杆和附属设施的裸梁。模型直立在风洞内，在节段模型的正下游1.5B，离风洞底板0.6 m高度处布设Cobra-100风速仪，如图11所示。通过测量模型尾迹纵向脉动风速，由频谱分析来估算模型的漩涡脱落频率和St数。FFT分析点数为1 024，采用分段平均周期图法估计功率谱。

图11　节段模型试验Fig.11 Sectional model wind tunnel test

图12是试验来流风速分别为5和8 m/s，裸梁在3种典型攻角下尾迹风速测量得到的涡脱St数，约为0.27～0.29。这说明典型攻角下大带桥裸梁具有单一St数，其值为0.28～0.29，均明显大于成桥状态，因此施工阶段大跨度桥梁可能会呈现明显不同于成桥状态的涡振特性。

(a)5 m/s;(b)8 m/s图12　裸梁基于尾迹风速测量的涡脱St数Fig.12 Vortex shedding St number of bare deck based on wind speed measured in wake

4.3.3主梁展向长度对气动特性计算结果的影响

三维CFD模拟需检查不同主梁展向长度对气动参数的影响。基于主梁气动特性不受计算域展向网格分辨率影响的结论，下面针对计算域展向30个网格的模型，分别模拟计算域5种不同主梁展向长度，得到的气动参数见表2。

从表2可见，采用不同的主梁展向长度，其气动三分力系数和漩涡脱落St数几乎完全一致，且与二维结果非常接近，最大偏差为阻力系数，但其相对误差仅为3.9%。可见，三维RANS模拟的气动特性结果，不受主梁展向长度的影响。

因三维RANS模拟的主梁气动特性，与计算域展向网格分辨率和主梁展向长度均无关，因而三维RANS模拟可采用更为简化的CFD网格模型。本文确定采用展向1倍主梁宽度和展向10个均匀网格划分的R-1计算模型，据此研究在不同来流攻角下的主梁气动特性。

表2展向不同长度主梁的流动结果

Table 2 Flow results of girder under various spanwise girder length

模型编号展向长度/BCDCLCMStL-10.50.30790.0497-0.03260.281L-210.30790.0498-0.03260.280L-31.50.30790.0497-0.03260.280L-420.30790.0496-0.03260.282L-530.30790.0497-0.03260.281二维模拟0.31990.0464-0.0330.279

4.3.4不同攻角下主梁气动特性

三维计算的来流攻角范围为-6～+6，得到的气动力系数和漩涡脱落St数见图6～7。可见三维结果与二维结果具有完全相同的趋势，且同一攻角下的结果差别非常小。最大偏差为阻力系数，但相对差别仅为4%左右。St数取值同样在0.28～0.29左右，且表现为对来流攻角变化不敏感。图13是0°攻角下三维主梁轴向中截面表面平均压力系数分布。与图10相比，平均压力分布的特征是完全相似的，顶底板最上游侧的棱角负压峰值均很大，但最小负压系数值-2.11小于二维情况，且已改变到位于下底板最上游棱角处。图14是6°攻角下三维主梁的三分力系数时程，可见力系数计算结果已收敛，但与图7相比由于攻角增大，力系数平均值均已增大，且波动幅度也增大。

风洞试验给出了来流风速和纵向湍流度分别为12 m/s和7.5%，该加劲梁成桥状态0°攻角的阻力、升力和扭矩系数分别为0.57，0.067和0.028[6]。由于本文来流为均匀流，且风洞试验模型包含桥面栏杆、防撞墙和检修道等桥面附属设施，因而本文结果与风洞试验结果没有严格的可比性。当防撞栏等桥面附属设施引入后，主梁气动外形将明显钝化，小攻角时其阻力系数可能会增大60%～100%左右，这样本文二维和三维的阻力系数值将比较接近风洞试验结果。另外，该桥实桥发生涡振的St数约为0.1～0.14，显著低于本文计算结果。其中原因尚不清，可能的原因包括防撞栏等桥面附属设施引入后，主梁气动外形将明显钝化，其涡脱特征可能明显改变；且由于RANS模型只能获得非定常流动的时均结果，而漩涡脱落是桥梁绕流流动分离、再附、在分离和剪切流融合的强烈非定常运动，二维和三维RANS模型可能无法获得漩涡脱落St数的合理估计。

图13　主梁中截面平均压力系数分布Fig.13 Pressure coefficients distribution on girder span central section

图14　6°攻角主梁力系数时程Fig.14 Force coefficients records of girder under 6° angle of attack

图15为来流攻角为6°时，绕三维箱梁中截面的流线，可见绕箱梁的流动比较平顺，在箱梁后缘存在由于流动分流形成的回流区和上下表面分流剪切流的融合，这些特征同样可在来流攻角为6°时的二维模拟中见到，如图16所示。

图15　6°攻角绕三维箱梁中截面的流线Fig.15 Streamlines around three-dimensional girder at span central section under 6° angle of attack

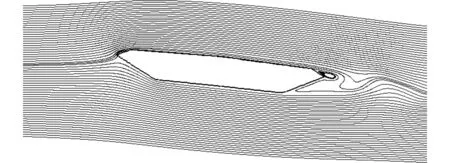
图16　6°攻角绕二维箱梁的流线Fig.16 Streamlines around two-dimensional girder under 6° angle of attack

5　结论

1)基于二维和三维模拟RANS模拟，获得箱梁气动力系数平均值的合理估计。

2)节段模型风洞试验和二维、三维模拟得到的漩涡脱落St数是一致的，典型攻角下扁平箱梁裸梁具有单一St数，且均明显大于成桥状态。

3)三维RANS计算的主梁气动特性结果，与计算域展向网格分辨率和主梁展向长度均无关，因而三维RANS模拟可采用更为简化的CFD模型。

4)二维和三维模拟获得的箱梁气动特性差别很小，从工程应用的精度要求和研究周期，扁平闭口箱梁可仅开展二维CFD模拟，有三维外形特征的主梁除外(如含展向变化的桥面附属设施)。

[1] Tannehill J C, Anderson D A, Pletcher R H. Computational fluid mechanics and heat transfer[M]. 2nd edition. Taylor & Francis, Washington, D.C., 1997: 165-176.

[2] Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32: 269-289.

[3] Jones W P, Launder B E. The prediction of laminarization with a two-equation model of turbulence[J]. International Journal of Heat and Mass Transfer, 1972, 15: 301-314.

[4] Wilcox D C. Re-assessment of the scale-determining equation for advanced turbulence models[J]. AIAA Journal, 1988, 26: 1414-1421.

[5] 祝志文,夏昌.基于两种湍流模型的桥梁颤振导数识别研究及比较[J].湖南大学学报(自然科学版),2010, 37(11)：6-11.

ZHU Zhiwen, XIA Chang. Comparative study of two turbulence models based on the identification of flutter Derivatives of Bridges[J]. Journal of Hunan University (Natural Sciences), 2010, 37(11): 6-11.

[6] Larsen A. Aerodynamic aspects of the final design of the 1624m suspension bridge across the Great Belt[J]. J Wind Eng Ind Aerodyn, 1993, 48: 261-285.

[7] Tominagaa Y, Mochidab A, Yoshiec R, et al. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 1749-1761.

[8] 祝志文.均匀流中箱梁非定常风压的频域特征和空间相关性[J].中国公路学报，2014,27(6):68-76.

ZHU Zhiwen. Frequency-domain characteristics and spatial coherence of unsteady wind pressure on box girder surface in smooth flow[J]. China Journal of Highway and Transport，2014,27(6):68-76.

[9] Bruno L. The validity of 2D numerical simulations of vortical structures around a bridge deck[J]. Mathematical and Computer Modelling, 2003,37(3):795-828.

Comparative investigation on prediction of aerodynamic characteristics of steel flat box girders by CFD with different simulation dimension

ZHU Zhiwen, YUAN Tao, CHEN Wei

(School of Civil Engineering, Hunan University, Changsha 410082, China)

Based on three-dimensional unsteady Reynolds averaged Navier-Stokes (RANS) equations and the SST k-ω turbulent model, the aerodynamic characteristics of a flat box girders under various spanwise length and grid resolution were numerically computed at the Reynolds number of 1.06×105. According to the determined optimal spanwise parameters in CFD, the aerodynamic force coefficients and vortex-shedding Strouhal number were obtained under different wind angles of attack. Flow results of the girder under the same condition were also simulated on the basis of the two-dimensional RANS equations, its aerodynamic forces and pressure on girder surface were compared to the three-dimensional modeling. It is found that the results obtained from three-dimensional simulations is independent on grid resolution and girder length in spanwise direction, and agree well with the results from two-dimensional simulations. Both the two- and three-dimensional RANS modeling can present reasonable estimation on mean aerodynamic coefficients of the girder. Therefore, the two-dimensional modeling is feasible for bridge engineering application. The wind tunnel tests provided confirmed that the estimated vortex-shedding Strouhal number from two- and three-dimensional RANS modeling, and under typical wind angle of attack(-3°～+3°), the bare deck presents only one Stnumber, which is significantly larger than that of girder in service.Key words：box girder; aerodynamics; RANS; two- and three-dimensional modelling

2015-10-14

国家重点基础研究发展计划(973计划)项目(2015CB057701，2015CB057702)；国家自然科学基金资助项目(51278191)；湖南省交通科技资助项目(201522)

祝志文(1968—)，男，教授，博士，从事大跨度桥梁和结构抗风、钢桥疲劳与断裂、桥梁冲刷等研究；E-mail: zwzhu@hnu.edu.cn

TU328

A

1672-7029(2016)08-1555-08