CENTRAL LIMIT THEOREM AND CONVERGENCE RATES FOR A SUPERCRITICAL BRANCHING PROCESS WITH IMMIGRATION IN A RANDOM ENVIRONMENT*

Yingqiu LI (李应求)

Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering，School of Mathematics and Statistics，Changsha University of Science and Technology，Changsha 410004，China

E-mail:liyq-2001@163.com

Xulan HUANG (黄绪兰) Zhaohui PENG (彭朝晖)

School of Mathematics and Statistics，Changsha University of Science and Technology，Changsha 410004，China

E-mail:1764955427@qq.com;2634931960@qq.com

Abstract We are interested in the convergence rates of the submartingale to its limit W，where (Πn) is the usually used norming sequence and (Zn) is a supercritical branching process with immigration (Yn) in a stationary and ergodic environment ξ.Under suitable conditions，we establish the following central limit theorems and results about the rates of convergence in probability or in law:(i) W-Wn with suitable normalization converges to the normal law N (0，1)，and similar results also hold for Wn+k-Wn for each fixed k∈N*;(ii) for a branching process with immigration in a finite state random environment，if W1 has a finite exponential moment，then so does W，and the decay rate of P (|W-Wn|＞ε) is supergeometric;(iii) there are normalizing constants an(ξ)(that we calculate explicitly) such that an(ξ)(W-Wn) converges in law to a mixture of the Gaussian law.

Key words Branching process with immigration;random environment;convergence rates;central limit theorem;convergence in law;convergence in probability

1 Introduction

A branching process with immigration in a random environment is a natural and important generalization of the Galton-Waston process.Kesten，Kozlov and Spitzer[1]gave limit laws for a random walk in a random environment by using a branching process in an independent and identically distributed (i.i.d.) random environment with one immigrant at each generation.Bansaye[2]studied a model of cell contamination by investigating a branching process in a random environment with immigration.For a supercritical branching process with immigration in a random environment，Wang and Liu[3]considered theLpconvergence aboutWn，a central limit theorem，and large and moderate deviation principles about logZn.Li and Huang[4]studied the a.s.convergence rate for the submartingale associated with a branching process with immigration in a random and varying environment.For a subcritical multitype branching process with immigration in an ergodic and stationary random environment，Key[5]found that under suitable conditions，the process converges to a proper limit law.Roitershtein[6]considered a central limit theorem and a strong law of large numbers for the partial sum of the process.Vatutin[7]used a multitype branching process with immigration that evolves in a random environment to research polling systems with random regimes of service.

The objective of this paper is to extend the theorems of Wang，Gao and Liu[8]and Huang and Liu[9]to a branching process with immigration in a random environment.To this end，we need to overcome some significant difficulties in the proof.For example，the usual decompositionfor a branching process is no longer valid in the immigration case.Furthermore，for the convergence rate in probability，we need to have careful control of the Laplace transforms.For the convergence rate in law，since the probability ofZn→∞orZn→0 is no longer equal to 1 in immigration case，we cannot use the method in[9].

We now explain brie fly the organization of this paper.In Section 2，we give some results about the central limit theorem and the convergence rates for a branching process with immigration in a random environment.In Sections 3-5，we prove Theorem 2.1 in Section 3，Theorem 2.2 in Section 4 and Theorem 2.3 in Section 5.

2 Branching Process With Immigration in a Random Environment

In general，we write N={0，1，2，...}，N*={1，2，...}and R for the set of real numbers.Letξ=(ξ0，ξ1，ξ2，...) be an ergodic and stationary sequence of random variables.This sequence represents the environment.Assume that each realization ofξncorresponds to two probability distributions on N:one is the offspring distribution denoted by

and the other is the distribution of the number of immigrants denoted by

A branching process (Zn)n≥0with immigration (Yn)n≥0in the random environmentξcan be defined as follows:

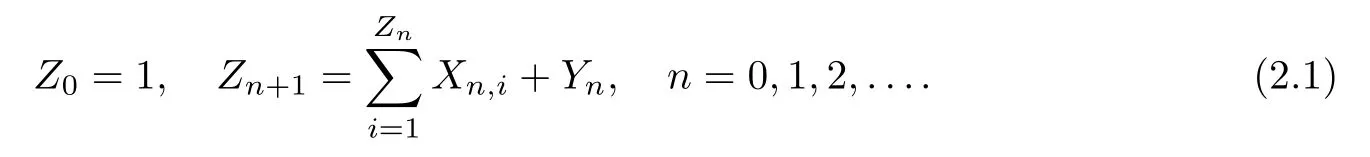
Here，given the environmentξ，the random variablesXn，i(n≥0，i≥1) andYn(n≥0) are all independent of each other，andXn，i(i=1，2，...) andYnhave the distributionp(ξn) and(ξn)，respectively.For simplicity，we writeX0=X0，1(whose distribution isp(ξ0) conditional on the environmentξ).

Let (Γ，Pξ) be the probability space under which the process is defined when the environmentξis given.The total probability P is usually called the annealed law.The quenched law Pξmay be considered to be the conditional probability of the annealed law P givenξ.LetY=(Y0，Y1，...) and Pξ，Ybe the conditional probability of P givenξandY.The expectation with respect to Pξ，Y(resp.Pξ，P) will be denoted by Eξ，Y(resp.Eξ，E).

Forξ=(ξ0，ξ1，...)，n≥0 andp＞0，we can define

By convention，for a random variableX，when we write EX，we suppose implicitly that the expectation EXis well-defined，but the value of this may probably be in finite.Thenmn(p)=

whenr＞n;we write

As in[3]，to include the immigrants in the family tree，we add one particle at each timen;thus we call the eternal particle，and we denoted it by 00，01，02，...with 0n:=0n-10(the juxtaposition of 00withntimes 0)，considering that theYnimmigrants are direct children of 0n.To form a tree we also consider that each 0n+1is a direct child of 0n.Thus all particles of a branching process with immigration in a random environment are composed of two disjoint trees:one begins with the initial particle Ø and includes all its descendants，the other begins with the eternal particle 00and all its descendants (including all the immigrants).We denote by，respectively，the number of particles in thengeneration for the two disjoint trees.We see that () is a branching process in a random environment，and that

In this article，we always assume that

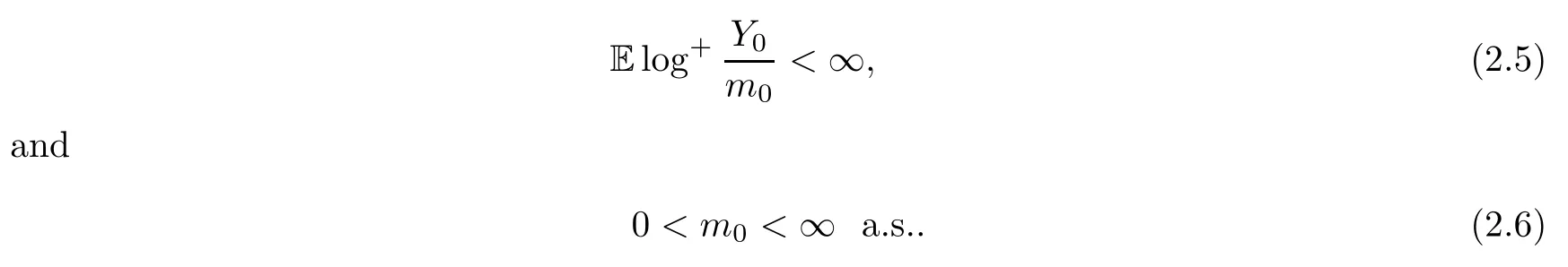
The normalized population sizeis a nonnegative martingale with respect to the filtration Fn，and the limit

exists a.s.with Eξ≤1.By (2.3)，the process is supercritical (cf.Athreya and Karlin[10]).By (2.3) and (2.4)，E=1.By Theorem 3.2 in[3]and (2.5)，we know that (Wn) is a submartingale with respect to the filtration (Fn)，and that the limit

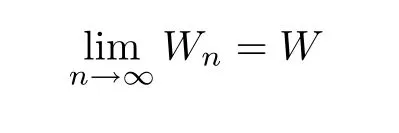
exists a.s..

In general，we writeTnξ=(ξn，ξn+1，...) ifξ=(ξ0，ξ1，...) andn≥0.

From Lemma 3.2 in[8]，we set

We first consider the central limit theorems onW-WnandWn+k-Wnfor fixedk≥1 with an appropriate normalization.

Theorem 2.1Assume that (2.3) and (2.4) hold，thatexist，thatm0(2)＜∞a.s.and that

In the case wherek=∞，suppose，additionally，that Elog＜∞.We write

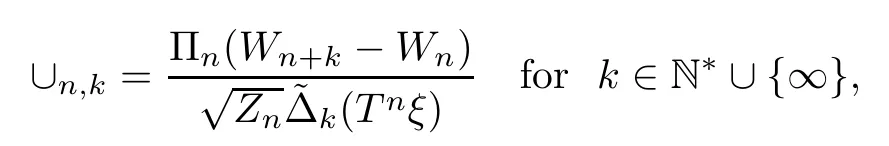
where，by convention，Wn+k=Wifk=∞.Then，for eachk∈N*∪{∞}，asn→∞，

For eachk∈N∪{∞}，we believe that

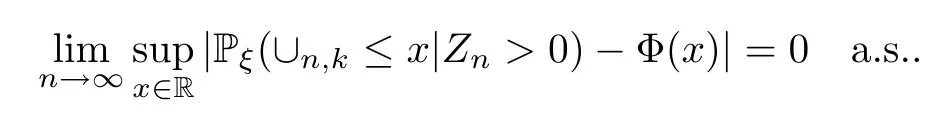
We notice that in the branching process without immigration in a random environment，(2.10) reduces to the results of Wang，Gao and Liu[8].

We next show a super-geometric convergence rate in probability for a branching process with immigration in a finite state random environment under an exponential moment condition.

Theorem 2.2For a branching process with immigration in a finite state random environment withp0(ξ0)=0，p1(ξ0)＜1 a.s.and (2.8).We have that

(a) EeθW＜∞for someθ＞0 if and only if Eeθ0W1＜∞for someθ0＞0;

(b) if Eeθ0W1＜∞for some constantθ0＞0，and there existθ2＞1 so that Eξeθ2Yn+j-1is uniformly bounded，then there exist constantsC＞0 andγ＞0 such that

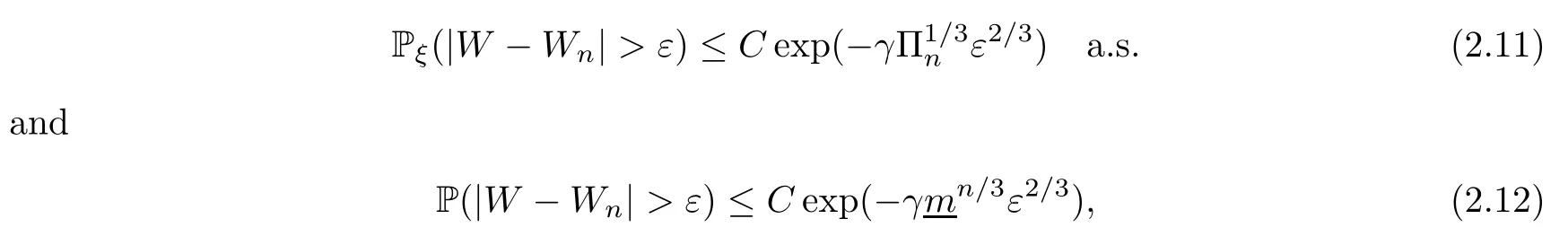
where:=essinfm0＞1.

We finally show that under a second moment condition，with an appropriate normalization，W-Wnconverges in law to a non-trivial distribution.

Theorem 2.3Suppose thatpi(ξ0)＜1 a.s.for alli∈N.Forx∈R，set Φ1(x)=，whereGis a Gaussian random variable with distributionN(0，1)，independent ofWunder Pξ.Assume that (2.8) holds，thatandexist，and that＜∞.Then

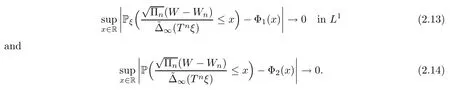
As a matter of fact，(2.13) is a quenched version of a convergence result in law:it says that the quenched law of

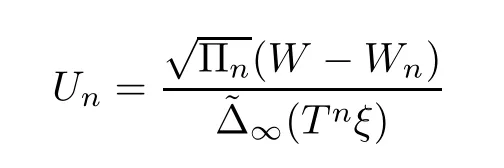
converges in some sense to a non-degenerate distribution.(2.14) is an annealed version of convergence in law，stating that the annealed law ofUnconverges to a non-degenerate distribution.

If we replace ΠnwithZnand Φi(i=1，2) within (2.13) and (2.14)，we get the central limit theorem (i.e.Theorem 2.1)，which is a generalization of Hedye (1971，[11]) and Heyde and Brown (1971，[12]) on the Galton-Watson process，and Wang，Gao and Liu (2011，[8]) for a branching process in a random environment.Compared with Theorem 2.1，the advantage of Theorem 2.3 is that the norming factor only depends on the environment.

3 Proof of Theorem 2.1

We start by demonstrating a central limit theorem under a second moment condition;this plays a key role in the proof of Theorem 2.1.This result is given as Lemma 3.2，and that proof depends on the decomposition ofW-Wnshown by Lemma 3.1.In Lemma 3.1，we decomposeW-Wnin terms of(n，i) and(0n+j-1i).In general，forx＞0，we write log-x=max{-logx，0}for the negative part of logx.

Lemma 3.1For allk＞0，the decomposition formula

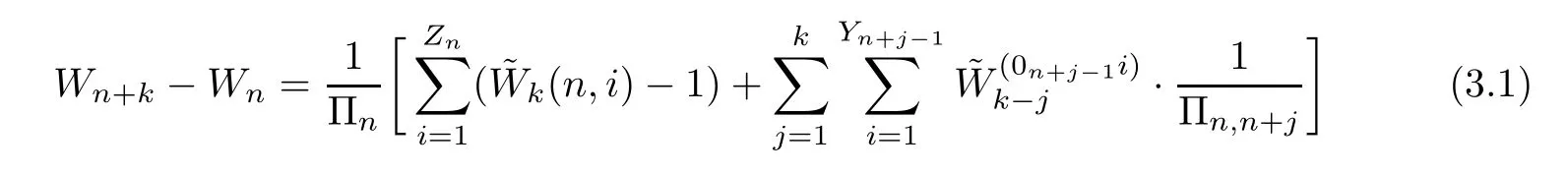
forWn+k-Wnholds a.s..Furthermore，if (2.4)，(2.5) and (2.6) hold，and

then we have the following decomposition ofW-Wnin terms of:

ProofBy definition，

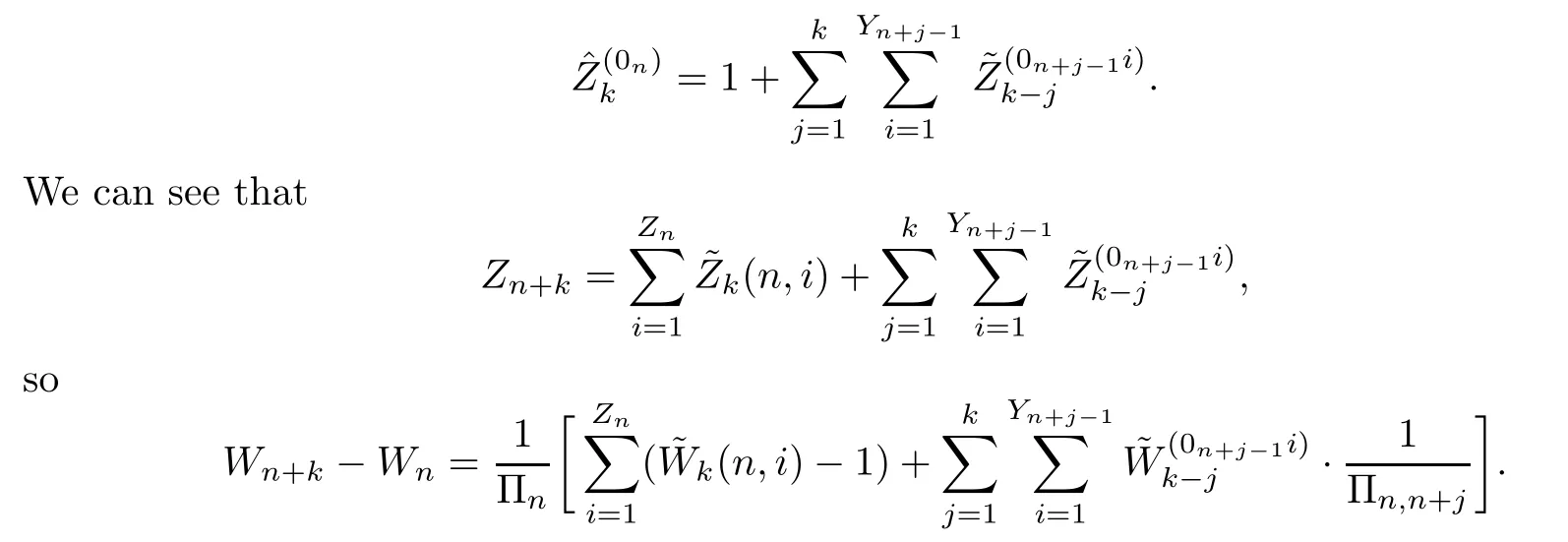
From (3.1) and the dominated convergence theorem (applied to the functionsdk(j)=defined on N*equipped with the counting measure)，using Theorem 3.2 in[3]and the fact that

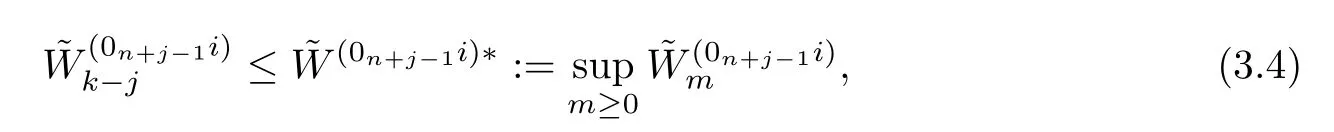
we can see that (3.3) holds，provided that

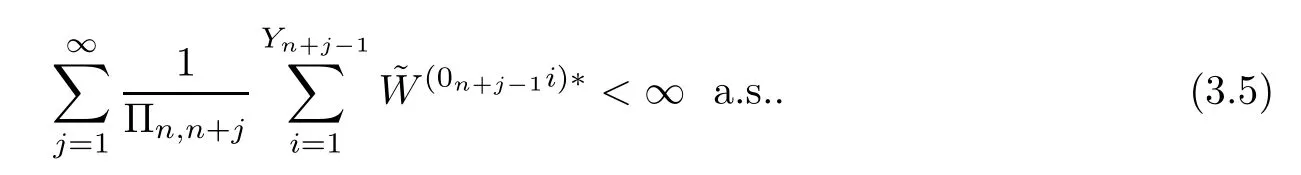
We notice that under the quenched law Pξ，all the random variables～W(n，i)(i≥1)，Yn+j-1(j≥1) andare independent of each other.Taking our expectation with respect to Pξ，Y，we know that (3.5) is implied by

By Theorem 1.3 in[13]or Theorem 3 in[14]，E (log-m0)2＜∞implies that E～W(001)*＜∞.□

By (3.1)，we can see that

Lemma 3.2Assume that the assumptions of Theorem 2.1 hold.Setrn∈N withrn→∞.Fork∈N*∪{∞}，we can define

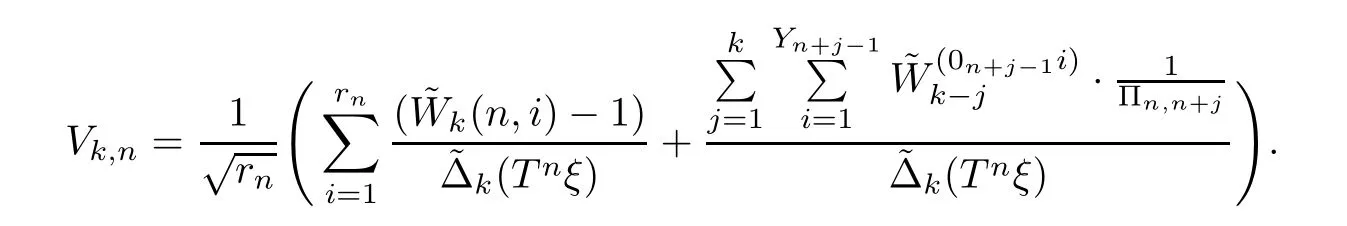
Fixk∈N*∪{∞}.Then，for each subsequence{n′}of N withn′→∞，there is a subsequence{n′′}of{n′}withn′′→∞such that，for a.e.ξand allx∈R，asn′′→∞，

ProofLet

First，we prove that there is a subsequence{n′′}，such that Pξ(Bk，n′′≤x)→Φ(x) for a.e.ξand allx∈R asn′′→∞.Fixk∈N*∪{∞}.In order to use Lindeberg’s theorem，forn∈N andε＞0，we consider the quantity

where for a setA，we write Eξ(X;A) for Eξ(X1A)，with 1Adenoting the indicator function ofA.For allε＞0，asn→∞，

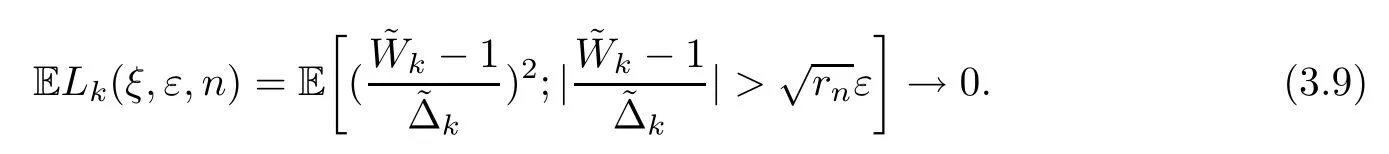
Let{n′}be a subsequence of N.From (3.9)，we choose a subsequence{n′′}for whichLk(ξ，ε，n′′)→0 a.s.，but this sequence may depend onε.We shall use a diagonal argument to select a subsequence{n′′}of{n′}，whenn′′→∞，so for allε＞0，Lk(ξ，ε，n′′)→0 a.s..Let

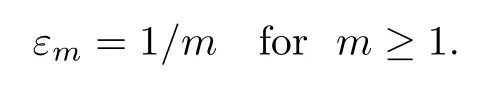
Set{n0，i}={n′}.Due to (3.9)，there is a subsequence{n1，i}of{n0，i}and a set Λ1withτ(Λ1)=1 such that∀ξ∈Λ1，

Inductively，form≥1，when Λmand{nm，i}are defined such thatτ(Λm)=1 and∀ξ∈Λm，Lk(ξ，εm，nm，i)→0，and there is a subsequence{nm+1，i}⊂{nm，i}and a set Λm+1withτ(Λm+1)=1 such that∀ξ∈Λm+1，

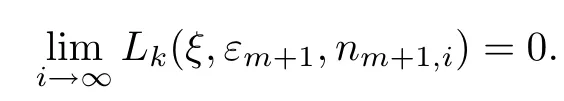
Now，we consider the diagonal sequence{ni，i}i≥1andFor each fixedε＞0，setm≥.Thenεm≤ε，and by the monotonicity ofLk(ξ，ε，n) inε，we can see that∀ξ∈Λ，

As{ni，i}is a subsequence of{nm，i}wheneveri＞m，this implies that

Sinceτ(Λ)=1，we have shown that for allε＞0，(3.10) holds a.s..It follows that a.s.(3.10) holds for all rationalε＞0，and therefore for all realε＞0，by the monotonicity ofLk(ξ，ε，ni，i) inε.Therefore，according to Lindeberg’s theorem，it is a.s.that for allx∈R，asi→∞，

Thus the lemma has been proven with{n′′}={ni，i}.

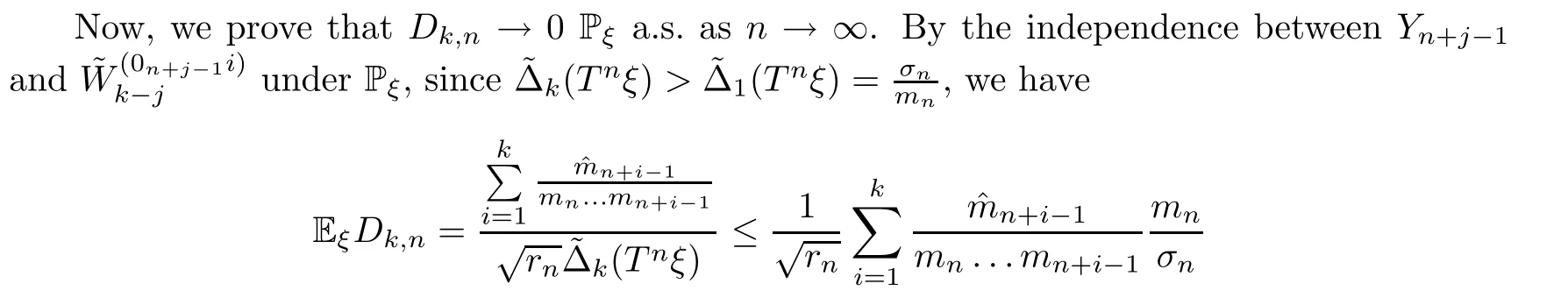
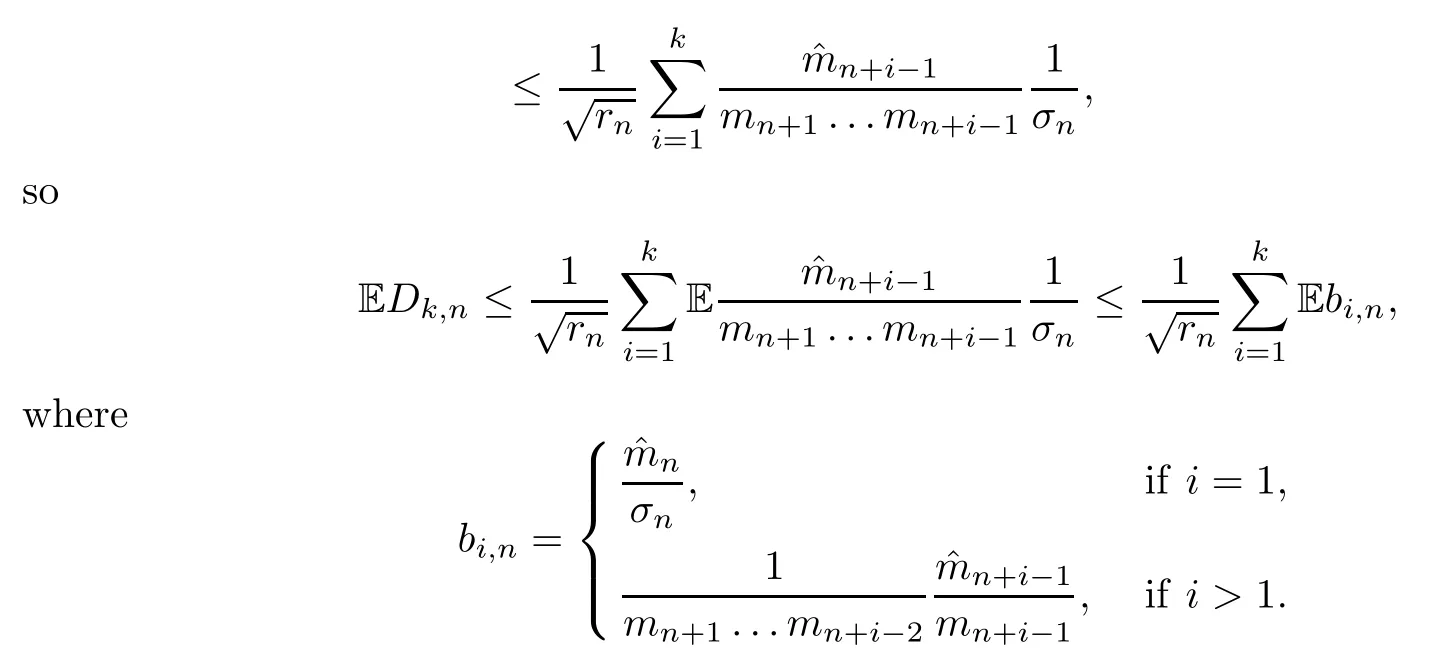
Taking the expectation，we have

and we know thatDk，n′′→0 Pξa.s.，thatBk，n′′converges toN(0，1) in law under Pξ，by Slutsky’s theorem (see Loeve[16])，and thatVk，n′′converges toN(0，1) in law under Pξ.Therefore，we can see that

Proof of Theorem 2.1We will only deal with the case wherek=∞，as the case wherek∈N*can be treated similarly.First，we prove the following assertion:for each subsequence{n′}of N withn′→∞，there exists a subsequence{n′′}of{n′}withn′′→∞such that，for a.e.ξand allx，asn′′→∞，

By (3.3)，

To show the main idea，let us consider the case whereq(ξ)=0 a.s.;i.e.，for a.e.ξ，

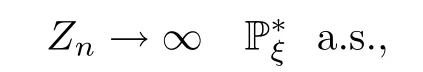
In this case，(3.12) becomes

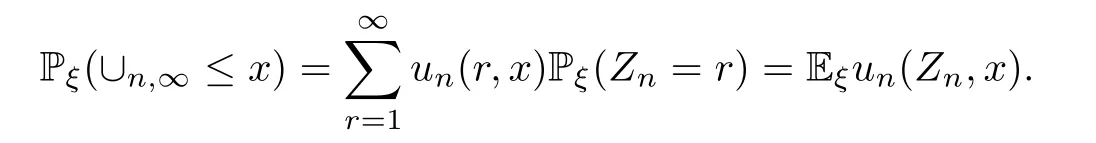
By Lemma 3.2，for each subsequence{n′}of N withn′→∞，there exists a subsequence{n′′}of{n′}withn′′→∞such that，for a.e.ξand allx，asn′′→∞，

According to the dominated convergence theorem，for a.e.ξand allx，asn′′→∞，

Thus we have proven (3.11).

Since Pξ(∪n′′，∞≤x|Zn′′＞0) are distribution functions and Φ(x) is a continuous distribution function，by Dini’s Theorem (Theorem 1.11 in[17])，we can see that，for a.e.ξ，asn′′→∞，

According to the dominated convergence theorem，(3.13) implies that，asn′′→∞，

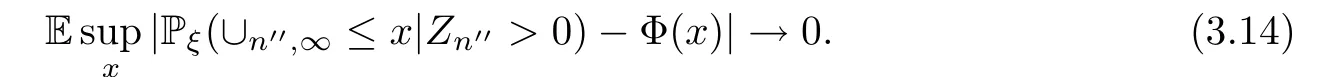
Thus we have proved that for each subsequence{n′}of N withn′→∞，there is a subsequence{n′′}of{n′}withn′′→∞such that (3.14) holds.Thus This gives (2.9) fork=∞.The proof fork∈N*is similar.

Now，we begin to prove (2.10).We have proven that for each subsequence{n′}of N there is a subsequence{n′′}since that (3.13) holds，which implies that for allx∈R and a.e.ξ，asn′′→∞，

It follows that，for allx∈R and a.e.ξ，

so by the dominated convergence theorem，we can see that for eachx∈R，asn′′→∞，

According to Dini’s Theorem，it follows that

Thus we proven that for each subsequence{n′}of N，there is a subsequence{n′′}of{n′}withn′′→∞such that (3.15) holds.Hence

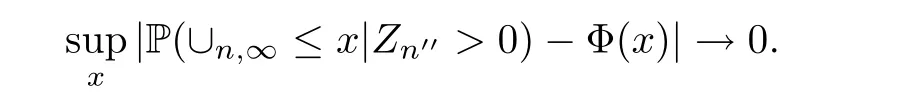
This completes the proof. □

4 Proof of Theorem 2.2

In this section，we deal with a branching process (Zn) with immigration in a finite state random environment，where eachξntakes values in a finite set{a1，a2，...，aN}.Before the proof of Theorem 2.2，we first give four lemmas.

The first lemma is an elementary result of the Laplace transform.

Lemma 4.1([9]，Lemma 5.1) LetXbe a random variable with EX=0.Assume that Eeδ|X|≤Kfor some constantsδ＞0 andK＞0.Thenwhere

The second lemma is a generalization of a result of Huang and Liu (2014，[9]，Lemma 5.2) on the branching process in a random environment about the exponential conditional moments ofWn.By (2.8) and the ergodic theorem，there exists a constantC1such that

Lemma 4.2Let (Zn) be a branching process with immigration in a finite state random environment withm0＞1 a.s..Assume that (2.8) holds and that Eξeθ0W1≤Ka.s.for some constantsθ0＞0 andK＞0.Then there exists constantsθ1＞0，C2＞0 andC3＞0，such that

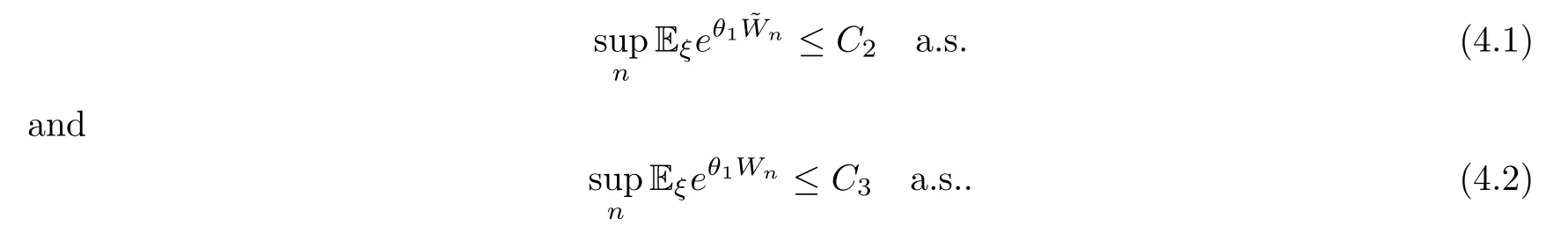
ProofFrom Lemma 5.2 in[9]，there exist constantsθ1＞0 andC2＞0 such that supna.s..Ifξ0takes values in a finite set{a1，a2，...，aN}，denote

Lemma 4.3LetX≥0 be a positive random variable such that Eet0X≤Cfor some constantst0，C＞0.Then，for each 0＜t1＜t0，there is a constantC4depending only ont0-t1such that

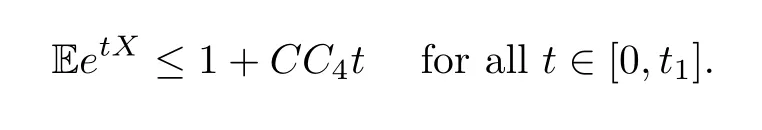
ProofUsing the mean value theorem for the functionh(t)=EetXand the fact thatx≤C4e(t0-t1) xfor some constantC4depending only on (t0-t1) and allx＞0，we obtain，for allt∈(0，t1]，that

This gives the desired inequality. □

The following lemma is a more general result than Theorem 2.2 about the supergeometric convergence rate of Pξ(|W-Wn|＞ε)，where we do not suppose that the environment has finite state space:

Lemma 4.4Assume that (2.8) holds and thata＞m0＞1，and thatp0(ξ0)=0 a.s..If supnand supnEξeθ1Wn≤C3a.s.for some constantsθ1＞0，C2＞0 andC3＞0，and there existθ2＞1 such that Eξeθ2Yn+j-1is uniformly bounded，then there exist constantsC＞0 andγ＞0 such that

ProofSetting，we haveφξ(θ)＜∞for 0＜θ≤θ1.Denote

Under Pξ，random variables{(n，i)}iare independent of each other and independent of Fn，and have the common conditional distribution

First，we prove thatfξ(θ，k)≤C5.We have，for 0＜θ≤min{θ1，1}，

for 0＜θ＜min{，1}，it follows that

Next，we prove thatgξ(θ，k)≤C6.By Lemma 4.3，the independence betweenandYn+j-1under Pξ，and the fact that the Laplace transforms ofandYn+j-1are uniformly bounded，we have，for

Next，by (3.3)，(4.4) and (4.5)，for，we see that

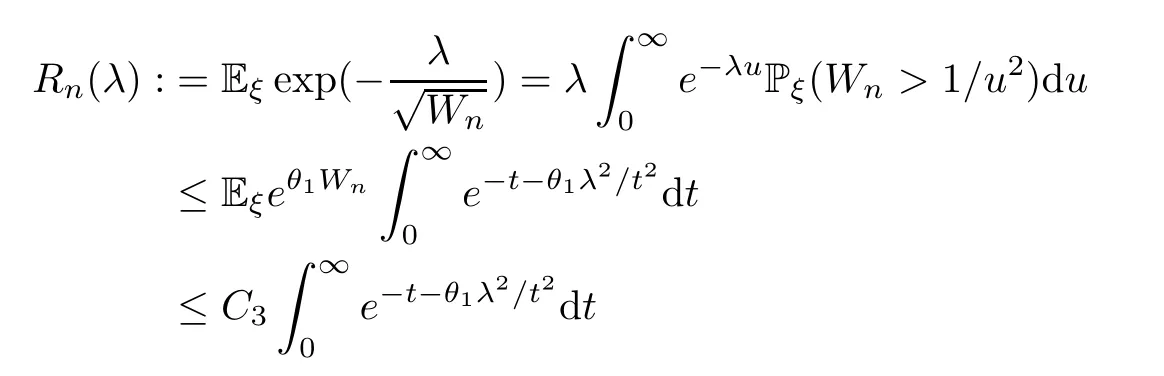
Finally，for 0＜θ2＜min{，1}，

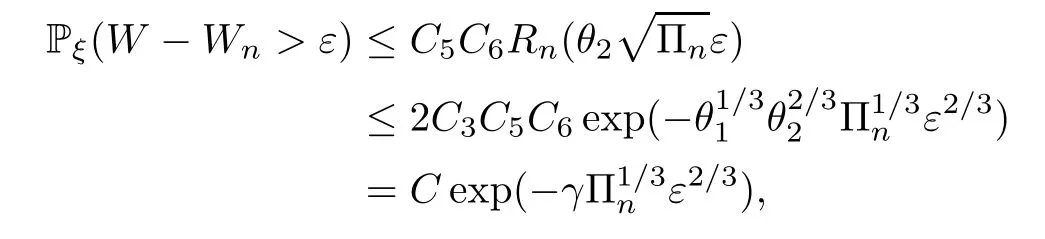
whereC=2C2C5C6＞0，.For Pξ(Wn-W＞ε)，the argument is similar.□

Proof of Theorem 2.2Notice that Eξeθ0W1depends only onξ0.Thus，whenξ0has a finite state space，the following three conditions are equivalent:

In addition，notice thatm0＞1 a.s.，since (2.8) holds，p0(ξ0)=0 andp1(ξ0)＜1 a.s..According to Lemma 4.2，there exist constantsθ1＞0 andC3＞0 such that supnEξeθ1Wn≤C3a.s..Therefore，part (a) is a direct consequence of Lemma 4.2.

For part (b)，by Lemmas 4.2，4.3 and 4.4，we can see that (2.11) holds.Taking the expectation in (2.11) and noticing the fact that Πn≥mn，we can get (2.12). □

5 Proof of Theorem 2.3

Then EξFn，i=0 and VarξFn.i=1.From Lemma 3.1，we see that

Lemma 5.1Forx∈R，let (rn)⊂N be a sequence of positive integers such thatrn→∞asn→∞.Suppose that (2.8) holds and that∞(ξ)∈(0，∞) a.s..Let

ProofLet

First，we prove that Esupx∈R|Pξ(Hn≤x)-Φ(x)|→0.By the stationarity of the environment sequence，we see that

Notice that (F1，i)i≥1are independent and identically distributed under Pξ，by the classic central limit theorem

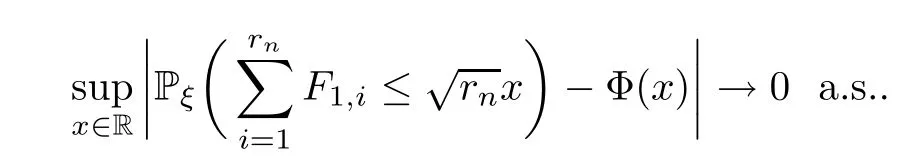
Thus，the dominated convergence theorem ensures that

Then，we prove thatIn→0 Pξa.s..By the independence betweenYn+j-1andunder Pξ，，we have

and taking the expectation，we have

and by calculating，

Sincern∈N withrn→∞，exist，for each subsequence{n′}of N withn′→∞，

and there exists a subsequence{n′′}of{n′}withn′′→∞such that

Finally，we prove that (3.8) holds.Since

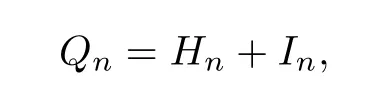
and we know thatIn′′→0 Pξa.s.，Qn′′converges toN(0，1) in law under Pξ，by Slutsky’s theorem (see Loeve[16])，Qn′′converges toN(0，1) in law under Pξ.Thus

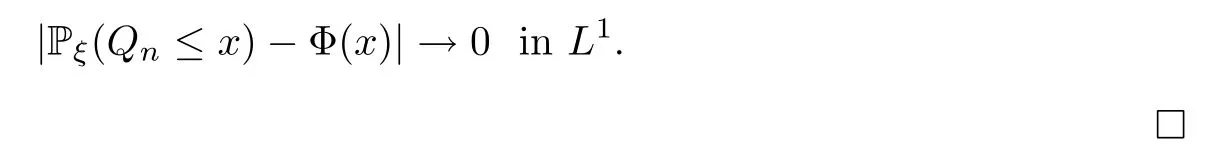
Proof of Theorem 2.3Set.Notice that (2.13) implies (2.14)，since

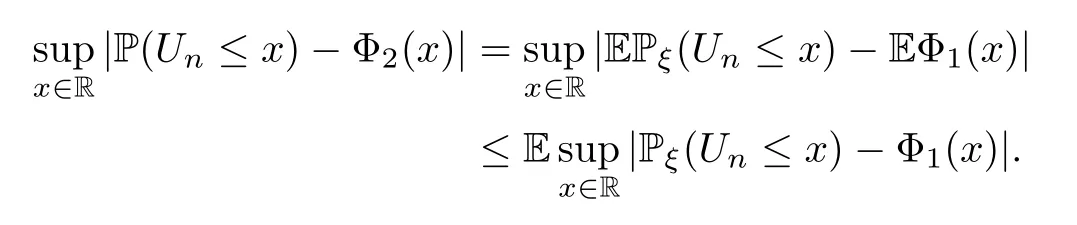
Thus we only need to prove (2.13).For simplicity，we suppose that Pξ(W＞0)=1 a.s.，in which case we have that.By (5.2)，

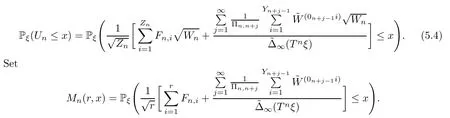
AsZnis independent ofFn，i(i≥1)，(0n+j-1i)(i，j≥1) under Pξ，it follows that

By Lemma 5.1，for each sequence (n′) of N withn′→∞，there exists a subsequence (n′′) of (n′) such thatn′′→∞and

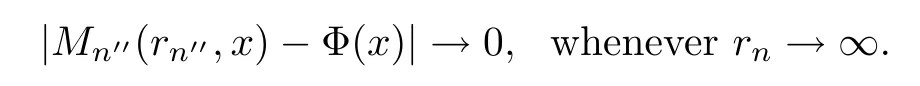
By (5.5) and the dominated convergence theorem，we can see that，for eachx∈R，

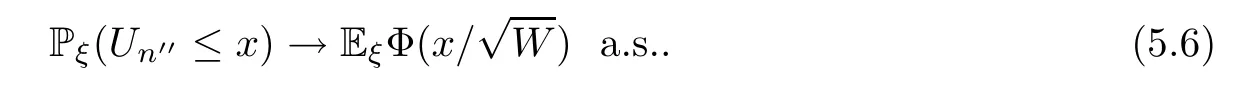
Therefore，(5.6) holds for all rationalxand for allx∈R，by the monotonicity of the left term and the continuity of the right term.Thus，by Dini’s theorem，

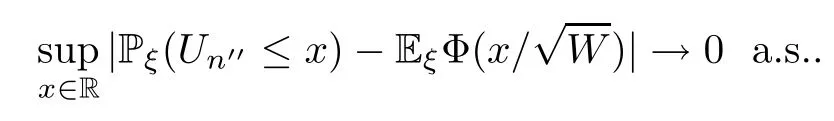
According to the dominated convergence theorem，

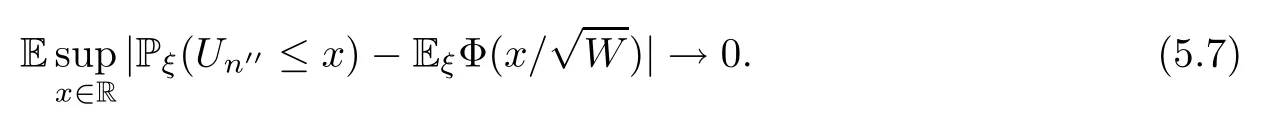
Therefore，we have proved that for each subsequence (n′) of N withn′→∞，there is a subsequence (n′′) of (n′) withn′′→∞such that (5.7) holds.Thus (2.13) holds. □

AcknowledgementsThe authors are grateful to the anonymous referees and Professor Quansheng Liu for very valuable comments and remarks which significantly contributed to improving the quality of the paper.