义务教育阶段几何直观分析框架

唐平 付天贵

摘 要 数学中的直观是借助于经验、观察、测试或类比联想所产生的对事物关系直接的感知与认识。几何直观是一种能力，主要是指利用图形描述和分析问题。从感知、理解、把握和推理四个水平建构了义务教育阶段几何直观的分析框架，框架为义务教育阶段学生几何直观的测试和发展研究奠定了基础。

关键词 义务教育 几何直观 分析框架

一、问题提出

发展学生的数学素养是数学课程改革的目标。为此，《义务教育数学课程标准（2011年版）》提出了要发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、模型思想、应用意识和创新意识。几何直观是标准提出的十个核心概念之一，它在内容、意义和方法上远远超过对几何图形本身的研究范畴，在平面几何、代数运算、解析几何、函数分析、概率统计、立体几何等领域都用到几何直观，它贯穿数学的整个领域和数学学习与研究的整个过程，成为近年来关注的热点。在CNKI数据库中以几何直观为主题进行文献检索，1951年至1959年有关文献有25篇，1960年至1966年有25篇，1967年至1979年有16篇（1967年至1975文献显示为0篇），1980年代至新世纪前10年每年文献见表1.

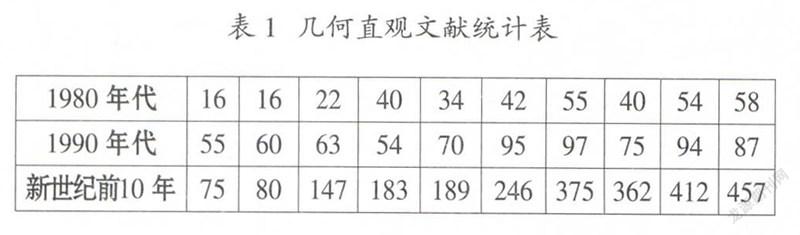
近5年，检索到的以几何直观为主题的相关文献分别是556篇、636篇、689篇、791篇、427篇（注：2015年文献只统计到8月份）。从文献统计可以看出，新课程实施以来，特别是《义务教育数学课程标准（2011年版）》颁布以来，几何直观受到数学教育界的广泛关注。

二、几何直观的内涵

早有研究论及直观和几何直观。1951年《人民教育》第三卷第一期刊登徐特立先生《各科教学法讲座》[1]一文，在论及辩证逻辑和形式逻辑的区别时，引用恩格斯用高等数学和初等数学的区别进行说明，“初等数学是技术的，因为它的数量是固定的、静止的，带直观性的，直接出来数量的，如算术、初等几何”，这是较早把直观概念与数学内容联系起来的文献。1952年中央教育部翻译室翻译的《苏联初等学校算术教学大纲》中提到学生获得直观几何的基本知识及实际应用这些知识的技能，认为学习几何教材，应该用直观教学法，并给学生一些实际经验[2]。其后，有研究者论述了直观教具的制作（胡元恺，1956；钱林坤，1958）。显然这里的直观几何是课程名称，直观教学法是一种教学方法。1982年，上海市数学会邀请法国科学院院士G.Choquet在上海市科学会给数学教师做报告，报告论及几何的作用和数学中的直观，在总结法国新数学的经验时，G.Choquet院士说：“在新数学的探索中，他们忘记了不经充分试验而作根本性改变总有极大风险的……这种想法使他们忘记了学生，忘记了直观，特别是几何直观的作用”[3]。这里出现了几何直观一词。此后，较多研究涉及几何直观。

直观是通过对客观事物的直接接触而获得的感性认识。对于几何直观，一种观点认为，几何直观是进行数学问题解决的方法。在此观点下，研究者研究了运用几何直观进行不同学段、不同领域的数学问题的理解和解决（李长明，1986；郑树钰，高洪义，杨贵林，1990；詹青松，1991；党四善，1999；华瑛，2011；王海侠，孙和军，2014；华旦玲，2014），或是研究借助几何直观加强数学教学的理解（王敬庚，1993；范秋君，1996；戴年宝，1999；黄伟星，顾晓华，2011；蔡宏圣，2013；宋晓燕，黄翔，2013；陈涛清，2015）。研究认识到了几何直观对于数学学习和理解的作用，但并未对几何直观是什么给予明确说明。一种观点认为几何直观是一种思维形式。徐本顺，商应钢（1984）认为，在科学创造的过程中，既有形象思维，又有抽象思维，另外还有介于二者间的中间环节，借助于几何直观进行思维就属于这样一个中间环节。几何直观既有形象思维，又有抽象思维，这是一种重要的思维形式。蒋文蔚（1997）认为，几何直观是一种思维形式，它是人脑对客观事物及其关系的一种直接识别或猜想的心理状态。也有研究者认为，几何直观是一种能力。数学中的直观是借助于经验、观察、测试或类比联想，所产生的对事物关系直接的感知与认识，几何直观是借助于见到的或想到的几何图形的形象关系产生对数量关系的直接感知[4]。2003年颁布的《普通高中数学课程标准（实验）》明确提出要培养和发展学生的几何直观能力；《义务教育数学课程标准（2011年版）》也指出：几何直观主要是指利用图形描述和分析问题。几何直观是一种能力的观点得到国内学者广泛的认同[5]。

由此可见，几何直观就是利用图形描述和分析问题，它是一种能力，几何直观能力就是利用图形描述问题、分析问题、解决问题的能力。几何直观是在直观感知的感性基础之上所形成的理性思考。由于数学的研究对象是空间形式和数量关系，所以几何直观就是学习者借助于图形的形象关系对空间形式和数量关系进行感知、理解和把握，是学习者对于数学对象的几何属性或与几何属性密切相关的一些属性的整体把握和直接判断。几何直观研究对象超越几何图形本身研究范畴，包括了数与代数、图形与几何、统计与概率学科领域。

三、几何思维水平研究

20世纪50年代，荷兰学者范·西尔夫妇研究了几何思维的发展，建构了几何思维发展的模式，该模式由认识、分析、非正式演绎、正式演绎、严密5个水平构成。范·西尔夫妇对每一水平都进行了描述，并指出这些水平是非连续的。然而，研究者研究了范·西尔的几何思维水平，指出这些水平是动态的、连续的[6]。Gutierrez和Jaime（1987）通过对职前教师的测量，证明了水平1到水平4的存在和层次性，但他们认为水平5（严密性）有待进一步的研究确认[7]。结合后来的研究成果，80年代，范·西尔将几何思维水平整合为直观水平、描述水平和理论水平。直观水平是指整体地认识几何对象；描述水平是指通过几何性质去描述几何对象；理论水平是指通过演绎去证明几何关系。阿伦·霍夫（1981）研究了几何中的技能，认为视觉方面的技能、语言方面的技能、绘图方面的技能、逻辑方面的技能、应用方面的技能这5个方面的技能是重要和需要训练的，他把这5方面的技能与范·西尔几何思维5水平整合，形成了5×5几何技能模式。虽然范·西尔和阿伦·霍夫未直接研究几何直观，同时他们的研究只局限于几何学科领域，但他们的研究为几何直观研究奠定了基础。

国内对几何思维水平的研究，几乎都以范·西尔几何思维模式为基础。张和平、李俊央和项昭（2007）研究了义务教育初中数学课程中的几何直观性水平，同时调查了初中生几何直观性水平，根据他们的研究，初中学生几何直观水平很难达到严密水平。冯雪娇、金美月（2011）从直观水平、描述水平和理论水平三个方面研究了多元文化背景下初中生几何认知水平，发现学生都能达到直观水平，而不能达到描述和理论水平。卢英和黄燕萍（2014）从几何图形的观察、分解、组合和想象四个方研究了初中生几何思维水平的发展。

四、几何直观分析框架

几何直观是一种能力，是学习者借助于图形的形象关系对空间形式和数量关系进行感知、理解、把握和推理的能力。数学学习、研究过程中，人们常借助几何直观去描述问题、分析问题、解决问题。以范·西尔几何思维水平和阿伦·霍夫几何直观技能为基础，结合几何直观的内涵，可以建构起如表2的直观分析框架。

在中小学数学教育教学活动中，几何直观不仅体现在教学理念的层面，更体现在数学学习活动中，学生通过如拼图、折纸、画图等活动，加深对所学数学知识的认识和理解，进行判断和推理。义务教育数学课程标准把结果性目标分为了解、理解、掌握和运用四个水平，并对每个水平进行了描述。以上所建构的几何直观分析框架，与义务教育课程标准课程目标相对应，为义务教育阶段学生几何直观能力测试和研究学生几何直观发展奠定了基础。

参考文献

[1] 徐特立.各科教学法讲座[J].人民教育，1951（1）.

[2] 中央教育部翻译室.苏联初等学习算学大纲[J].人民教育，1952.

[3] G.Choquet.几何和直观在数学中的作用[J].史数中，译.数学通报，1982（2）.

[4] 徐利治.谈谈我的一些数学治学经验[J].数学通报，2000（5）.

[5] 史宁中，孔凡哲.关于几何直观的含义与表现形式[J].课程·教材·教法，2012（7）.

[6] Burton，L.，Cooper，M.，& Leder，G..Representations of three-

dimensional figures by mathematics teachers-in-trainging.In Univ. of London Institute of Education （Eds.），Proceedings of the 10th PME International Conference，1986（1）.

[7] Gutierrez，A.，& Jaime，A.Estudio de las caracteristicas de los nivele de Van Hiele.In J.G.Bergeron，N.Herscovics，& C.Kieran（Eds.），Proceedings of the 11th PME International Conference，1987（3）.

[作者：唐平（1979-），女，重庆永川人，重庆文理学院数学与财经学院讲师，硕士；付天贵（1969-），男，重庆酉阳人，重庆文理学院数学与财经学院副教授，西南大学数学与统计学院在读博士研究生。]

【责任编辑 陈国庆】