摆动电弧焊的数学模型研究与仿真

李　炼，王守华

(桂林电子科技大学 信息与通信学院，广西 桂林　541004)



摆动电弧焊的数学模型研究与仿真

李炼，王守华

(桂林电子科技大学 信息与通信学院，广西 桂林541004)

针对熔敷铁水流动引起的焊缝坡口内熔池变化带来的焊缝跟踪精度降低的问题，提出一种斜线和二次抛物线相结合的V+U型焊缝坡口模型。该模型采用分段曲线融合方法改进焊缝坡口形状，并在SIMULINK建立的数学模型进行焊缝坡口跟踪的仿真实验。实验结果表明，改进的焊缝坡口模型的焊接电流与实际焊接电流的差值波动更小，更接近实际焊缝坡口形状。

熔敷铁水；焊缝跟踪；V+U型；曲线融合

近年来，随着焊接自动化水平的不断提高，现代工业控制领域对焊接的精度和稳定性提出了更高要求。焊接智能化和自动化成为不可改变的发展趋势，焊缝自动跟踪技术是实现焊接智能化和自动化必须认真对待的研究课题[1-2]。焊缝坡口位置的实时监测和焊接电弧的位置调整是焊缝自动跟踪需要解决的问题，而焊缝坡口和电弧的相对位置又必须通过传感器获取，不同的传感方式决定了获取的相对位置精确度高低。目前国内外应用于焊缝自动跟踪技术的电弧传感方式有摆动电弧传感方式[3]、旋转电弧传感方式[4]、磁控电弧传感方式[5]。摆动电弧焊的研究主要集中在对位置偏差的检测和处理上[6-8]。建立摆动电弧焊焊缝坡口数学模型是计算位置偏差的有效方法，V型不对称坡口[9-10]和熔池扰动引起的工件形状不规整都会对焊缝跟踪造成不利影响，甚至出现跟丢和误判情况。

鉴于此，分析熔池扰动引起的工件形状变化，应用SIMULINK建模和仿真，得到焊炬高度变化规律，推算出的焊接仿真电流与实际焊接电流作比较，验证模型的正确性。

1　摆动电弧焊

焊接电弧在焊缝中心线周围来回扫描引起焊炬高度有规律性地变化，检测扫描过程中的参数，判断偏离方向和计算偏离量，电弧传感器工作示意如图1所示。当摆动的电弧沿着工件坡口的一端向焊缝中心线运动，焊炬高度随之变大；当电弧偏离焊缝中心线向工件坡口另一端运动时，焊炬高度也随之变小。焊矩高度发生变化，势必会引起焊接电流的相应变化。如图2所示，焊炬高度H1>H>H2，而焊接电流I1>I>I2[8]。

图1　电弧传感器工作示意图Fig.1　Schematic diagram of arc sensor

图2　电流随焊炬高度变化Fig.2　Current variation with the torch height

工件之间的对接处进行电弧焊接时，坡口的形状往往以V字型呈现，称之为V型坡口。如图3所示，以坡口的中心B为摆动起始点，摆动左右边缘A、C为停靠位置，焊枪头在1个周期内的摆动可分为BC、CB、BA、AB共4个阶段。若V型坡口完全对称，在同一水平线的焊炬高度将保持一致，理论上两侧平均电流值也一致。但实际生产的工件通常与上述模型不完全相符，V型坡口两侧的角度会随工件的不同而有所变化，熔敷铁水流动会使V型坡口改变原有形状。摆动电弧焊在工件和熔池之上往返运动，引起焊炬高度和焊接电流的变化。

图3　坡口模型Fig.3　Groove model

2　建模与仿真

用于焊接的母材边沿通常呈斜坡状，母材靠拢后形成V型坡口。摆动电弧焊对V型坡口来回扫描，一些尚未完全融化的焊接母材与用于填充的金属在焊缝底部形成了具备一定几何特征的液态金属区，这个区域叫熔池[11]。传统的焊缝跟踪模型忽略了熔池对跟踪精度的影响。工件边沿本身的形状，也就是通常所说的V型坡口，不能完全反映实际焊接情况。焊炬高度H应该由工件高度加上熔池高度，熔池内液态金属的流动可以近似模拟成一条平滑的二次抛物线，这就是U型坡口模型。U型坡口相比V型坡口一定程度上更真实地反映焊缝跟踪过程。但是熔池内液态金属区只集中在熔池底部中间的一小块区域，而工件边沿的上半部分并未被液态金属覆盖。将V型坡口模型和U型坡口模型相结合，焊缝坡口的下半部分(被熔池覆盖的区域)用近似的平滑二次曲线替代，坡口的上半部分(未被熔池覆盖的区域)仍然保持工件坡状。边沿呈斜坡状的母材存在坡度不一样情况，也就是焊缝扫描两边不对称。坡度不同导致焊缝中心线两侧的熔池区域宽度也不同，熔池区域在中心线两侧的区域各需一条二次曲线替代。

2.1V+U型坡口焊炬高度的变化规律

焊炬高度是指摆动电弧焊接扫描过程中焊枪头到工件表面的垂直高度。V+U型坡口模型是在V坡口模型上加以改进，研究在不同的摆动频率下，焊缝偏差e、焊缝左右两侧坡口斜度α和β、焊枪摆动幅度r以及熔池位于焊缝中心线两侧宽度a、b等参数对焊炬高度H的变化规律。

如图4所示，C为焊枪头摆动的中心位置，此时焊缝偏差为左偏e个单位。A和E为焊枪扫描区间的左右两侧极限位置，B和D为熔池区域的左右边界，BC为焊缝中心线左侧熔池，CD为右侧熔池。假定焊枪先从摆动中心位置B向右扫描，摆动到右极限位置E返回，到左极限A后再折回至B。位置B向右扫描开始计时，可分为7个时间点：

图4　U+V坡口摆动电弧扫描示意图Fig.4　Schematic diagram of U+V groove swing arc scanning

以焊缝中心线为竖轴，垂直方向为横轴，两侧工件斜坡的交点为原点建立直角坐标系。焊枪头移动速度为Vx，一个扫描周期T=4r/Vx，计算焊炬高度随时间t的变化规律为：

(1)

根据文献[12],焊接过程的实际焊接电流值应分为2个部分，一部分为不变化的初始工作点的电流，另一部分为随焊炬高度变化的电流。实际焊接电流等于2个部分之和：

(2)

根据式(1)、(2)，得出一个周期内焊接电流变化规律为：

2.2V+U型坡口SIMULINK建模仿真

坡口模型的扫描区间被5个点分为4段子区间，而扫描的整个过程需要往返一次，所以一个周期内有8个子区间。对式(1)、(3)建立仿真模型，框图如图5所示。

图5　V+U型坡口焊缝模型框图Fig.5　Block diagram of V+U type groove weld model

该模型由Select子模块完成扫描区间的选择，每个时间点只允许seg1～seg8中一个信号有效，选中BC、CD、DE、ED、DC、CB、BA、AB对应的8个模块计算出焊炬高度值。通过关系处理符将运行时间t和分割区间的时间点t1～t7在一个周期长度T=4r/Vx分为8个子区间。Select子模块输出连接的8个模块分别表示式(1)中8个分段函数，BC_Model子模块展开如图6所示。

图6　BC_Model子模块Fig.6　Sub module of BC_Model

Matlab Fcn中函数

(4)

的执行功能为：

(5)

其中对应位置赋值：u(1)=a，u(2)=Vx，u(3)=t，u(4)=α，u(5)=Hp，u(6)=h。参考式(3)，将H(t)转化为I(t)输出。

3　实验结果分析

对V型坡口、U型坡口、V+U型坡口采用SIMULINK分别进行仿真，焊炬高度H(t)和焊接电流I(t)随时间t在一个周期内的变化规律如图7所示。其中：各参数值为e=3，r=6，Vx=24(T=1)，α=30，β=45，Hp=10，h=0.5，a=2，b=1。不难看出，由于忽略焊接过程中熔池的影响，图7(a)中V型坡口模型焊接电流变化过于尖锐；图7(b)中U型坡

图7　I(t)随t变化规律Fig.7　I(t) variation with t

口模型则将整个焊缝理想化为二次抛物线，扩大了熔池覆盖的区间范围，导致电流过于理想化；而图7(c)中V+U型坡口模型熔池覆盖的区间范围适中，靠近熔池中心位置的电流变化较平滑，远离熔池中心位置的变化较尖锐，符合焊缝坡口的实际情况。

为进一步验证仿真结果的可靠性，焊接实验将焊接的实际参数与仿真参数设置成一致，文献[13]中实际焊接电流波形如图8所示，实际焊接的焊缝边沿电流呈线性变化，焊缝中心位置的电流变化则更为平滑。

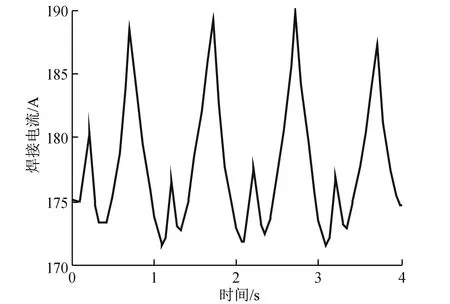
图8　实际焊接电流波形Fig.8　Actual welding current waveform

将实际焊接电流与3种坡口模型的仿真电流取0～4 s内4个周期作差，得出电流差值变化幅度随时间变化规律，差值分别设为Eu、Ev、Ev+u，如图9所示。V+U坡口建模方法仿真电流波形与实际焊接电流波形变化规律基本一致。分别求出E的均方差Estd, u=3.643 7，Estd, v=1.821 8，Estd, u+v= 1.214 6。从3种坡口模型仿真的焊接电流差值的幅度变化情况，反映出V+U型坡口模型更接近实际焊缝坡口形状。

图9　电流差值变化Fig.9　Variation of current difference

4　结束语

根据实际的工件和熔池形状建立V+U坡口数学模型。实验仿真表明，相比原有的V型坡口模型和U型坡口模型，仿真焊接电流更接近实际焊接电流，V+U坡口模型更能真实反映焊缝坡口形状。

[1]廖家平，张晨曙，尹懿.焊接机器人焊缝跟踪技术的发展状况及趋势[J].现代焊接，2010(4):1-3.

[2]ZHOU H,MA B.Path following control of tractor-trailers with off-axle hitting[J].Chinese Control Conference,2007:283-286.

[3]吴金锋.基于摆动电弧传感器的焊缝跟踪技术研究[D].北京：北京理工大学，2012:16-20.

[4]高延峰，张华，毛志伟.以旋转电弧为传感器的移动机器人角焊缝跟踪[J].机械工程学报，2009,45(9):64-71.

[5]魏复理，洪波，洪宇翔.磁控电弧传感器焊缝跟踪技术研究[J].机械科学与技术，2008,45(12):1586-1590.

[6]吴晓明，唐衡郴，王陆钊，等.铝合金自动焊接焊缝跟踪技术研究[J].电焊机，2013,43(10):59-62.

[7]周玉印，付丽君，池世春，等.基于模糊控制的电弧焊接焊缝跟踪技术研究[J].工业控制计算机，2013,126(11):71-72.

[8]KAM B O,JEON Y B,SUH J H.Motion control of two-wheeled welding mobile robot with seam tracking sensor[J].International Journal of the Korean Society of Precision Engineering,2003,4(2):30-38.

[9]FRAGA R,LIU S.Double fuzzy logic control for the ship path following[C]// The 2nd International Conference on Intelligent Control and Information Processing,2011:92-96.

[10]洪波，黄俊，潘际銮，等.摆动电弧埋弧焊的数学建模与仿真[J].焊接学报，2007,28(6):25-29.

[11]潘际銮.现代弧焊控制[M].北京:机械工业出版社，2000:103-104.

[12]雷跃.基于电弧传感焊缝跟踪的偏差信息监测[J].电子测试，2012(4):1-5.

[13]祝团结.摆动电弧CO2焊焊缝跟踪精度研究[D].湘潭：湘潭大学，2012:15-17.

编辑：梁王欢

Research and simulation of the swing arc mathematical model

LI Lian, WANG Shouhua

(School of Information and Communication Engineering, Guilin University of Electronic Technology, Guilin 541004, China)

A V+U type weld model based on diagonal and parabolic is presented to improve seam tracking with molten iron flow in weld pool. A subsection curve fusion strategy is utilized for establishing pool model and tracking test by SIMULINK mathematical model. The experimental results show that compared with other models, the current deviation is smaller and the groove shape is more real.

molten iron; seam tracking; V+U type; fusion curve

2016-01-12

桂林电子科技大学研究生教育创新计划(GDYCSZ201460)

王守华(1976-)，男，山东滨州人，副教授，研究方向为信号处理、卫星导航。E-mail：hwafly@guet.edu.cn

TN967.1

A

1673-808X(2016)03-0194-05

引文格式： 李炼，王守华.摆动电弧焊的数学模型研究与仿真[J].桂林电子科技大学学报，2016,36(3)：194-198.