F-Gorenstein投射复形类的稳定性

刘仲奎,叶星美

(西北师范大学数学与统计学院,甘肃兰州　730070)



F-Gorenstein投射复形类的稳定性

刘仲奎,叶星美

(西北师范大学数学与统计学院,甘肃兰州730070)

F-投射复形;F-Gorenstein投射复形

(1)子范畴C关于F-扩张封闭;

(2)如果短正合列0→A→B→C→0是F-正合的,且B,C∈C,那么A∈C;

(3)C包含P(F).

2　投射复形

证明与文献[10]命题4.1类似.】

命题2设X是F-Gorenstein投射模的复形.则存在复形的F-正合列0→X→U→K→0,其中U是F-投射复形,K是F-Gorenstein投射模的复形,使得对任意F-投射复形V,F-正合列0→X→U→K→0是Hom(Λ)(-,V)正合的.

证明设

是F-Gorenstein投射模的复形,即对任意的n,Xn是F-Gorenstein投射模,由F-Gorenstein投射模的定义知,存在F-正合复形：

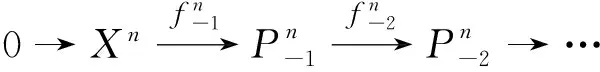
因为ε和θ是正合的,且存在态射1和(1,0),所以存在态射h使上图交换.显然ε是h,η的拉回.又因为F对拉回封闭,θ是F-正合的,所以ε是F-正合的.考虑以下交换图

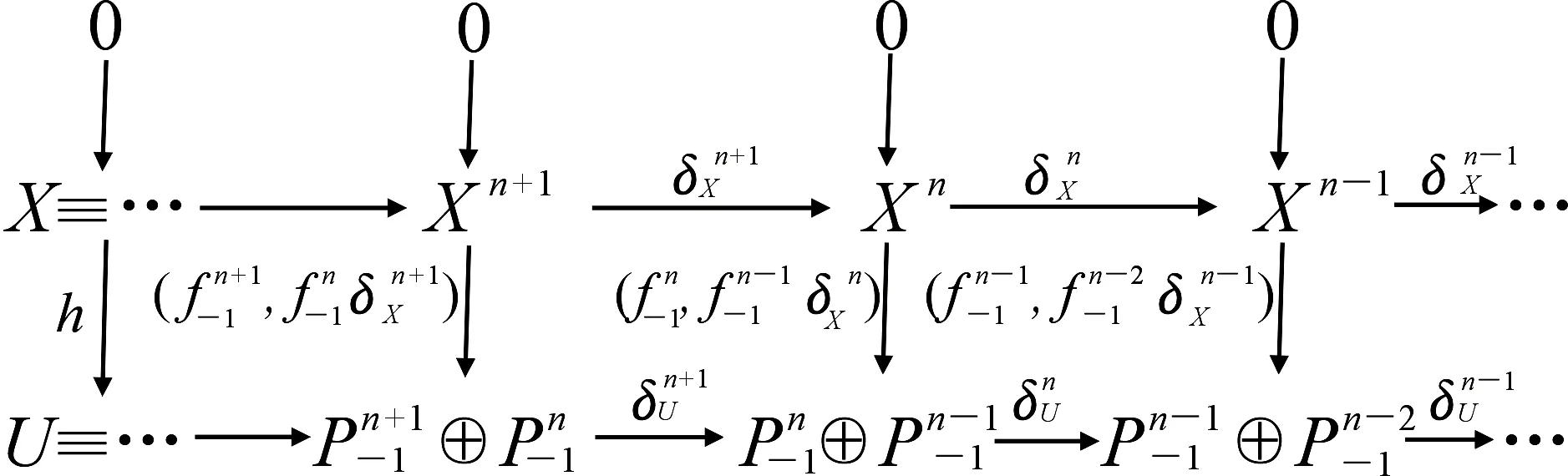
因为K-n-1是F-Gorenstein投射模,所以下行满,于是上行也满.因而0→Hom(Λ)(K,V)→Hom(Λ)(U,V)→Hom(Λ)(X,V)→0正合.故0→X→U→K→0为所证的复形的F-正合列.】

命题3设X是F-Gorenstein投射模的复形.则存在复形的F-正合列0→T→U→X→0,其中U是F-投射复形,T是F-Gorenstein投射模的复形,使得对任意F-投射复形V,F-正合列0→T→U→X→0是Hom(Λ)(-,V)正合的.

证明设

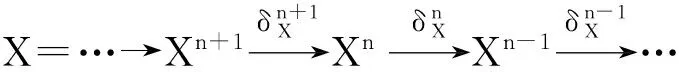
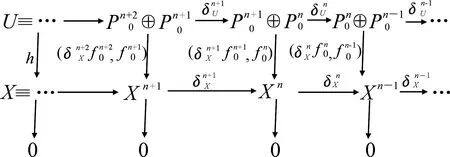
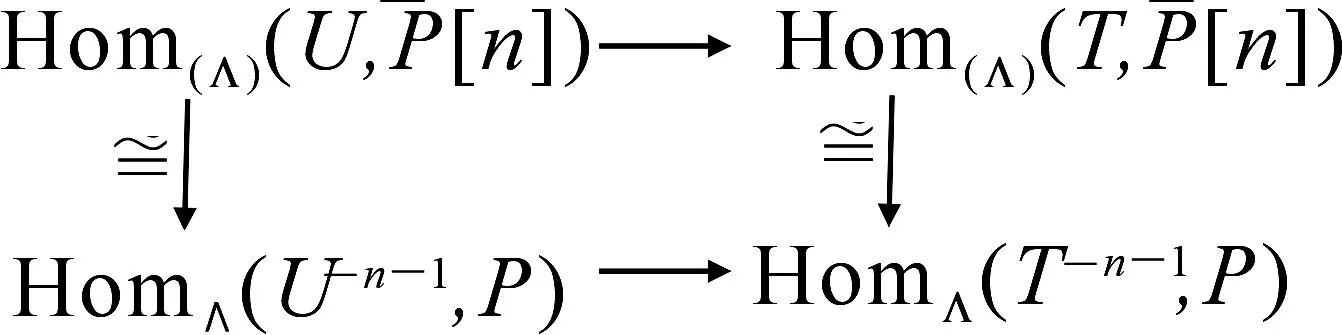
因为T-n-1是F-Gorenstein投射模,所以下行满,于是上行是满.因而0→Hom(Λ)(X,V)→Hom(Λ)(U,V)→Hom(Λ)(T,V)→0正合,故0→T→U→X→0为所证的复形的F-正合列.】

定理1复形X是F-Gorenstein投射复形当且仅当对任意的m,Xm是F-Gorenstein投射模.

引理1F-Gorenstein投射复形是F-可解子范畴,且关于直和与直和因子封闭.

证明由定理1知,复形X是F-Gorenstein投射复形，当且仅当每个层次Xm是F-Gorenstein投射模,又由文献[4]知,GP(F)是F-可解子范畴,且关于直和与直和因子封闭.则F-Gorenstein投射复形是F-可解子范畴,且关于直和与直和因子封闭.】

3　F-Gorenstein投射复形类的稳定性

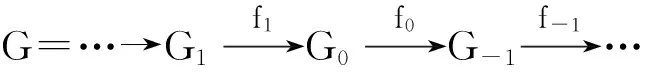
(1)每个Gi是F-Gorenstein投射复形;

(2)X≅kerf-1;

(3)对任意的F-投射复形P,复形G是Hom(Λ)(-,P)正合的.

注1易见F-Gorenstein投射复形类包含于F-Gorenstein G-投射复形类.

命题4设X是复形,n是正整数,

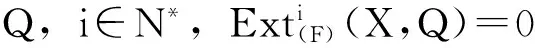
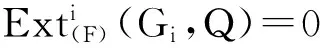
(2)设X是F-Gorenstein G-投射复形,Q是F-投射复形.则存在Hom(Λ)(-,Q)正合的F-短正合列0→N→G→X→0,其中G是F-Gorenstein投射复形,N是F-Gorenstein G-投射复形.另外有长正合列

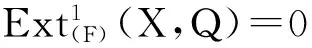
定义4称复形X是强F-Gorenstein G-投射复形,如果

(1)存在F-短正合序列0→X→G→X→0,其中G是F-Gorenstein投射复形;

(2)对任意的F-投射复形Q,函子Hom(Λ)(-,Q)保持上述序列的正合性.

命题5F-Gorenstein G-投射复形是强F-Gorenstein G-投射复形的直和因子.

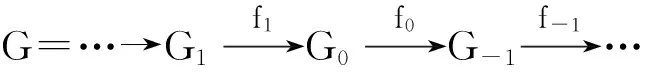
定义5设X是强F-Gorenstein G-投射复形.如果存在F-短正合列0→X→N→H→0,其中H是F-Gorenstein投射复形,那么称复形N是X-型复形.

命题6设复形X是强F-Gorenstein G-投射复形,N是X-型复形.则

(2)存在F-短正合列0→N→L→K→0,其中K是X-型复形,L是F-投射复形.

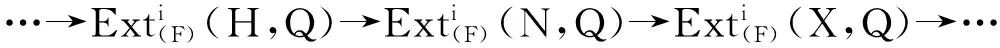
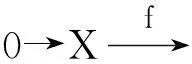
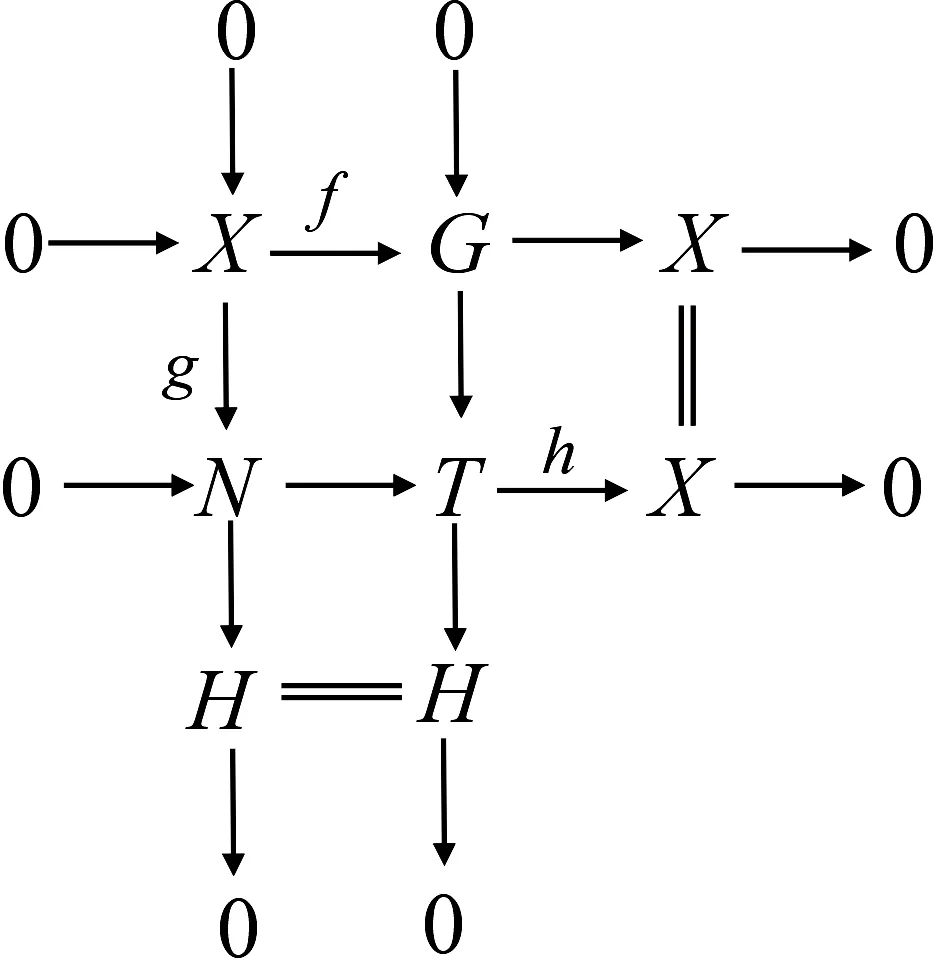
图1　同态f与同态g的推出图

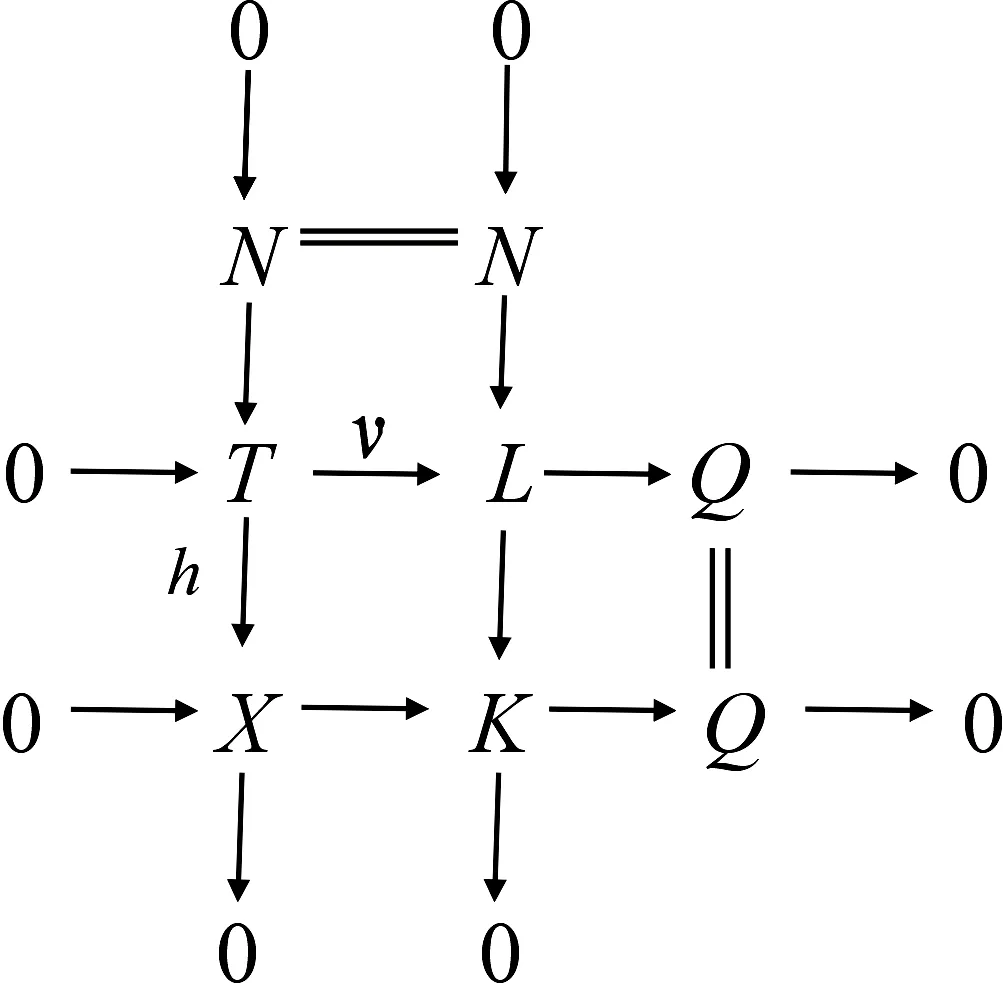
图2　同态h与同态v的推出图

命题7X-型复形是F-Gorenstein投射复形.

证明设N是X-型复形,由命题6(2)知,存在F-短正合列0→N→L0→K→0,其中L0是F-投射复形,K是X-型复形,且对任意的F-投射复形Q,上述F-短正合列是Hom(Λ)(-,Q)正合的.对K重复上述过程,可得F-正合序列G:0→N→L0→L-1→L-2→…,并且G是Hom(Λ)(-,Q)正合的.结合命题6(1)可知N是F-Gorenstein投射复形.】

定理2F-Gorenstein G-投射复形是F-Gorenstein投射复形.

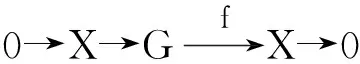
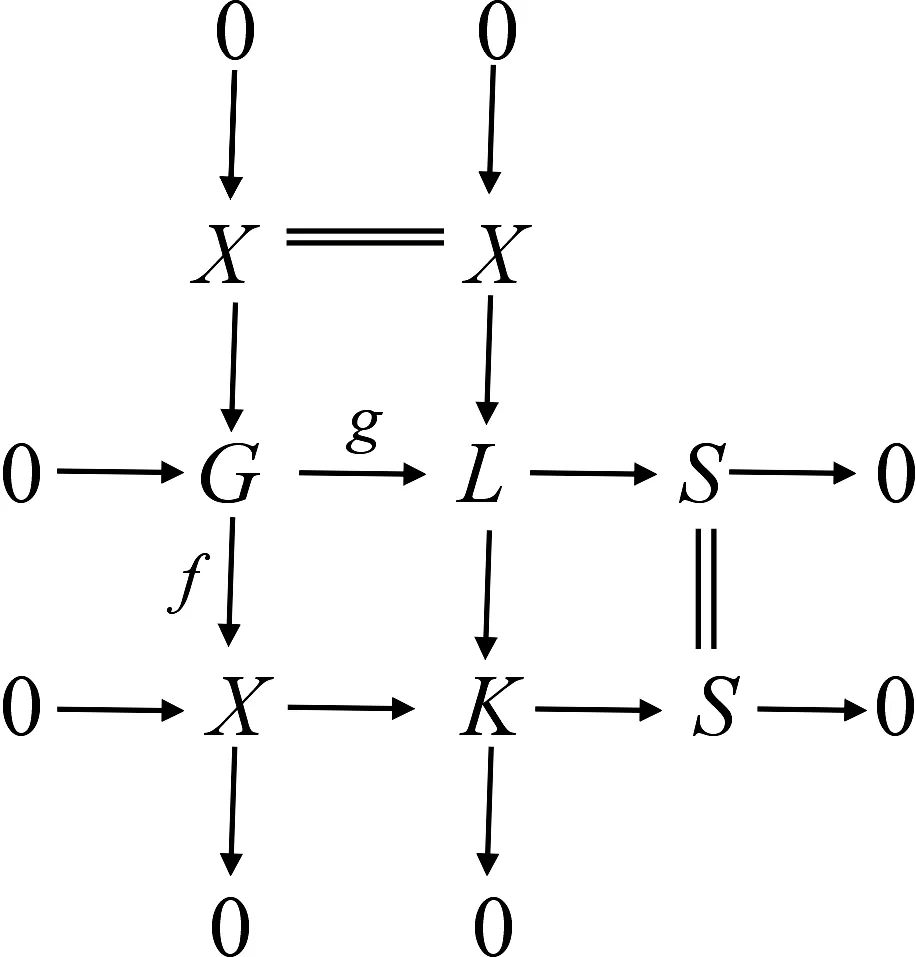
图3　同态f与同态g的推出图

[1]AUSLANDER M,SOLBERG Ø.Relative homology and representation theory I.Relative homology and homologically finite subcategories[J].Comm Algebra,1993,21(9):2995.

[2]AUSLANDER M,SOLBERG Ø.Relative homology and representation theory Ⅱ.Relative cotilting theory[J].Comm Algebra,1993,21(9):3033-3079.

[3]AUSLANDER M,SOLBERG Ø.Relative homology and representation theory Ⅲ.Cotilting modules and weddrburn correspondence[J].Comm Algebra,1993,21(9):3081-3097.

[4]TANG X.On F-Gorenstein dimensions[J].J Algebra Appl,2014,13(6):1450022(1-14).

[5]SATHER B,SHARIF T,WHITE D.Stablily of Gorenstein categories[J].J London Math Soc,2008,77(2):481.

[6]SAMIR B.Stablily of Gorenstein classes of modules [J].Algebra Colloquium,2013,20(4):623.

[7]ENOCHS E E,JENDA O M G.Relative Homological Algebra[M].Berlin:de Gruyter,2000.

[8]ROTMAN J J.An Introduction to Homological Algebra[M].New York:Academic Press,1979.

[9]ANDERSON F W,FULLER K R.Rings and Categories of Modules[M].New York:Springer,1992.

[0]YANG C,LIANG L.Gorenstein injetive and projective complexes with respect to semidualizing module[J].Comm Algebra,2012,40(9):3352.

(责任编辑陆泉芳)

Stability of F-Gorenstein projective complexes

LIU Zhong-kui,YE Xing-mei

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)

F-projective complexes;F-Grenstein projective complexes

10.16783/j.cnki.nwnuz.2016.02.001

2015-07-10;修改稿收到日期:2015-11-20

国家自然科学基金资助项目(11361050)

刘仲奎(1963—)，男，甘肃通渭人，教授，博士，博士研究生导师.主要研究方向为同调代数和环理论.

E-mail:liuzk@nwnu.edu.cn

O 153.3

A

1001-988Ⅹ(2016)02-0001-05