T型非抢占优先权MM1排队系统
2016-09-07马占友张世久
马占友,张世久,徐 彪
(燕山大学理学院,河北秦皇岛 066004)
T型非抢占优先权MM1排队系统
马占友,张世久,徐彪
(燕山大学理学院,河北秦皇岛066004)
为了进一步优化认知无线网频谱的接入,在将T作为时间参数引入排队系统的基础上,提出了一种新的T型非抢占优先权排队策略,并将其引入M/M/1排队模型中,系统分析并推导出顾客在系统内的平均等待时间、平均逗留时间以及系统的平均队长.最后通过Matlab软件对顾客平均等待时间进行了仿真模拟.
M/M/1排队系统;优先权;T型非抢占优先权;认知无线网
0 引言
随着无线通信应用的不断发展,固定的频谱接入方式已经越来越凸显它的不足,很多学者和工程技术人员都在研究认知无线网络的优化问题.使得主用户与次用户的频谱接入更加合理是提高无线通信效率的重中之重[1],而这就需要运用优先权排队论做进一步研究.
2006年,唐应辉等[2]简单介绍了抢占和非抢占优先权排队系统,文献[3,4]研究了具有抢占优先权的M/M/1排队系统,并得出相应的性能指标.2012年,Kim[5]提出了新的T型抢占优先权排队策略并分析了系统的性能,文献[6]进一步讨论了非抢占有限优先权M/M/1排队系统及其性能指标.
本文在现有研究的基础上讨论T型非抢占优先权M/M/1排队系统及其在认知无线网络频谱选择中的应用.频谱接入技术中的网络信息用户分为主用户和次用户两个等级,在抢占优先权排队当中,如果主用户较多,则次用户的平均等待接入时间就会大大增加,导致次用户长时间等待,频谱资源利用率降低,达不到共享目的,因此需要对抢占优先权排队方式进行优化,进而使得次用户在合理情况下接入频谱.
1 模型描述
T型非抢占优先权M/M/1排队模型描述如下:
(i)假设系统中的主用户和次用户分别表示为ClassⅠ和ClassⅡ,其中ClassⅠ优先权高于ClassⅡ.两个等级的顾客各自独立地按照Poisson过程到达系统,其参数分别为λ1和λ2;系统中顾客的服务时间服从参数为μ的指数分布,所以每位顾客的平均服务时间为1/μ.
(ii)设ρi=λi/μ表示服务强度,i=1,2;ρ=ρ1+ρ2,λ=λ1+λ2;Si为第i级顾客所需的服务时间,E(Si)=1/μ,i=1,2;T为时间参数,且T≥1/μ.在为ClassⅠ顾客服务时,系统每隔时间T就会将队伍中首位ClassⅡ顾客插入队伍中并为其服务,而正在被服务的ClassⅠ顾客则被中止,等待插入的ClassⅡ顾客服务完毕再继续;而系统在被中止的ClassⅠ顾客重新接受服务时重新开始计时,时间T之后再插入ClassⅡ顾客并为其服务;此后重复前面的过程,直至系统中没有顾客(如图1).当时间T内所有ClassⅠ顾客都被服务完后,ClassⅡ顾客自动按照先到先服务的顺序接受服务.
(iii)假设同类顾客按照先到先服务(FCFS)规则接受服务,ClassⅠ比ClassⅡ有优先权,顾客的到达与服务过程独立.

图1 系统开始服务后ClassⅠ顾客和ClassⅡ顾客的排队情况
2 系统性能分析
令Lqi是第i级顾客的平均等待人数,Wqi是第i级顾客的平均等待服务时间,i=1,2.
2.1顾客在系统中的平均等待时间
因顾客分为两个等级,所以本文也分为两种情况进行讨论.
2.1.1到达系统的顾客为ClassⅠ顾客A当到达系统的顾客为ClassⅠ时(如图2),将ClassⅠ顾客分为三种不同的情形:(X1),(X2)和(X3).
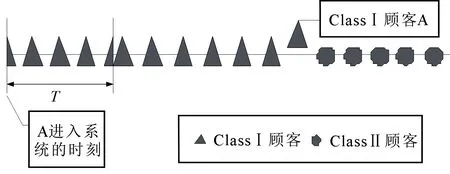
图2 ClassⅠ顾客A进入系统时顾客的排队情况
设Lq1xj表示(Xj)情形下ClassⅠ顾客的平均等待队长,Wq1xj表示(Xj)情形下ClassⅠ顾客的平均等待时间,其中j=1,2,3.
(X1)顾客A进入系统时ClassⅡ顾客足够满足按照时间间隔T插队.在这种情况下,顾客A的平均等待时间Wq1x1为以下三个时间之和:
因此,
(1)
(X2)顾客A进入系统时,ClassⅡ顾客不足够满足按照时间间隔T向前插队,加上顾客A等待被服务的过程中新进入系统的ClassⅡ顾客还是不足够按照时间间隔T向前插队,则顾客A的平均等待时间Wq1x2为以下三个时间之和:
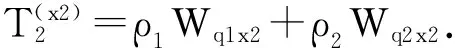
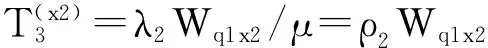
因此,
(2)
(X3)顾客A进入系统时,ClassⅡ顾客不足够满足按照时间间隔T向前插队,但是在顾客A等待服务的过程中新进入系统的ClassⅡ顾客足够满足按照时间间隔T向前插队,则顾客A的平均等待时间为以下三个时间之和:
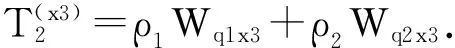
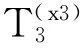
因此,
(3)
2.1.2到达系统的顾客为ClassⅡ顾客B当到达系统的顾客为ClassⅡ时(如图3),ClassⅡ顾客分为三种不同的情形:(Y1),(Y2)和(Y3).

图3 ClassⅡ顾客B进入系统时顾客的排队情况
设Lq2yj表示(Yj)情形下ClassⅡ顾客的平均等待队长,Wq2yj表示(Yj)情形下ClassⅡ顾客的平均等待时间,其中j=1,2,3.
(Y1)顾客B进入系统时,系统中的ClassⅡ顾客不足够满足按照时间间隔T插队,此时顾客B的平均等待时间Wq2y1为以下三个时间之和:
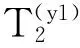
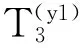
因此,
(4)
(Y2)顾客B进入系统时,系统中的ClassⅡ顾客足够满足按照时间间隔T插队,此时顾客B的平均等待时间Wq2y2为以下三个时间之和:
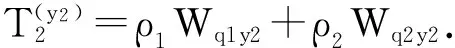
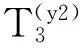
因此,
(5)
(Y3)顾客B进入系统时,系统中的ClassⅡ顾客足够满足按照时间间隔T插队,但在顾客B等待被服务的时间里,新到达的ClassⅠ顾客使得ClassⅡ顾客不再足够按照时间间隔T插队,这时Wq2y3为以下三个时间之和:

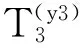
因此,
(6)
从式(1),(3)式和(4),(6)式中解得:
根据上述分析得到:在(X1)和(Y2)情形下,ClassⅠ顾客的平均等待时间是相等的,即Wq1x1=Wq1y2.同理可以得到,Wq2x2=Wq2y1,Wq2x3=Wq2y1.
进一步结合(1)~(6)式,可以得到
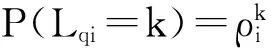
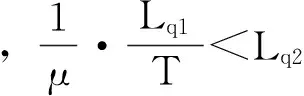
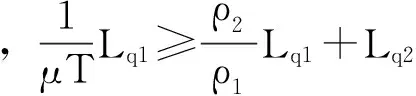
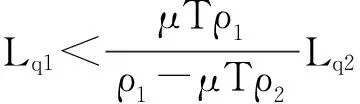
(d)在(Y1)情形下,Lq1≥μTq2,所以,
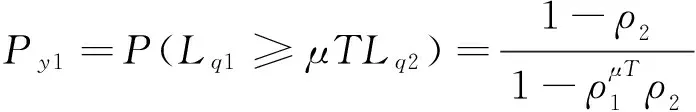
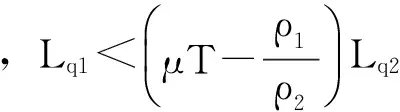
(f)在(Y3)情形下,它的概率与Py1,Py2之和为1,所以,
综上所述,可以得到
2.2待定参数b
上述公式包含唯一的待定参数b,为了进一步确定Wq1,Wq2,以下在三种取值方法下对b值分别加以确定.
1)均值法.假设b在[0,T]上服从均匀分布,则b=T/2.
2)强度法.假设系统中第i等级顾客的服务强度为ρi=λi/μ,则
3)概率法.假设系统的平均最大服务量为μT,则
将上述所有公式代入Wq1,Wq2中,即可得到相应的平均等待时间.
2.3平均逗留时间及队长
顾客在系统中的平均逗留时间等于平均等待时间与平均服务时间之和.令Wi表示第i级顾客的平均逗留时间,i=1,2,则
根据Little公式[1],可以得到ClassⅠ和ClassⅡ顾客的平均等待队长分别为:
3 仿真结果
为了验证b的三种取值方法哪种更加合理,用Matlab对b的相关函数即ClassⅠ和ClassⅡ顾客的平均等待时间Wq1,Wq2进行仿真模拟,其中λ1=1,λ2=2,T=5,μ分别取值5,8,10,结果见表1.

表1 当λ1=1,λ2=2,T=5,μ取不同值时的平均等待时间

(a)λ1=1,λ2=2,T=25

(b)λ1=1,λ2=2,T=100
由表1结果可知,三种取值方法中,概率法条件下的Wq1,Wq2与仿真结果最为接近,说明概率法最符合真实情况.
对比本文所介绍的新的优先权模型和传统的抢占型优先权模型发现,当T变大的时候,两个模型越来越相似.为了证明T型非抢占优先权M/M/1排队系统优于抢占优先权M/M/1排队系统,将T放大,分别取值25,100,进行ClassⅡ顾客平均等待时间的仿真模拟,结果见图4.
从图4可以发现,当T变大时,ClassⅡ顾客的平均等待时间也在变大,这说明模型变为抢占性优先权排队模型时,ClassⅡ顾客的平均等待时间比本文介绍的T型非抢占优先权M/M/1排队系统要大,这会使得系统中的ClassⅡ顾客对于服务效率感到不满,而在实际的认知无线网络频谱选择中,也会造成次用户的频谱选择效率低下.
4 结论
在分析T型非抢占优先权M/M/1排队系统时,计算了相应的平均等待时间、平均逗留时间、平均队长,并通过平均等待时间与仿真结果的对比,得到假设的三种取值方法当中,概率法为b取值的最优方法.T型非抢占优先权M/M/1排队系统与抢占优先权M/M/1排队系统的对比表明,T型非抢占优先权M/M/1排队系统更加合理,更有利于优化服务系统.
[1]齐永.试论认知无线网络中频谱接入技术[J].电子技术与软件工程,2014(19):42.
[2]唐应辉,唐小我.排队论——基础与分析技术[M].北京:科学出版社,2006.
[3]李杰.基于具有强插优先级的M/M/1型排队系统网络延迟分析[J].电子商务,2013(4):314.
[4]张宏波,史定华.M/M/1抢占优先权排队平稳指标的尾部分析[J].系统科学与数学,2014,34(1):1.
[5]KIM K.T-preemptive priority queue and its application to the analysis of an opportunistic spectrum access in cognitive radio networks[J].Computers and Operations Research,2012,39(7):1394.
[6]黄业文,吴红,王远世.非抢占有限优先权M/M/1排队系统[J].计算机工程与应用,2013,49(13):80.
(责任编辑马宇鸿)
M/M/1 queueing system with T-non-preemptive priority
MA Zhan-you,ZHANG Shi-jiu,XU Biao
(College of Science,Yanshan University,Qinhuangdao 066004,Hebei,China)
To optimize a spectrum access in cognitive radio network,a new priority discipline is proposed,which called T-non-preemptive priority discipline,T is a time parameter.T-non-preemptive priority discipline in an M/M/1 queueing system is studied,and then the average waiting time,the average dwell time and the average queue length are obtained while customers stay in the queueing system.Finally,the average waiting time with respect to different parameters is simulated by aid of Matlab software.
M/M/1 queueing system;priority;T-non-preemptive priority;cognitive radio network
10.16783/j.cnki.nwnuz.2016.02.007
2015-06-15;修改稿收到日期:2015-07-17
国家自然科学基金资助项目(61472341);河北省自然科学基金资助项目(A2014203096,G2013203169);燕山大学青年教师自主研究计划项目(13LGA017)
马占友(1974—),男,吉林松原人,教授,硕士研究生导师.主要研究方向为排队论及网络性能分析.
E-mail:mzhy55@ysu.edu.cn
O 226
A
1001-988Ⅹ(2016)02-0029-05
