基于ELVIS的倒立摆二次型最优控制实验系统设计

费红姿, 王纪方, 董　全, 郭新莲, 宋恩哲

(1. 哈尔滨工程大学 动力与能源工程学院, 黑龙江 哈尔滨　150001；2. 重庆红江机械责任有限公司, 重庆　402162)



基于ELVIS的倒立摆二次型最优控制实验系统设计

费红姿1, 王纪方2, 董全1, 郭新莲1, 宋恩哲1

(1. 哈尔滨工程大学 动力与能源工程学院, 黑龙江 哈尔滨150001；2. 重庆红江机械责任有限公司, 重庆402162)

基于NI-ELVISⅡ虚拟仪器实验平台设计开发了倒立摆平衡控制实验系统。首先分析了倒立摆的控制原理,建立了倒立摆控制系统的数学模型,设计了二次型最优控制器；然后在LabVIEW环境中,设计了倒立摆平衡控制实验的前面板,并进行了仿真和实验研究。实验结果表明:该倒立摆实验系统具有良好的创新性,利用此系统学生可以自行开发不同的控制方法,从而激发学生学习控制理论的兴趣,调动学生的主动性,进一步提高实验教学质量。

虚拟仪器; 倒立摆； ELVIS; 二次型最优控制

倒立摆控制实验是“现代控制理论”课程的典型实验项目。倒立摆是一个非线性、多变量、不稳定系统,能直观地表现出许多抽象的控制概念,如系统稳定性、可控性、系统收敛速度与抗干扰能力等,是进行控制理论教学及开展各种控制实验的理想实验平台[1-2]。传统的倒立摆实验系统通常由倒立摆组件、驱动器、电机和控制器等构成,其特点是硬件电子线路和系统软件固定,学生在实验过程中按照设定的步骤完成实验,这种方式不利于培养学生自行设计能力。另外，传统的系统可扩展性较差[3-5]。

虚拟仪器是近年来发展起来的仪器与计算机相结合的产物,具有可扩展好、集成度高、在线编程方便等优点,可为用户提供广阔的发挥空间[6-8]。ELVIS是NI公司推出的虚拟仪器教学平台,基于此平台开展测控类课程的开放式实验教学,可以给予学生更大的发挥空间,有利于教学内容的不断更新,为学科发展提供支撑。本文研究的单级倒立摆模块是Quanser公司开发的组件,在ELVISⅡ虚拟仪器平台上可以对该倒立摆模块的控制系统进行二次开发和设计。

本文构建了基于ELVISⅡ虚拟仪器实验平台的倒立摆控制实验系统,建立了倒立摆的状态空间模型,设计了二次型最优控制器,开发了倒立摆实验系统软件,进行了倒立摆的平衡控制实验研究。

1　基于ELVISⅡ的倒立摆实验平台

1.1ELVISⅡ简介

ELVISⅡ虚拟仪器教学实验套件是为课堂或实验室服务的先进教学平台,可以进行电路设计、仪器控制、嵌入式/单片机等课程的理论教学[9-10]。ELVISⅡ原型实验板具有很好的通用性,通过外部接口金手指插槽可以连接不同的功能模块,也可以根据需要自行设计功能模块,并在LabVIEW软件环境下编写相应的程序完成的数据采集、控制、保存、分析和显示功能,平台如图1所示。

图1　NI-ELVIS虚拟仪器平台

1.2倒立摆控制模块

倒立摆控制模块如图2所示,它由直流电机、编码器、旋转臂、摆杆和质量块等组成,通过金手指连接端子连接在ELVISⅡ虚拟仪器实验平台上。

图2　倒立摆控制模块

倒立摆控制系统结构如图3所示。倒立摆系统的旋转臂通过电机驱动在水平面上旋转,带动摆杆在平衡位置来回振荡,从而使摆杆稳定在竖直向上的某个位置上。系统中的2个光电编码器分别测量旋转臂的转动角度θ和摆杆的摆动角度α,编码器与ELVISⅡ上的数据采集单元相连,采集得到的旋转臂和摆杆转过的角度输送给控制器,控制器的输出作为电机驱动电路的输入,控制旋转臂转动的角度和方向,形成闭环系统。

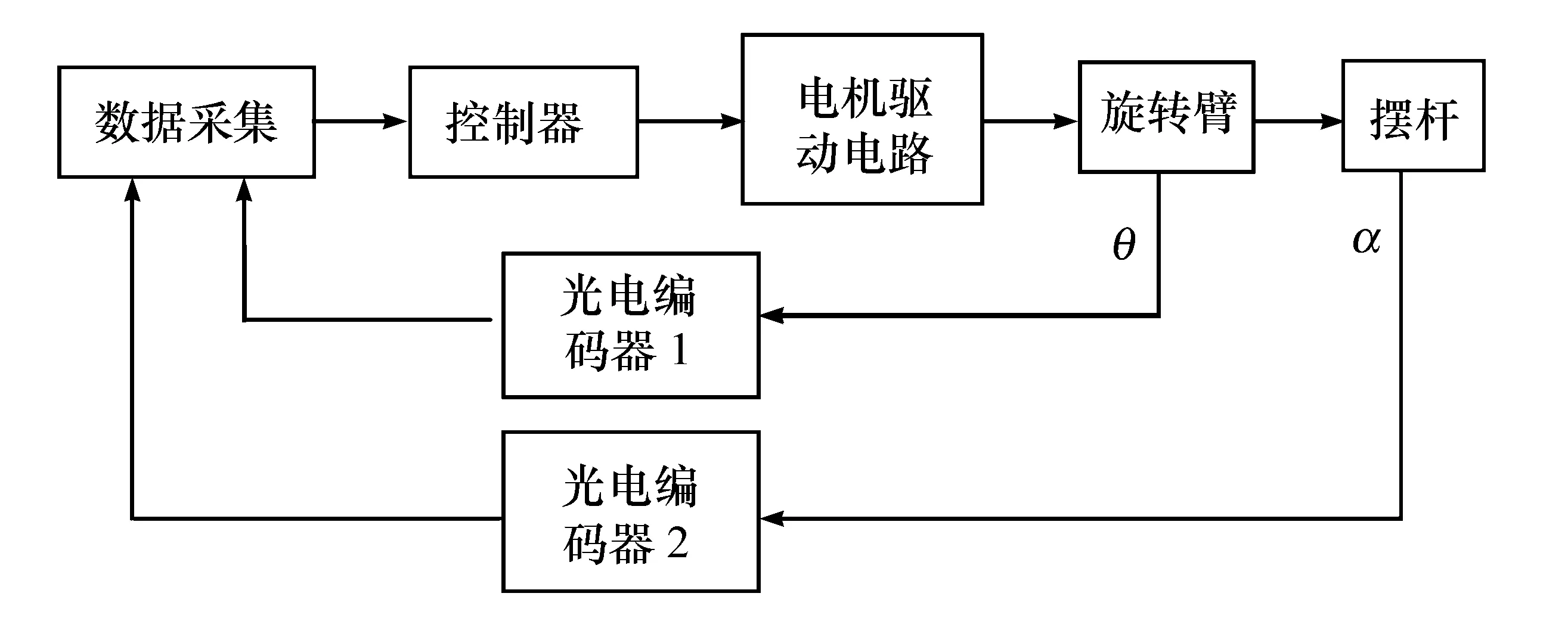
图3　倒立摆控制系统结构图

2　倒立摆数学模型

对倒立摆的结构及其运动进行分析,可简化成如图4所示的模型。倒立摆模块有两个方向上的旋转运动,摆杆及旋转臂随着电机轴在水平面内做旋转运动,同时摆杆绕摆转轴在竖直平面内做旋转运动[11-12]。

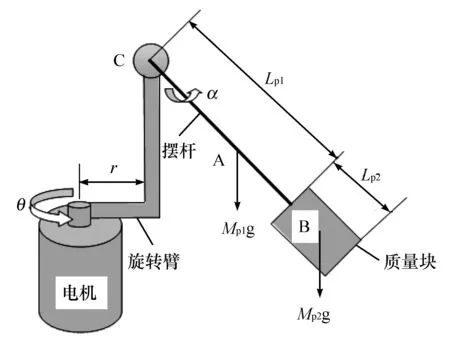
图4　倒立摆结构简化模型

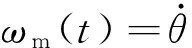
(1)

式中Km、Kt是与电机自身系统有关的系数, u(t)为电机的输入电压。

电机带动旋转臂运动,可得

(2)

式中,Je电机轴和负载的转动惯量,I为电机产生的力矩,N为阻力(水平方向),r为摆杆到轴心的距离。

将摆杆的运动结构单独取出进行受力分析并在摆杆转轴中心建立坐标系,如图5所示。

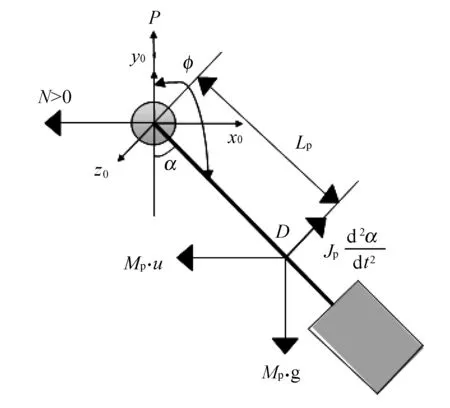
图5　摆杆的受力分析

图5中：D为等效重心；P为竖直向上的受力；N为水平方向的受力；Lp为等效重心到转轴的距离；Mp为摆杆与质量模块总质量；x0y0z0为坐标系；u为电机的输入电压。

假定摆杆和质量块都是匀质的,通过结构受力分析,得到等效重心到转轴的距离Lp为

(3)

式中,Lp1为摆杆长度,Lp2为质量块长度,Mp1为摆杆质量,Mp2为质量块的质量。

在竖直方向上对摆杆进行受力分析,得到:

(4)

此时,Mp=Mp1+Mp2,即

(5)

在水平的切向方向上对摆杆进行受力分析,得到:

(6)

即:

(7)

由摆杆的运动分析,得到:

(8)

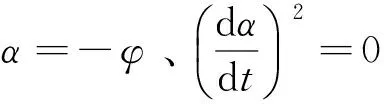
(9)

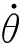
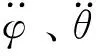
(10)

式中,Rm为电机电阻,Kt为电机扭矩常数,Km为电机反向感应常数。代入实际参数,可得:

(11)

3　最优控制器设计

3.1最优控制器设计

假设线性定常系统:

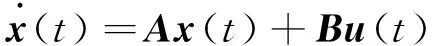
(12)

式中:x(t)为n维状态矢量；u(t)为m维控制矢量；A和B分别是n×n、n×m维常数矩阵。系统的性能指标可以表示为:

(13)

式中:Q是n×n维常数对称正定矩阵；R是m×m维常数对称正定矩阵,Q和R分别是对状态变量、控制输入的加权矩阵。根据最优控制算法,使性能指标J极小的最优控制u*(t)为

(14)

式中:G为m×n维常数矩阵,称为反馈增益矩阵； K为n×n维正定对称矩阵,是黎卡提代数方程的解:

-KA-ATK+KBR-1BTK-Q=0

(15)

根据期望性能指标选定加权矩阵Q和R,根据公式(15)得到最优控制矩阵K,此时控制量为

u=-Gx=-(g1x1+g2x2+g3x3+g4x4)

(16)

3.2仿真研究

Q用来设定性能指标中状态变量之间的权重。Q1,1是对电机旋转角度变量的加权。增加Q1,1在最优控制函数中的权重,可以使动态响应加快,上升时间变短,经过多次试验选取Q1,1=20,利用式(15)求得控制参数(反馈增益矩阵):

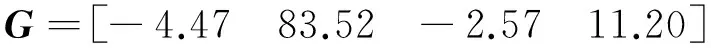
系统响应仿真曲线见图6和图7。此时,摆杆转角响应的上升时间为1.3 s,超调量10%。

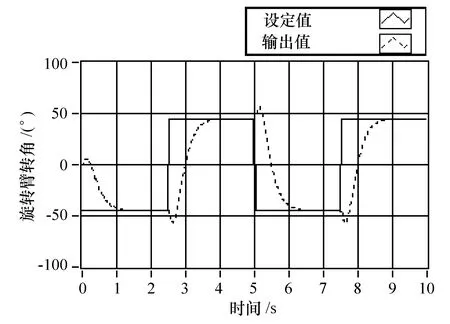
图6　旋转臂的阶跃响应曲线

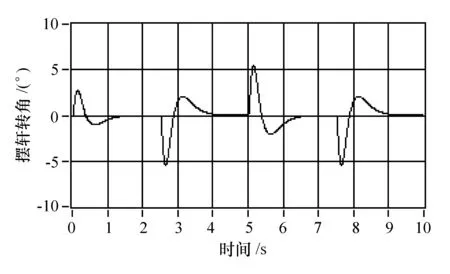
图7　摆杆偏离平衡位置的角度曲线

4　实验研究

4.1控制系统前面板设计

倒立摆控制模块的虚拟仪器面板如图8所示。该控制系统可以实现摆杆的平衡控制和自动起摆控制,在前面板上,有平衡控制器参数模块、自动起摆控制器参数模块、电机参数模块等,可以对相应模块的具体参数进行设置或修改,同时可以显示摆杆位置、电机电压,及摆杆和旋转臂的角度曲线。

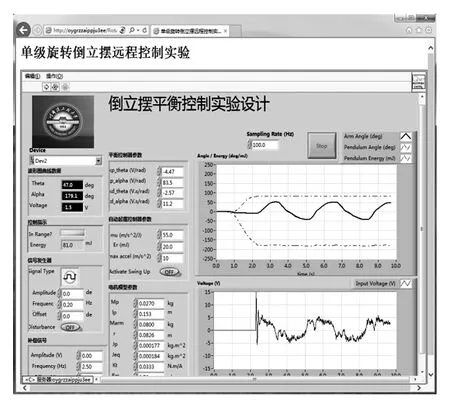
图8　倒立摆控制模块

4.2平衡控制实验

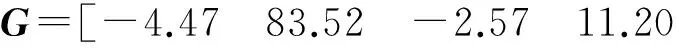
从实验结果可以看出,在摆杆被竖起的最开始阶段,旋转臂的振荡幅度不均匀,经过很短一段时间后,旋转臂可以达到目标位置,并且同时使摆杆稳定在平衡位置附近。为保持摆杆稳定,旋转臂在平衡位置附近来回振荡。

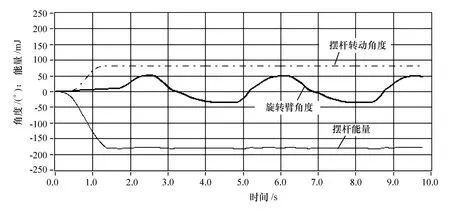
图9　平衡控制实验曲线

当摆杆稳定在平衡位置时,在一个小范围内,给摆杆一定的扰动,旋转臂经过振荡又回到原来的动态平衡位置。图10所示为干扰作用下的系统响应曲线。从图中可以看出摆杆在控制器的作用下通过改变旋转臂和摆杆的转动角度,使摆杆快速回到竖直向上的平衡位置。图11为倒立摆控制实验照片。

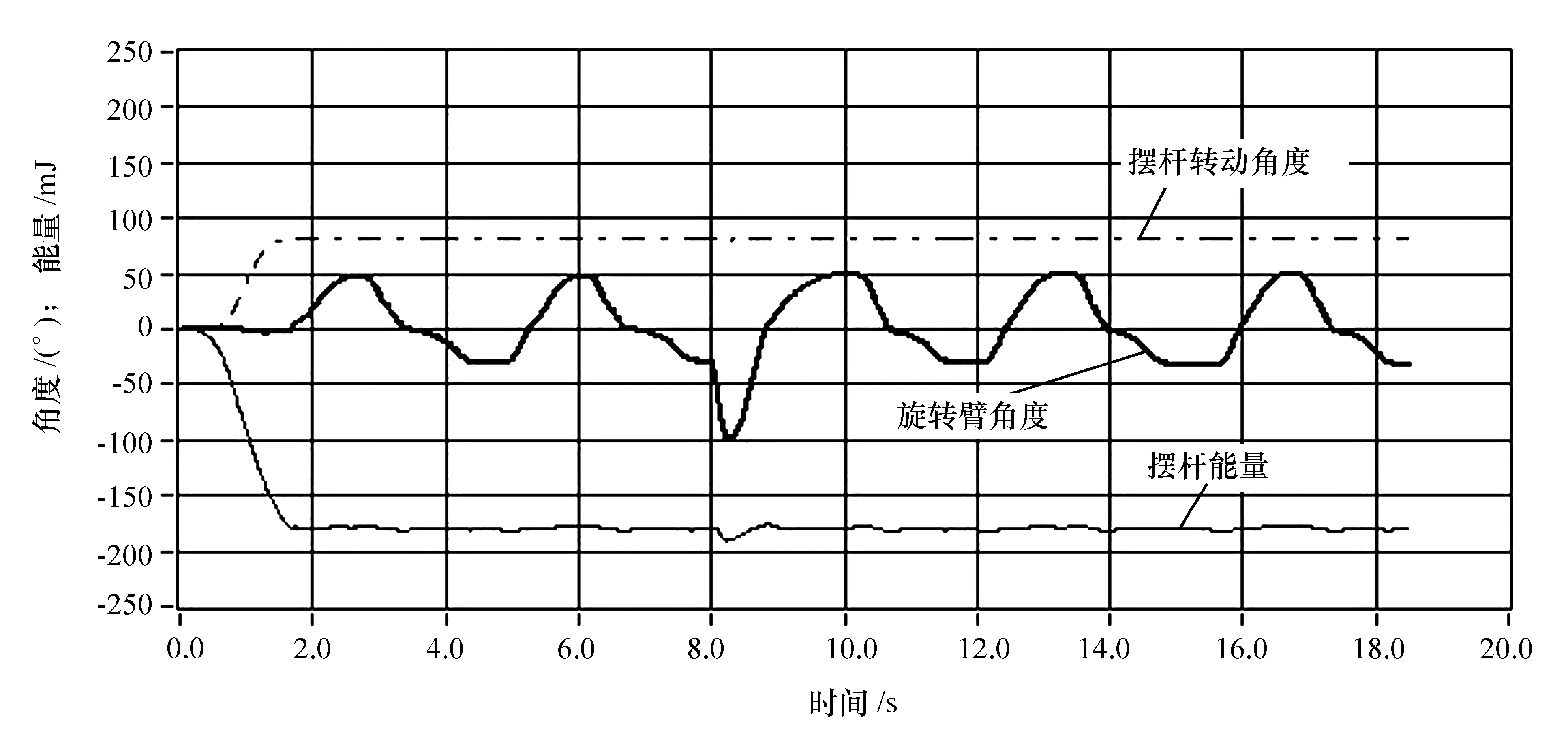
图10　摆杆受到扰动后的平衡曲线

图11　倒立摆控制实验照片

5　结论

本文基于ELVISⅡ虚拟仪器平台和倒立摆控制模块设计开发了倒立摆控制实验系统,建立了倒立摆的数学模型,设计了二次型最优控制,并进行了倒立摆平衡位置控制和干扰控制实验研究和验证,取得了较好的实验效果。

基于ELVISⅡ虚拟仪器的倒立摆实验系统将原来单一的验证性实验模式改成开放式的实验模式,为学生提供一个开放式的软件及硬件平台。实验结果表明,该系统可以作为现代控制理论实验平台,学生可以在此平台上自行设计实验方式和控制方法,该系统可以更好地激发学生学习的兴趣,帮助学生深入理解所学的理论知识。

References)

[1] 刘浩梅, 张昌凡. 基于LQR的环形单级倒立摆稳定控制及实现[J].中南大学学报:自然科学版,2012,46(9): 3496-3501.

[2] 张永立, 李洪兴, 苗志宏, 等. 基于变增益LQR控制方法的二级倒立摆自动摆起[J].系统工程理论与实践,2011,31(7):1341-1355.

[3] 张华宾, 张培仁, 李昊华, 等. 基于DSP的两轮式倒立摆自平衡控制系统[J].测控技术,2007,26(11):23-26.

[4] 罗晶, 陈平.一阶倒立摆的PID控制[J].实验室研究与探索,2005,24(11):26-28.

[5] 许谨,齐胜男,胡立夫,等. 基于倒立摆的综合性实验设计[J].实验室科学,2013,16(3):7-10.

[6] 全晓莉,周南权. 基于虚拟仪器技术的数字电路实验系统研究[J].实验技术与管理,2014,31(4):96-98.

[7] 詹惠琴,古军. 虚拟仪器课程实验建设与改革[J].实验技术与管理,2014,31(7):94-96.

[8] 李欣,谢宏. 虚拟仪器技术在通信原理教学中的应用[J].实验室研究与探索,2014,33(5):155-159.

[9] 徐苒,金暄宏,戴曙光.基于NI ELVIS II的温度采集系统设计[J].仪表技术,2010(2):33-35.

[10] 胡继康,陈永志,周求湛,等. 基于NI ELVIS 的网络化实验教学平台[J].实验室研究与探索,2012,31(5):154-157.

[11] 张蛟龙, 宋运忠. 基于LQR的平面二级倒立摆控制策略研究[J]. 自动化技术与应用,2009(12):1-4.

[12] 段学超. 平面倒立摆的建模、控制与实验研究[D].西安:西安电子科技大学,2006.

Design of inverted-pendulum experimental system using LQR method based on ELVIS

Fei Hongzi1, Wang Jifang2, Dong Quan1, Guo Xinlian1,Song Enzhe1

(1. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China;2. Chongqing Hongjiang Machinery Co., LTD, Chongqing 402162, China)

The inverted-pendulum experimental system using LQR method is designed and developed based on NI-ELVISⅡvirtual instrument platform. First, the control principle of the inverted-pendulum is analyzed and the model of control system is built. Then the LQR controller is designed. The front panel for experimental system is programmed using LabVIEW. And simulation and experimental study on this system are all produced in detail. The experimental results prove that the ELVIS experimental platform is more innovative than traditional devices and methods, and the students can implement more creative experiments on it. Thus the interests and activities of students can be aroused greatly, and it is helpful to improve the teaching quality.

virtual instrument; inverted-pendulum; ELVIS; LQR

10.16791/j.cnki.sjg.2016.03.019

2015- 08- 26修改日期:2015- 10- 17

黑龙江省自然科学基金项目(E2015049);哈尔滨工程大学教育教学改革研究项目(JB2013YB11)

费红姿(1970— ) , 女,上海,博士,副教授,研究方向为动力装置控制与测试技术.

E-mail:fhz@ hrbeu. edu.cn

TP273；G484

A

1002-4956(2016)3- 0070- 05