索赔服从伽马分布的经典风险模型的破产概率

高嘉卉，王秀莲

（天津师范大学数学科学学院，天津300387）

索赔服从伽马分布的经典风险模型的破产概率

高嘉卉，王秀莲

（天津师范大学数学科学学院，天津300387）

针对连续时间的经典风险模型，当索赔变量服从伽马分布时，根据对Lundberg基本方程的求解，得到了罚金函数为指数形式的期望贴现罚金函数的表达式，从而得出了相应的破产概率.

经典风险模型；伽马分布；罚金函数；Lundberg基本方程；破产概率；期望贴现罚金函数

对于连续时间的经典风险模型，保险公司的盈余｛U（t），t≥0｝为

其中：U（0）=u为公司的初始盈余；c＞0为常数，表示保险公司单位时间内收到的保费；Xj是保险公司的第i次索赔额，｛Xj，j=1，2，…｝为独立同分布的非负随机变量，分布函数为P（x），密度函数为p（x）；｛N（t），t≥0｝是参数为λ＞0的Poisson过程，表示到时刻t为止的索赔次数.｛Xj，j=1，2，…｝和｛N（t），t≥0｝相互独立.

假设T为破产时间，T=inf｛t|U（t）＜0｝（当破产没有发生时T=∞），最终破产概率是一个初始盈余U（0）=u≥0的函数

设随机变量U（T-）表示破产前盈余，U（T）表示破产盈余，取ω（x，y）为定义在x＞0、y＞0的非负函数，则u＞0时的期望贴现罚金函数φ（u）可以表示为

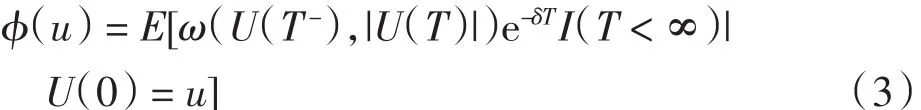
其中δ＞0是折现利息率.

显然，若取ω=1，δ=0，则φ（u）=ψ（u）.令β＞0，定义函数Ф（u），

则当ω（x，y）=e-βy时，Ф（u）=φ（u）.

对于经典风险模型问题，许多学者从不同的角度得到了许多结果.文献［1］给出了ψ（u）所满足的更新方程，研究了经典模型的破产概率，得出索赔服从指数分布和混合指数分布的破产概率.文献［2］在马氏调节环境下给出了索赔服从泊松分布的贴现罚金函数满足的积分微分方程，并计算了初值u=0对应的函数值φ（0）.文献［3］将时间按观察时刻离散化后，给出了贴现罚金函数满足的积分微分方程，并在指数索赔情况下进行了进一步求解.文献［4］研究线性红利边界下两步保费率风险模型的Gerber-Shiu贴现罚金函数，同时给出了线性红利边界下Lundberg基本方程.文献［5］针对2类更新风险模型，利用Laplace变换求出了最终破产概率，并研究了相应的期望贴现罚金函数.伽马分布在保险和经济数据分析中应用非常广泛，是用来拟合理赔额的重要分布［6］.本研究选取指数形式的罚金函数，基于对Lundberg基本方程的求解，推导出索赔变量服从伽马分布时的期望贴现罚金函数的表达式，从而得出了相应的破产概率.

1 Ф（u）的表达式

取φρ（u）=e-ρuφ（u），φρ（u）满足的方程为

定义

则l（ρ）为式（5）中φρ（u）的系数.考虑等式

式（7）是Lundberg基本方程，设ρ是Lundberg基本方程的非负解，则有

对式（8）从u=0到u=z积分，并乘以eρ z，则函数φ（u）满足更新方程

令

当ω（x，y）=e-ρy时，有

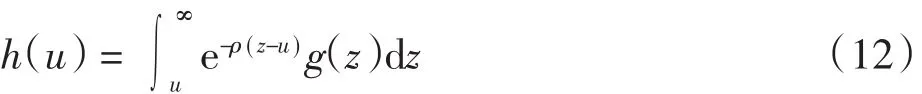
由式（4）可知

对式（13）进行Laplace变换，得

这里

将式（15）代入式（14），化简得

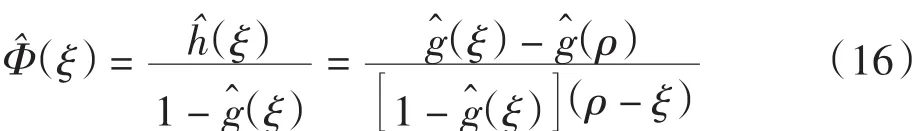
设-r1，-r2，…，-rm是gˆ（ξ）=1的m个不同的根，n1，n2，…，nm为根的重数，由Heaviside扩张公式［7］得

当n1=n2=…=nm=1时，可得Ф（u）的简式为

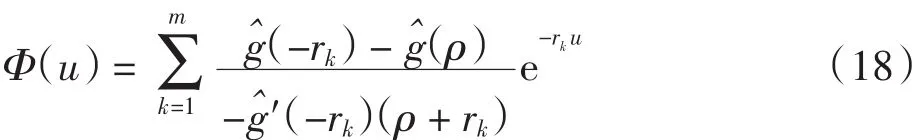
由式（10）可知

则有

令u=0可得1-Ф（0），最终得到

2 索赔为伽马分布的破产概率

设索赔的密度函数为

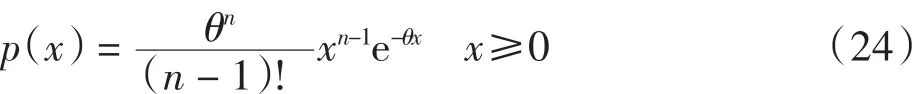
2.1 Lundberg基本方程的解

p（x）的Laplace变换为

由Lundberg基本方程可得

式（26）的非负值解ρ是Фˆ（ξ）的奇点.设

对f（ξ）求导，有

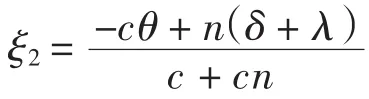
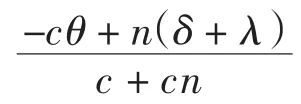
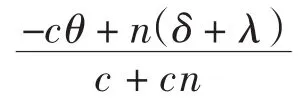
时，f′（ξ）＜0.

显然f（ξ）是连续函数，计算得

（1）若n为奇数，由单调性分析知方程有1个负值解，设这个解为-r0，则有0＜r0＜θ.

（2）若n为偶数，令ξ=-θ-q，其中q＞0，则有

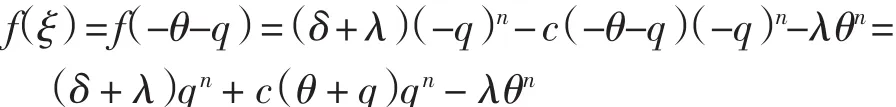
当q足够大时，f（ξ）＞0，方程有2个负值解，设这2个解为-r1、-r2，则有0＜r1＜θ＜r2.

2.2 破产概率

由式（25）有

（1）当n为奇数时，方程的解为-r0，此解为m0重，由式（23），Ф（u）的简式为

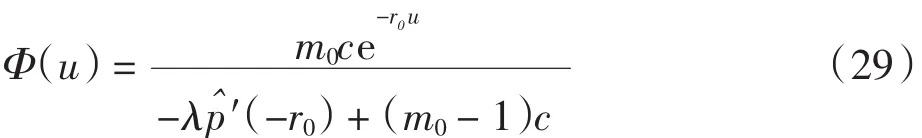
（2）当n为偶数时，方程的解为-r1、-r2，其重数分别为m1、m2，由式（23），Ф（u）的简式为

另一方面，由式（10）可得

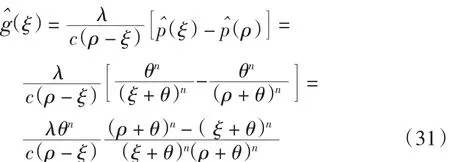
由于

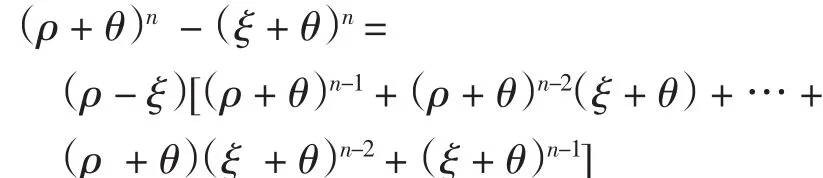
故有

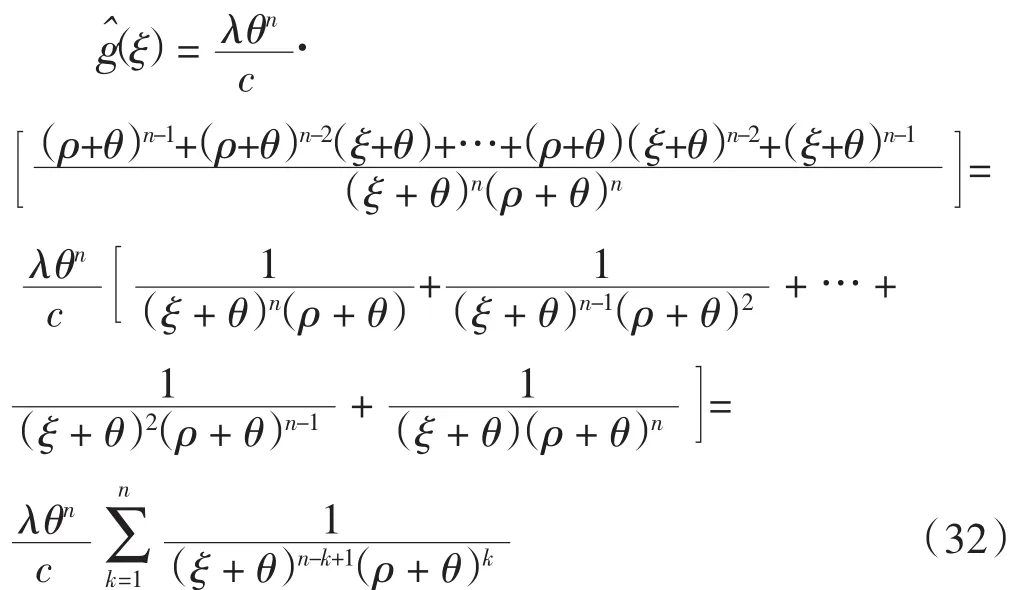
代入ξ=ρ，得到

由式（13）、式（32）和式（33）得到

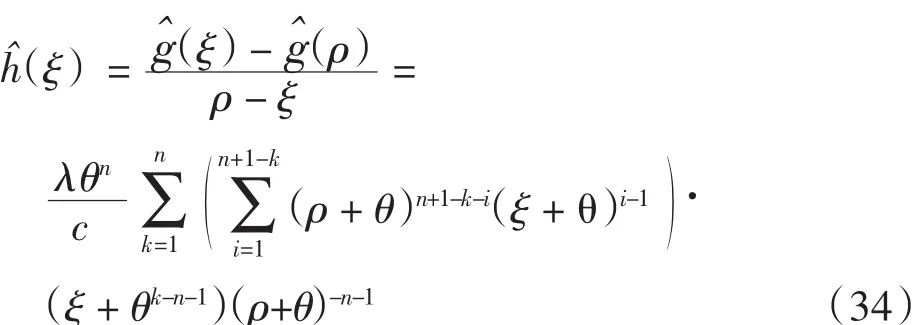
对式（31）求导可得

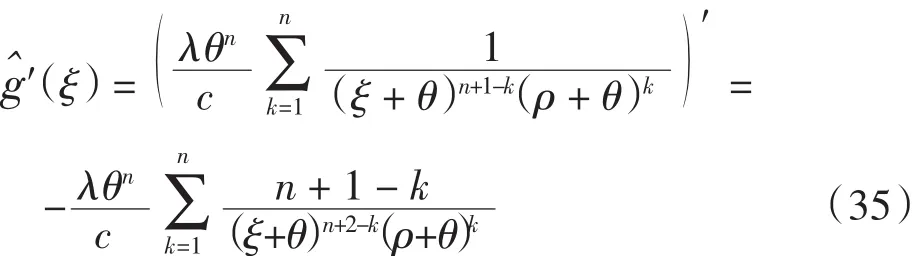
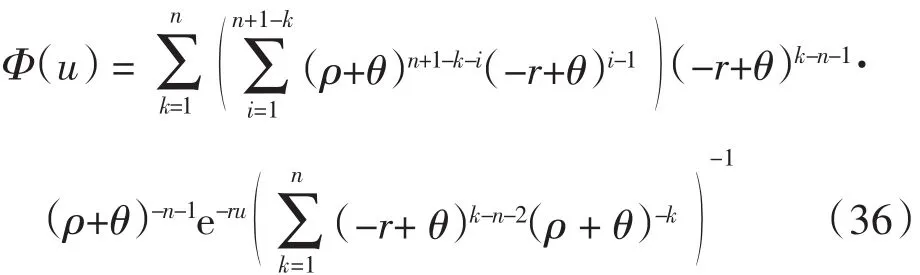
式（29）、式（30）与式（36）均为破产概率，它们在数值上是相等的.特别地，当n=1时，伽马分布是参数为λ的指数分布，因此

当索赔服从指数分布时，有

由式（4）Ф（u）的拓展意义，可得当u≥0时，有

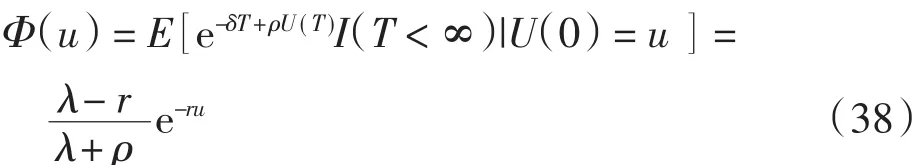
这个结果与式（37）相同.

［1］GERBER H U，SHIU E S W.On the time value of ruin［J］.North American Actuarial Journal，1998，2（3）：48-78.

［2］ZHANG X.On the ruin problem in a Markov-modulated risk model［J］.Methodol Comput Appl Probab，2008，10：225-238.

［3］HANSJORG A.Randomized observation periods for the compound Poisson risk model：The discounted penalty function［J］.Scandinavian Actuarial Journal，2010（1）：1-29

［4］杨莉，孙浩，田兴虎.线性边界下两步保费率风险模型的Gerber-Shiu罚金函数［J］.数学的实践与认识.2007，37（11）：58-67.YANG L，SUN H，TIAN X H.On the discounted penalty function in a two-step premium rate model with linear dividend barrier［J］.Mathematics in Practice and Theory，2007，37（11）：58-67（in Chinese）.

［5］赵永霞.若干风险模型中期望折现罚金函数和最优分红的研究［D］.上海：华东师范大学，2014.ZHAO Y X.Research on the Expected Discounted Penalty Function and the Optimal Dividend in Some Risk Models［D］.Shanghai：East China No-rmal University，2014（in Chinese）.

［6］王丙参，魏艳华.伽玛分布的优良特性及其在风险管理中的应用［J］.宁夏师范学院学报，2010，31（6）：21-24.WANG B C，WEI Y H.Properties of Gamma distribution and its applications to risk management［J］.Journal of Ningxia Teachers University：Natural Science，2010，31（6）：21-24（in Chinese）.

［7］于慎根，杨永发，张相梅.复变函数与积分变换［M］.天津：南开大学出版社，2006.YU S G，YANG Y F，ZHANG X M.Complex Variables Functions and Integral Transformation［M］.Tianjin：Press of Nankai University，2006 （in Chinese）.

（责任编校 马新光）

Ruin probability with Gamma claim in classical risk model

GAO Jiahui，WANG Xiulian
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

For the classical risk model of continuous time，the expression of expected discounted penalty function is given on the basis of Lundberg＇s Fundamental equation，when the penalty function is certain exponential form and claim variable is Gamma distribution.The ruin probability is obtained correspondingly.

classical risk model；Gamma distribution；penalty function；Lundberg＇s Fundamental equation；ruin probability；expected discounted penalty function

O211.67

A

1671-1114（2016）03-0013-03

2015-09-26

国家自然科学基金资助项目（11401436）.

高嘉卉（1990—），女，硕士研究生.

王秀莲（1965—），女，副教授，主要从事概率统计及其应用方面的研究.