单轴应变下CaO和SrO电子结构和光学性质的第一性原理研究

邢美静，梁 凯，姚倩倩，李 实，申 洁，赵 辉

（天津师范大学物理与材料科学学院，天津300387）

单轴应变下CaO和SrO电子结构和光学性质的第一性原理研究

邢美静，梁 凯，姚倩倩，李 实，申 洁，赵 辉

（天津师范大学物理与材料科学学院，天津300387）

为探究不同单轴应变条件对碱土金属氧化物CaO和SrO晶体材料电子结构和光学性质的影响，采用第一性原理计算方法，利用密度泛函近似理论，对晶体的能带结构、态密度和介电函数进行计算，并利用克喇末-克朗尼格关系得出晶体的光学常数.研究结果表明：无应变时，CaO和SrO晶体是宽禁带且具有直接带隙的绝缘体，施加单轴应变使晶体带隙的宽度变窄，导电性能增强，且单轴压应变对晶体电子结构的影响比拉应变对晶体电子结构影响明显.2种晶体均为各向同性材料，单轴拉应变使静介电常数变大，单轴压应变使静介电常数变小.光子能量在0～15eV时，2种材料折射率、吸收系数和反射率等光学谱的峰位和峰值均受单轴应变的影响较大，单轴拉应变使得各光学谱的峰位向能量低的方向移动，峰值升高；单轴压应变使得光学谱的峰位向能量高的方向移动，峰值降低.同时单轴拉应变使晶体静态介电常数和静折射率增大，压应变使之降低.研究表明单轴应变可以有效调节CaO和SrO的电子结构和光学性质.

CaO晶体；SrO晶体；第一性原理；单轴拉应变；单轴压应变；电子结构；光学性质

金属氧化物是一类在催化作用、微电子和光电设备等领域应用广泛的材料［1-4］，其中碱土金属氧化物是地球地下幔的重要成分，是一种广泛应用的工业科学技术基础材料［5-8］.CaO是一种宽带隙的氧化物，可用于漂白和自动加热包等方面；SrO可应用于燃料电池，根据它的光学性质，SrO还可以用来提高特殊玻璃的质量［9］.2种材料均为宽带隙金属氧化物，在实验和理论两方面被广泛研究.CaO在静水压为61 GPa的条件下可以实现从B1（NaCl）相到B2（CsCl）相的转变［10］，且至少在135 GPa条件下才能使B2相处于稳定状态［11］，Kalpana［12］和Baltachea［8］等已对CaO的相变问题进行了具体研究；另一方面Mehl等［13］预测了CaO的弹性性质受压强的影响.与此同时，SrO的弹性性质、热力学性质和相变等问题也有大量研究［2-3，8，14］.

综上所述可知，现有的大部分研究多集中在晶体材料的弹性性质和相变等问题上，部分研究涉及静水压条件下CaO和SrO的光学性，对单轴应变条件下二者的电子结构和光学性质研究较少，本研究基于密度泛函理论的第一性原理，讨论单轴应变条件对CaO和SrO的电子结构和光学性质的影响.

1 计算方法与模型

本研究从第一性原理出发，采用基于密度泛函理论的平面波赝势方法的CASTEP软件包［15-16］进行计算，利用超软赝势［15，17］描述离子势与价电子间的相互作用势，其中Ca和Sr各原子的价电子组态分别为3s23p64s2和4s24p65s2，O原子的电子组态为2 s22 p4.电子交换相关项采用广义梯度近似（GGA）［18］.在倒易空间中，平面波截止能为380.0eV，布里渊区网格［19］选取4×4×4的格点.在对模型结构优化时采用BFGS［20］算法，自洽循环计算收敛精度为每个原子平均能量小于5×10-6eV，原子间的相互作用力低于0.1eV/nm，最大内应力为0.02GPa，原子的最大位移为5×10-5nm.

CaO和SrO属于立方晶系，空间群为Fm-3m，与NaCl晶体结构相似.CaO晶体原子坐标分别为Ca（0，0，0）和O（0.5，0.5，0.5），优化后晶格常数a=b=c=0.4828nm，与其他文献计算值0.4819nm符合良好［21］，且与实验测量值a=b=c=0.481 1 nm非常相近；SrO晶体中的原子坐标分别为Sr（0，0，0）、O（0.5，0.5，0.5），优化后晶格常数a= b=c=0.5190nm，与其他研究计算值0.5181nm和实验值0.516 0 nm［2］基本一致.单轴应变施加在z轴方向，施加单轴应变的晶格常数的相对变化定义为η=（c-c0）/c0×100%，其中c为施加应变后z轴方向晶体的晶格常数，c0为不受应变作用时z轴方向晶体的晶格常数.本研究通过对CaO和SrO施加15%单轴拉应变和-15%的单轴压应变来讨论单轴应变对晶体电子结构和光学性质的影响.

2 计算结果与讨论

2.1 单轴应变对晶体电子结构的影响

优化后未施加单轴应变时，CaO和SrO晶体沿布里渊区对称点方向的能带结构、总态密度和分波态密度如图1所示.

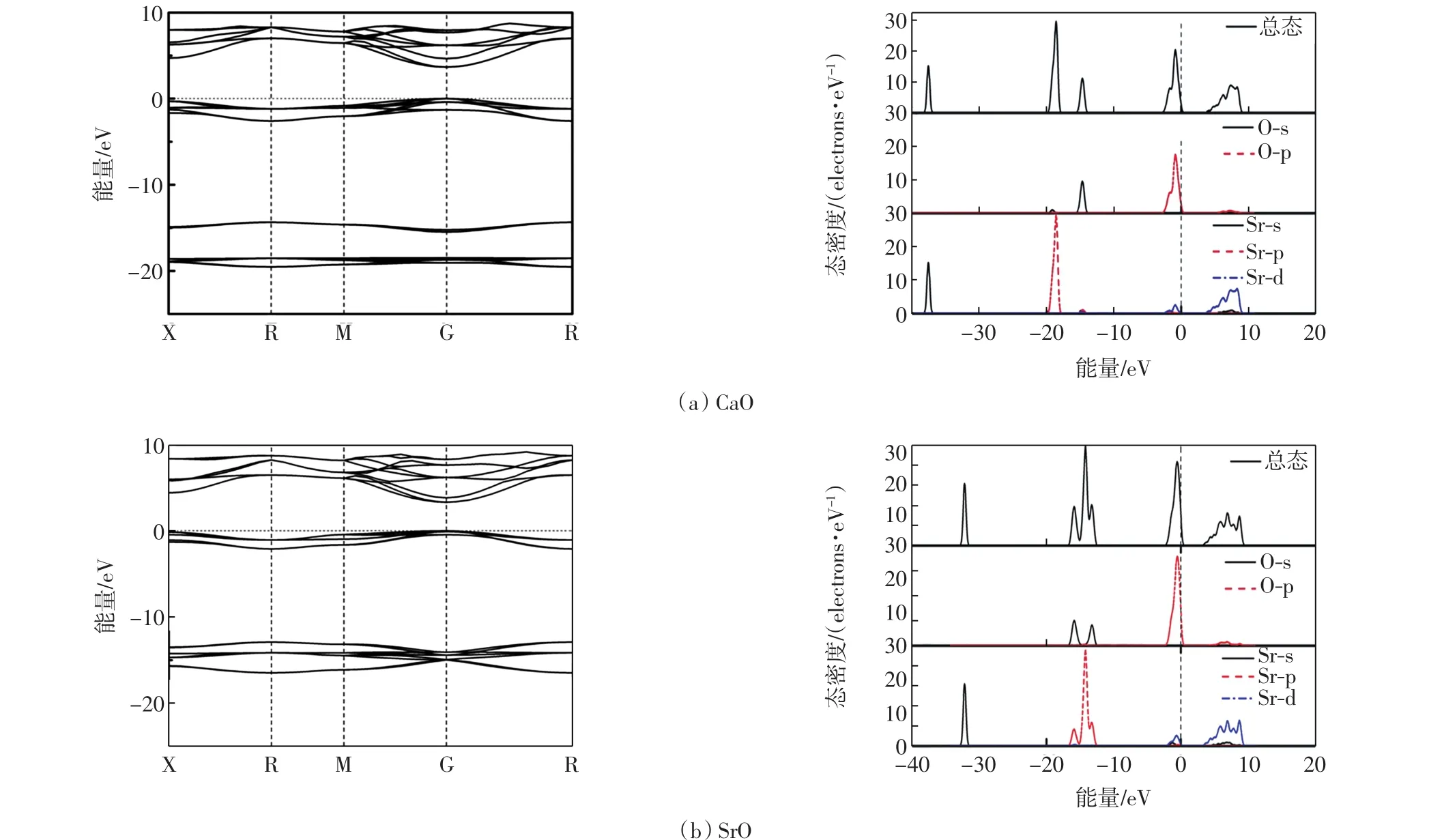
图1 无应变时，CaO和SrO的能带结构图和态密度图Fig.1 Electronic band structure and corresponding DOS of CaO and SrO without strain

由图1（a）可知，在未发生应变的情况下，CaO晶体导带底和价带顶均在布里渊区的G点，带隙宽度为3.658 eV，说明此种材料为直接带隙的绝缘体.该结果与文献［22］中计算的结果相近，但比实验值（7.1 eV）明显偏小，这是因为无论采用广义梯度近似（GGA）还是局域密度近似（LDA）都不能完全描述多电子相互作用，因此均存在禁带宽度计算值偏低的问题，对比图1（b）可知，SrO与CaO的能带结构存在导带底和价带顶均出现在G点的共同点，说明2种材料都是直接带隙的绝缘体（SrO禁带宽度为3.337 eV）.此外，由图1（a）中CaO总态密度和各原子分态密度图可以看出，CaO的价带分为4个部分：-38.53～-36.58 eV处的态密度由Ca的s态贡献；-20.3～-17.45 eV处的峰值主要由Ca 的p态贡献，同时O的s态也有少量贡献；-16.19 eV～-13.37 eV处的峰值主要由O的p态贡献；价带顶部主要由O的p态贡献，并掺杂Ca的d态.导带底部的态密度由Ca的d态贡献，并有少量的O的p态贡献.

施加单轴拉应变和压应变后，CaO和SrO晶体沿布里渊区对称点方向的能带结构和态密度分别如图2和图3所示.

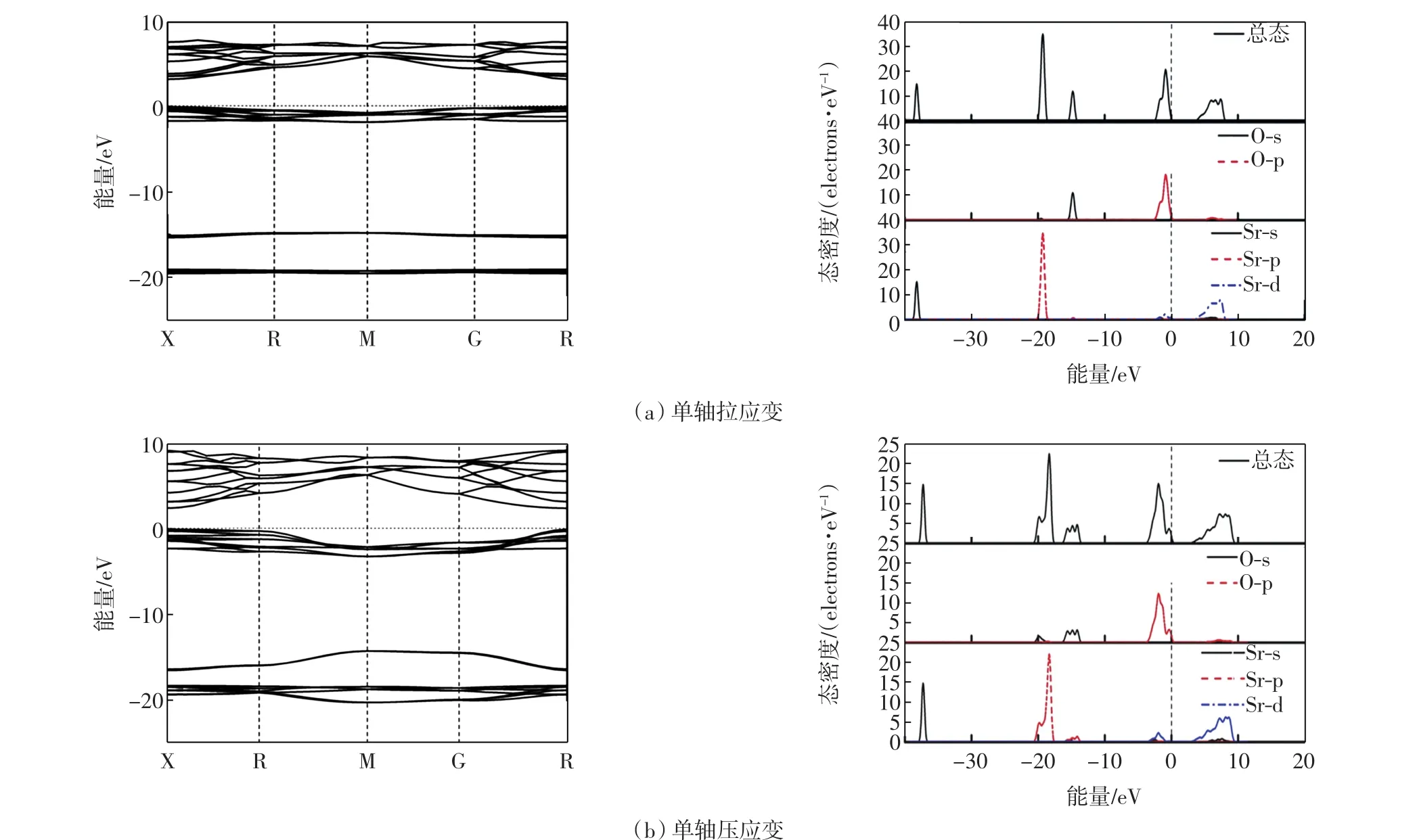
图2 施加应变后，CaO的能带结构图和态密度图Fig.2 Electronic band structure and corresponding DOS of CaO under uniaxial strains

图2（a）和图2（b）分别给出单轴拉应变和单轴压应变条件下，CaO的能带结构和态密度.由能带结构图可以看出，无论是施加拉应变（η=15%）还是施加压应变（η=-15%），导带底和价带顶均转移到X点，仍然是直接带隙.2种条件下，CaO的带隙均变窄，禁带宽度分别减小为3.254 eV和2.474 eV，η=-15%的单轴压应变对带隙宽度的影响明显比η=15%单轴应变影响大.2种应变条件对CaO能带结构的影响不同，单轴拉应变使能带曲线更平滑，单轴压应变使曲线波动起伏更大，能带宽度变宽.由态密度图可以看出，由Ca的d态电子占据的导带底均向低能量方向移动，从而使带隙变窄，这与能带结构的变化一致，因为能带越平，态密度峰值越尖锐，由于拉应变使能带曲线变得更加平缓，所以η=15%单轴拉应变情况下，CaO态密度的峰值升高；而η=-15%单轴压应变条件下CaO态密度的峰值降低；且在η=-15%单轴压应变条件下CaO态密度所在区域变大，造成体系离域性增强，这与单轴压应变条件下能带变宽一致.

对比图3（a）和图3（b）中SrO在15%单轴拉应变和-15%单轴压应变条件下的电子结构可以发现，SrO 和CaO电子能带结构和态密度的变化趋势基本相同，如单轴应变条件下SrO还是直接带隙，其导带底和价带顶均出现在X点.区别是单轴应变对SrO晶体带隙影响比较明显，单轴拉应变和压应变的带隙分别为件下晶体的导电性有所增强.2.645 eV和1.697 eV.由态密度图（图3（b））可知，SrO价带顶的电子在压应变条件下向能量高的方向移动，跨越费米面，这是O的p态电子向高能量方向移动造成的.此外，SrO态密度图的变化说明在单轴压应变条

图3 施加应变后，SrO的能带结构图和态密度图Fig.3 Electronic band structure and corresponding DOS of SrO under different uniaxial strains

2.2 单轴应变对晶体光学性质的影响

在线性光学响应范围内，通常用复介电函数

描述固体宏观光学响应函数，式（1）中：ε1（ω）为介电实部，ε2（ω）为介电虚部［22］.复介电函数ε（ω）与电子和光子的相互作用密切相关，是连接固体材料微观电子结构和宏观光学性质的桥梁，通过ε（ω）可以方便地得到其他各种光谱信息.介电函数虚部ε2（ω）主要表征电子占有态与非占有态间的跃迁，通过占据态和非占据态波函数的动量矩阵元可得介电函数的虚部ε2（ω），再根据克喇末-克朗尼格（Kramer-Kronig）色散关系，由ε2（ω）可以得到介电函数的实部［23-24］.ε1（ω）和ε2（ω）的表示方法分别为

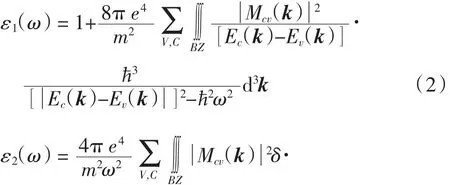
式（2）和式（3）中：e为电子电量；m为自由电子质量；ω为入射光子的频率；BZ为第一布里渊区；c和v分别为导带和价带；k为倒格失；Ec（k）和Ev（k）为导带和价带的本征能量；Mcv（k）为动量跃迁矩阵元.其他光学常数，如折射率n（ω）、反射率R（ω）、吸收系数α（ω）和能量损失函数L（ω）［24］均可由介电函数求出［25］，具体关系式分别为

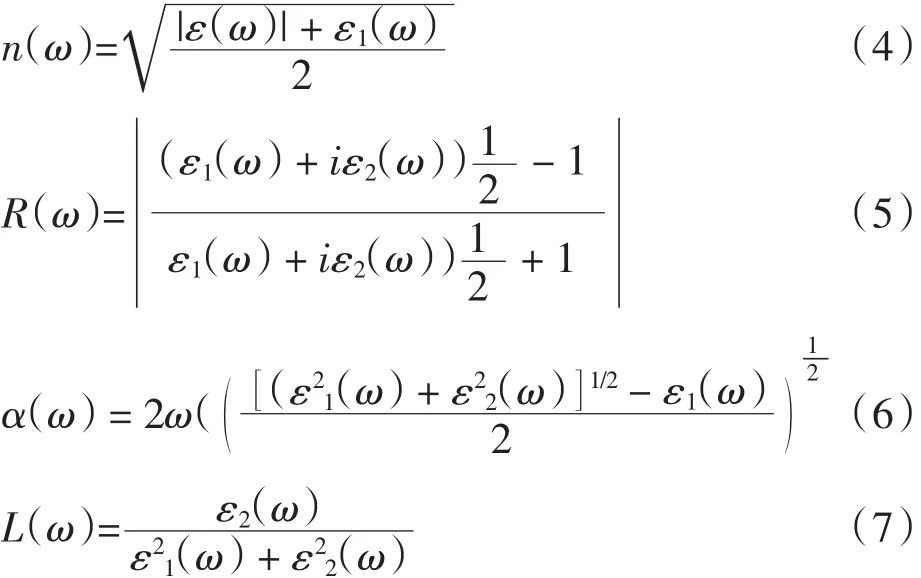
2.2.1 介电函数

图4和图5分别给出了不同应变条件下CaO和SrO复介电函数实部ε1（ω）和虚部ε2（ω）的变化曲线.

图4 不同应变条件下，CaO晶体复介电函数的变化情况Fig.4 Complex dielectric function of CaO under different uniaxial strains

由图4（a）可知，无应变时CaO的静介电常数ε1（0）为2.85，施加单轴拉应变时，静介电常数增加，在η=-15%单轴应变情况下静介电常数降低，分别变为3.227和2.696.在8.33～11.57 eV和26.65～28.58 eV这2个能量范围内，CaO复介电函数的实部出现负值，在这一区域内光无法传播，被称为金属反射区，说明CaO在这些能量范围内表现出金属性质.由图4（b）可以看出，不受应变作用时，ε2（ω）有2个主峰，峰的位置分别在8.21 eV和26.31 eV处.第1个峰值由价带O的p态与导带Ca的d态的电子间跃迁产生，第2个峰值主要源于价带O的s态和导带Ca的d态的电子间跃迁.施加拉应变后2个峰位均稍微向低能量方向移动（产生红移），峰值增大；但在施加压应变条件下，2个峰均分裂成多个峰，且峰值变小.这是由于在单轴压应变条件下，体系的离域性特征增强造成的.从计算结果可以看出，单轴压应变对CaO复介电函数虚部峰值大小的影响比拉应变的影响明显，且第1个峰值附近的曲线受单轴应变影响比较明显.

对比图5可知，在无应变情况下SrO的主峰个数比CaO的主峰个数多，但SrO晶体复介电函数随应变条件下的变化趋势与CaO的基本相同.

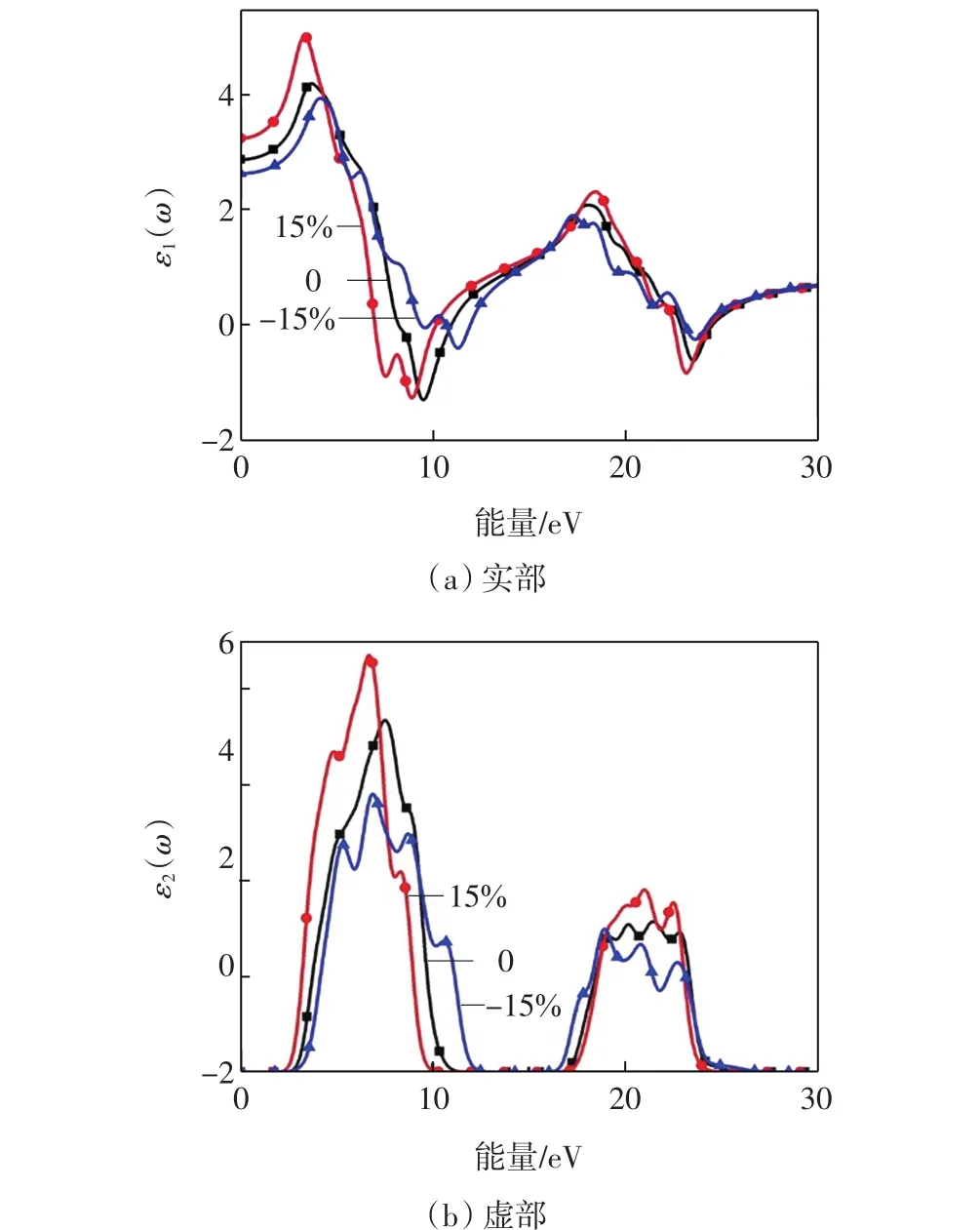
图5 不同应变条件下，SrO晶体复介电函数的变化情况Fig.5 Complex dielectric function of SrO under different uniaxial strains

2.2.2 光学常数

图6和图7为不同应变条件下CaO和SrO晶体折射率、吸收系数、反射率和能量损失函数随光子能量的变化曲线.

由图6（a）和图7（a）可知，在无应变、η=15%单轴拉应变和η=-15%单轴压应变条件下，CaO的静态折射率分别为1.689、1.796和1.641，SrO的静态折射率分别为1.697、1.802和1.623，该结果表明在单轴拉应变情况下静态折射率增大，单轴压应变条件下静态折射率降低，折射率随光子能量变化趋势与复介电函数实部的变化规律基本一致，符合麦克斯韦关系ε1（ω）= n2.在8.33～11.57 eV和26.65～28.58 eV这2个区域内，折射率趋于0，与复介电函数实部金属反射区相对应.

由图6（b）和图7（b）可以看出，不同应变条件下CaO和SrO吸收系数α（ω）的吸收范围均分为2个区域.CaO在未发生应变时吸收范围为2.52～12.46 eV和17.41～29.69 eV，在二者中间的区域无吸收，表明在此能量区域CaO是透明的.无应变时，在CaO第1个吸收范围内，能量为8.94 eV处存在一个峰值0.24.当施加单轴应变后，峰值变化幅度变小，且在拉应变情况下峰值向能量低的方向移动，产生红移，峰值出现在能量为7.86 eV处，这是由于导带中Ca的d态向低能量方向移动，使电子跃迁需要吸收的能量降低.而在施加单轴压应变的条件下，7.73 eV处出现1个弱峰，随着能量的增加在10.16 eV位置上出现1个主峰，峰值为0.19，吸收谱产生蓝移，原因是压应变条件下态密度离域性增强，导带能级展宽，且峰值向能量高的方向移动.在第2个吸收范围内，应变条件对峰位影响很小，单轴拉应变使吸收峰升高，压应变使峰值降低，变化比拉应变情况明显.SrO吸收系数随能量的变化趋势与CaO基本上相同.

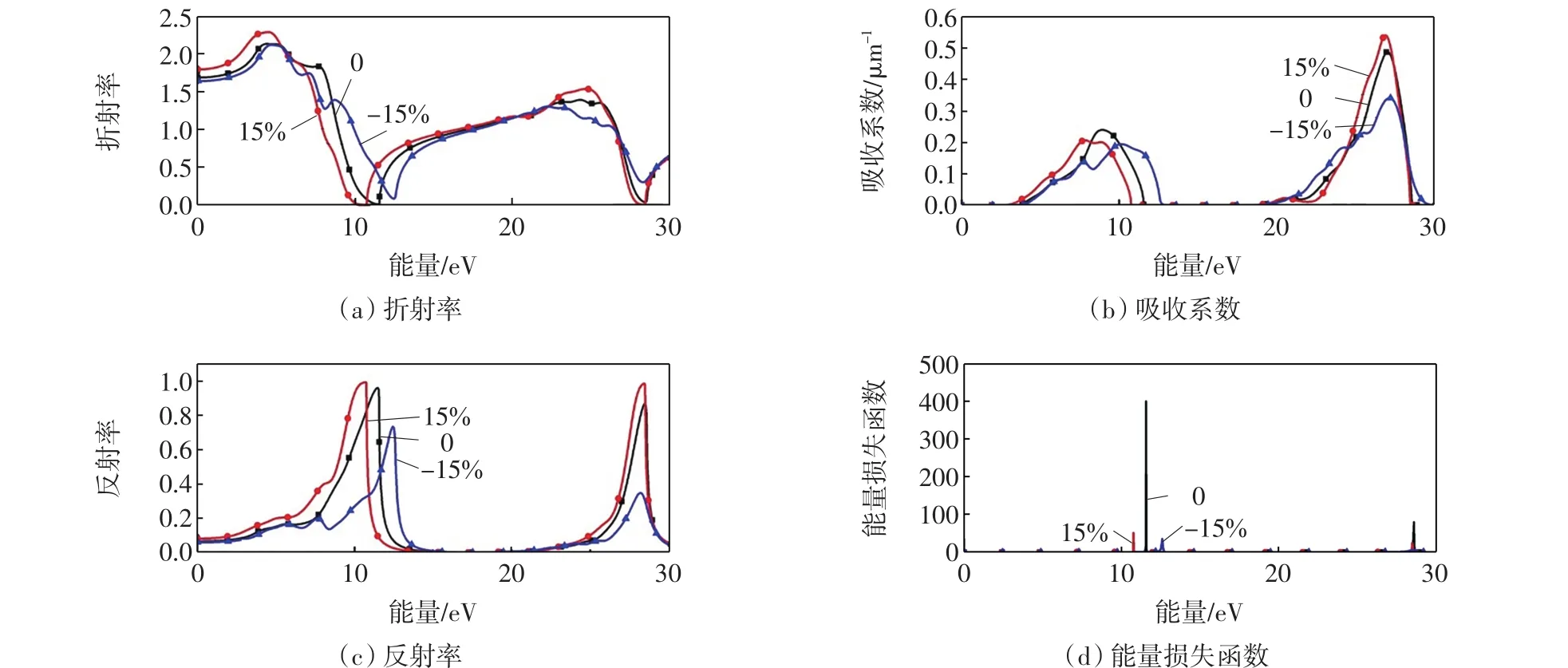
图6 不同应变条件下，CaO光学常数的变化情况Fig.6 Optical constants of CaO under different uniaxial strains

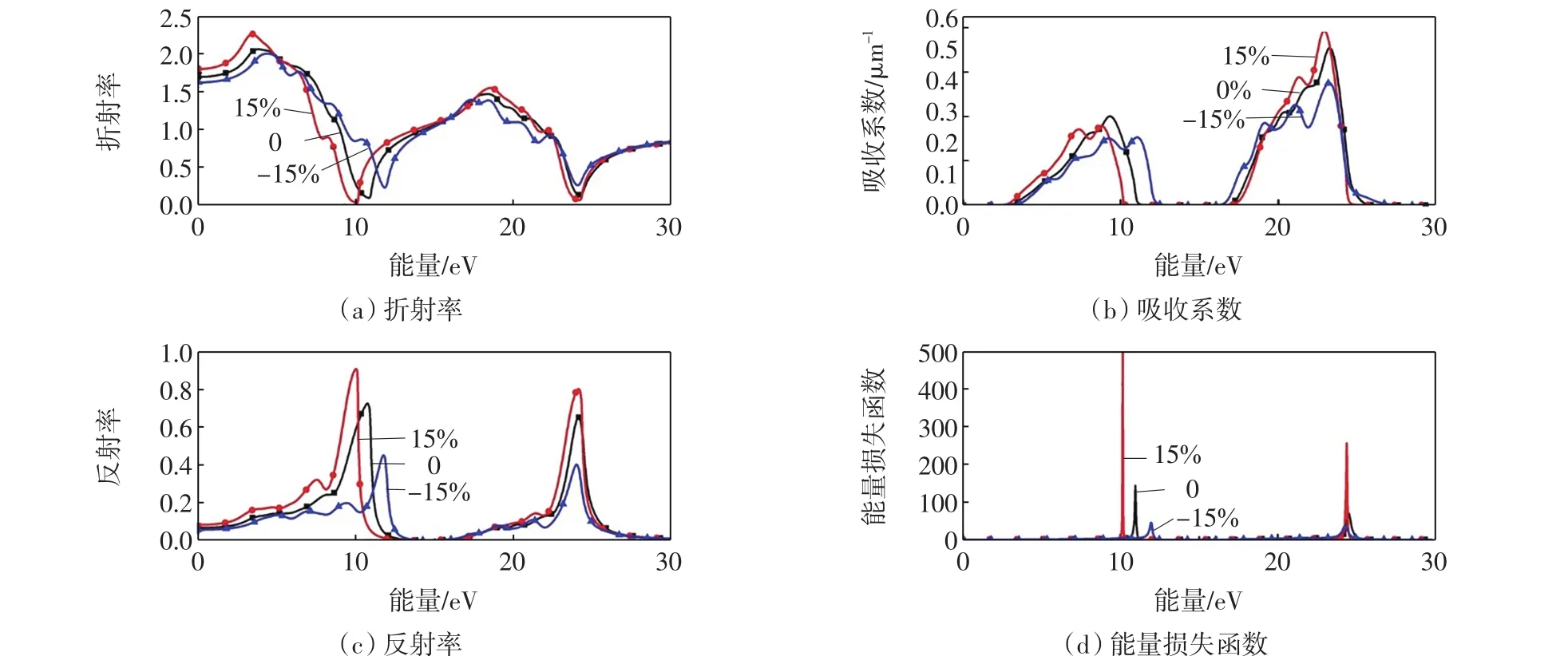
图7 不同应变条件下，SrO光学常数的变化情况Fig.7 Optical constants of SrO under different uniaxial strains

由图6（c）可知，无应变时，CaO的反射率R（0）= 6.6%，光子能量在11.47 eV位置处反射率达到峰值96%，趋近于100%，因为该点位于金属反射区，表现为金属性质，在该点光无法传播，因此反射率接近于100%；同时在28.48 eV位置上另一个反射率峰的峰值为87%.施加单轴拉应变后，第1个反射峰值向能量低的方向移动，且比无应变时峰值增大，同时第2个峰位置变化很小，峰值稍微增大.而在压应变条件下，第1个峰向能量高的方向移动，且峰值增大，第2个峰值显著降低.SrO反射率随能量的变化趋势受单轴应变的影响与CaO的变化趋势基本相同.

L（ω）是重要的光学参数，可以表征电子通过均匀电子介质时能量的损失情形，而能量损失峰则可以描绘等离子的共振频率.由图6（d）和图7（d）可以看出，单轴应变对2种材料的影响存在很大差别.CaO在无应变时的最大能量损失峰达到399.98，施加单轴应变后，损失峰明显减小，说明等离子共振频率减小；单轴拉应变和单轴压应变使损失峰位分别向能量低和能量高的方向移动.而SrO在单轴拉应变下损失峰明显升高，峰值向能量低的方向移动；在单轴压应变条件下，损失峰降低且向能量高的方向移动.

3 结论

采用基于密度泛函理论的第一性原理计算方法，对单轴应变条件下CaO和SrO的电子结构及光学性质进行系统研究.计算结果表明：

（1）单轴应变可以调节CaO和SrO的带隙，使带隙变窄，从而改变材料的导电性，其主要原因是Ca和Sr导带底中的d态电子向低能量方向移动，且SrO价带顶O的p态电子向高能量方向移动.

（2）单轴压应变使电子体系的离域性增强，且单轴压应变对电子结构的影响比拉应变的影响大.

（3）光子能量在0～15 eV能量范围内，2种材料的复介电函数、折射率、吸收系数和反射率的峰位和峰值受单轴应变的影响明显，单轴拉应变使光学谱的峰位向能量低的方向移动，峰值升高；单轴压应变使光学谱的峰位向能量高的方向移动，峰值降低.

（4）CaO和SrO光学性质受单轴应变影响的变化趋势基本相同，但能量损失情况差别较大，单轴应变使CaO的能量损失明显减小，但单轴拉应变使SrO的能量损失增大.

［1］DAI W，SHUI Z H，LI K，et al.First-principle investigations of CaO （100）surface and adsorption of H2O on CaO（100）［J］.Computational and Theoretical Chemistry，2011，967（1）：185-190.

［2］GHEBOULI B，GHEBOULI M A，FATMI M，et al.First-principles calculations of structural，elastic，electronic and optical properties of XO（X=Ca，Sr and Ba）compounds under pressure effect［J］.Materials Science in Semiconductor Processing，2010，13（2）：92-101.

［3］DUAN Y，QIN L，TANG G，et al.First-principles study of ground-and metastable-state properties of XO（X=Be，Mg，Ca，Sr，Ba，Zn and Cd）［J］.Eur Phys J B，2008，66（2）：201-209.

［4］ANDREW J L，DAVID M F，DAVID O S，et al.Structural，energetic and electronic properties of（100）surfaces for alkaline earth metal oxides as calculated with hybrid density functional theory［J］.Surface Science，2015，642：58-65.

［5］SU M X，YANG R，LI M.Biodiesel production from hempseed oil using alkaline earth metal oxides supporting copper oxide as bifunctional catalysts for transesterification and selective hydrogenation［J］.Fuel，2013，103（1）：398-407.

［6］WANG Z Y，LI X H，ZHANG Y，et al.Effect of alkaline-earth metal oxides on Cu/SiO2-Al2O3catalyst for vapor-phase synthesis of 3-methylindole from glycerol and aniline［J］.Chinese Journal of Catalysis，2012，33（7）：1139-1145.

［7］SKORODUMOVA N V，HERMANSSON K，JOHANSSON B.Structural and electronic properties of the（100）surface and bulk of alkaline-earth metal oxides［J］.Physical Review B，2005，72（12）：125414.

［8］BALTACHEA H，KHENATA R，SAHNOUN M，et al.Full potential calculation of structural，electronic and elastic properties of alkaline earth oxides MgO，CaO and SrO［J］.Physica B，2004，344（1/2/3/4）：334-342.

［9］FRANCISCO G C，JUAN B M.Combustion synthesis process for the rapid preparation of high-purity SrO powders［J］.Materials Science-Poland，2014，32（4）：682-687.

［10］JEANLOZ R，AHRENS T，MAO H K，et al.B1-B2 transition in calcium oxide from shock-wave and diamond-cell experiments［J］.Science，1979，206（4420）：829.

［11］DENG Y，JIA O H，CHEN X R，et al.Phase transition and elastic constants of CaO from first-principle calculations［J］.Physica B，2007，392（1/2）：229-232.

［12］KALPANA G，PALANIVEL B，RAJAGOPALAN M.Electronic arid structural properties of alkaline-earth oxides under high pressure［J］.Phys Rev B，1995，52：4-7.

［13］MEHL M J，HEMLEY R J，BOYER L L.Potential-induced breathing model for the elastic moduli and high-pressure behavior of the cubic alkaline-earth oxides［J］.Phys Rev B，1986，33（12）：8685.

［14］TAURIAN O E，SPRINGBORG M，CHRISTENSEN N E.Self-consistent electronic structures of MgO and SrO［J］.Solid State Commun，1985，55（4）：351-355.

［15］VANDERBILT D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism［J］.Phys Rev B，1990，41（11）：7892-7895.

［16］SEGALL M D，LINDAN P J D，PROBERT M J，et al.First-principles simulation：ideas，illustrations and the CASTE Pcode［J］.Condens Matter，2002，14（11）：2717-2744.

［17］MILMAN V，WINKLER B，WHITE J A，t al.Electronic structure，properties，and phase stability of inorganic crystals：a pseudopotential plane-wave study［J］.Int J Quantun Chem，2000，77（5）：895-910.

［18］PERDEW J P，BURKE K，ERNZERHOF M.Generalized gradient approximations made simple［J］.Phys Rev Lett，1996，77（18）：3865-3868.

［19］MONKHORST H J，PACK J D.Special points for Brillouin-zone integrations［J］.Physical Review B，1976，13（12）：5188-5192.

［20］FISCHER T H，ALMLOF J.General methods for geometry and wave function optimization［J］.The Journal of Physical Chemistry，1992，96 （24）：9768-9774.

［21］MEDEIROSA S K，ALBUQUERQUEA E L，MAIA J F F，et al.Structural and optical properties of CaO［J］.Microelectronics Journal，2005，36（11）：1058-1061.

［22］AMBROSCH C，SOFO J O.Linear optical properties of solids within the full potential linearized augmented plane wave method［J］.Comput Phys Commun，2006，1751：1-14.

［23］FOX M.Optical Properties of Solids［M］.New York：Oxford University Press，2001.

［24］RAVINDRAN P，DELIN A，AHUJA R，et al.Optical properties of monoclinic SnI2from relativistic first-principles theory［J］.Phys Rev B，1997，56：6851-6861.

（责任编校 亢原彬）

First-principle study on the electronic structures and optical properties of CaO and SrO under uniaxial strains

XING Meijing，LIANG Kai，YAO Qianqian，LI Shi，SHEN Jie，ZHAO Hui
（College of Physics and Materials Science，Tianjin Normal University，Tianjin 300387，China）

In order to investigate the impact of uniaxial strain on the electronic structure and optical properties of alkaline earth metal oxides CaO and SrO，the energy band structure，density of states and the dielectric function of the crystals were calculated using the first-principle calculation and density-functional theory（DFT）method，and the optical constants were obtained based on Kramers-Kroning relations.The calculated results show that CaO and SrO crystals are both wide and direct band gap insulators in the case of no strain.The band gaps widths of two materials decrease with both uniaxial tensile and compressive strain，in these two cases their conductivities are enhanced，and the influence of compressive strain on the electronic structure of CaO（SrO）is more obvious than tensile strain.The two crystals are both isotropic materials，the uniaxial tensile strain makes the static dielectric constant larger，and the uniaxial compressive strain makes the static dielectric constant smaller.The peaks of positions and values of refractive index of the two material refractive index，absorption coefficient and reflectivity are influenced obviously by uniaxial strain in the energy range from 0 to 15 eV.The uniaxial tensile strain makes each optical spectrum peak moving towards the direction of lower energy and the peak value becoming higher，and the uniaxial compressive strain makes optical spectrum peak position moving towards the direction of higher energy and the values of peaks becoming lower.The static dielectric constant and refractive index of two crystals are both increase with uniaxial tensile strain and decrease with uniaxial compressive strain.The study shows that uniaxial strain can effectively adjust the electronic structure and optical properties of CaO and SrO.

CaO crystal；SrO crystal；first-principle；uniaxial tensile strain；uniaxial compressive strain；electronic structure；optical properties

O482.31

A

1671-1114（2016）03-0021-07

2015-12-02

邢美静（1991—），女，硕士研究生.

赵 辉（1965—），男，教授，主要从事凝聚态理论和计算物理方面的研究.