基于商空间理论的海量生物信息多粒度表示方法

贺丽梅，尹 昕，刘晓倩，赵智伟

（天津师范大学电子与通信工程学院，天津300387）

基于商空间理论的海量生物信息多粒度表示方法

贺丽梅，尹 昕，刘晓倩，赵智伟

（天津师范大学电子与通信工程学院，天津300387）

微操作中，为研究微小目标的生物机理，需要连续获取海量微小目标的生物信息并进行特征分析与建模.针对微操作中海量生物信息多尺度、多层次和结构复杂的特点，利用商空间理论实现海量生物信息的多粒度表示，并将提取的多粒度特征运用于对显微图像进行匹配，以验证本研究算法的有效性.结果表明：算法全面且有效地描述了显微图像目标灰度、纹理和尺度空间方面的特征信息，可以为图像匹配、图像识别和图像检索等图像处理过程提供自适应特征信息，且满足实时性要求.

微操作；显微图像特征提取；商空间理论；粒度计算

随着科技的发展，微操作技术在生物医学、微机械和微导航等方面取得广泛应用.在面向生物医学工程的微操作中，显微视觉系统对操作目标的识别和跟踪具有至关重要的作用，为了准确地跟踪目标，需要首先对目标进行描述和特征分析，即从原始显微图像中提取具有稳定性的图像特征.目前常见的图像特征提取方法包括颜色或灰度的统计特征提取、纹理或边缘的提取、代数特征提取（如主成分分析（principle component analysis，PCA）、线性判据分析（linear discriminate analysis，LDA）、独立成分分析（independent component analysis，ICA））以及变换系数特征提取等［1-2］.此外，基于局部考虑的特征提取算法（SIFT算法）也在图像处理技术中被广泛应用.SIFT算法对旋转、尺度缩放和亮度变化具有不变性，对视角变化、仿射变换和噪声也保持一定的稳定性，但该方法所生成的特征向量维数较高，由此带来了较高的时间复杂度和空间复杂度［3］.近年来，很多研究者参考人类视觉系统提取特征的模式提出基于神经网络的目标特征获取方法［4］，但该方法无法满足微操作中目标跟踪实时性的要求.

随着数据采集、存储和传输技术的飞速发展，显微图像的数据规模越来越大，传统的特征提取方法实时性较差，这就要求探索针对海量生物信息获取和表达的高效方法，而粒度计算不再以数学上的精确解为目标而是寻求最优解，从而降低了求解问题的复杂度，且对计算中数据的不确定性具有很强的适应能力，计算速度快，因此在大规模数据处理上具有的优势.基于上述分析，本研究提出将粒度计算理论引入海量微观生物信息的获取和表达中.作为一种计算模式，粒计算可以模仿人类认知把相似的信息集合在一起.Zadeh于1979年首次提出了模糊信息粒化理论［5-6］，随后许多学者开始了有关粒计算的研究工作.20世纪80年代，波兰学者Pawlak［7］提出粗糙集理论，该方法利用等价关系划分得到近似空间，在近似空间中利用上近似集和下近似集逼近一个边界模糊的集合.2003年，为了探讨粗糙集理论在各种环境下的应用，Castellano以包含度概念研究粒近似空间上的Rough下近似和Rough上近似.刘清等［8］在Rough逻辑的基础上，提出粒-逻辑的概念，构造逻辑的近似推理系统，并应用于医疗诊断.1992年张钹和张铃提出商空间理论，并在文献［9］中系统介绍了该理论.2003年张铃和张钹［10］又将模糊概念与商空间理论结合，提出模糊商空间理论，为粒计算提供了新的数学模型和工具，并成功应用于数据挖掘等领域.随着粒计算的发展，粒计划在人工神经网络、数据挖掘和图像分类检索等方面取得广泛应用［11-14］.当前主要的粒计算模型多基于模糊词计算、粗糙集理论和商空间理论，为了给后续海量生物信息的知识提取提供便利，本研究采用商空间粒计算理论表示海量微观生物信息，并通过实验验证粒度计算在显微图像生物信息表达中的有效性.

1 算法描述

在商空间计算理论中，一个复杂的问题可以使用三元组（X，f，T）进行描述，其中X表示原问题的论域；f为属性函数，即f：X→Y，其中Y可以表示为实数、n维空间Rn或普通的空间，f可以是单值或多值；T为论域结构，表示论域X中不同元素间的相互关系.根据不同的等价关系R，对原问题（X，f，T）进行划分，可以获得不同原问题的商空间（［X］，［f］，［T］）.

1.1 多粒度表达的商空间描述

利用三元组A=（X，f，T）表示海量显微图像中蕴含的生物信息，利用不同的商空间（［Xi］，［fi］，［Ti］）表示对海量显微生物信息进行多粒度表达后的结果，从“细”的粒度世界（X，f，T）转换到“粗”的粒度世界（［Xi］，［fi］，［Ti］）需要采用对应的等价关系R进行划分，这个等价关系就是显微图像中蕴含的需要表达的某方面信息.

1.2 粒度的划分

对问题进行粒度划分是构成不同粒度世界的方法，对于显微图像中的生物信息，从属性层面选取不同的粒度可以更加全面、充分地表达显微图像的信息.由于图像的灰度特征具有一定的稳定性和鲁棒性，且目前很多显微图像均为灰度图像而非彩色图像，本研究选用灰度特征作为第1种粒度对显微图像中的生物信息进行商空间划分；纹理特征可以反映显微图像中目标的组织表面结构排列等微观信息，因此选取纹理特征作为第2种粒度对显微图像的生物信息进行商空间划分；多尺度空间特征的表达可以用简单的形式使图像特征得到不同尺度上的描述，因此选取多尺度空间特征作为第3种粒度对显微图像的生物信息进行商空间划分.

1.3 属性特征提取

1.3.1 灰度特征粒度下属性特征提取

灰度直方图是一种灰度特征提取的经典算法，其构造为

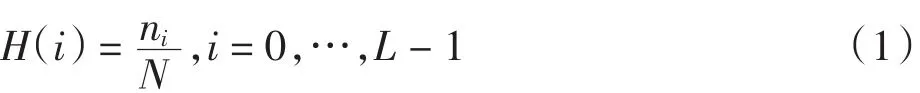
式（1）中：i为灰度级；L为灰度级种类数；ni为图像中灰度级为i的像素个数；N为图像总像素个数.

本研究采用以下统计量反映图像的灰度直方图［15］：

（2）灰度方差反映图像灰度在数值上的离散分布情况.

1.3.2 纹理特征粒度下属性特征提取

本研究采用灰度共生矩阵进行纹理特征的提取.灰度共生矩阵用Pd（i，j）（i，j=0，1，2，…，L-1）表示，其中L为图像的灰度级；i和j分别表示像素的灰度.d 为2个像素间的位置关系，不同的d决定2个像素间的距离和方向；θ为灰度共生矩阵的生成方向，一般取0°、45°、90°和135°共4个方向.选定d后，即生成1个灰度共生矩阵，设灰度值的级数为L，则共生矩阵的元素有L2个.共生矩阵的1个元素代表1种灰度组合出现的次数，如元素Pd（1，1）代表图像上位置关系为d 的2个像素灰度分别为1和1的情况出现的次数.灰度共生矩阵的像素对如图1所示，则灰度共生矩阵

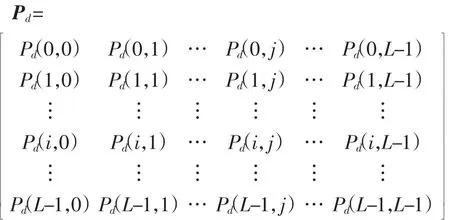
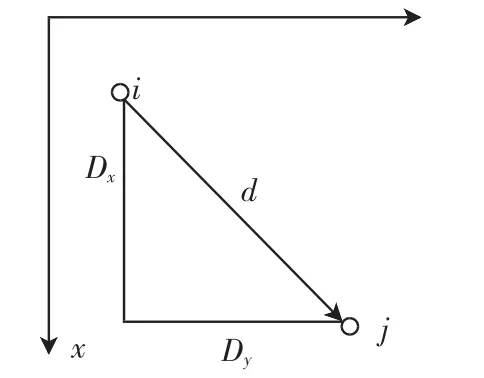
图1 灰度共生矩阵的像素对Fig.1 Pixel pair of gray-level co-occurrence matrix

共生矩阵描述纹理状况时4个常用的特征参数［16］分别为：

1.3.3 尺度空间粒度下属性特征提取

尺度空间理论在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取.图像的尺度空间L（x，y，σ）定义为一个变化尺度的高斯函数G（x，y，σ）与原图像I（x，y）的卷积，即

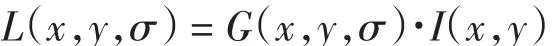
为了使特征描述具有旋转不变性，使用图像梯度的方法求取局部结构的稳定方向.梯度的模值和方向为

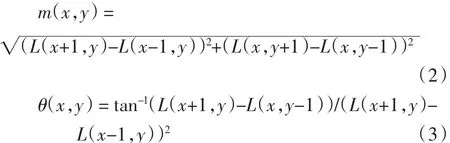
式（2）和式（3）中：L为关键点所在的尺度空间值.梯度计算后，使用直方图统计邻域内像素的梯度和方向，方向直方图的峰值方向代表了该特征点处邻域梯度的主方向，为了增强匹配的鲁棒性，只保留峰值大于主方向峰值80%的方向作为该关键点的辅方向.

综上所述，对于海量微观生物信息的多粒度表示过程，具体算法如图2所示.

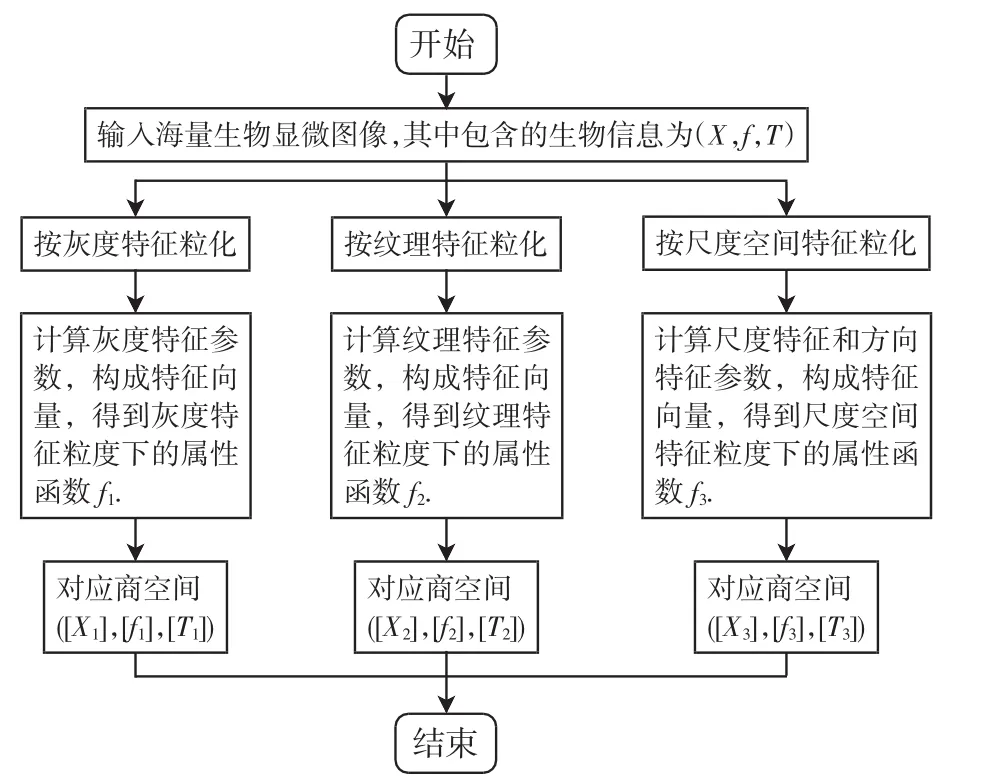
图2 海量微观生物信息多粒度表示的算法流程图Fig.2 Flowchart of multi-granularity modeling for the massive microscopic biological information

2 实验结果与分析

在MATLAB7.0开发环境下进行编程和仿真，选取鸡胚胎细胞显微图像序列中的4帧图片作为实验对象，如图3所示，其中图3（a）、图3（b）、图3（c）和图3（d）分别为显微图像序列中的第1帧、第2帧、第3帧和第4帧.

图3 鸡胚胎细胞显微图像Fig.3 Microscopic images of chicken embryo cells

2.1 显微图像灰度特征提取

在MATLAB7.0中分别读取图3（a）、图3（b）、图3（c）和图3（d），对显微图像灰度直方图统计量进行计算，结果如表1所示.

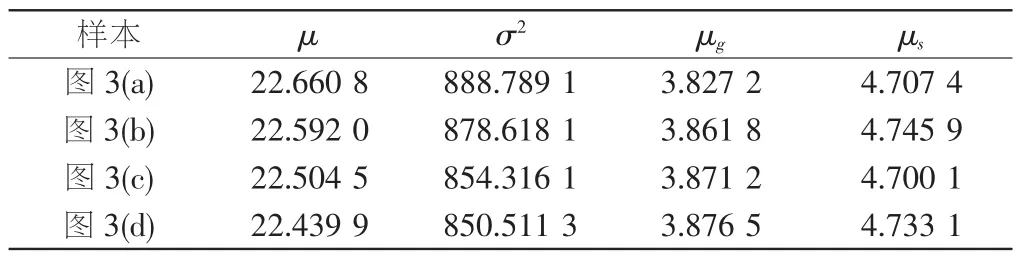
表1 显微图像灰度直方图统计量提取结果Tab.1 Feature parameters of gray-scale histograms

2.2 显微图像纹理特征提取

首先对原始显微图像进行灰度级压缩，将gray量化为16级，然后分别从0°、45°、90°和135°共4个角度分别生成4个共生矩阵，并计算二次距（能量）、对比度（惯性矩）、相关、熵的均值和标准差作为纹理特征，具体结果如表2所示.

2.3 显微图像尺度空间特征提取

将原始显微图像进行不同尺度空间的关键点检测，并统计出这些点对应的尺度参数和方向参数，图3中各图部分关键点的尺度参数L和方向参数O如表3所示.

表2 显微图像纹理特征提取结果Tab.2 Results of texture feature extraction

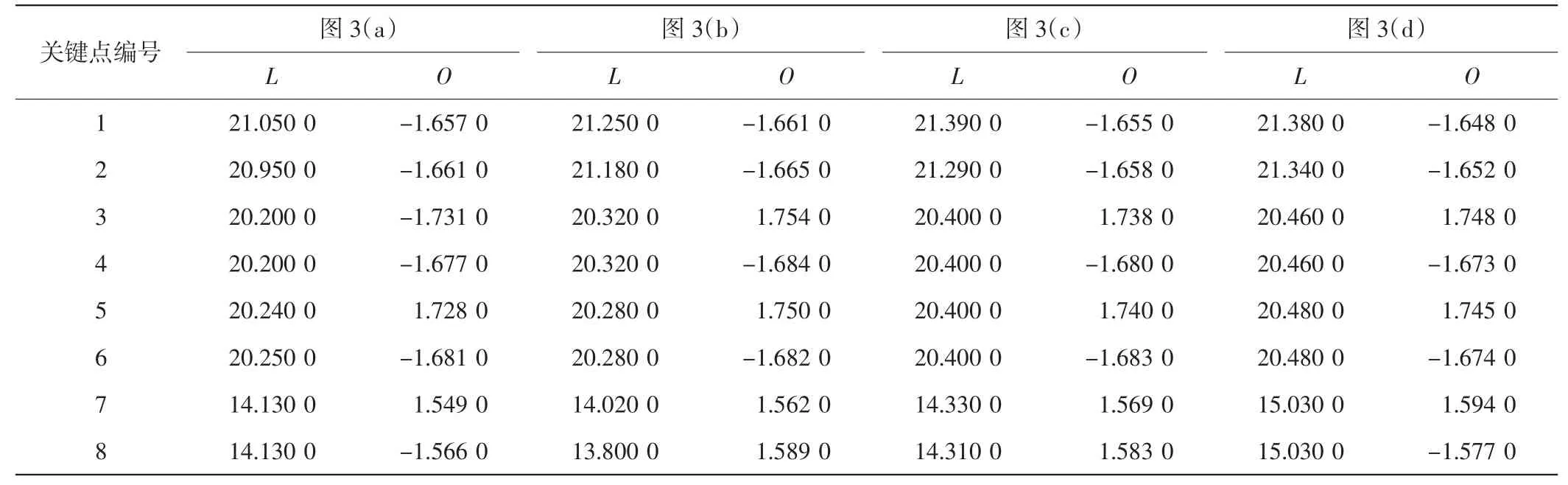
表3 显微图像尺度空间特征提取结果Tab.3 Results of microscopis images by scale space feature extraction

分别对图3进行灰度特征、纹理特征和尺度空间特征提取，所得特征可以全面地表达图像中的信息.为验证本研究算法的有效性，利用这些特征进行图3（a）与图3（b）、图3（c）和图3（d）间的匹配.作为对比，从图3（a）中截取含有显微目标的图片作为模板图（图4），利用灰度模板匹配法以图4为模板图，以图3（b）、图3（c）和图3（d）为实时图进行匹配，从而比较2种匹配方法对显微图像序列的匹配效果，结果如表4所示.

图4 灰度模板匹配的模板图Fig.4 Template of gray template matching

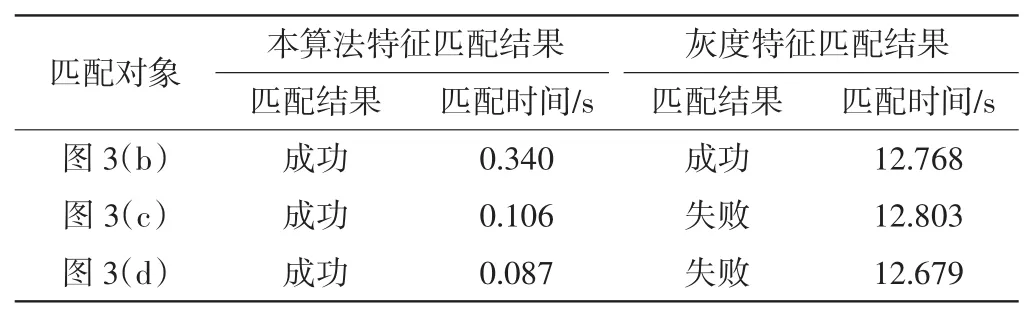
表4 显微图像匹配结果Tab.4 Matching results of microscopic images

由表4可以看出，利用本研究算法所提取的多粒度特征进行显微图像匹配，匹配效果较好，且具有较低的时间复杂度；而灰度特征模板匹配时匹配效果不理想，且灰度特征匹配法的时间复杂度较高.

3 结论

本研究针对显微图像海量、噪点多、多尺度和结构复杂等特点，利用商空间粒计算模型实现了对海量微观生物信息的商空间粒化和多粒度表示，多层次、多侧面地描述了显微图像的特征.①分别将灰度特征、纹理特征和尺度空间特征作为3种粒度，实现显微图像生物信息的多粒度表示；②利用这些特征对显微图像序列进行匹配，验证了多粒度提取显微图像特征的有效性；③利用本研究提取的多粒度特征可以为图像匹配、图像识别、图像检索等图像处理过程提供自适应特征信息，并满足其实时性要求.

［1］MARTINEZ A M，KAK A C.PCA versus LDA［J］.Transactions on Pattern Analysis and Machine Intelligence，2001，23（2）：228-233.

［2］HYVARINEN A，OJA E.Independent component analysis：algorithms and applications［J］.Neural Computation，2000，13（4/5）：411-430.

［3］戴金波.基于视觉信息的图像特征提取算法研究［D］.长春：吉林大学，2013.DAI J B.Algorithms of Image Feature Extraction Based on Visual Information［D］.Changchun：Jilin University，2013（in Chinese）.

［4］WANG Z Y，CU P，LI F T，et al.A data-driven study of image feature extraction and fusion［J］.Information Sciences，2014，281：536-558.

［5］ZADEH L.Fuzzy logic=computing with words［J］.Transactions on Fuzzy Systems，1996，4（1）：103-111.

［6］ZADEH L.Some reflections on soft computing，granular computing and their roles in the conception，design and utilization of information/intelligent systems［J］.Soft Computing，1998，2（1）：23-25.

［7］王国胤，张清华，胡军.粒计算研究综述［J］.智能系统学报，2007，2（6）：8-26.WANG G Y，ZHANG Q H，HU J.An overview of granular computing［J］.CAAI Transactions on Intelligent Systems，2007，2（6）：8-26（in Chinese）.

［8］刘清，刘少辉，郑非.Rough逻辑及其在数据挖掘中的应用［J］.软件学报，2001，12（3）：415-419.LIU Q，LIU S H，ZHENG F.Rough logic and its applications in data mining［J］.Journal of Software，2001，12（3）：415-419（in Chinese）.

［9］张铃，张钹.问题求解理论及应用［M］.北京：清华大学出版社，2007.ZHANG L，ZHANG B.Problem Solving Theory and Its Application［M］.Beijing：Tsinghua University Press，2007（in Chinese）.

［10］张铃，张钹.模糊商空间理论（模糊粒度计算方法）［J］.软件学报，2003，14（4）：770-776.ZHANG L，ZHANG B.Theory of fuzzy quotient space（methods of fuzzy granular computing）［J］.Journal of Software，2003，14（4）：770-776（in Chinese）.

［11］SCOTT D，ANDREW T，CURTIS B，et al.A granular neural network：performance analysis and application to regranulation［J］.International Journal of Approximate Reasoning，2013，54（8）：1149-1167.

［12］PIOTR H.Granular computing for relational data classification［J］.Joural of Intelligent Information Systems，2013，41（2）：187-210.

［13］PIOTR H.Association discovery from relational data via granular computing［J］.Information Sciences，2013，234：136-149.

［14］郭庆文，王国胤，张清华.多粒度的图像检索方法研究［J］.计算机科学，2013，40（1）：298-310.GUO Q W，WANG G Y，ZHANG Q H.Research on multi-granularity image retrieval method［J］.Computer Science，2013，40（1）：298-310 （in Chinese）.

［15］刘益新，郭依正.灰度直方图特征提取的Matlab实现［J］.电脑知识与技术，2009，5（32）：9032-9034.LIU Y X，GUO Y Z.Gray-scale histograms feature extraction using Matlab［J］.Computer Knowledge and Technology，2009，5（32）：9032-9034（in Chinese）.

［16］ULABY F T，KOUYATE F，BRISCO B，et al.Textural information in SAR images［J］.Transactions on Geoscience and Remote Sensing，1986，24（2）：235-245.

（责任编校 亢原彬）

Multi-granularity modeling for the massive biological information in micro manipulation based on the quotient space theory

HE Limei，YIN Xin，LIU Xiaoqian，ZHAO Zhiwei
（College of Electronic and Communication Engineering，Tianjin Normal University，Tianjin 300387，China）

In micro manipulation，massive tiny biological information need continuously obtaining and its characteristic analysis and modeling need taking to study the mechanism of micro biological objects.For the features like multi-scale，multi-level and complex structure of massive biological information，an algorithm of multi-granularity modeling for massive biological information based on the quotient space theory was realized，and the extracted multi-granularity features were used to microscopic image matching to verify the effectiveness of the algorithm.The results show that multi-granularity features like gray features，texture features and scale space features are described effectively and comprehensively using this algorithm，and the algorithm provides adaptive features and satisfy the request of real time operation for image processing such as image matching，image recognition and image retrieval.

micro manipulation；feature extraction of microscopic image；quotient space theory；granular computing

TP18

A

1671-1114（2016）03-0028-05

2016-01-10

天津市自然科学基金资助项目（13JCYBJC15800）；天津师范大学大学生创新创业训练计划资助项目（201553）.

贺丽梅（1994—），女，本科生.

尹 昕（1973—），女，副教授，主要从事模式识别和智能机器人控制方面的研究.