一类具有Size结构的非线性种群系统的最优控制

李彩彩，赵 春

（天津师范大学数学科学学院，天津300387）

一类具有Size结构的非线性种群系统的最优控制

李彩彩，赵 春

（天津师范大学数学科学学院，天津300387）

研究一类具有Size结构的非线性种群系统的最优控制问题.利用Ekeland变分原理和共轭系统证明了最优控制的存在性，并借助法锥概念得到了最优控制的必要性条件.

Size结构；最优控制；Ekeland变分原理；共轭系统

个体尺度对个体生命参数和种群发展的重要性已经得到了生物学家的广泛认可［1］，并且得到了相关数学家的普遍重视［2］.对基于个体尺度的种群模型的相关研究已取得了较为丰富的结果.文献［3］建立了具Size结构的单种群系统模型，首先用特征线给出了系统的形式解，然后探讨了种群系统的最优控制问题.文献［4-7］分别考虑具有尺度结构的线性、非线性种群动力系统的最优收获问题.文献［8］研究了一类具有尺度结构和加权总规模的种群模型.文献［9-10］对依赖个体尺度结构的种群资源开发模型进行了理论分析.文献［11］研究了一类具有个体尺度的种群模型的最优繁殖率问题.受以上文献思想启发，本研究考虑如下非线性种群系统的最优控制问题

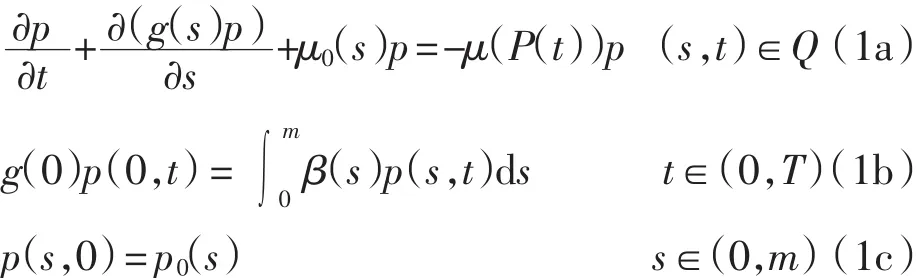
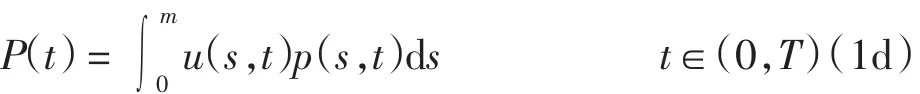
其中：Q=（0，m）×（0，T），固定常数m、T分别为个体所不能超越的最大尺度和控制周期；状态变量p（s，t）为t时刻个体尺度为s的种群个体分布密度；μ0（s）和β（s）分别为个体的自然死亡率和出生率；g（s）为种群个体尺度的增长率；u（s，t）为控制变量.

选取目标函数

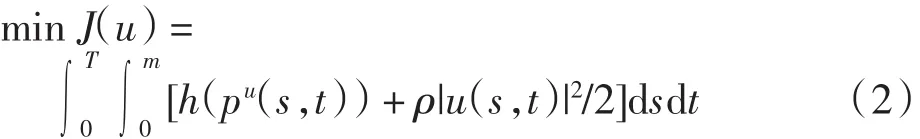
其中ρ为正常数.

允许控制集为

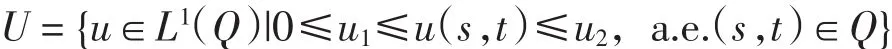
其中u1、u2均为已知常数.

为了讨论系统（1）和（2）的最优控制问题，本研究假设下列条件成立：

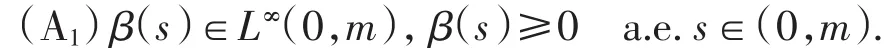
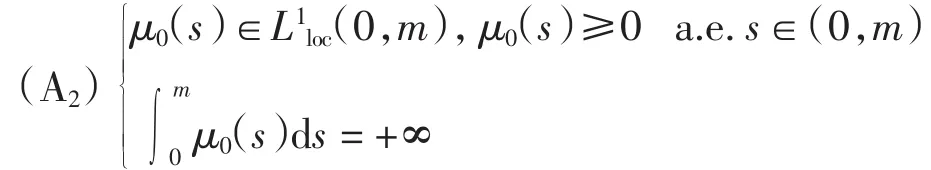
（A3）μ（x）∈C2（R+）.对任意的x∈R+，μ（x）≥0，且|μ′（x）|≤A，|μ″（x）|≤B，其中A、B均为正常数.

（A4）p0（s）∈L∞（0，m）.p0（s）≥0 a.e.s∈（0，m）.

（A5）g（s）∈C1（0，m）.对任意的s∈（0，m），0＜g（s）＜L.

（A6）h（x）∈C2（R+）.对任意的x∈R+，h（x）≥0，且|h′（x）|≤G，|h″（x）|≤H，其中G、H均为正常数.

（A7）μ0、β、g、p0在其定义域外均为0.

定义 称函数p（s，t）为系统（1）的解，若p（s，t）∈L∞（0，T；L1（0，m））在每一条特征线处都绝对连续，且满足下列条件

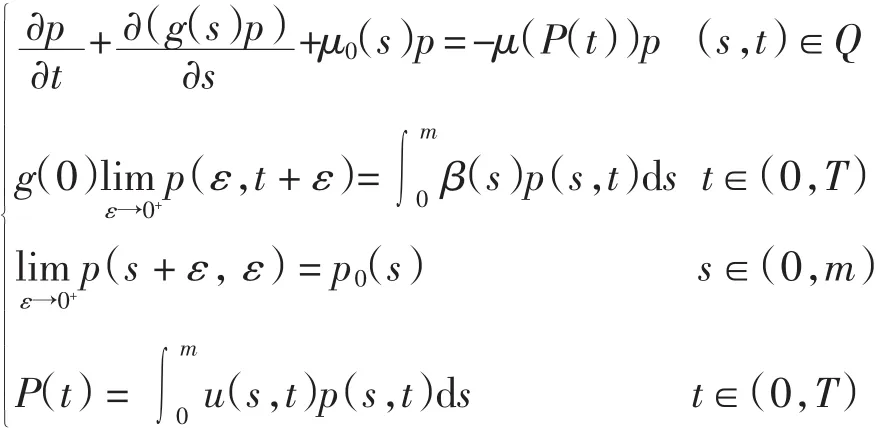
1 预备引理

由文献［8］中的标准证明可得引理1.

引理1 在假设条件下，对于任意给定的u（s，t）∈U，方程（1）存在唯一解p（s，t）∈L∞（0，T；L1（0，m）），且0≤p（s，t）≤M（M为正常数），p（s，t）具有如下表达式

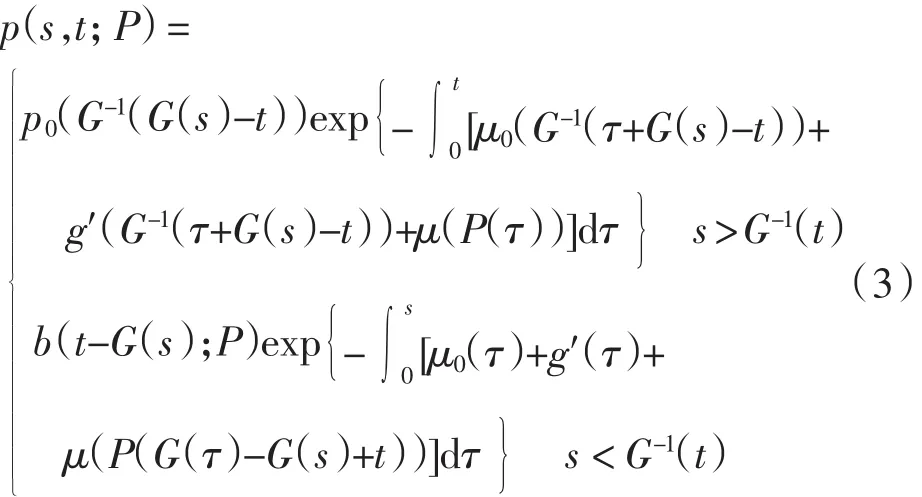
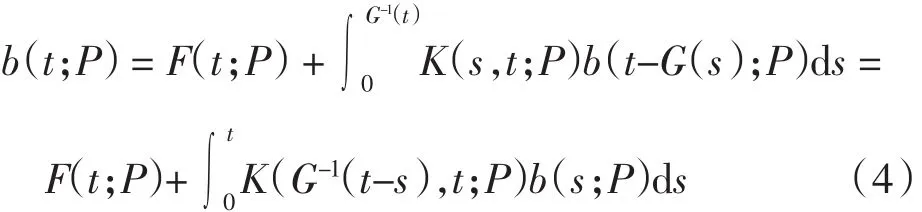
这里

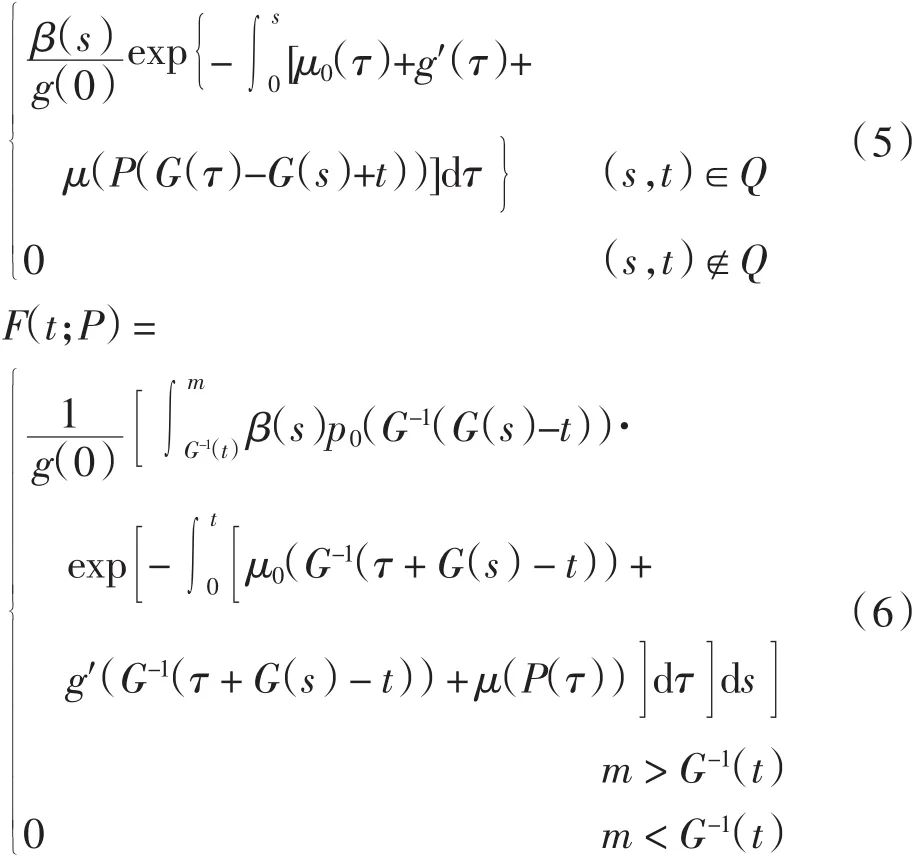
引理2 在假设条件下，存在正常数M1、M2，使得

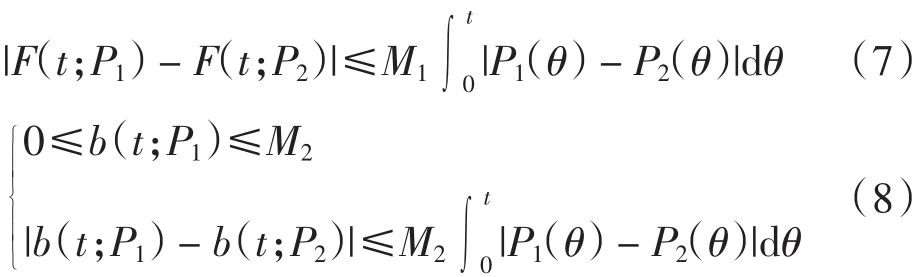
证明 由假设条件和式（5）～式（6）可得

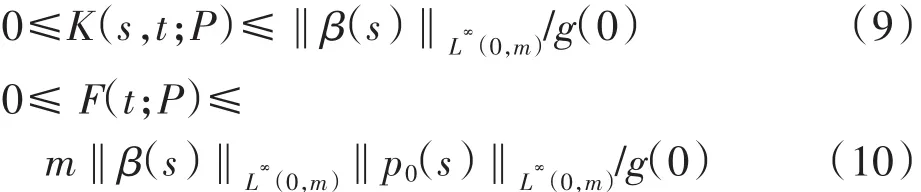
当m＞G-1（t）时，由式（6）可得

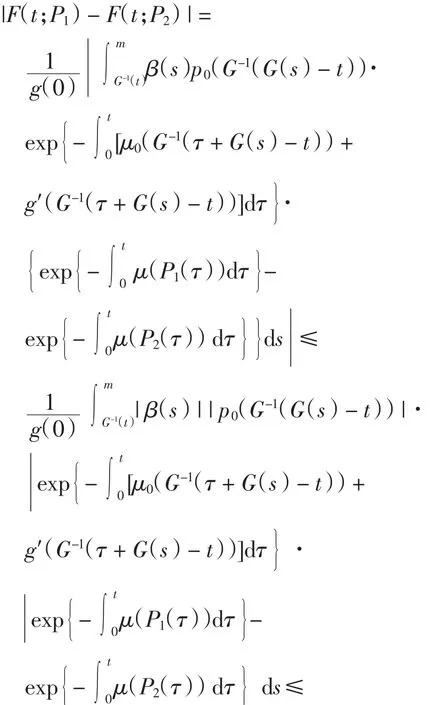
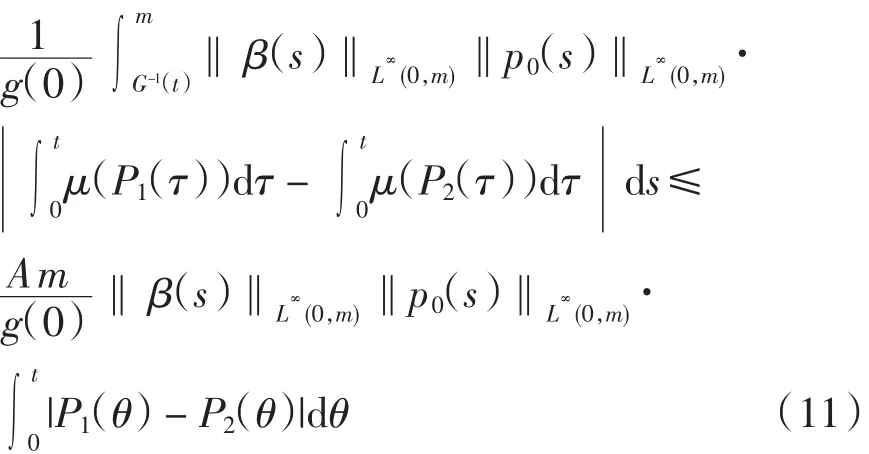
当m＜G-1（t）时，利用式（6）可得

故有

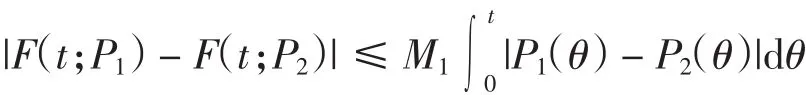
由式（4）～式（6）和式（9）～式（10）可得

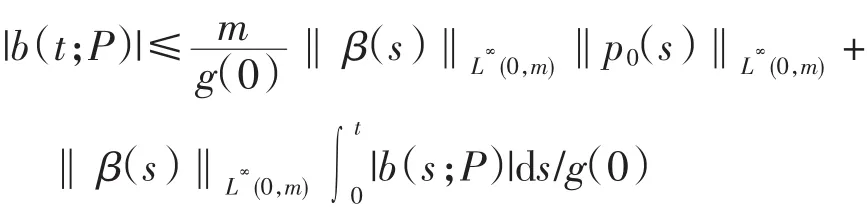
应用Bellman引理可得

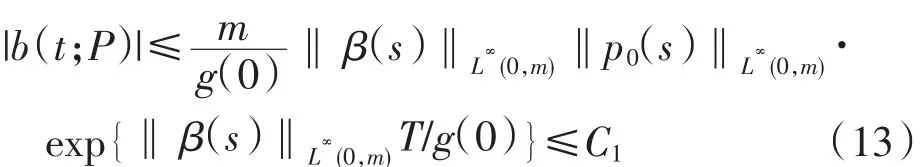
其中

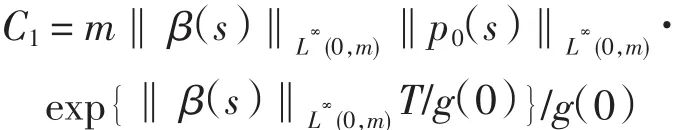
由式（4）～式（7）及式（13）可得

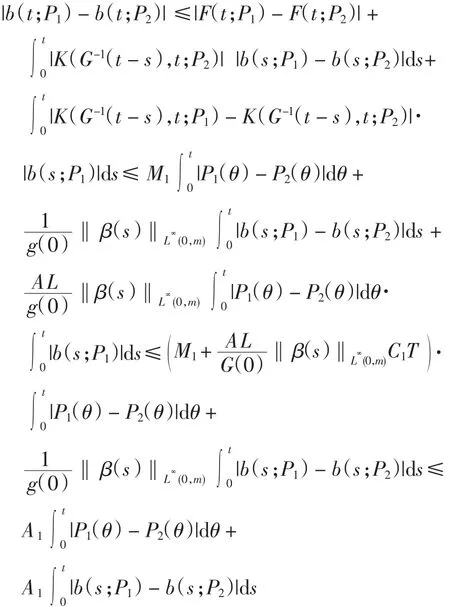
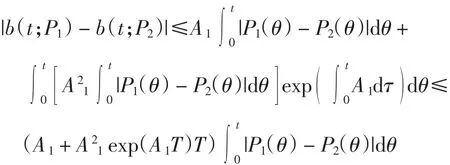
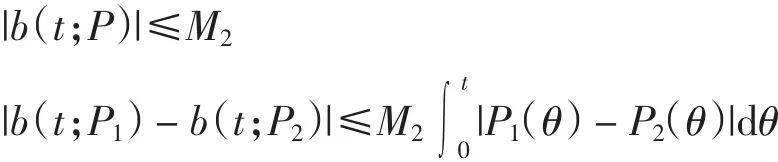
引理3 存在正常数C1、C2，使得对任意的u、v∈U，有

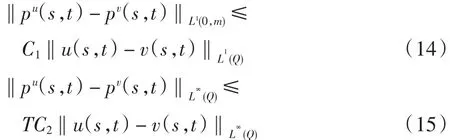
证明 当m>G-1（t）时，由式（3）～式（8）可得

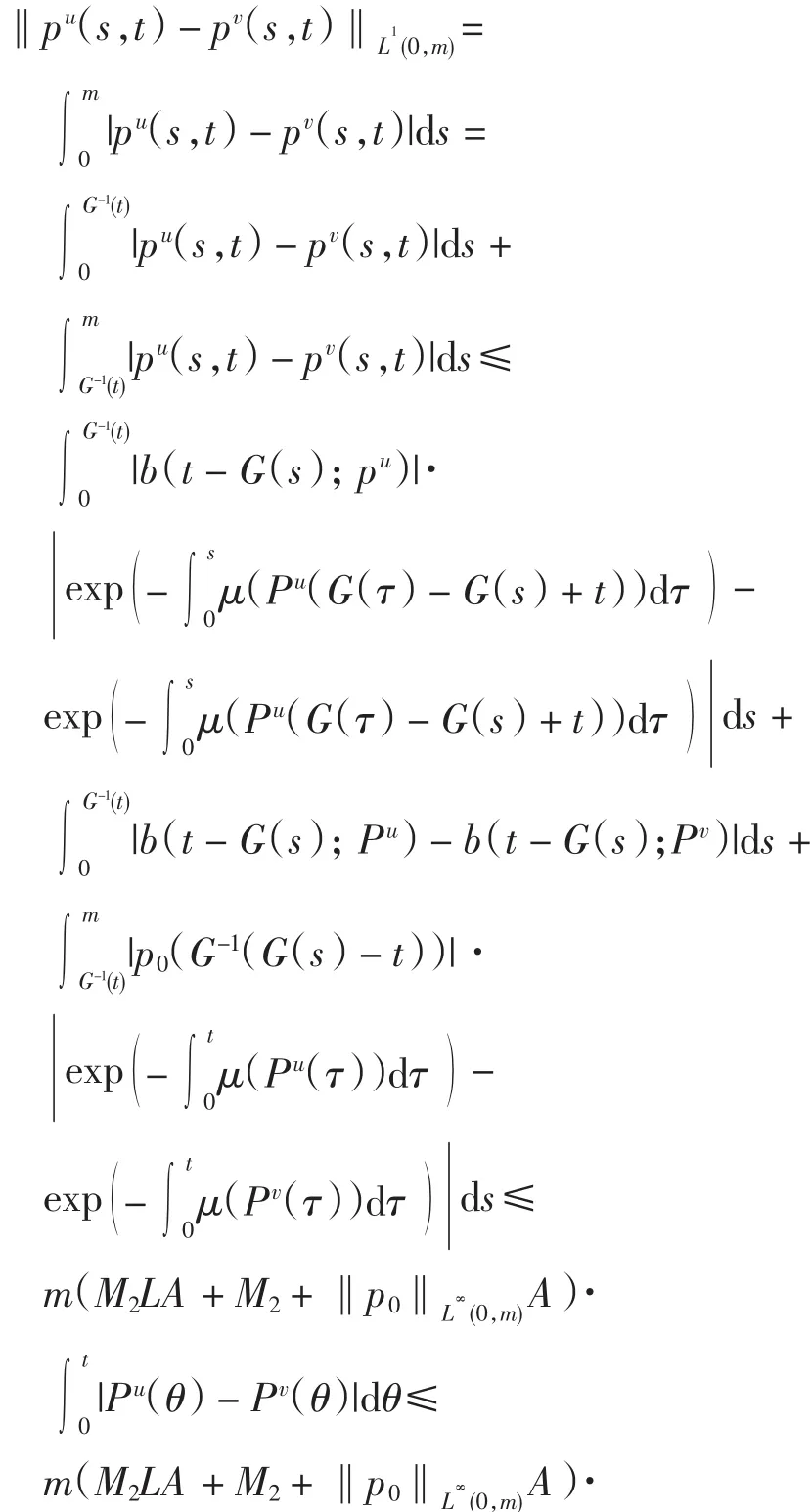
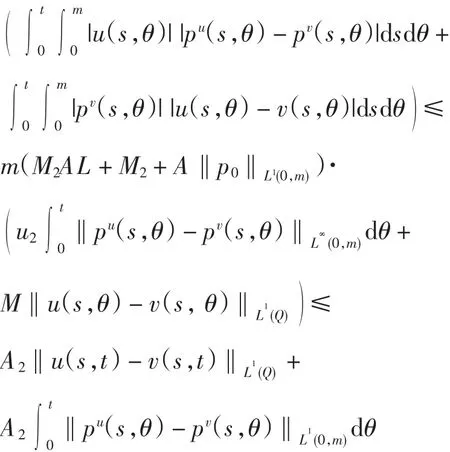
其中

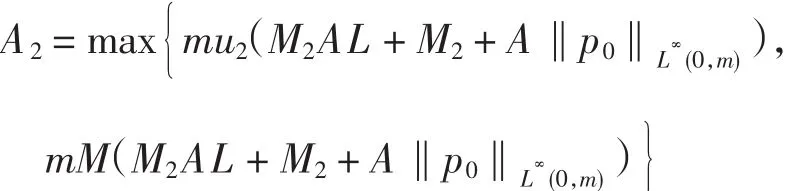
利用Bellman引理可得

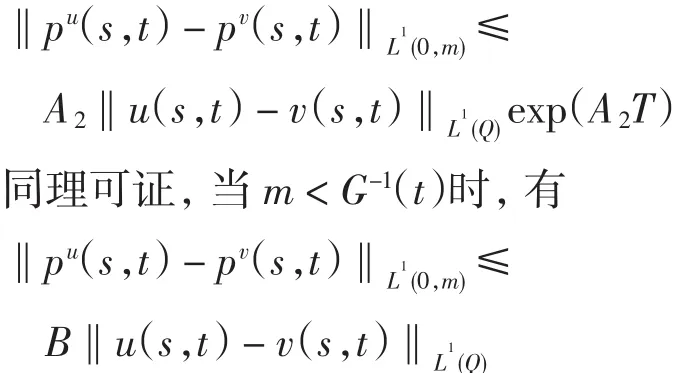
故有

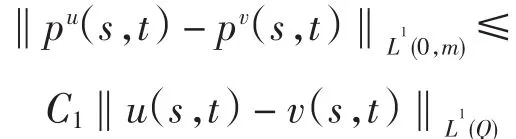
其中C1=max｛B，A2exp（A2T）｝.

当s＞G-1（t）时，由式（3）可得

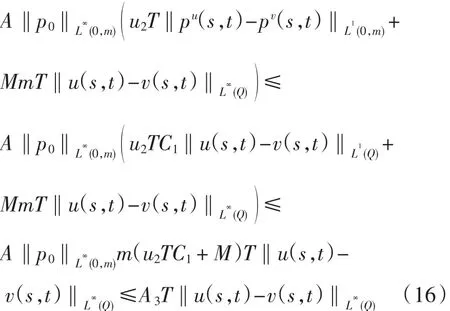
同理可证，当s＜G-1（t）时，有

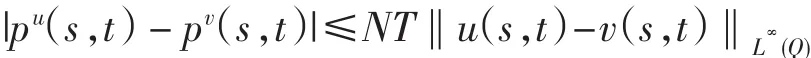
故有

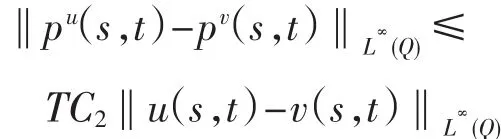
其中C2=max｛N，A3｝.

2 最优控制的存在性

考虑控制问题（2）.定义映射φ：L1（Q）→（-∞，+∞），

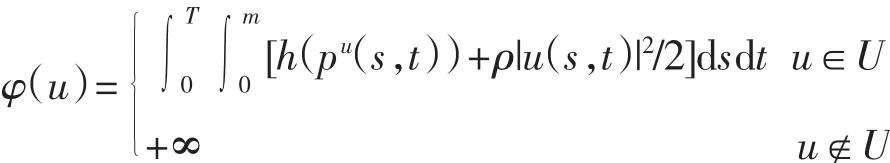
引理4 函数φ是下半连续的.

证明 不失一般性，设｛un｝∈U，｛un｝在L1（Q）中收敛到u，又｛pun｝在L∞（Q）中有界.由引理3可知，在L∞（0，T；L1（0，m））中，有pun（s，t）→pu（s，t）.因此存在子列｛（un，pun）｝，使得

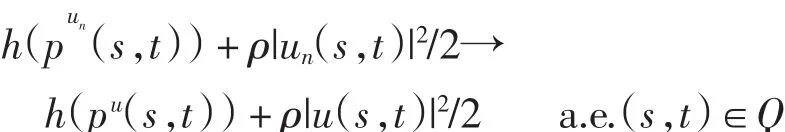
由Fatou引理得

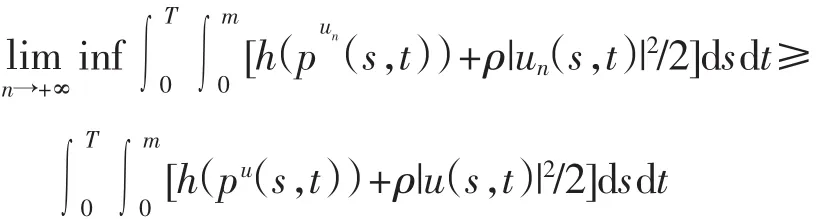
引理5 设｛（u*，pu*）｝是控制问题（1）和（2）的最优解.若对任意的v∈L∞（Q），当ε＞0充分小时，有u*+εv∈U，则在L∞（0，T；L1（0，m））中，当ε→0+时，有

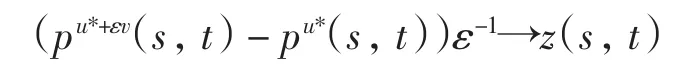
其中z（s，t）满足下列方程

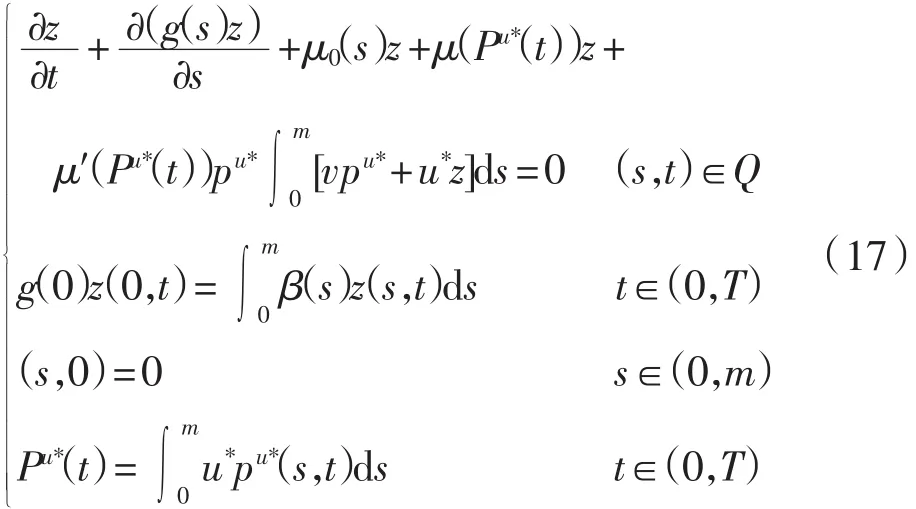
证明 定义

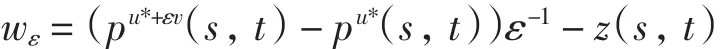
显然wε满足

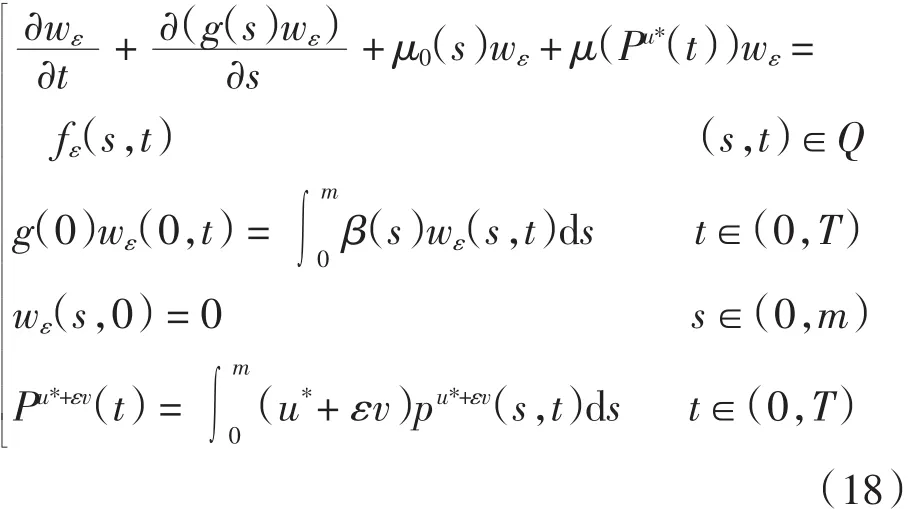
其中

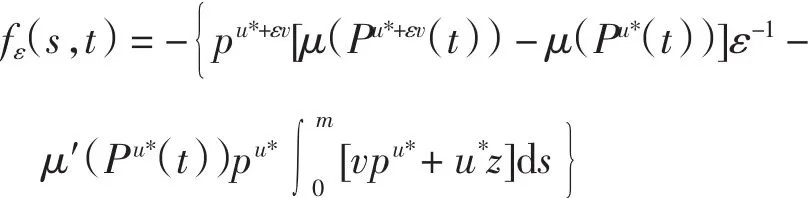
由引理1可知，系统（18）存在如下形式解

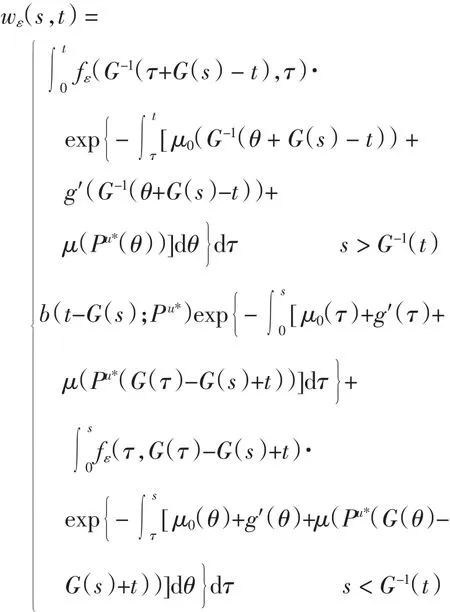
利用与引理3类似的证明方法可得，在L∞（0，T；L1（0，m））中，当ε→0+时，wε（s，t）→0.因此，在L∞（0，T；L1（0，m））中，当ε→0+时，有

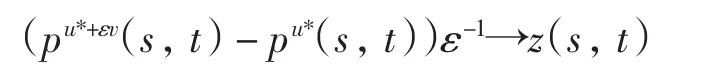
利用与引理3类似的方法可证得引理6.

引理6 设q为下列共轭系统的解

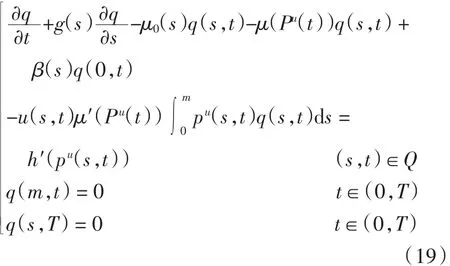
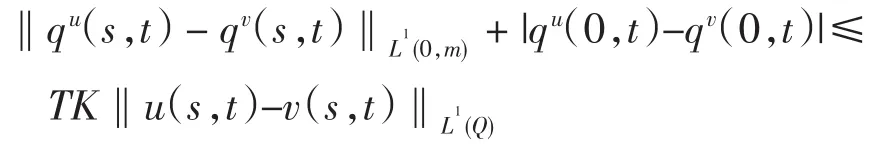
定理1 若T充分小，则存在唯一的最优控制u*∈U.

证明 由引理4知φ是下半连续的，由Ekeland变分原理可得：∀ε＞0，∃uε∈U，使得

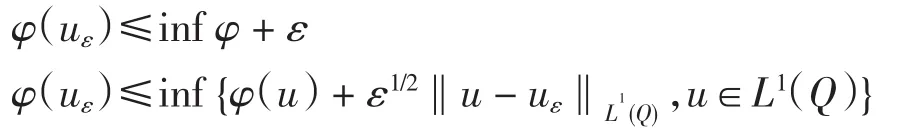
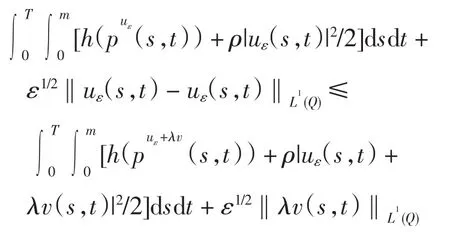
于是有

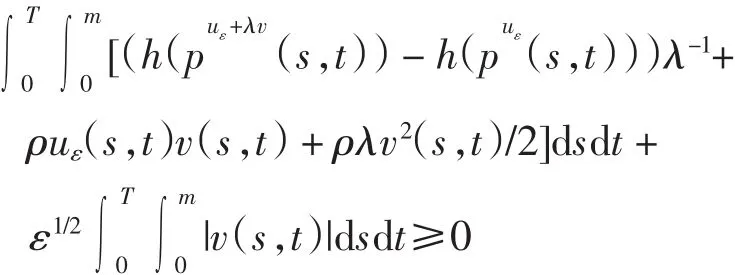
令λ→0+，取极限，并利用引理5可得

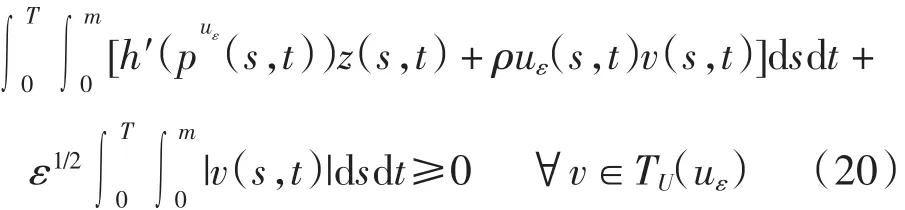
将式（17）的第1个方程两边乘以q（s，t），加上共轭系统（19）的第1个方程两边乘以z（s，t），并在Q上积分，得到

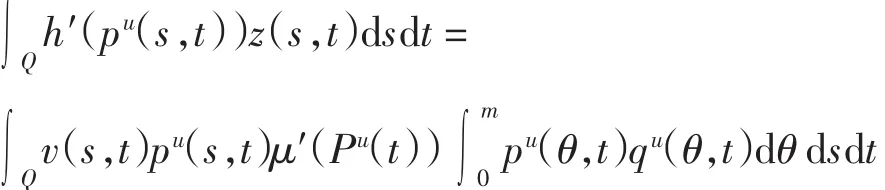
由式（20）可得

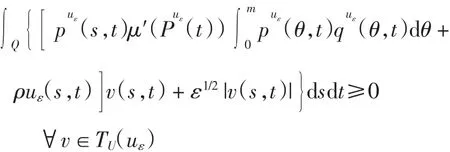
由文献［12］可知，存在ξ∈L∞（Q）且‖ξ‖L∞（Q）≤1，使得

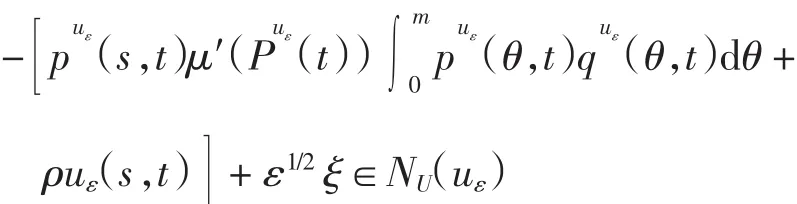
由文献［12］可得

其中映射H：L1（Q）→L1（Q），

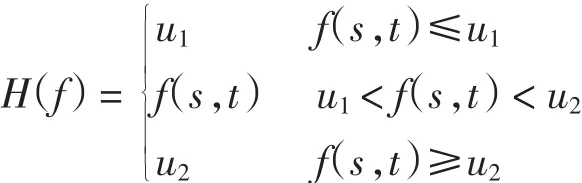
先证最优控制的唯一性.定义算子

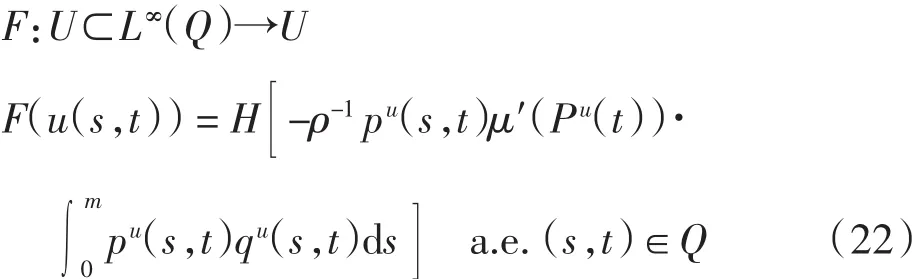
由引理1可知共轭系统的解满足‖q（s，t）‖L∞（Q）≤TL1，这里L1为常数.

由引理3和引理6及假设条件可知

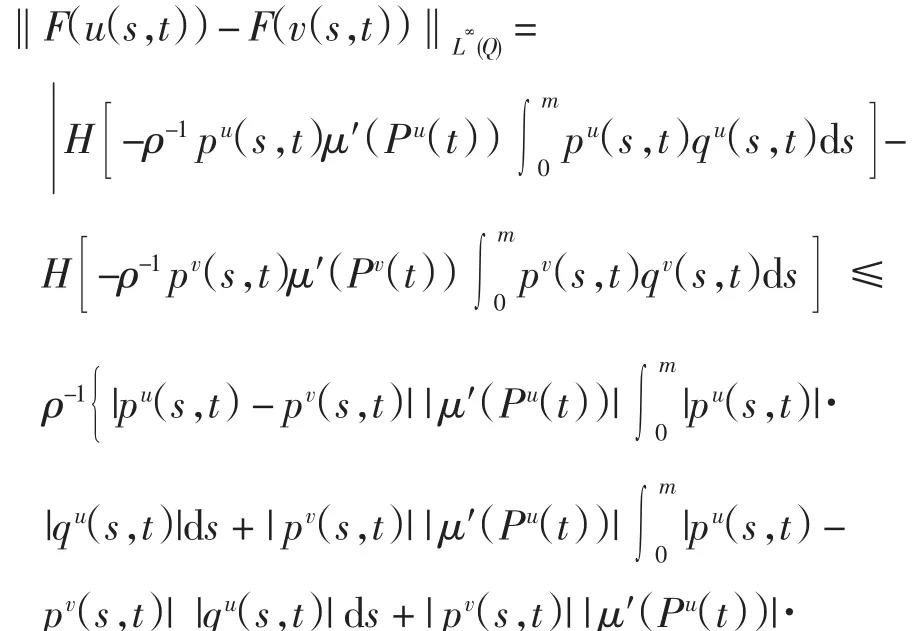
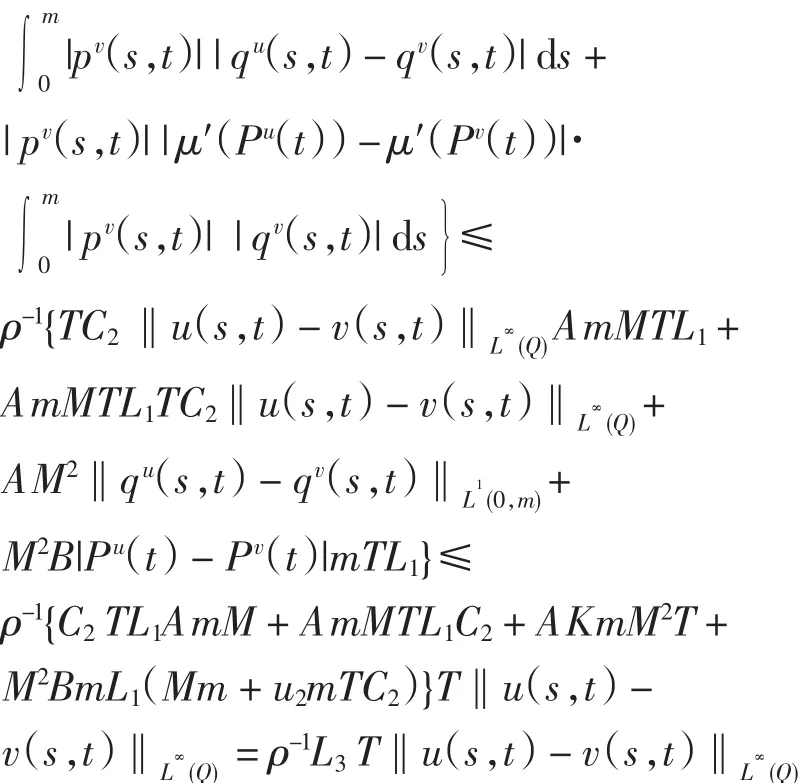
其中L3=TC2L1AmM+AmMTL1C2+AKmM2T+M2BmL1· （Mm+u2mTC2）.当T充分小时，则可使ρ-1L3T＜1.故F是压缩映射，有唯一不动点u*.

下证u*是最优的.由式（21）和式（22）可知

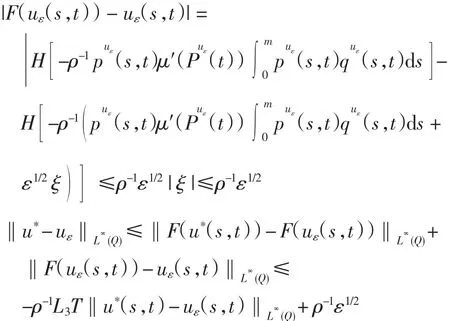
故有

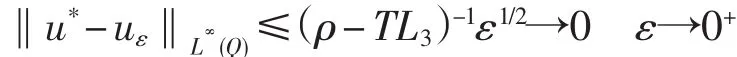
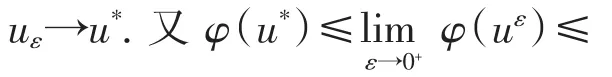
故有

因此u*为最优控制.

3 最优控制的必要条件

定理2 设（u*，pu*）为控制问题（1）和（2）的最优解，qu*为对应于u=u*的共轭系统（19）的解，则有

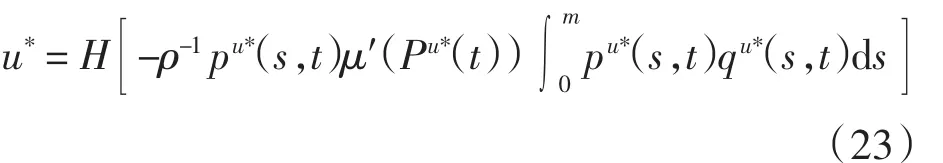
证明 对任意v∈TU（u*）（U在u*处的切锥），当λ≥0充分小时，u*+λv∈U，由于u*为最优解，故有

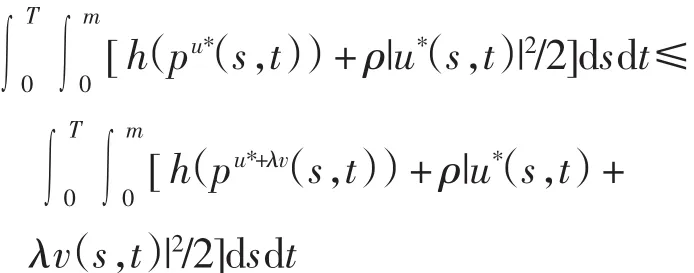
即

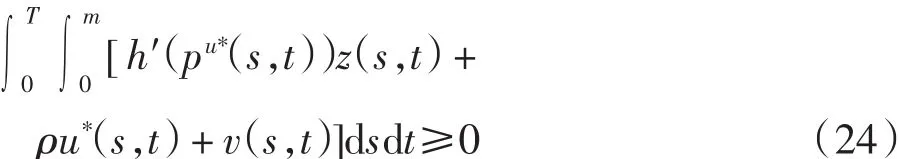
其中z（s，t）是方程（17）的解.将式（17）的第1个方程两边乘以q（s，t），加上共轭系统（19）的第1个方程两边乘以z（s，t），并在Q上积分，得到

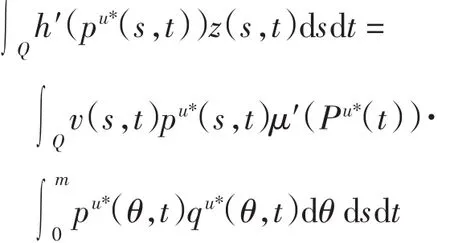
将上式代入式（24），可得

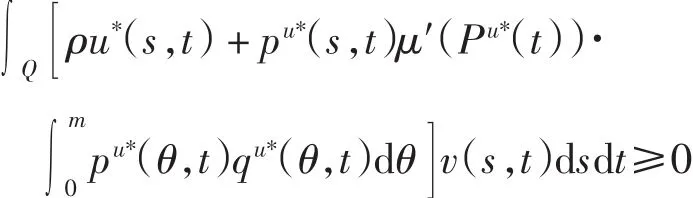
所以

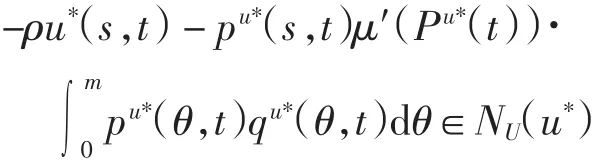
根据法锥的性质即知定理成立.

［1］EBENMAN B，PERSSON L.Size-Structured Populations：Ecology and Evolution［M］.Berlin：Springer-Verlag，1988.

［2］METZ J A J，DIEKMANN O.The Dynamics of Physiologically Structured Populations［M］.Berlin：Springer-Verlag，1986.

［3］WEBB G F.Population models structured by age，Size and spatial position［J］.Lecture Note in Mathematics，2008，36（1）：1-50.

［4］ KATO N.Maximum principle for optimal harvesting in linear Size-structured population［J］.Mathematical Population Studies，2008，15：123-136.

［5］KATO N.Optimal harvesting for nonlinear Size-structured population dynamics［J］.J Math Anal Appl，2008，324：1388-1398.

［6］陈波涛，何泽荣，刘炎.带有Size结构和收获的种群控制系统分析［J］.四川大学学报：自然科学版，2010，47（6）：1238-1244.CHEN B T，HE Z R，LIU Y.Analysis of a Size-structured population control system with harvest［J］.Journal of Sichuan University：Natural Science Edition，2010，47（6）：1238-1244（in Chinese）.

［7］刘炎.具有Size结构的种群动力系统的行为分析和最优控制［D］.杭州：杭州电子科技大学，2009.LIU Y.Behavior Analysis and Optimal Control of Biological Population Dynamical Systems with Size-structure［D］.Hangzhou：Hangzhou Electronic Science and Technology University，2009（in Chinese）.

［8］杨立志，何泽荣，邹世平.具有尺度结构和加权总规模的种群模型分析［J］.应用泛函分析学报，2014，16（3）：212-219.YANG L Z，HE Z R，ZOU S P.Analysis of a population model with Size-structure and weighted size［J］.Acta Analysis Functionalis Applicata，2014，16（3）：212-219（in Chinese）.

［9］何泽荣，刘荣，刘丽丽.依赖个体尺度结构的种群资源开发模型理论分析［J］.系统科学与数学，2012，32（9）：1109-1120.HE Z R，LIU R，LIU L L.Theoretical analysis for a nonlinear Size-structured population resources model［J］.Journal of System Science and Mathematical Sciences，2012，32（9）：1109-1120（in Chinese）.

［10］LIU Y，HE Z R.Stability results for a Size-structured population model with resources-dependence and inflow［J］.J Math Anal Appl，2009，360（2）：665-674.

［11］HE Z R，LIU Y.An optimal birth control problem for a dynamical population model with Size-structure［J］.Nonlinear Analysis：Real World Applications，2012，13（2）：1369-1378.

［12］ANITAS.Analysis and Control of Age-Dependent Population Dynamics［M］.Dordrecht：Kluwer Academic Publishers，2000.

（责任编校 马新光）

Optimal control for a kind of nonlinear Size-structured population systems

LI Caicai，ZHAO Chun
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

The optimal control for a kind of nonlinear Size-structured population systems is studied.The existence of the optimal control is proved by using Ekeland＇s variational principle and adjoint system，and by means of the concept of the normal cone，the necessary conditions of optimality is obtained.

Size-structured；optimal control；Ekeland＇s variational principle；adjoint system

O175.1

A

1671-1114（2016）03-0001-07

2015-11-17

国家自然科学基金资助项目（60972089）.

李彩彩（1988—），女，硕士研究生.

赵 春（1963—），男，教授，主要从事控制论及其应用方面的研究.