一种无汇交轴线对称三转动并联机构的运动分析

陈子明　黄　坤　张　扬　丁华锋　黄　真

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，0660043.中国地质大学,武汉,430074



一种无汇交轴线对称三转动并联机构的运动分析

陈子明1,2黄坤1,2张扬1,2丁华锋3黄真1,2

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，0660043.中国地质大学,武汉,430074

传统的三自由度转动并联机构(又称球面并联机构)一般都有一个转动中心，且这个中心点往往是分支间多个运动副轴线的汇交点，这种严格的几何条件给机构的加工制造带来很大的难度，制约了这类机构的应用。针对此，提出了一种无汇交轴线的对称三转动并联机构，其三个分支对称布置，分支内及分支间均无汇交轴线。对机构进行了位置反解，得到了机构四种对称的装配构型；从分支运动奇异、平台约束奇异和驱动奇异三个方面对机构进行了奇异分析；最后给定了一组尺寸参数，采用数值搜索的方法得到了机构的姿态工作空间。通过结果可以看出,该机构可以实现三维转动，具有较大的姿态工作空间，而且制造装配相对容易，具有很好的应用前景。

三自由度转动;并联机构;汇交轴线;奇异;姿态工作空间

0　引言

三自由度转动并联机构是十分重要的一类少自由度并联机构，在卫星跟踪随动装置、数控回转台等需要变换姿态的场合中具有广泛的应用前景。

传统的三自由度转动并联机构又称为球面并联机构。最典型的球面机构是Cox[1]在1981 年提出的3-RRR 并联机构，很多学者针对这种机构作了进一步的研究[2-5]。

近年来，各种不同的球面并联机构相继被提出。例如，Karouia等[6]设计的3-UPU球面并联机构，李秦川等[7]提出的3-PC(RR)N球面三自由度并联机构，Di Gregorio[8-10]设计的一类单环手腕机构，Valasek等[11]设计的含冗余约束的球面并联机构，赵云峰等[12]设计的含中间约束分支的3-UPS/S并联机构。一些学者对球面并联机构的型综合进行了相关研究[13-14]，并用不同的方法对球面并联机构作了深入的分析[15-21]。

然而，传统的三转动并联机构中往往含有多个空间汇交的运动副轴线，这种严格的几何条件给机构的加工制造带来很大的困难。一旦这种汇交关系没有得到满足，机构的运动性质就会发生改变。

Huang等[22]在1995年曾提出一种无汇交轴线的3-RPS并联角台机构，并在之后运用螺旋理论分析了各种角台式并联机构[23-24]。陈子明等[25]分析了两种三自由度并联角台机构的转动空间，并在此基础上进一步提出了这类无汇交轴线的三转动并联机构的型综合方法[26]。

本文介绍了一种无汇交轴线的三转动并联机构，并对其进行了运动学求解、转动空间计算以及奇异位形分析。

1　自由度分析

3-[RPR]RR三自由度转动并联机构如图1所示，机构由定平台、动平台以及三个相同的[RPR]RR分支构成。每个分支由转动副R1、移动副P2以及转动副R3、R4、R5依次连接构成。R1、R3相互平行，P2与R1、R3垂直，这三个运动副构成一个三自由度的平面子链[RPR]。转动副R4与R3相互垂直，转动副R5与R4相互垂直。R1与定平台倾斜连接，R5与动平台垂直连接。

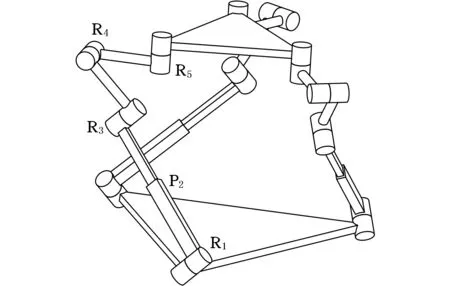
图1　3-[RPR]RR并联机构

如图2所示，在分支中建立一个局部坐标系oiuiviwi，坐标系的原点位于转动副R4的中心点，坐标轴ui沿分支转动副R4的轴线方向，坐标轴wi与分支第一个转动副R1的轴线平行，坐标轴vi的方向由右手定则确定。分支的运动螺旋系可以表示为

(1)

其中，d1、e1、d2、e2、d3、e3、b5、c5是与各转动副的方向和位置相关的量。

图2　[RPR]RR分支

根据分支运动螺旋系与约束螺旋系的关系可以求出分支的约束螺旋为

(2)

这个约束螺旋表示的是一个经过分支坐标系原点且平行于分支第一个转动副轴线的约束力。对于整个机构来说，三个分支一共对动平台施加了三个约束力。

利用修正的G-K公式，可以求得机构的自由度M=6(14-15-1)+15+0=3。

由于每个分支中的第一个转动副固连于定平台上，其轴线方向不会随机构的运动而发生变化,于是，各分支约束力的方向相对于定平台始终保持不变。对于整个机构，根据分支布置的对称性可知，动平台上一共施加有三个约束力,这三个约束力的方向均沿各分支的定平台转动副轴线方向。机构动平台始终受到空间交错的三个约束力，限制了动平台的三个移动自由度，动平台剩下三个转动自由度。

根据螺旋互逆原理，可以求得3-[RPR]RR机构动平台在这三个约束力作用下的运动螺旋系为一个一般的三阶螺旋系，其中既包含节距为零的纯转动,又包含节距为有限值的一般螺旋运动。这与传统的球面三自由度转动并联机构是不同的，球面三自由度转动并联机构能够实现绕定点的转动，而3-[RPR]RR机构动平台在转动过程中没有固定的转动中心。由于3-[RPR]RR机构动平台能够实现空间任意三维姿态，因而还是将其称作为三自由度转动并联机构。

2　位置反解及装配构型

2.1位置反解

机构坐标系的建立如图 3所示。定坐标系{B}与动坐标系{M}的原点分别设在定平台、动平台的中心点。定坐标系的X轴沿OA1方向，Z轴垂直于定平台。动坐标系的x轴沿PD1方向，z轴垂直于动平台。定平台、动平台的边长分别为la和lb。图3中，l34、l45分别为对应转动副间的连杆长度。

图3　机构坐标系的建立

在对机构进行反解时，机构动平台的姿态是已知的，其姿态矩阵可表示为

假设动平台中心点坐标为

P=[PXPYPZ]T

则动平台三个顶点在{M}中的坐标为

利用坐标系间的坐标变换公式，可得D1、D2、D3在{B}中的坐标为

(3)

(4)

(5)

定平台三个顶点在{B}中的坐标为

(6)

机构第i个分支中的5个运动副的螺旋可以分别表示为

(7)

其中,sij和rij分别为分支i中第j个运动副的轴线方向向量和空间位置向量，且

(8)

由于$i5的方向与动坐标系的z轴同向，因此其方向向量为

si5=(ax,ay,az)T

(9)

每个分支的第一个转动副固定在定平台上，且与定平台的夹角为α，如图4所示。以第一个分支为例，s11可以看作由一条与Y轴平行的直线绕X轴旋转α角而得到，即

其中，RX(α)表示绕X轴转动α角的旋转矩阵。

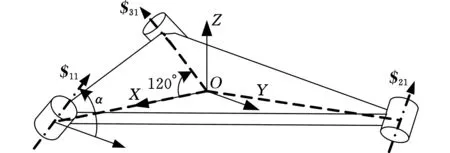
图4　定平台转动副

由于三个分支的第一个转动副关于Z轴对称分布，因此另外两个分支的$21和$31可以通过对$11进行旋转变换得到：

s21=RZ(120°)·s11

s31=RZ(-120°)·s11

每个分支中，$i1和$i3相互平行，有

si1=si3

由于$i4始终与$i3、$i5都保持垂直，因此

$i5已知，而$i4与$i5垂直，距离为杆长l45，可推导出$i4的位置向量为

(10)

同理，$i3始终与$i4垂直，距离为杆长l34，可推导出$i3的位置向量为

(11)

如图3所示，机构运动过程中，连杆l34始终垂直于$i1，所以有

(ri4-ri1)·si1=0

(12)

式中，ri1、si1为对应定平台转动副的位置向量和方向向量，为已知量。

联立式(5)～式(10)，可以得到ri4关于PX、PY、PZ的表达式。当i取1、2、3时，由式(12)可得到三个关于PX、PY、PZ的方程，从而得到P点绝对坐标。将PX、PY、PZ代入(10)、式(11)，即可求出ri4及ri3。

分支中移动副的方向矢量为

si2=ri3-ri1

至此，三个分支中的所有运动副的方向和位置都已经得到。

选取每个分支的移动副作为驱动副，则可以求得驱动杆的长度为

di=|ri3-ri1|

至此，就完成了机构的反解。根据式(10)、式(11)可知，每个分支在反解时都有四组解。

2.2装配构型

根据机构分支的四组反解，可以得到机构对应的四种对称的装配构型，如图5所示。

(a)装配构型1 　　　　 　　 (b)装配构型2

(c)装配构型3 　　　　 　　 (d)装配构型4图5　机构的四种装配构型

3　奇异分析

本文中对机构的奇异分析采用Fang等[27]的分类方法，并运用螺旋理论和线几何来判别机构的奇异位形。根据上述分类方法，并联机构的奇异可以分为三种：分支运动奇异(limb singularity)、平台约束奇异(platform singularity)和驱动奇异(actuation singularity)。

3.1分支运动奇异

在某些位形下，分支运动螺旋系产生线性相关时，机构输出构件自由度减少，称之为分支运动奇异。

观察式(1)，可以看到分支的运动螺旋系最后一列元素均为0，所以矩阵的秩仅取决于其前五列。取螺旋系前五列得到方阵A：

A=001d1e1000d2e2001d3e3100000b5c511éëêêêêêêùûúúúúúú

对方阵A进行分块，可以很容易得到A的行列式值为

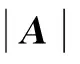
(1)当b5=0时，分支运动螺旋系可表示如下：

$i1=(001;d1e10)

$i2=(000;d2e20)

$i3=(001;d3e30)

$i4=(100; 000)

$i5=(00c5; 100)

通过观察，容易得到其约束螺旋系为

对比式(2)可以看出，此时分支约束螺旋系增加了一个约束力偶，所以发生这种奇异时，该分支会额外限制动平台的一个转动自由度。

b5=0时，$i5的方向向量变为(0,0,c5)，即与si1、si3平行。如图6所示，分支中后两个连杆间夹角γi=0°或者γi=180°时，分支中转动副R3与R5轴线平行，机构就会产生这种奇异。

(a)γi=0°　　　　　　(b)γi=180°图6　分支运动奇异

如图5所示，该机构四种装配构型中，构型1和构型2以及构型3和构型4的区别均在于转动副R4两端连杆的相对位置不同。当R4的转角为0°或180°时，R3和R5的轴线平行，转动副R5与平面子链中两个转动副产生线性相关，即发生图6所示的分支运动奇异。其中构型1和构型4较容易发生γi=180°的这种奇异，而构型2和构型3则较容易发生γi=0°的这种奇异。

3.2平台约束奇异

当机构的约束螺旋系发生线性相关时，动平台受到的约束减少，自由度增加，这种奇异称之为平台约束奇异。

对于3-[RPR]RR机构，每个分支对动平台施加一个约束力。由螺旋理论，只有当共面汇交于一点、共面平行或共轴时，这三个力线矢才会线性相关，如图7所示。

(a)共面汇交 　 (b) 共面平行　　 (c) 共轴图7　三个约束力线矢线性相关的条件

而对于本文分析的这个机构，其动平台受到的三个约束力分别与各分支的第一个转动副相平行，而每个分支的第一个转动副固连在定平台上且与定平台倾斜布置，所以这三个约束力在空间相互交错，不会发生图7所示的线性相关。也就是说，机构不存在这种奇异。

3.3驱动奇异

驱动奇异是指当所有驱动副锁住后，动平台仍保留未被约束掉的自由度。

如图8所示，当锁住3-[RPR]RR机构三个分支中的移动副后，机构分支可看作是一个4R支链。建立与图2中相同的分支坐标系oiuiviwi，则分支的运动螺旋系可以表示为

图8　[RR]RR分支约束力

由螺旋互易原理可知，一定存在两个线性无关且与这四个运动螺旋都相逆的反螺旋。

如图8所示，能够找到两条直线与分支中所有转动副轴线共面，其中一条与wi轴重合，另一条在平面P1内且过点E和点F。图8中，P1是$i1、$i3所在平面，E和F分别是$i4、$i5与平面P1的交点。根据螺旋理论，任意两个共面的线矢量一定互逆，所以，这两条直线所决定的两个线矢量一定与运动螺旋系中四个线矢量互逆，构成分支的约束螺旋系,可以表示为

由于每个线矢量表示一个约束力，所以三个分支对动平台一共施加六个约束力，则动平台的约束螺旋系可以表示为

如图9所示，六个约束力分别由六个矢量表示，它们分布在图9所示这六个不同的平面内。在一般位形下，这六个约束力线性无关，动平台能够由所选定的三个驱动完全控制，不发生奇异。

图9　动平台所受约束力

4　工作空间分析

对于三自由度转动并联机构的工作空间，主要研究的是其转动能力，为了能够直观地描述机构的运动姿态，这里采用Bonev等[28]提出的一种修正的欧拉角，即Tilt-and-Torsion(T&T)欧拉角。相比传统欧拉角，这种T&T欧拉角对机构三维转动的描述更加直观。

如图10所示，动平台由初始位形运动到图10所示位置的转动过程可以用三个欧拉角来描述：φ指示偏转轴线位置，θ表示偏转角大小，ψ表示自转角大小。

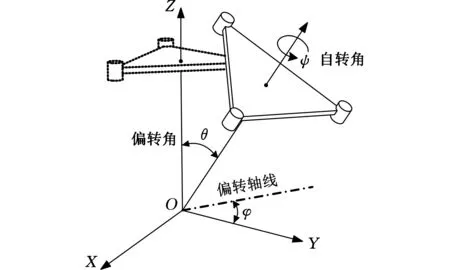
图10　T&T欧拉角

任意给定一组欧拉角，就可以得到机构此时的姿态矩阵。然后代入前面的反解计算，并按照所给定的约束条件进行判别，即可判断出所给的一组欧拉角是否在机构的转动空间内。在此基础上，按一定的规律搜索出三个欧拉角的变化范围，并将其范围在三维空间中表示出来，即得到机构的转动空间。这里采用圆柱坐标系来描述机构的转动空间，三个欧拉角(φ,θ,ψ)分别为圆柱坐标系的角度坐标、径坐标和竖坐标[25]。

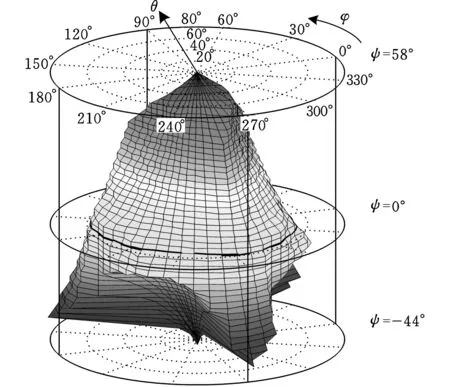
图11　机构转动空间

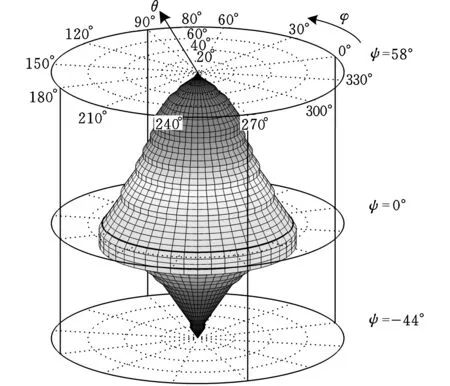
图12　转动空间的最大内切子空间

由图11可以看出：①机构的自转范围可达(-44°,58°)。②ψ在0°左右时，机构的偏转能力较大，动平台朝各个方向的最大偏转角约为θ=50°。

5　数值算例

这里给出机构工作空间内两个极限位置的算例，如表1所示，并通过三维模型进行了验证，如图13、图14所示。

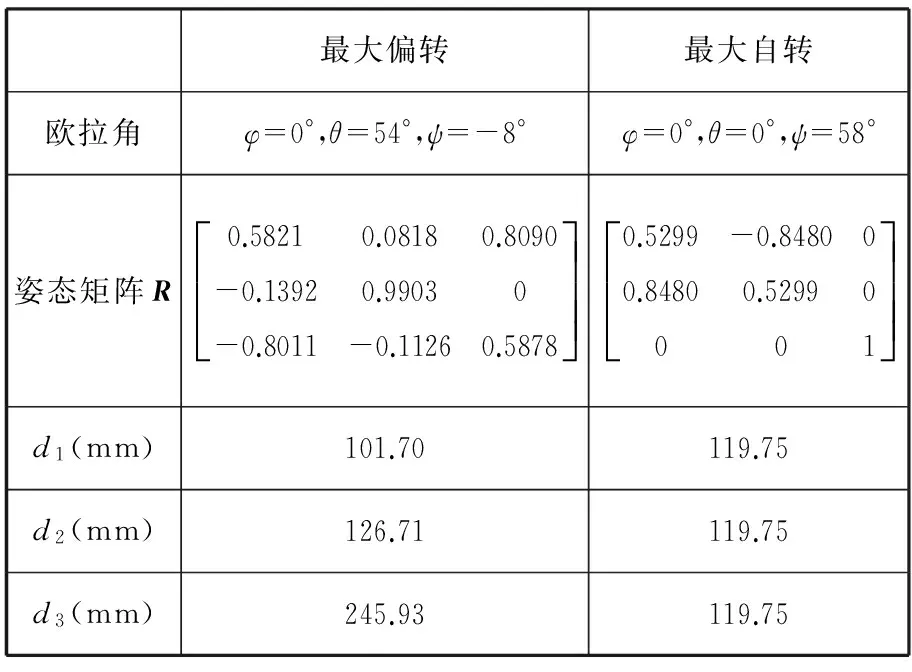
表1　数值算例

图13　最大偏转状态(φ=0°，θ=54°，ψ=-8°)

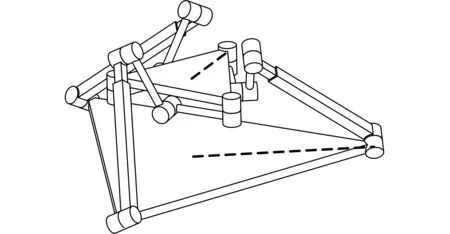
图14　最大自转状态(φ=0°，θ=0°，ψ=58°)

6　结论

(1)提出了一种3-[RPR]RR对称三自由度转动并联机构，该机构不存在空间汇交的运动副轴线，制造工艺相对简单。

(2)机构的动平台能够实现空间任意三维转动，但其自由度性质不同于传统的三自由度转动并联机构，其转动过程不存在固定的转动中心。

(3)机构的每个分支对应有四组反解，可以得到机构四种对称的装配构型。

(4)对机构进行了奇异性分析，结果表明,3-[RPR]RR机构不存在平台约束奇异，但存在分支运动奇异，当分支运动奇异发生时，机构的自由度会减少。

(5)由机构的工作空间分析可以看出，这种并联机构能够实现三维转动并具有较大的转动空间，在需要进行姿态控制的场合具有很好的应用前景。

[1]CoxDJ.TheDynamicModelingandCommandSignalFormulationforParallelMulti-parameterRoboticDevices[D].Gainesville,Florida:UniversityofFlorida, 1981.

[2]GosselinCM,HameiJ-F.TheAgileEye:aHigh-PerformanceThree-degree-of-freedomCamera-orientingDevice[C]//Proceedingsofthe1994IEEEInternationalConferenceonRoboticsandAutomation.SanDiego,CA,USA,1994: 781-786.

[3]杭鲁滨, 王彦, 吴俊, 等. 基于拓扑解耦准则的球面并联机构解耦条件研究[J]. 机械工程学报, 2005, 41(9):28-32.

HangLubin,WangYan,WuJun,etal.DecouplingConditionsofSphericalParallelMechanismBasedontheTopologicalDecouplingRules[J].ChineseJournalofMechanicalEngineering, 2005, 41(9): 28-32.

[4]张立杰, 刘辛军. 球面三自由度并联机器人可达工作空间的研究[J]. 中国机械工程, 2001, 12(10): 1122-1127.

ZhangLijie,LiuXinjun.ReachableWorkspaceAnalysisof3-DOFSphericalParallelMechanism[J].ChinaMechanicalEngineering, 2001, 12(10): 1122-1127.

[5]曾宪菁, 黄田, 曾子平. 3-RRR型数控回转台的精度分析[J]. 机械工程学报, 2001, 37(11):42-45.

ZengXianqing,HuangTian,ZengZiping.PrecisionAnalysisofthe3-RRRNCRotaryTable[J].ChineseJournalofMechanicalEngineering, 2001, 37(11): 42-45.

[6]KarouiaM,HerveJM.AThree-DOFTripodforGeneratingSphericalRotation[C]//AdvancesinRobotKinematics.Dordrecht:Springer, 2000: 395-402.

[7]李秦川, 陈欢欢, 李昳, 等. 3 -PC(RR)N球面三自由度并联机构的运动学分析[J]. 中国机械工程, 2009, 20(11):1280-1285.

LiQinchuan,ChenHuanhuan,LiDie,etal.KinematicAnalysisofaPC(RR)N3-DOFSphericalParallelMechanism[J].ChinaMechanicalEngineering, 2009, 20(11):1280-1285.

[8]DiGregorioR.SingularityAnalysisofaSingle-loopUnderactuatedWrist[C]//InternationalDesignEngineeringTechnicalConferencesandComputersandInformationinEngineeringConference.Portland,USA,2013:DETC2013-12044.

[9]DiGregorioR.PositionAnalysis,PathPlanning,andKinetostaticsofSingle-loopRu-(Ns)PuWrists[J].MechanismandMachineTheory, 2014, 74: 117-133.

[10]DiGregorioR.Single-loopWristsWhichGenerateTriangularStructures[J].MechanismandMachineTheory, 2014, 80: 230-245.

[11]ValasekM,ZichaJ,KarasekM,etal.Hexasphere-redundantlyActuatedParallelSphericalMechanismasaNewConceptofAgileTelescope[J].AdvancesinAstronomy, 2010: 348286.

[12]赵云峰, 程丽, 赵永生. 3-UPS/S并联机构运动学分析及机构优化设计[J]. 机械设计, 2009(1):46-49.

ZhaoYunfeng,ChengLi,ZhaoYongsheng,etal.KinematicAnalysisof3-UPS/SParallelMechanismandItsOptimizationDesign[J].JournalofMechanicalDesign, 2009(1): 46-49.

[13]FangY,TsaiL-W.StructureSynthesisofaClassof3-DOFRotationalParallelManipulators[J].IEEETransactionsonRoboticsandAutomation, 2004, 20(1): 117-121.

[14]KongX,GosselinCM.TypeSynthesisof3-DofSphericalParallelManipulatorsBasedonScrewTheory[J].JournalofMechanicalDesign, 2004, 126(1): 101-108.

[15]EnferadiJ,TootoonchiAA.AccuracyandStiffnessAnalysisofa3-RRPSphericalParallelManipulator[J].Robotica, 2011, 29(2): 193-209.

[16]BonevIA,ChablatD,WengerP.WorkingandAssemblyModesoftheAgileEye[C]//Proceedingsofthe2006IEEEInternationalConferenceonRoboticsandAutomation(ICRA2006) .Orlando,IEEE, 2006: 2317-2322.

[17]DiGregorioR.KinematicsofaNewSphericalParallelManipulatorwithThreeEqualLegs:the3-UrcWrist[J].JournalofRoboticSystems, 2001, 18(5): 213-219.

[18]BonevIA,GosselinCM.AnalyticalDeterminationoftheWorkspaceofSymmetricalSphericalParallelMechanisms[J].IEEETransactionsonRobotics, 2006, 22(5): 1011-1017. [19]BaiS,HansenMR,AngelesJ.ARobustForward-DisplacementAnalysisofSphericalParallelRobots[J].MechanismandMachineTheory, 2009, 44(12): 2204-2216.[20]BaiS.OptimumDesignofSphericalParallelManipulatorsforaPrescribedWorkspace[J].MechanismandMachineTheory, 2010, 45(2): 200-211.

[21]ZarkandiS.ANewGeometricMethodforSingularityAnalysisofSphericalMechanisms[J].Robotica, 2011, 29(7): 1083-1092.

[22]HuangZ,FangY.MotionCharacteristicsandRotationalAxisAnalysisofThreeDOFParallelRobotMechanisms[C]//IEEEInternationalConferenceonSystems,ManandCybernetics.Vancouver,British,1995: 67-71.

[23]黄真, 方跃法. 三自由度并联角台机构转轴存在的子空间[J]. 东北重型机械学院学报, 1997, 21(2):95-99.

HuangZhen,FangYuefa.SubspaceofExistingRotationAxisof3-DofCubicParallelMechanism[J].JournalofNortheastHeavyMachineryInstitute, 1997, 21(2): 95-99.

[24]HuangZ,ChenZ,LiuJ,etal.A3-DOFRotationalParallelManipulatorwithoutIntersectingAxes[J].JournalofMechanismsandRobotics, 2011, 3(2): 021014.

[25]陈子明, 陈谊超, 杨凤霞, 等. 两种三自由度并联角台机构的转动空间分析[J]. 机械工程学报, 2014, 50(5):48-56.

ChenZiming,ChenYichao,YangFengxia,etal.RotationWorkspaceAnalysisofTwo3-DOFCubicParallelMechanisms[J].ChineseJournalofMechanicalEngineering, 2014, 50(5): 48-56.

[26]ChenZ,CaoW,HuangZ.TypeSynthesisof3-DofRotationalParallelMechanismswithNoIntersectingAxes[C]//ASME2012InternationalDesignEngineeringTechnicalConferencesandComputersandInformationinEngineeringConference.Chicago, 2012:DETC2012-70846.

[27]FangY,TsaiL-W.StructureSynthesisofaClassof4-Dofand5-DofParallelManipulatorswithIdenticalLimbStructures[J].TheInternationalJournalofRoboticsResearch, 2002, 21(9): 799-810.

[28]BonevIA,RyuJ.ANewApproachtoOrientationWorkspaceAnalysisof6-DofParallelManipulators[J].MechanismandMachineTheory, 2001, 36: 15-28.

(编辑苏卫国)

Kinematics Analysis of a 3-DOF Symmetrical Rotational Parallel Mechanism without Intersecting Axes

Chen Ziming1,2Huang Kun1,2Zhang Yang1,2Ding Huafeng3Huang Zhen1,2

1.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System, Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of Education, Yanshan University, Qinhuangdao, Hebei, 066004 3.China University of Geosciences, Wuhan, 430074

The traditional 3-DOF rotational PMs also called as spherical parallel mechanisms(SPMs) usually had a rotation center which was the intersecting point of multiple revolute joint axes. This strict geometric conditions were very hard to fulfill in the manufacture processes and would restrict further applications of this kind of mechanisms. Thus, a PM with three rotational DOF and no intersecting axes was designed herein. It consisted of three identical limbs distributed symmetrically without intersecting axes in or between limbs. The inverse kinematics was solved and four symmetrical assembly modes were obtained. Then the singularity of the mechanism was analyzed and classified into three types: limb singularity, platform singularity and actuation singularity. At last, its orientation workspace was studied. This mechanism can realize three dimensional rotations with large workspace and is easier for manufacturing and assembly, so it has broad application prospects.

3-DOF rotation; parallel mechanism(PM); intersecting axes; singularity; orientation workspace

2015-07-07

国家自然科学基金资助项目(51305381)；高等学校博士学科点专项科研基金资助项目(20131333120006)

TH112

10.3969/j.issn.1004-132X.2016.09.013

陈子明，男，1984年生。燕山大学机械工程学院讲师、博士。主要研究方向为少自由度并联机构的设计和分析。发表论文20余篇。黄坤，男，1992年生。燕山大学机械工程学院硕士研究生。张扬，男，1988年生。燕山大学机械工程学院硕士研究生。丁华锋，男，1977年生。中国地质大学机械与电子信息学院教授、博士研究生导师。黄真，男，1936 年生。燕山大学机械工程学院教授、博士研究生导师。