滚齿机复合材料滑动导轨磨损性能

李先广　杨　勇

重庆机床(集团)有限责任公司，重庆，401336



滚齿机复合材料滑动导轨磨损性能

李先广杨勇

重庆机床(集团)有限责任公司，重庆，401336

为了掌握滚齿机复合材料滑动导轨磨损性能，在振动爬行原理、Reynolds理论及复合材料滑动导轨工况参数的基础上，建立了复合材料滑动导轨稳定磨损阶段的磨损深度随磨损时间变化关系模型，提出了磨损深度测试方案，成功研制出复合材料滑动导轨磨损测试试验机。运用滚齿机复合材料滑动导轨样件进行了磨损试验，分析了复合材料滑动导轨磨损深度的试验与理论数据，揭示了复合材料滑动导轨磨损规律。理论数据与试验数据相比较，两者相对误差低于5%，验证了理论研究的正确性，表明该研究可为滚齿机复合材料滑动导轨的油槽结构、油槽几何参数及油膜承载能力的优化设计与导轨选型提供有益参考。

滚齿机；复合材料；滑动导轨；磨损率；磨损深度

0　引言

机床导轨摩擦磨损对导轨性能、寿命及机床加工精度与性能有着重要影响[1-5]。滚齿机复合材料滑动导轨工作载荷大、工况复杂，导轨更换难度大且成本高，故展开滚齿机复合材料滑动导轨磨损性能研究，对大型机床导轨维护与油槽结构参数优化设计极为重要。

近年来，国内外学者对导轨摩擦磨损进行了大量研究，如李皓[6]的研究表明，淬火钢导轨耐磨性较普通铸铁导轨耐磨性有很大提高；王承鹤等[7-8]对聚四氟乙烯基复合材料滑动导轨软带在金属切削机床上的应用及其摩擦与磨损机理进行了研究，指出聚四氟乙烯基复合材料滑动导轨软带的应用可以极大地提高导轨耐磨性能；Pal等[9]对塑料导轨在机床上的应用进行了研究，利用试验数据得到了塑料导轨磨损经验公式；Khedkar等[10]对PTFE复合材料中各种添加剂对导轨材料抗磨损性能的影响进行了试验研究；Chauhan等[11]对乙烯基材料在干摩擦以及水润滑滑动摩擦条件下的磨损行为进行了试验研究，指出添加了玻璃纤维(GFR)乙烯基复合材料的磨损率随法向载荷的增大而减小。

由于摩擦磨损问题较为复杂，国内外学者对此开展了大量有效的研究工作，也取得了许多丰硕的研究成果[12-20]，但目前专门针对滚齿机复合材料滑动导轨磨损性能方面的研究仍鲜见报道，其磨损规律尚不清楚，在工程实际中，机床复合材料滑动导轨的设计主要是依靠经验。为了揭示滚齿机复合材料滑动导轨磨损规律，本文根据振动爬行原理、Reynolds理论及复合材料滑动导轨的实际工况参数，建立了复合材料滑动导轨磨损深度随磨损时间变化的关系模型，提出了磨损深度测试方案，并成功研制了复合材料滑动导轨磨损测试试验机；运用滚齿机复合材料滑动导轨样件进行了磨损试验测试，将复合材料滑动导轨磨损深度试验测试值与理论计算数据进行了对比分析。

1　滚齿机复合材料滑动导轨相对滑动速度公式

滚齿机大立柱移动时，在其复合材料滑动导轨(滚齿机实际结构中，采用1.2 mm厚的聚四氟乙烯基复合材料与大立柱导轨槽紧紧镶贴在一起构成滑动导轨)与静压导轨(20CrMnTi材料的静压导轨是固定安装在床身上的，在机床加工过程中固定不动)间将产生滑动接触摩擦(图1)，主要原因是立柱导轨槽中有循环润滑油槽，机床工作过程中滑动导轨在静压导轨上移动时，在滚齿切削载荷和立柱重力的共同作用下，油槽中的循环润滑油便在静压导轨面上形成动压润滑油膜，故滑动导轨与静压导轨间会产生滑动接触摩擦；但如果机床立柱导轨槽中没有循环润滑油，那么滑动导轨与静压导轨间将出现干摩擦，不仅使滑动导轨在静压导轨上的移动阻力增大，而且会快速加剧机床导轨的磨损。因此，在滑动导轨与静压导轨间需要具备形成动压润滑的条件，而且这是必要的。

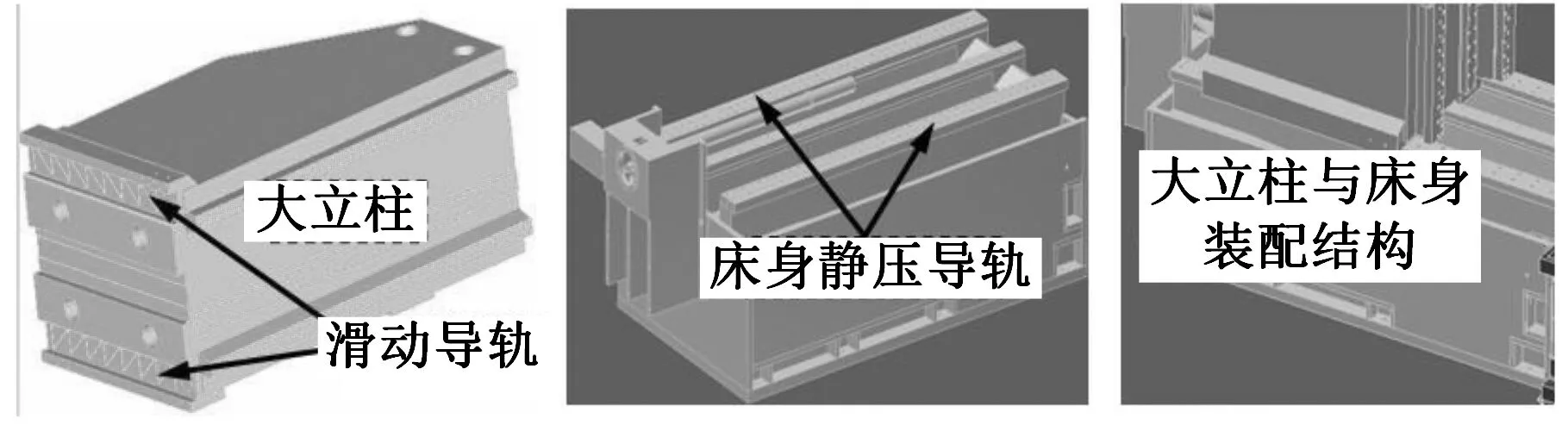
图1　滚齿机滑动与静压导轨简图

当滑动导轨出现低速范围移动时，大立柱会出现摩擦力急剧减小的现象，在摩擦力减小的速度特性下，大立柱将出现振动、不稳定运动及跳跃式爬行运动等现象[21-22]，从而影响滚齿机几何精度，严重时会造成机床结构破坏[23]，因此，需对大立柱复合材料滑动导轨的磨损现象进行研究。将大立柱复合材料滑动导轨的实际进给系统进行简化，如图2所示。

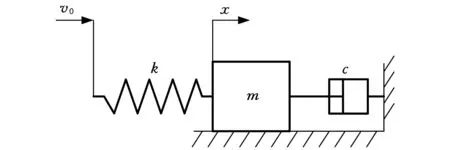
图2　系统简化模型

当滚齿机复合材料滑动导轨的相对运动速度很低时，由图2可知，动静导轨间的实际进给系统微分方程为

(1)

式中，k为系统刚度；v0为系统速度；x0为开始运动时的弹簧压缩量；c为阻尼系数；c0为摩擦力随速度变化的系数；F0为摩擦力的恒定部分；t为时间；m为简化系统质量。

当弹簧压缩x0后，系统开始运动，取kx0=Fs0，其中，Fs0为静摩擦力。令Fs0-F0=ΔF，则式(1)可写成

(2)

为了方便求解该二阶非齐次微分方程，将式(2)改写为

(3)

通常，复合材料滑动导轨系统阻尼比(为常量)ζ≪1，故式(3)有一对共轭复根，其通解为

X(t)=e-ζωnt(C1cosωdt+C2sinωdt)

(4)

其中，0不是齐次方程特征方程的根，则对应的特解为

x*(t)=b0t+b1

(5)

将式(5)代入式(3)，可得

(6)

则式(2)的解为

x(t)=X(t)+x*(t)=v0t+

(7)

(8)

将式(8)代入式(7),有

(9)

由式(9)可知，复合材料滑动导轨的滑动速度v为

(10)

当系统阻尼比ζ≪1时，ζ2=0，则式(10)可简化为

(11)

将式(11)转化为

v=v0-v0e-ζωntAsin(ωnt+θ)

(12)

式中，A为滑动速度的振动分量的振幅；θ为相位角。

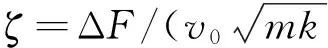
v=v0(1-e-ζωnt)

(13)

2　滚齿机复合材料滑动导轨摩擦副表面压力分析

根据Reynolds理论，复合材料滑动导轨表面油槽结构与尺寸对导轨摩擦磨损有很大影响，在机床滚齿加工过程中，复合材料滑动导轨与静压导轨的接触面之间形成一层很薄的油膜，在重负荷下作用产生动压油膜，使两导轨表面不相互直接接触，从而可大幅减小导轨摩擦磨损。图3为某滚齿机复合材料滑动导轨的部分油槽结构简图，图4为图3虚线处的截面示意图。

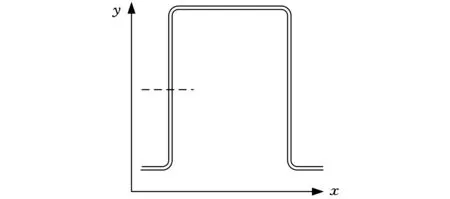
图3　滚齿机复合材料滑动导轨部分油槽结构分布简图

图4　虚线(图3)处的截面示意图

为了解复合材料滑动导轨油槽结构对导轨动压油膜及承载能力的影响，Rayleigh曾用变分法分析了不同形式滑块的动压承载能力，发现图4 所示阶梯滑块结构的油槽截面，其油膜具有较大承载能力，导轨油膜承载力为[24]

(14)

其中，S为导轨横截面宽度；U为动静导轨间的相对运动速度(由于滚齿机加工过程中，静压导轨是固定不动的，故动静压导轨间的相对运动速度U便等于滑动导轨的滑动速度v，即U=v)；η为润滑油黏度。为了使润滑液体产生动压油膜，h2与导轨表面粗糙度之间必须满足下式[25]：

(15)

其中，Rq1、Rq2分别为两导轨接触面摩擦副的表面粗糙度，Rq1=1.6μm，Rq2=3.2μm。由式(15)计算得h2>10.74μm，则取h2≥10.74μm。

为了提高动压油膜的承载能力，必须合理设定B1/B2与h1/h2的值，故将式(15)变换为以下形式：

(16)

B=B1+B2Q=B2/Bq=h1/h2

(17)

(18)

求解式(17)，有

(19)

求解式(18)，有

(20)

由式(19)与式(20)有，只有当式(19)取第一个解、式(20)取第三个解时，联立式(19)与式(20)求解q才能得到有意义的解，即

(21)

由式(21)解得q=1.866，则q=h1/h2=1.866，Q=B2/B=0.282，B1/B2=2.546。满足上述条件时，动压油膜的最大承载能力为

(22)

由此可得滚齿机复合材料滑动导轨摩擦副接触面的最大表面压力：

(23)

A1=S(B1+B2)

式中，A1为复合材料滑动导轨摩擦副接触面积。

3　重负荷下复合材料滑动导轨磨损机理分析

在滚齿机工作中，大立柱动静导轨不可能处于纯液体润滑状态，实际导轨表面是由微观上凹凸不平峰谷组成的，如图5所示。

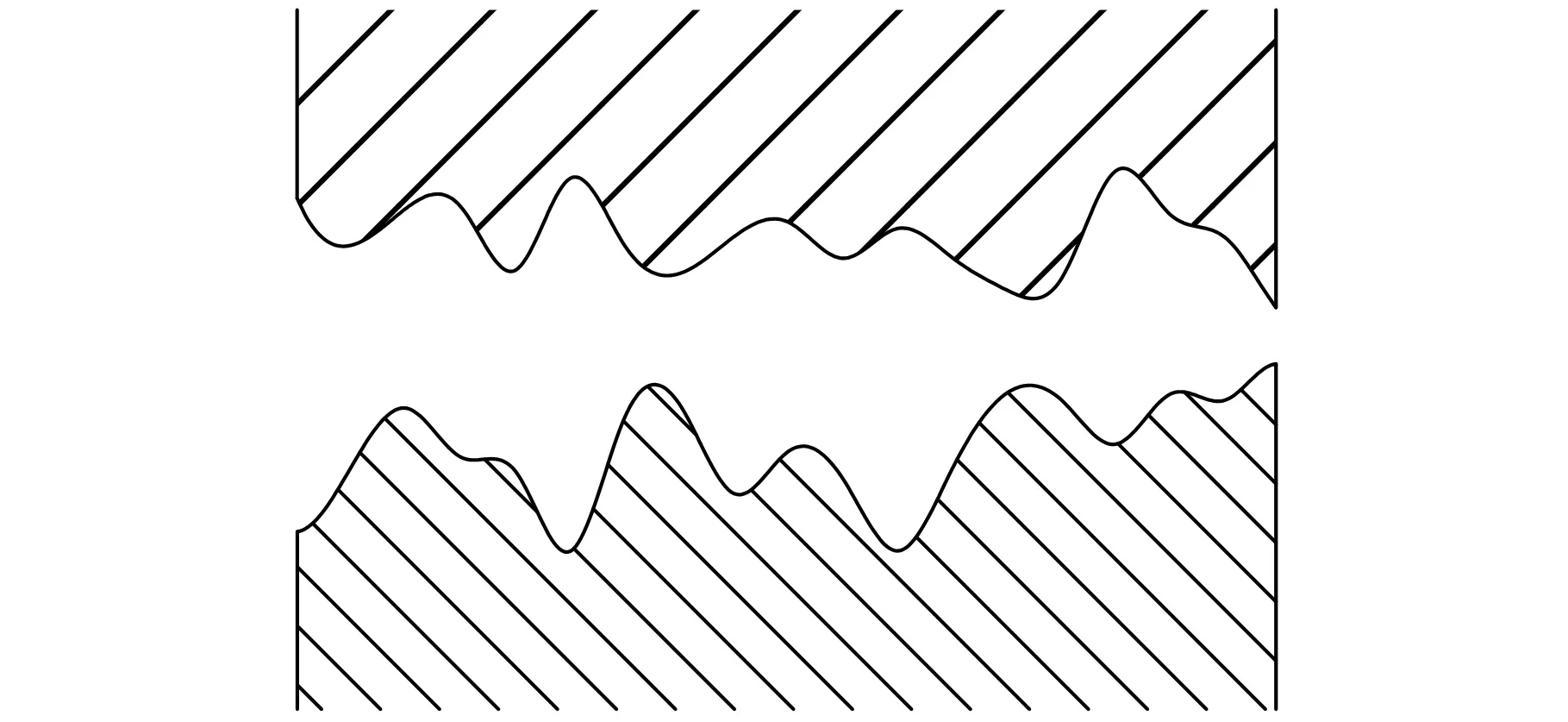
图5　动静导轨实际接触表面示意图

从导轨表面微观上看，实际是存在图5所示的峰谷形状，两导轨表面摩擦副实际并未完全接触，润滑油在未接触表面形成不规则油楔，根据Reynolds理论，当油楔收敛方向与两导轨相对运动方向相反时，即可产生一定动压效应和挤压效应，该部分液体压力在一定程度上减小了两导轨之间的接触压力，可减缓导轨磨损。另外，滚齿机工作时其导轨上不可避免会落有金属切屑，大立柱移动时，金属将对导轨表面产生磨损刮伤。

复合材料滑动导轨摩擦磨损影响因素多且复杂，但在导轨摩擦副的稳定磨损阶段，磨损深度h主要与摩擦副表面压力p、滑动速度v及磨损时间t有关，即

h=Kpmvnt

(24)

式中，K为摩擦工况条件系数，与摩擦副材料、表面品质和润滑状态等因素有关；m为表面压力对磨损率的影响指数；n为滑动速度对磨损率的影响指数。

将式(13)与式(23)代入式(24)可得，滚齿机复合材料滑动导轨摩擦副在稳定磨损阶段的磨损深度h为

(25)

4　复合材料滑动导轨磨损试验

4.1磨损试验机

为了掌握滚齿机复合材料滑动导轨磨损性能与提高其重负荷下的抗磨能力，专门研制了一台磨损试验机，如图6所示，该装置一次性可对12个复合材料滑动导轨样件在12种不同的压力与滑动速度组合下进行磨损试验。

图6　导轨摩擦磨损试验装置

试验时，样件安装在加载支架的加载管中，采用弹簧施加压力载荷，样件的磨损面垂直紧压接触在圆盘导轨(相当于滚齿机床上的静压导轨，用20CrMnTi材料制成)面上，圆盘导轨可绕其自身轴转动，利用变频电机驱动圆盘导轨转动，使复合材料滑动导轨样件在圆盘导轨上进行磨损。

磨损率中的工况系数K及影响指数m、n与摩擦副材料、表面粗糙度、润滑油品种等因素有关，为了准确获取这些参数值，将实际应用于滚齿机上的复合材料滑动导轨样件在多组压力和滑动速度下进行磨损试验。磨损试验采用32号机械润滑油，磨损样件为聚四氟乙烯基复合材料滑动导轨，试验条件见表1。

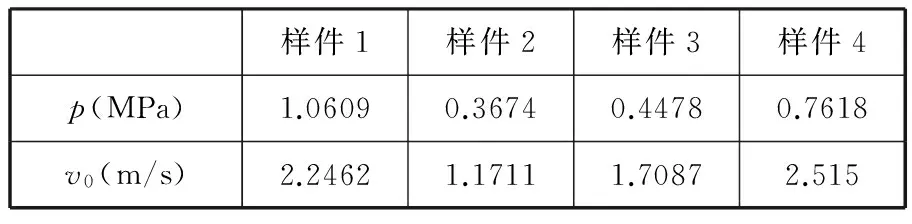
表1　磨损试验条件

将得到的多组数据运用数值方法拟合得到参数K、m及n的值，见表2。

表2　复合材料滑动导轨磨损相关参数

4.2磨损试验样件及磨损形貌分析

在滚齿机实际结构中，聚四氟乙烯基复合材料(主要为聚四氟乙烯基铜复合材料)与大立柱导轨槽(导轨槽中开有油槽)紧紧镶贴在一起构成滑动导轨，为了使试验达到实际效果，在磨损试验机中，将聚四氟乙烯基复合材料样件加工成厚1.2 mm、直径为18 mm的圆柱片，通过环氧树脂胶粘贴到加载支架的加载管上构成滑动导轨(图7)。试验滑动导轨安装在加载支架(图6)上，试验过程中圆盘导轨(图8)绕磨损试验机主轴旋转，加载支架按实际工况对滑动导轨样件进行轴向加载，使滑动导轨样件始终与圆盘导轨底面接触从而保持摩擦磨损状态，磨损试验连续进行21 h。

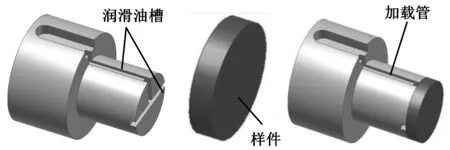
图7　磨损试验样件及安装示意图

图8　磨损试验机内部结构及圆盘导轨

图9所示为滑动导轨聚四氟乙烯基铜复合材料样件磨损前的实物及放大50倍形貌，图10所示为磨损后的实物及放大50倍磨损形貌。由图9与图10可知，磨损前聚四氟乙烯基铜复合材料样件表面呈现较小的凹凸不平情况，并且表面组织的形貌颗粒粗大、分布不均匀；磨损后样件表面比较平整与光洁，并且表面组织的形貌颗粒变得细小且分布均匀。另外，样件磨损深度采用光栅位移传感器(测量精度为0.1 μm精度等级)进行测量，在样件被磨损的圆面上均匀取24个点进行测量，将测量值进行加权平均作为样件最终的磨损深度值。

图9　磨损前滑动导轨实物样件及放大50倍磨损形貌图

图10　磨损后滑动导轨实物样件及放大50倍磨损形貌图

4.3磨损试验数据分析

由图11可知，滚齿机复合材料滑动导轨试验样件的磨损由较剧烈变化的初期阶段和磨损相对平稳的稳定上升阶段组成，在0～9.4167 h间，曲线随磨损时间呈上拱抛物线变化，即初期磨损阶段，初期磨损的磨损率均大于稳定阶段磨损率；在9.4167 h后曲线为磨损稳定上升阶段，样件磨损深度与时间呈线性上升变化趋势。由于试验样件截面与形状切取不均匀，大小各不相同，使得图7中样件的磨损深度相差较大，且磨损深度还与接触表面压力与滑动速度有关，即表面压力与滑动速度越大，磨损量越大。

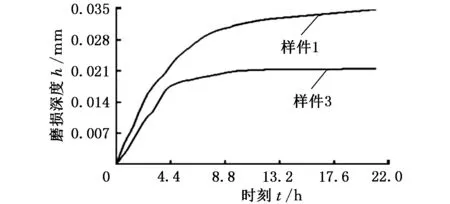
(a)样件1、3

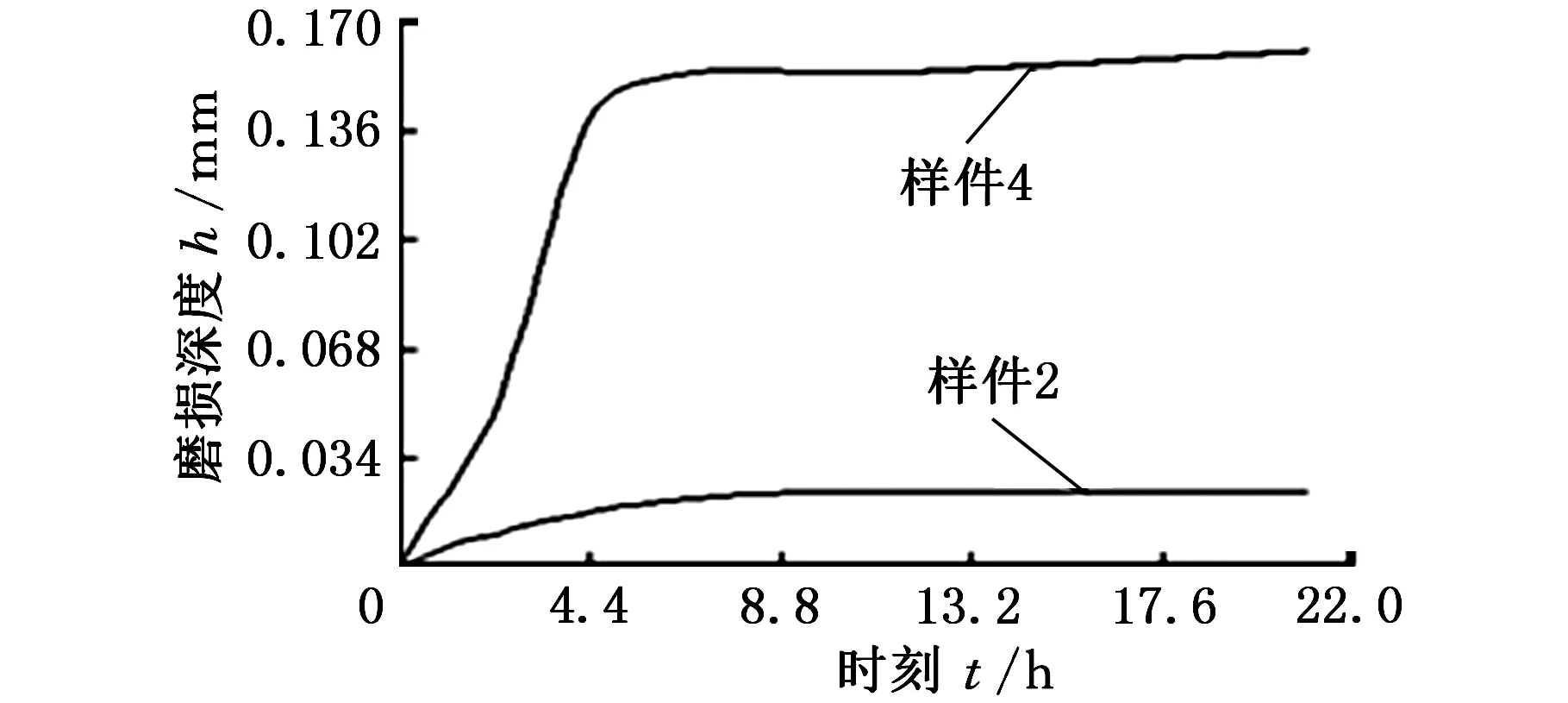
(b)样件2、4图11　复合材料滑动导轨样件磨损深度试验测试数据曲线

试样初期的磨损率大于后期的磨损率，主要原因是试样实际表面粗糙度较大(图5)，样件表面由凹凸不平的波峰构成，并非理想平面，磨损初期样件表面粗糙度相对较大，样件与静压导轨的实际接触面均为少数凹凸不平的波峰，在载荷作用下产生塑性变形而形成的接触面，实际接触面积小于名义接触面积，使实际加载比压大于名义比压，从而使得样件初期阶段磨损比较剧烈，如图11所示。当样件磨合一段时间后，表面上凹凸不平的波峰被磨平，样件的实际接触面积增大，其磨损率逐渐减小，进入稳定磨损阶段，这说明导轨表面的加工质量对磨损率有较大影响，导轨表面质量越好，磨合的时间越短。

在实际应用时，通常仅关注复合材料滑动导轨稳定磨损阶段的磨损量，故为了简化理论研究，本文仅进行了稳定磨损阶段的理论计算，由式(25)与表1、表2参数值可计算出复合材料滑动导轨稳定磨损阶段的磨损深度数据，如图12～图17所示。由图11试验数据可知，样件进入稳定磨损阶段的时间约在9.4167～21 h间，为了方便理论与试验值的比较分析，将图11中样件稳定磨损阶段的试验数据单列出来，如图12～图17所示(图12～图17是样件磨损到达稳定阶段以后的绝对磨损量数据曲线，而达到稳定阶段的起始时刻为9.4167 h)。

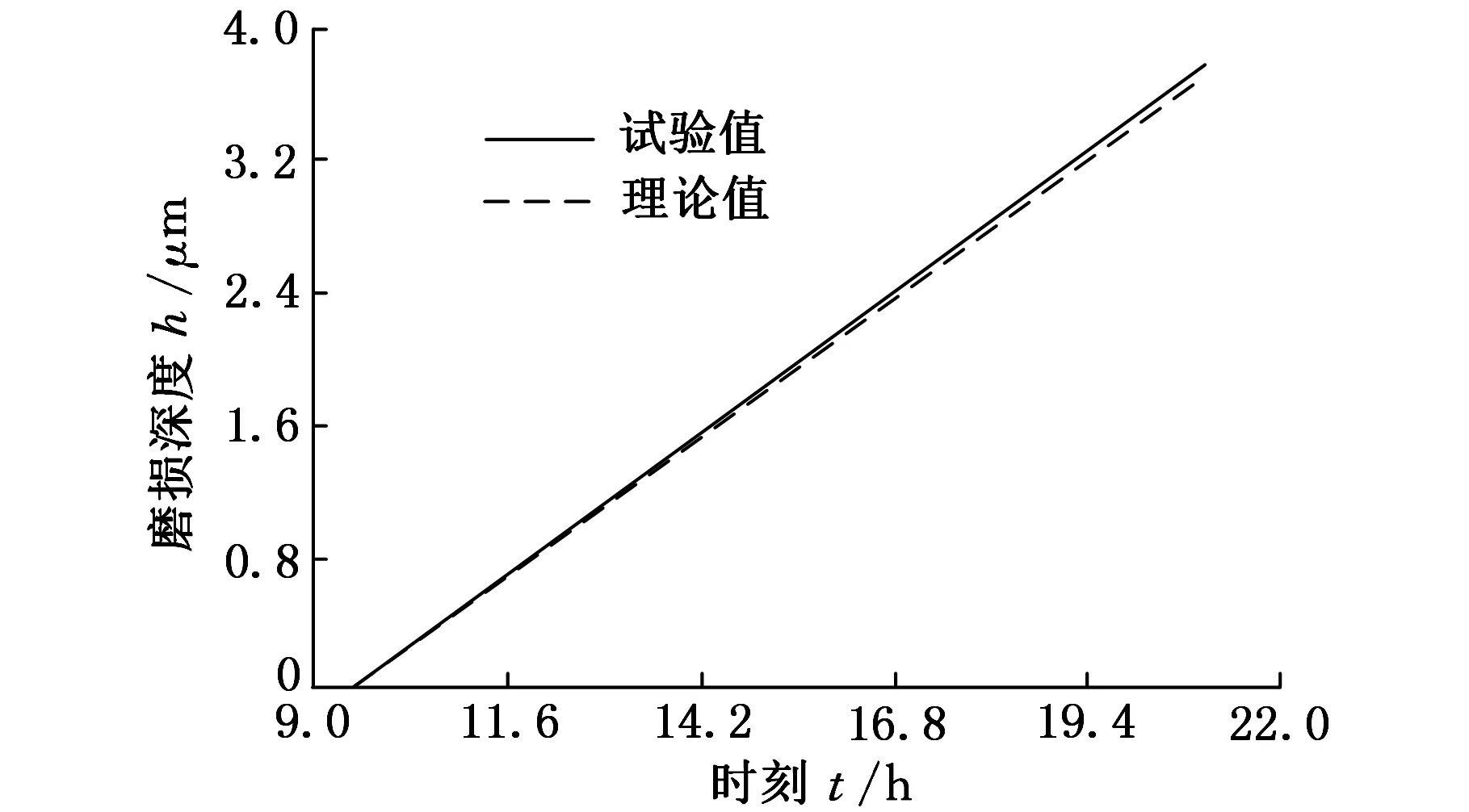
图12　样件1磨损深度-时间变化曲线

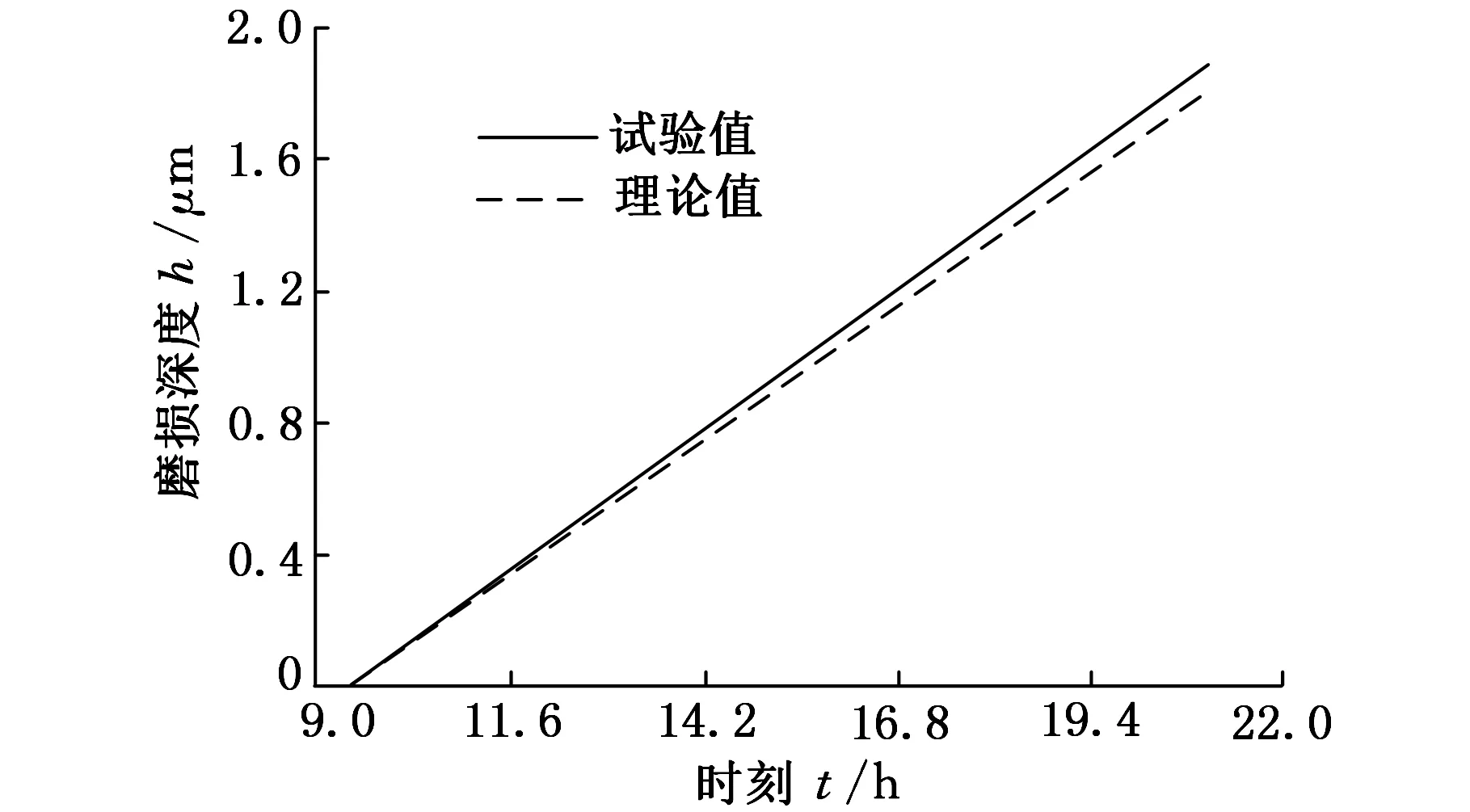
图13　样件2磨损深度-时间变化曲线

图14　样件3磨损深度-时间变化曲线

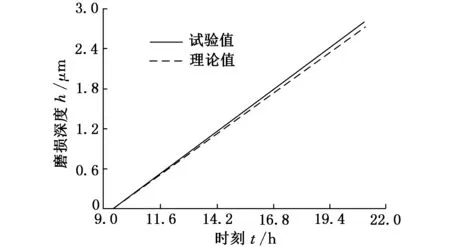
图15　样件4磨损深度-时间变化曲线

图16　试验测试样件磨损深度与时间变化曲线

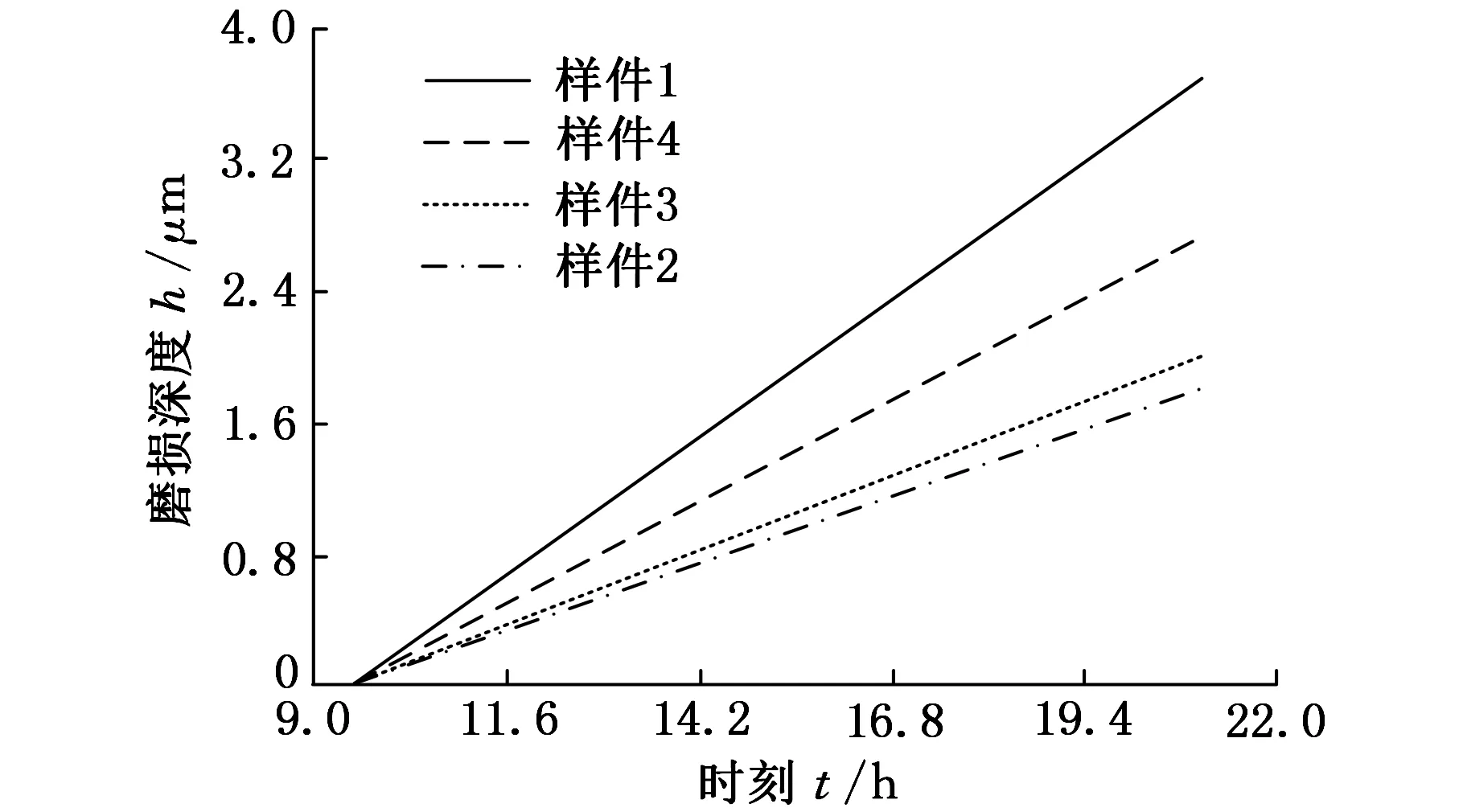
图17　理论计算样件磨损深度与时间变化曲线

由图12～图17可知，在稳定磨损阶段的12 h内，样件磨损深度的试验值与理论值变化规律均相同，磨损深度随磨损时间的增加而增长且呈线性上升变化，其主要原因如下：①样件在外界加载工况挤压下，聚四氟乙烯基复合材料样件表平面由较小凹凸不平情况逐渐变得平整与光洁，且样件材料内部晶粒组织由疏松逐步变得紧密，当样件磨损到一定程度时，随着磨损时间增加，磨损量越来越小，且出现趋于平稳现象(图11)；②由于磨损加载是按实际工况进行添加的，即在机床加工过程中，随着时间推移，切削载荷与机床特性逐渐趋于稳定，使得加载到样件上的负荷也趋于线性均匀变化与稳定状态，故当滑动导轨样件在静压导轨移动时，滑动导轨样件磨损量随着磨损时间增长变化较小，且呈线性关系变化状态。并且由图16、图17可知，磨损深度随滑动速度与表面压力的增大而增大，图16、图17中样件1的表面压力与滑动速度较大，磨损深度最大，试验值约3.793 μm，理论值约3.726 μm；样件2的表面压力与滑动速度较小，磨损深度最小，试验值约1.893 μm，理论值约1.818 μm；根据图12～图15，试验数据均略大于理论数据，但两者的相对误差均低于5%，试验数据偏大的主要原因是在样件磨损试验中，在振动与压力作用下样件发生变形并产生样件磨损深度的测量误差。

5　结论

(1)根据滚齿机复合材料滑动导轨实际工况及性能参数，建立了稳定磨损阶段条件下的磨损深度随磨损时间变化的关系模型，通过该模型可直接计算复合材料滑动导轨稳定磨损阶段的磨损深度数据，揭示了复合材料滑动导轨稳定磨损阶段磨损的理论规律。

(2)结合理论研究与实际工况的需要，研制出一台滚齿机复合材料滑动导轨摩擦磨损试验机，提出了复合材料滑动导轨磨损试验方案，通过试验得到了复合材料滑动导轨磨损深度试验数据，经稳定磨损阶段的试验与理论数据分析对比可知，两者相对误差低于5%，揭示了复合材料滑动导轨稳定磨损阶段磨损的实际规律，验证了理论研究的正确性。

(3)由理论与试验研究可知，滚齿机复合材料滑动导轨的磨损由较剧烈变化的初期阶段与相对平稳上升的稳定阶段组成，磨损深度随磨损时间的增加呈直线上升，并随滑动速度与表面压力的增加磨损深度越大，且复合材料滑动导轨油槽截面结构参数与导轨表面加工质量对磨损率有着重要影响。研究结果可为滚齿机大立柱导轨槽的油槽结构、油槽几何参数、油膜承载能力优化设计，以及导轨与复合材料选型提供有益的参考。

[1]Meng Yonggang, Hu Bo, Chang Qiuying. Control of Local Friction of Metal/ceramic Contacts in Aqueous Solutions with an Electrochemical Method[J]. Wear, 2006, 260(3):305-309.

[2]Davim J P, Cardoso R. Effect of Reinforcement (Carbon or Glass Fibre) on Friction and Wear Behavior of the PEEK against Steel Surface at Long Dry Sliding[J]. Wear, 2009, 266(7): 795-799.

[3]Xi Xuecheng,Poo A N,Hong G S.Tracking Error-based Static Friction Compensation for a Bi-axial CNC Machine[J]. Precision Engineering, 2010，34(3): 480-488.

[4]陈光胜, 梅雪松, 陶涛.X-Y工作台摩擦误差补偿方法的研究[J].西安交通大学学报, 2011,45(1): 69-73.

Chen Guangsheng, Mei Xuesong, Tao Tao. Compensation of Friction Error forX-YTable[J]. Journal of Xi’an Jiaotong University, 2011, 45(1): 69-73.

[5]冯斌, 梅雪松, 杨军, 等. 数控机床摩擦误差自适应补偿方法研究[J].西安交通大学学报, 2013,47(11):65-69.

Feng Bin, Mei Xuesong, Yang Jun,et al. Adaptive Compensation of Friction Error for Numerical Control Machine Tool[J].Journal of Xi’an Jiaotong University, 2013, 47(11):65-69.

[6]李皓. 淬火钢导轨的耐磨性能及其应用[J]. 中国设备工程, 2006, 11(1): 21.

Li Hao. Quenching Steel Guideway of Abrasion Resistance and Application[J].China Plant Engineering, 2006, 11(1):21.

[7]王承鹤,任杰. 聚四氟乙烯基复合材料滑动导轨软带在金属切削机床上的应用及其摩擦与磨损机理的研究——(一)干摩擦[J]. 西安理工大学学报, 1981, 6(2): 26-37.

Wang Chenghe, Ren Jie. Application on the Metal Cutting Machine Tool of Sliding Guideway Soft Belt of PTFE Composites and Research on Mechanism of Friction and Attrition-Dry Friction[J]. Journal of Xi’an University of Technology, 1981, 6(2): 26-37.

[8]王承鹤,任杰. 聚四氟乙烯基复合材料滑动导轨软带在金属切削机床上的应用及其摩擦与磨损机理的研究——(二)纯油摩, (三)油磨料摩擦(续前)[J].西安理工大学学报, 1981, 6(3): 44-56.

Wang Chenghe, Ren Jie. Application on the Metal Cutting Machine Tool of Sliding Guideway Soft Belt of PTFE Composites and Research on Mechanism of Friction and Attrition-Pure Oil and Oil Abrasive Materials Friction[J].Journal of Xi’an University of Technology, 1981, 6(3): 44-56.

[9]Pal D K, Basu S K. Wear Analysis of Plastic Guides Used in Machine Tools[J]. Wear, 1972, 21(1):1-7.

[10]Khedkar J, Negulescu I, Meletis E I.Sliding Wear Behavior of PTFE Composites[J]. Wear, 2002, 252(5/6): 361-369.

[11]Chauhan S R, Kumar A, Singh I.Sliding Friction and Wear Behaviour of Vinylester and Its Composites under Dry and Water Lubricated Sliding Conditions[J]. Materials & Design, 2010, 31(6): 2745-2751.

[12]卓耀彬,周晓军.高速滚珠关节轴承的动力学特性分析[J]. 机械工程学报,2015,51(5):37-46.

Zhuo Yaobin, Zhou Xiaojun. Dynamic Characteristic Analysis of High-speed Spherical Ball Bearing[J]. Journal of Mechanical Engineering, 2015, 51(5):37-46.

[13]刘建, 张永振, 杜三明, 等. 聚四氟乙烯编织复合材料摩擦温度与磨损特性[J]. 机械工程学报, 2012, 48(23): 90-94.

Liu Jian, Zhang Yongzhen, Du Sanming, et al.Temperature and Friction Characteristics of PTFE Braided Composites[J]. Journal of Mechanical Engineering, 2012, 48(23): 90-94.

[14]邱明, 吕桂森, 占松华, 等. 自润滑杆端关节轴承的摩擦性能研究[J]. 兵工学报，2013，34(6)：754-758.

Qiu Ming, Lü Guisen, Zhan Songhua, et al.Tribological Properties of Self-lubricating Rod Endspherical Plain Bearings[J]. Acta Armamentarii, 2013,34(6):754-758.

[15]李晓贞,朱如鹏,李政民卿,等. 齿面摩擦对面齿轮传动系统振动特性的影响分析[J]. 振动工程学报, 2014, 27(4):583-588.

Li Xiaozhen, Zhu Rupeng, Li Zhengminqing, et al. Influences of Frictional Coefficient on Vibration Characteristic of Face-gear Transmission System[J]. Journal of Vibration Engineering, 2014, 27(4): 583-588.

[16]张靖, 陈兵奎, 康传章,等. 齿面摩擦的直齿轮动力学分析[J]. 振动与冲击, 2012,31(21):126-132.

Zhang Jing, Chen Bingkui, Kang Chuanzhang, et al. Dynamic Analysis for Spur Gears Considering Friction Effect[J]. Journal of Vibration and Shock, 2012,31(21):126-132.

[17]李媛,刘小君,张彦.面接触条件下织构表面摩擦特性研究[J]. 机械工程学报, 2012, 48(19):109-115.

Li Yuan, Liu Xiaojun, Zhang Yan,et al. Frictional Properties of Textured Surfaces under Plane Contact[J]. Journal of Mechanical Engineering, 2012, 48(19):109-115.

[18]Ji Cuicui, Zhu Hua, Jiang Wei, et al. Running-in Test and Fractal Methodology for Worn Surface Topography Characterization[J].Chinese Journal of Mechanical Engineering, 2010, 23(5): 600-605.

[19]李兵, 刘焜, 王静, 等.线接触滑-滚条件下微凹坑表面摩擦特性研究[J].机械工程学报, 2011, 47(21):91-96.

Li Bing，Liu Kun，Wang Jing，et al. Micro Cavity’s Tribological Property under Line Contact and Sliding-rolling Conditions[J].Journal of Mechanical Engineering, 2011, 47(21): 91-96.

[20]尹延国,邢大淼,尤涛,等. 基于有限元法的面接触摩擦热流分配系数反推研究[J]. 摩擦学学报, 2012, 32(6): 592-598.

Yin Yanguo,Xing Damiao,You Tao,et al. Inverse Research on Partition Coefficient of Heat Flow under the Condition of Surface Contact Friction Based on the Finite Element Method[J]. Tribology, 2012, 32(6):592-598.

[21]王敏,杨兰玉.机床导轨爬行现象的研究[J].煤矿机械, 2004, 35(3): 35-37.

Wang Min, Yang Lanyu. The Study to Research Machine Tool Guideway Crawl Appearance[J].Journal of Coal Mine Machinery, 2004, 35(3): 35-37.

[22]杨勇, 王时龙,田志峰，等.大型数控滚齿机立柱动力学仿真分析[J]. 2013, 24(11): 1473-1479.

Yang Yong, Wang Shilong, Tian Zhifeng, et al. Dynamics Simulation Analysis of Column for Large-scale NC Gear Hobbing Machine[J]. China Mechanical Engineering, 2013, 24(11): 1473-1479.

[23]Vrande B L V D, Campen D H V, Kraker A D.An Approximate Analysis of Dry-friction-induced Stick[J].Nonlinear Dynamics, 1999,19(2):159-171.

[24]温诗铸, 黄平.摩擦学原理[M].北京:清华大学出版社, 2008.

[25]葛中民, 侯虞铿, 温诗铸.耐磨损设计[M].北京:机械工业出版社, 1991.

(编辑陈勇)

Abrasion Properties of Composite Sliding Guideways for Gear Hobbing Machines

Li XianguangYang Yong

Chongqing Machine Tool(Group)Co.,Ltd.,Chongqing，401336

In order to master the abrasion properties of composite sliding guideways of gear hobbing machines, based on the principle of crawl of vibration theory, Reynolds theory, and the working condition parameter of composite sliding guideway, a model of the stable attrition phase was established to calculate the attrition depth of changing with time, the experimental project for test the attrition depth of composite sliding guideway of the gear hobbing machine was proposed, and the corresponding experimental apparatus were developed successfully. The attrition depth were tested with the sample parts of composite sliding guideway of gear hobbing machine, the theoretical calculations were compared with the experimental values.It is shown that the relative error of the results is lower than 5%. The above analyses indicate the effectiveness and validity of the proposed method, which has beneficial reference value and instructive significance for optimum oil groove structure, geometry parameter, and oil film load-bearing capacity design, and type selection of composite sliding guideways on gear hobbing machines.

gear hobbing machine；composite；sliding guideway；abrasion ratio；attrition depth

TH117.1

10.3969/j.issn.1004-132X.2016.09.007

2015-06-17

重庆市百名工程技术高端人才培养计划资助项目；重庆市新产品创新青年科技人才培养计划项目(cstc2013kjrc-qnrc70001)；重庆市科技创新领军人才培养计划资助项目；重庆市杰出青年科学基金资助项目(cstc2014jcyjjq70001)

李先广，男，1966年生。重庆机床(集团)有限责任公司教授级高级工程师、博士研究生导师，数控制齿机床重庆市重点实验室主任，重庆大学客座教授。研究方向为数控齿轮加工机床动力学，齿轮加工技术及装备的绿色化与智能化。杨勇，男，1980年生。重庆机床(集团)有限责任公司高级工程师、博士。