5-UPS/PRPU冗余驱动并联机床弹性动力学分析

周　鑫　许允斗　姚建涛　郑魁敬　赵永生

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004



5-UPS/PRPU冗余驱动并联机床弹性动力学分析

周鑫1,2许允斗1,2姚建涛1,2郑魁敬1,2赵永生1,2

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

结合有限元法和子结构法建立了5-UPS/PRPU冗余驱动并联机床的弹性动力学模型。首先，将系统划分为不同的子结构，根据空间柔性梁理论求出单元动力学方程，根据关节特点将各个梁单元组装成各个驱动分支；根据分支与动平台的运动学/动力学约束，将各个分支进行装配，从而得到系统动力学方程。以5-UPS/PRPU冗余驱动并联机床作为算例，求出其动平台中心的动态响应特性。通过比较5-UPS/PRPU冗余驱动并联机床及5-UPS/PRPU非冗余驱动并联机床动平台的动态响应，可以得到结论：冗余驱动可以明显改善该机床弹性动力学特性，从而减小因弹性变形引起的误差。研究结果为结构设计人员进行结构设计及优化提供可靠的依据。

并联机床；冗余驱动； 弹性动力学；动态特性比较

0　引言

并联机器人具有刚度高、承载能力强以及模块化程度高[1-3]等特点，广泛应用于航空航天、国防军事等领域。然而，由于并联机器人的工作空间小、容易产生奇异位型等缺点，在实际生产中往往通过引入冗余驱动的概念去解决这些问题。

高速、轻型化是并联机器人发展的主要趋势。然而，当轻型化的机器人在重载且高速的环境下工作时，往往会由于各个分支的弹性变形影响其运动及动力学性能，从而降低机器人的精度。因此,有必要对并联机器人进行弹性动力学分析，并通过结构优化提高其动力学特性。Liu等[4]通过考虑连杆的变形，分析了3-RRS并联机构的动力学特性。胡俊峰等[5]提出了一种简单而精确的弹性动力学建模方法，并通过实例进行了验证。文献[6-9]分别针对不同的机构建立了弹性动力学模型，并且进行了相应的动力学分析。陈修龙等[10]基于机构的弹性动力学模型提出了一种优化方法。Cammarata等[11]提出了一种约束优化方法，该方法改善了3T1R并联机器人的弹性动力学性能；Alberto等[12]采用一种新的重力补偿方法，分析了四杆机构的弹性动力学特性；Zhang等[13]以3-PRS为例，通过建立其弹性动力学模型提出了一种能够分析其关节约束反力的方法。文献[14-16]分别从结构、理论方法以及控制的角度对3-PRR 柔性并联机器人进行了深入的分析。综上所述，现有文献大多针对非冗余驱动并联机构进行弹性动力学分析，而对于冗余驱动并联机构的分析并不多。Zhao等[17]比较了6-PSS与8-PSS冗余驱动并联平台的弹性动力学特性。除此之外，鲜有文献对冗余驱动并联机构的弹性动力学进行研究，对于通过将主动副代替被动副从而实现驱动冗余机构的相关研究更是鲜有报道。

本文对5-UPS/PRPU冗余驱动并联机构的弹性动力学性能进行了分析。首先通过结合子结构法和有限单元法，建立了空间单元的弹性动力学模型；然后根据各个关节的运动特性，将单元动力学模型进行组装，并根据机构的运动学/动力学约束，得到系统总体的弹性动力学模型；最后以相应的5-UPS/PRPU冗余驱动并联机床为算例，通过与相应的5-UPS/PRPU非冗余驱动并联机床动平台中心的弹性位移进行比较，证明冗余驱动对机床性能的改善。

1　动力学建模

5-UPS/PRPU五自由度冗余驱动并联机床如图1所示，它由定平台、动平台以及6条驱动分支等组成。机床的加工运动可以通过5条结构相同的UPS驱动分支及PRPU分支(冗余分支)的移动副共同实现。各个移动副的运动主要通过滚珠丝杠/螺母实现。此外，沿动平台中心的法线方向的转动被PRPU分支所约束，因此，PRPU分支也可以称为约束分支。R、U、S、P分别代表转动副、虎克铰、球副以及移动副。由于机床动平台能够实现运动的自由度数目是5，而驱动数目为6，故机床表示为5-UPS/PRPU五自由度冗余驱动并联机床。

图1　5-UPS/PRPU机床模型结构图

机床结构简图如图2所示。对于该冗余驱动五自由度并联机床，由于机床动平台以及定平台刚度很大，故忽略其弹性变形，在此假设其为刚形体；由于滑块刚度很大，同样将其考虑成刚体，忽略其弹性变形。因此，在本文分析过程中考虑5个UPS驱动分支的弹性变形；另外，将PRPU分支的RPU分支部分视为弹性体。

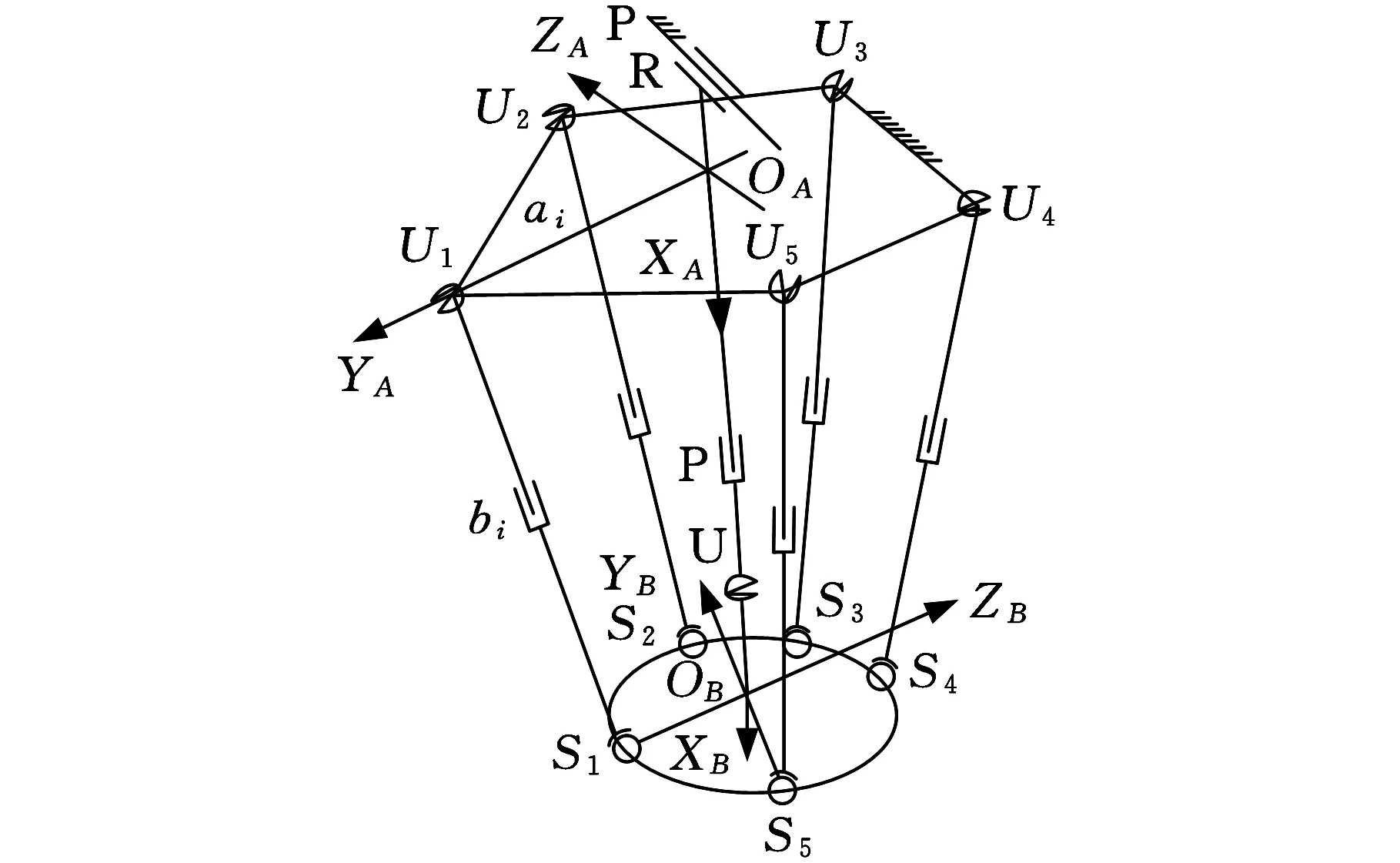
图2　5-UPS/PRPU机床结构简图

1.1单元动力学方程

根据机床分支实际结构，将空间柔性梁单元模型等效为圆柱形截面，如图3所示。该空间两单元两端坐标分别表示为δ1,δ2,δ3和δ10,δ11,δ12，δ4,δ5,δ6和δ13,δ14,δ15，δ7,δ8,δ9和δ16,δ17,δ18，即该梁单元的弹性位移、弹性转角以及曲率。单元E′处的弹性位移以及弹性转角可以表示为

(1)

式中，NT(x)为空间梁单元的位移形函数；δ为梁单元的广义坐标，δ=[δ1δ2…δ18]。

图3　空间柔性梁单元模型

将空间梁单元的动能表示为

(2)

式中，L、ρ、A、IP分别为梁单元的长度、密度、截面面积以及惯性矩。

将空间梁单元的势能表示为

(3)

式中，E、G、Iy、Iz分别为梁单元的拉压弹性模量、剪切弹性模量以及对y轴和z轴的主惯性矩。

将式(2)、式(3)分别代入以下拉格朗日方程：

(4)

可以得到空间梁单元的动力学方程：

(5)

其中，Me、Ke分别为单元质量矩阵及单元刚度矩阵；Fe表示单元所受外力，包括梁单元实际受到的载荷、与其他单元的相互作用力以及其惯性力。1.2分支及动平台的动力学方程[18]

首先分别将UPS分支以及PRPU分支等效为悬臂梁。对于PRPU分支，则将R0点考虑为固定端，故其弹性位移及转角均为0；对于P0点，由于该点(移动副)链接的两个单元分属不同的构件，故应当设置不同的弹性位移；对于U0处(虎克铰)可以等效成两个汇交不共面的转动副，所以，U0处对应的两个曲率也为0。对于UPS分支，同样将Ui(i=1,2,…,5)点考虑为悬臂梁的固定端，那么其弹性位移及转角均为零；由于Pi点连接两个不同的构件，故也设置不同的弹性位移；对应Si处为球铰，因此，沿三个方向的曲率也为零。各个分支的系统坐标系设置如图4所示。

对于PRPU分支，如果假设构件R0P0与坐标系R0xyz中的y轴夹角为θ01；对于各UPS分支，构件RiPi中的y、z轴夹角为θi2、θi3(i=1,2,…,5)，那么，PRPU分支的局部坐标系与参考坐标系AXYZ的旋转变换矩阵即可表示为

(6)

UPS分支的局部坐标系与参考坐标系AXYZ的旋转变换矩阵可以表示为

(7)

可以根据分支局部坐标系与参考坐标系的旋转变换矩阵将空间梁单元组装成支链，并且完成相应坐标系的转换。那么，机床各个分支的动力学方程可以表示为

(8)

U0=[u1u2…u22]T

Ui=[ui1ui2…ui21]Ti=1,2,…,5

(a)PRPU分支在参考坐标下的广义坐标

(b)UPS分支在参考坐标下的广义坐标图4　分支在参考坐标系下的广义坐标

其中，Mi、Ki、Fi分别为分支的质量矩阵、刚度矩阵以及分支所受的外载荷向量。U表示由各个分支在参考坐标系中的坐标所组成的向量。

1.3动平台动力学方程

根据前文的假设，由于动平台的刚度很大，故考虑成刚体，则动平台与各个驱动分支连接结点不是独立的。因此，假设动平台与各个驱动分支连接结点一致，且各驱动分支对动平台的力与作用在动平台的外力相平衡，由此可以分别得到系统的运动学约束方程及其动力学方程。

根据对动平台的动力学分析作为系统的动力学约束，有

(9)

1.4系统动力学方程的装配

将分支系统中的质量矩阵、刚度矩阵分解成以下形式：

通过将各个分支动力学方程(式(8))与动平台动力学方程(式(9))结合，再结合文献[19]中的运动约束方程即可得到5-UPS/PRPU冗余驱动并联机床整体弹性动力学方程：

(10)

U=[U0U1…U5u1u2…u6]T

C=λ1M+λ2K

M=

式中，M、C、K分别为系统的整体质量矩阵、阻尼矩阵以及刚度矩阵；F为系统所受到的外力的合力；λ1、λ2分别为系统的刚度阻尼及其质量阻尼的系数。

构造冗余驱动并联机构的方法有三种：①将被动运动副替换为主动运动副，即关节式的冗余驱动；②支链式的冗余驱动，即通过添加一条或多条驱动支链从而使机构的实际驱动链数目超过其运动所需的支链数目；③以上两种方法的综合。5-UPS/PRPU冗余驱动并联机床属于第一种类型，即通过添加冗余电机从而构造出冗余驱动。值得注意的是,冗余电机的添加，使得整个系统具有6个驱动输入。理论上而言，机床的任意位姿都对应着无穷多组解。因此，在确定各个分支的驱动力时，允许根据不同的优化目标通过采用不同的优化算法优化机床分支的驱动力。考虑到实际的加工问题，本文采用文献[20]中的优化方法，根据达朗伯原理求解冗余分支的驱动力，从而以使冗余分支的大滑块能够更好地跟随动平台运动为优化目标。另外，对于非冗余驱动并联机床的驱动力，则可根据拉格朗日方程直接求出。机床刚体动力学的部分不再赘述。

2　动态响应分析

2.1机床动态响应特性分析

为了分析系统的动态响应特性，令5-UPS/PRPU五自由度冗余驱动并联机床的动平台中心的运动轨迹为

(11)

(12)

可以根据式(10)求出系统的动态响应特性。机床的基本尺寸及结构参数见表1～表3。

表1　机床基本结构参数

表2　UPS 分支基本结构参数

表3　PRPU 分支基本结构参数

动平台的质量为45 kg, 密度为 7800 kg/m3, 剪切弹性模量为79 GPa, 拉压弹性模量为210 GPa。

为了比较机床在冗余驱动与非冗余驱动的动态响应特性，分别计算了5-UPS/PRPU冗余驱动并联机床与其相应的5-UPS/PRPU非冗余驱动并联机床动平台中心的弹性位移以及对应的刚性位移。如图5～图10所示，实线部分表示冗余驱动并联机床动平台中心的弹性位移，虚线部分表示非冗余驱动并联机床动平台中心的弹性位移。

图5　沿x轴方向的线位移

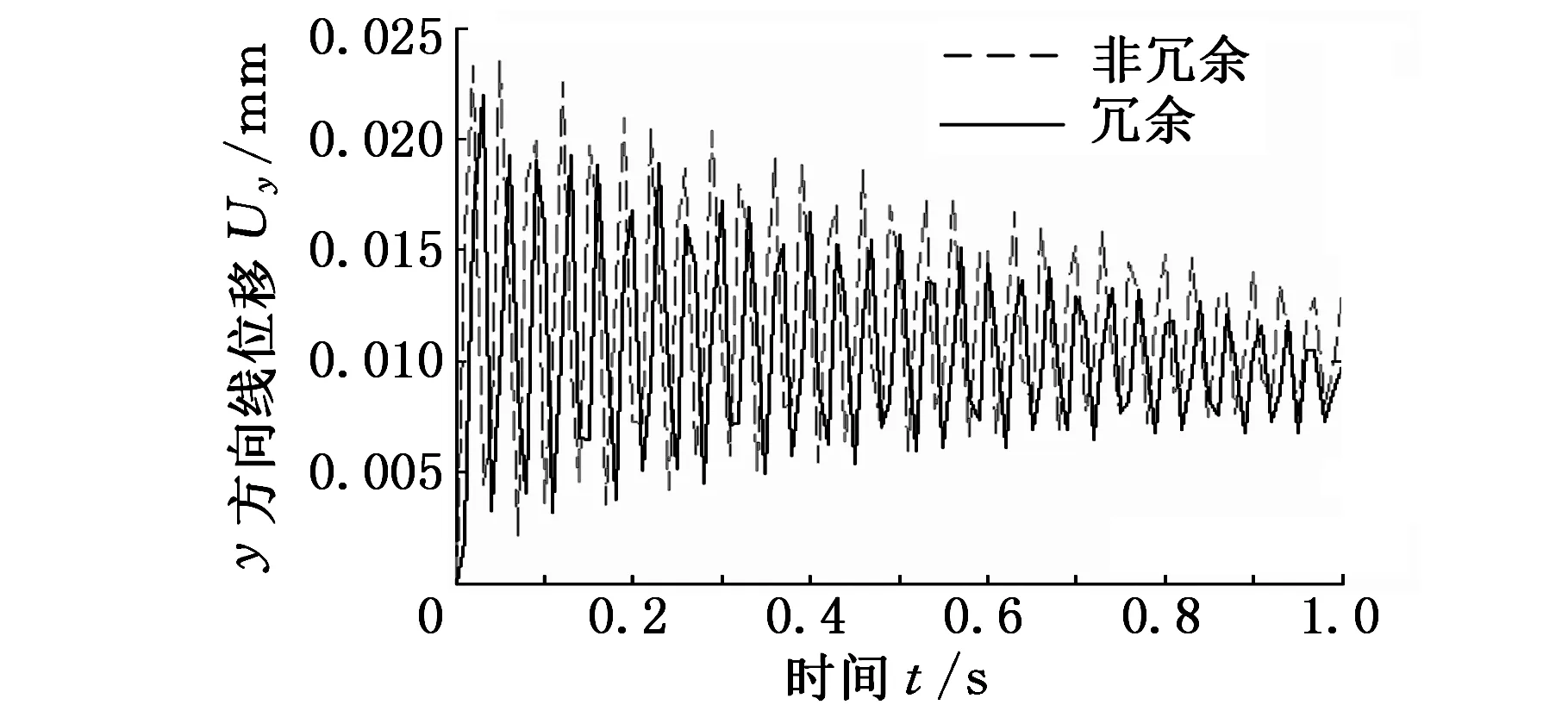
图6　沿y轴方向的线位移

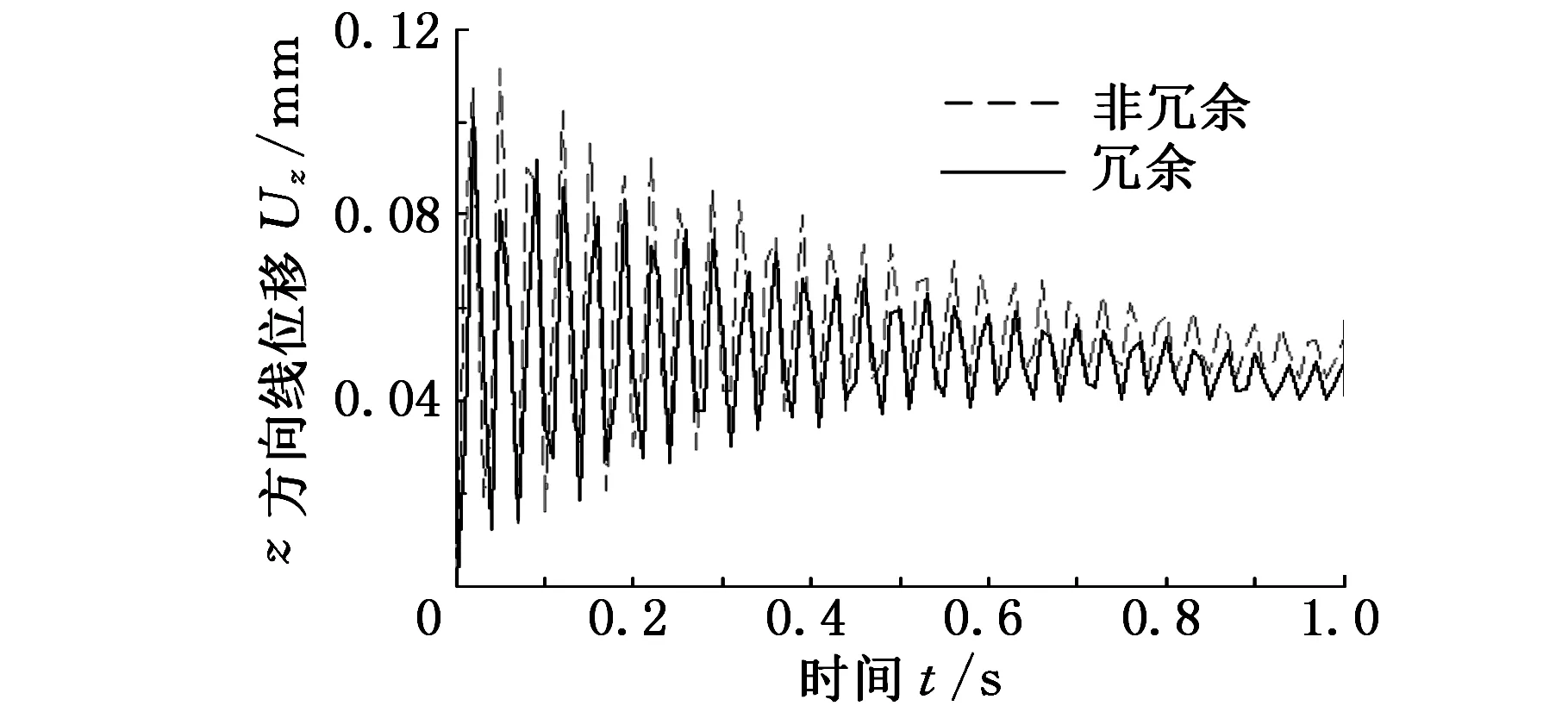
图7　沿z轴方向的线位移

图8　沿x轴方向的角位移

图9　沿y轴方向的角位移

图10　沿z轴方向的角位移

比较分析图5～图10可知冗余驱动对机床整体动态响应的影响情况。对于冗余驱动并联机床，由分支变形引起平台中心在x、y、z方向的线/角位移的最大误差值分别为-0.0189 mm、0.0219 mm、0.1008 mm; -0.1507°、 0.1361°、0.0064°。而对于非冗余驱动并联机床，各个方向的最大误差值分别为-0.021 mm、0.0236 mm、0.1114 mm；-0.1581°、0.1403°、0.0068°。由此可见，无论是对于冗余驱动还是非冗余驱动并联机床，最大移动误差均沿z方向，转动方向的最大误差值均沿x方向。除此之外，可以看出该冗余驱动并联机床在x、y、z三个方向的移动误差及x、y方向的转动误差均小于其非冗余驱动并联机床，且最大移动误差减小了0.0106 mm, 最大转动误差减小了0.042°。因而可以得出冗余驱动可以改善机床的动态响应特性的结论。

需要说明的是，由于各个方向的实际位移均以某一数值为中心往复波动，说明其动平台中心点由于各个驱动分支变形所引起的弹性位移是以某一点为中心的弹性振动。

2.2仿真验证

该冗余驱动并联机床的固有频率由下式得到：

det(-ω2M+K)=0

(13)

图11　冗余驱动并联机床各阶固有频率仿真结果

通过观察式(13)不难发现，该机床的整体质量矩阵和刚度矩阵均与机床的位姿相关，因此，计算了机床在不同位姿下的固有频率，并通过有限元软件中的模态分析进行验证。图11所示为机床在初始位姿时各阶固有频率在有限元仿真软件中的计算结果，比较分析可知，本文理论模型所得结果与有限元仿真结果的变化趋势一致，可以在一定程度上证明本文模型的有效性。

3　结论

(1)本文结合有限单元法与子结构法推导了5-UPS/PRPU冗余驱动并联机床的弹性动力学模型。

(2)比较了5-UPS/PRPU冗余驱动并联机床与其非冗余驱动并联机床的动态响应特性。

(3)冗余驱动可以在一定程度上改善冗余驱动并联机床的动态响应特性。此外，可以采用本文的方法对系统结构进行优化；通过理论分析找到机床误差最小的位置，从而进行轨迹规划，提高机床加工精度。

[1]马立，谢炜，刘波，等. 柔性铰链微定位平台的设计[J]. 光学精密工程, 2014,22(2):338-345.

MaLi,XieWei,LiuBo，etal.DesignofMicro-positionStagewithFlexureHinge[J].OpticsandPrecisionEngineering,2014, 22(2):338-345.

[2]吕帮俊，朱石坚，彭利坤，等.Stewart机构刚度映射建模与仿真[J]. 振动与冲击，2011，30(4)：178-181.

LüBangjun,ZhuShijian,PengLikun,etal.StiffnessMappingModelingandSimulationforStewartMechanism[J].JournalofVibrationandShock，2011，30(4)：178-181.

[3]RizkR,MunteanuM,FaurouxJC,etal.AComparativeStiffnessAnalysisofaReconfigurableParallelMachinewithThreeorFourDegreesofMobility[J].JournalofMachineEngineering，2006，6(2)：45-55.

[4]LiuShanzeng,YuYueqing,ZhuZhencai,etal.DynamicModelingandAnalysisof3-RRSParallelManipulatorwithFlexibleLinks[J].JournalofCentralSouthUniversity, 2010, 17:323-331.

[5]胡俊峰，张宪民，朱大昌，等.柔性并联机器人动力学建模[J].农业机械学报，2011，42(11):197-202.

HuJunfeng,ZhangXianmin,ZhuDachang,etal.DynamicModelingofFlexibleParallelRobot[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2011, 42(11):208-213.

[6]杜兆才，余跃庆，张旭平，等.平面柔性并联机器人动力学建模[J].机械工程学报，2007，43(9): 96-101.

DuZhaocai,YuYueqing,ZhangXuping,etal.DynamicModelingofPlanarFlexibleParallelManipulators[J].ChineseJournalofMechanicalEngineering,2007，43(9):96-101.

[7]韩亚锋，马履中，吴伟光，等.Delta并联机器人弹性动力学研究[J].农业机械学报，2011，42(10):197-202.

HanYafeng,MaLüzhong,WuWeiguang,etal.ElasticDynamicAnalysisofDeltaParallelRobot[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2011, 42(10):197-202.

[8]张清华, 张宪民. 平面3-RRR和3-PRR柔性并联机器人弹性动力学分析[J]. 华南理工大学学报(自然科学版), 2012, 40(11):52-57.

ZhangQinghua,ZhangXanmin.ElastodynamicAnalysisofPlanar3-RRRand3-PRRFlexibleParallelRobots[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2012, 40(11) :52-57.

[9]张清华, 张宪民.平面3-RRR柔性并联机器人动力学建模与分析[J].振动工程学报, 2013, 26(2):239-245.

ZhangQinghua,ZhangXanmin.DynamicModelingandAnalysisofPlanar3-RRRFlexibleParallelRobots[J].JournalofVibrationEngineering,2013,26(2): 239-245.

[10]陈修龙, 张中供, 邓昱.空间并联机构弹性动力学优化设计[J].农业机械学报, 2014, 45(9): 318-323.

ChenXiulong,ZhangZhonggong,DengYu.Elasto-dynamicsOptimalDesignofSpatialParallelMechanism[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2014, 45(9): 318-323.

[11]CammarataA,SinatraR.ElastodynamicOptimizationofa3T1RParallelManipulator[J].MechanmismandMachineTheory, 2014,73:184-196.

[12]AlbertoM,MarcoT,MarcoC,etal.ElastodynamicBehaviorofBalancedClose-loopMechanisms:NumercalAnalysisofaFour-barLinkage[J].Meccanica, 2014,49(3):601-614.

[13]ZhangJun,ZhaoYanqin.ElastodynamicModelingandJointReactionPredictionfor3-PRSPKM[J].JournalofCentralSouthUniversity, 2015, 22(8):2971-2979.

[14]PirasG,CleghornWL,MillsJK.DynamicFiniteElementAnalysisofaPlanarHigh-speed,Hign-precisionParallelManipulatorwithFlexibleLinks[J].MechanismandMachineTheory, 2005, 40(7): 849-862.

[15]WangXiaoyun,MillsJK.DynamicModelingofaFlexible-linkPlanarParallelPlatformUsingaSubstructuringApproach[J].MechanismandMachineTheory, 2006,41(6):671-687.

[16]Wang Xiaoyun, Mills J K. A FEM Model for Active Vibration Control of Flexible Linkages[C]//Proceding of IEEE International Conference on Robotics and Automation.Piscataway, 2004: 4308-4313.

[17]Zhao Yongjie, Gao Feng, Dong Xingjian,et al.Elastodynamic Characteristics Comparison of the 8-PSS Redundant Parallel Manipulator and Its Non-redundant Counterpart-the 6-PSS Parallel Manipulator[J].Mechanism and Machine Theory, 2010,45(2):291-303.

[18]Wang Dan, Fan Rui, Chen Wuyi. Stiffness Analysis of a Hexaglide Parallel Loading Mechanism[J].Mechanism and Machine Theory, 2013, 70(6): 454-473.

[19]刘善增.三自由度柔性并联机器人动力学研究[D].北京：北京工业大学，2009.

[20]程丽.五自由度并联机床冗余驱动理论与实验研究[D].秦皇岛：燕山大学，2009.

(编辑陈勇)

Elastodynamics Analysis of a 5-UPS/PRPU Redundantly Actuated Parallel Machine Tool

Zhou Xin1,2Xu Yundou1,2Yao Jiantao1,2Zheng Kuijing1,2Zhao Yongsheng1,2

1.Parallel Robot and Mechatronic System Laboratory of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of National Education,Yanshan University,Qinhuangdao,Hebei,066004

An elastodynamics model of the 5-UPS/PRPU redundantly actuated PMT was derived by combining the finite element model and substructure synthesis techniques herein. Firstly, the overall system was divided into different substructures. According to the theory of spatial beam element, the dynamics equation of the spatial beam element was derived, and then assembling into different driving limbs; according to the dynamic constraints and kinematic constraints among the moving platform and each driving limbs, the dynamics equation of the overall system might be obtained by assembling the dynamics equation of the driving limbs. The 5-UPS/PRPU redundantly actuated PMT was set as an example to illustrate the derivation of the dynamic response of the moving platform. At last, by comparing the dynamic response of the redundantly actuated PMT and its non-redundant PMT, it can be concluded that: the elastodynamics performance of the PMT may be improved by the actuation redundancy, so that the errors caused by the driving limb deformations can be reduced as well. The research provides a theoretical reference of the structure design and optimization for the designers.

parallel machine tool(PMT); actuation redundancy; elastodynamics; dynamic performance comparison

2015-11-06

国家自然科学基金资助项目(51275439)；燕山大学青年教师自主研究计划资助项目(13LGA001)

TP394.1；TH691.9

10.3969/j.issn.1004-132X.2016.09.001

周鑫,男,1988年生。燕山大学机械工程学院博士研究生。主要研究方向为并联机器人理论及其应用。许允斗,男,1985年生。燕山大学机械工程学院讲师。姚建涛,男,1980年生。燕山大学机械工程学院副教授。郑魁敬,男,1971年生。燕山大学机械工程学院副教授。赵永生(通信作者),男,1962年生。燕山大学机械工程学院教授、博士研究生导师。