三臂式巡检机器人重力平衡及其转向越障方法
2016-09-05陶广宏房立金
陶广宏 房立金
东北大学,沈阳,110819
三臂式巡检机器人重力平衡及其转向越障方法
陶广宏房立金
东北大学,沈阳,110819
提出了一种由4组平行四边形机构串联组成的新型三臂式巡检机器人机构,该机构能够通过调节机器人的姿态来满足越障过程中的重力平衡要求。给出了机器人越障流程规划,并对转向越障中的关键步骤进行了分析,利用二分逼近优化算法搜寻满足重力平衡条件的越障姿态,给出了满足重力平衡约束条件的运动学逆解求取方法,实现了机器人重力平衡约束条件下的转向越障运动。分析结果表明,该新型三臂式巡检机器人具有转向跨越障碍的能力。
重力平衡;转向;越障;巡检机器人
0 引言
近年来,国内外学者针对电力输电线路巡检机器人开展了大量研究,提出了多种形式的机器人结构,部分机器人已经在电力部门得到了实际应用。但由于机器人的重力平衡问题,现有的机器人大多是在直线线路上使用,在转角塔处跨越障碍和转向行走方面还存在很多不足。
现有的输电线巡检机器人可分为双臂结构、多臂结构和三臂结构三大类。双臂结构是现阶段最具代表性的结构形式,由于其越障有单臂挂线行进的过程,会出现侧摆等不稳定状态[1]。典型的有日本HiBot公司研制的Expliner[2],它具有8轮双臂的结构,通过调整机器人下方的杆式机构来保证机器人的重力平衡。中国科学院沈阳自动化所[1-3]和武汉大学[4]等研究机构也分别设计出双臂回转式的巡检机器人样机。加拿大魁北克水电研究院推出了名为Linescout的巡检机器人样机[5-6],采用两对手臂交互的越障方式,其中每对手臂为同一构件,可视为同一手臂,因此,该结构实为双手臂结构形式,始终保持其中一对手臂挂线,安全系数高,但该机构没有水平旋转副,不具备转向越障的能力,因此,不存在侧向重力平衡问题。
多臂结构均具有转向越障能力且工作稳定性强,不存在单臂挂线过程,因此,纵向实时处于重力平衡状态且可通过调整机器人姿态保证其侧向重力平衡,但存在驱动电机过多、机构总体尺寸大、能耗大、控制困难等缺点。典型的有Aoshima等[7]于1989年提出的六臂结构,该机器人由6个具有升降臂和行走轮的单元串联组成,其两手臂间距固定,越障能力受限。房立金等[8]也提出了一种五手臂结构,该机构由4个单元机构串联组成,能够实现越障过程的侧向重力平衡,具有多种越障模式,但其结构复杂。
三臂结构工作过程稳定,同时结构和控制方式相对简单。山东科技大学[9]、西安交通大学[10]、湖南大学[11]等分别设计出三臂式的巡检机器人原型机,都通过3支手臂的交替脱线挂线来适应无水平转角的障碍环境。虽然现有三臂结构在中间手臂挂线时,前侧或后侧手臂可以通过另一手臂的下线来实现重力纵向及侧向平衡,但转向越障时中间手臂的脱线挂线过程会由于前后手臂均处于挂线状态、无侧向平衡重力矩而导致机器人的侧向倾斜,难以准确定位机器人姿态来完成越障任务。由于在实际应用中转角塔是不可避免的障碍环境,故具有转向越障能力的三臂式巡检机器人机构在技术上及经济实用方面均具有广阔的发展前景。
本文通过对巡检机器人在架空地线上跨越转角塔等具有水平转角障碍时存在重力平衡问题分析,提出了一种由4个平行四边形机构串联组成的三臂式巡检机器人机构,并给出转向越障流程及实现算法。
1 巡检机器人转向越障重力平衡问题
输电线路巡检机器人的重力平衡问题可分为纵向重力平衡问题和侧向重力平衡两大类。
1.1纵向重力平衡问题
纵向重力平衡是在只有单一手臂抓线时才可能出现的机器人在行进方向的前后倾斜现象。该问题主要存在于双臂式巡检机器人单臂挂线越障过程。现有的三臂式巡检机器人在跨越直线障碍时,由于至少有2个手臂挂线,故不会出现前后倾斜现象。转向越障或进行其他操作时,为保证机器人的侧向不倾斜,需要其后侧或前侧手臂下线而仅剩中间手臂抓线,此时也可能会出现由于纵向重力不平衡而导致的机器人前后倾斜现象。该问题是由于机器人质心未实时处于挂线手臂上,而导致机器人本体相对于挂线手臂产生的重力矩前后不相等而造成的。本文所提出的三臂式巡检机器人在越障时至少有2个手臂抓线,从机构设计及越障机理上解决了巡检机器人的纵向重力平衡问题。
1.2侧向重力平衡问题
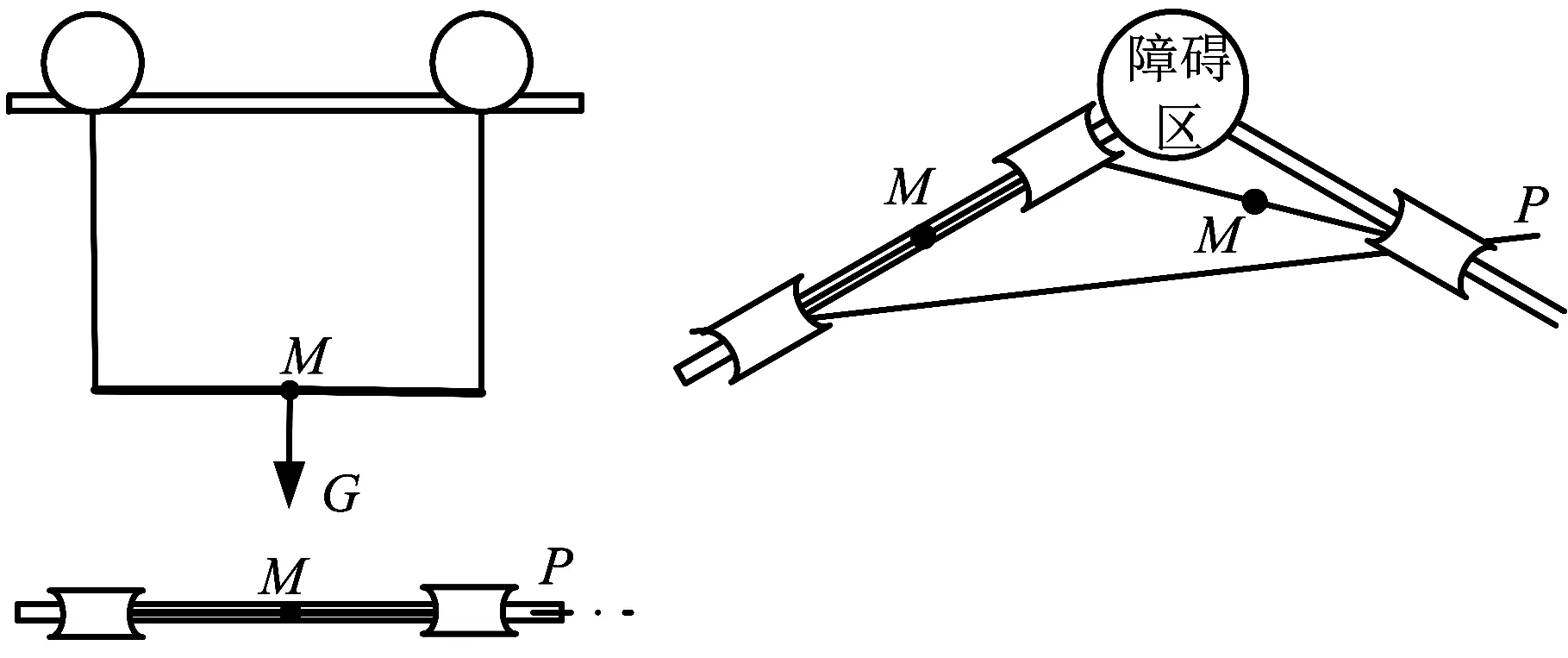
(a)主视及俯视图(b)转向越障俯视图图1 已有三臂机器人相邻手臂间机构及其转向示意图
三臂式巡检机器人越障的难点在于转向越障时,如何将机器人的质心调整到期望的竖直平面上,以保证机器人的侧向重力平衡,从而精确地定位机器人手臂进行抓线运动。已有的三臂式巡检机器人两手臂间的结构可归结为机构的质心位于两手臂间且无法相对于两手臂所在的竖直平面P进行侧向相对运动,因此,机器人的质心调节能力受限,只有在单一中间手臂支撑时才可以满足侧向重力平衡要求(图1a)。当遇到图1b所示需要前后两手臂支撑、中间手臂抬升跨越转角障碍的情况时,机器人的质心M位于图中竖直平面P的同一侧,导致中间手臂行走轮无法抬升以跨越障碍。因此,已有的三臂式巡检机器人机构从原理上便不具备跨越转角塔等具有水平转角障碍环境的能力。
本文提出了一种两单元串联机器人机构。每个单元机构包括2个平行四边形机构,由水平旋转关节串联组成,如图2所示。在两手臂固定且距离小于2个平行四边形长度之和时,中间的两平行四边形机构具备侧向偏出并同时绕O1O2旋转的运动能力。根据结构特点,若取单元机构的质心分别位于两平行四边形机构中心及2个平行四边形机构间的连接处(图2a中A、M、B点),则机器人单元机构的质心A、M、B相对于两行走轮连线所在竖直平面P所成重力矩力臂,即各质心与两行走轮连线所在竖直平面的水平面投影距离dA、dM、dB取值有如下关系(当2个单元机构串联时,质心位于期望机器人整体质心所在竖直平面同一侧的dA、dM、dB同号,异侧则取其相反数):
(1)
式(1)说明,本机器人单元机构具有质心自我调节能力,因此,该形式的2个单元机构串联所组成的三臂式机构可以通过调整各单元机构中dA、dM、dB的取值来实时调整机器人整体的质心位置,满足转向越障重力平衡要求,如图2b所示。

(a)单元机构三视图

(b)整机转向越障俯视图图2 本文提出的机器人机构运动示意图

(a)机器人模型

1.输电线路 2.夹持机构 3.行走轮 4.驱动柔索 5.平行四边形机构铰接关节 6.复合旋转副 7.平行四边形机构 8.单元内水平旋转关节 9.手臂机构 10.两侧手臂旋转关节(b)机器人结构简图图3 机器人结构简图及实体模型
2 新型三臂式机器人结构
如图3所示,以相邻两手臂间的2个串联平行四边形机构为一个单元,则该机构由2个单元机构所组成。单元机构前后有手臂9和安装在手臂上端、由行走轮3和夹持机构2构成的轮爪复合机构,单元机构间用复合旋转副6连接,复合旋转副6为行星轮式结构,由2个电机配合驱动,保证前后平行四边形机构及手臂能够独立自由转动。每个单元机构还包括2个平行四边形机构7,单元机构内的平行四边形机构用水平旋转副8连接。位于机器人最前端和最后侧2个手臂与相邻的平行四边形机构用水平旋转副10连接。平行四边形机构的杆件采用关节5铰接,采用两条柔索4分别连接平行四边形机构的2个顶点,通过电机驱动安装在四边形机构上的滚筒来控制机构对角线的长度,从而控制机构的俯仰运动。
该机器人手臂结构简单,自身无需上下伸缩机能,通过单元机构中两串联平行四边形机构的俯仰运动实现手臂的上升下降运动,单元机构工作空间能够满足轮爪复合机构的上下线需求[8]。
3 新型三臂式巡检机器人转向越障流程及算法
3.1转向越障动作规划
本机构的直线越障方式与已有的三臂机器人[9-11]越障方式基本相同。
当机器人遇到转角障碍环境时,可采用实时保证机器人侧向重力平衡的伸缩越障模式,越障过程如图4所示。由输电线路的具体构造知转角处的障碍为下侧可通过式障碍,图中机器人机构与障碍区重叠部分表示可能位于输电线路下侧的部分机器人机构。点划线P表示机器人质心所在的竖直平面。不规则三角形区域表示机器人质心所在区域。

图4 转向越障流程俯视图
根据质心的调整过程,可将该机器人的转向越障分为五个阶段:
阶段1机器人的质心位于输电线路1所在竖直平面阶段。共有以下4步:
(1)当检测到转角障碍环境时,机器人调整到图4中(1-1)所示的收缩模式,此时机器人的平行四边形机构侧向偏出较少。
(2)行走轮1下线,该过程与行走轮2配合的夹持机构夹紧输电线路,与行走轮3配合的夹持机构松开,调整轮2-轮3运动链的姿态以保证机器人侧向重力平衡, 如图4中(1-2)所示。
(3)轮2夹持机构松开,在线行走轮2、3行进,使轮2靠近障碍区域,如图4中(1-3)所示。
(4)轮2夹持机构夹紧输电线路,调整轮1的位置及轮2-轮3运动链的姿态,使轮1落在输电线路2上,如图4中(1-4)所示。
阶段2机器人的质心由输电线路1所在竖直平面向行走轮1与行走轮3连线所在竖直平面的过渡阶段。共1步:
在3个行走轮同时落线时,如图4中(2-1)所示,轮2夹持机构夹紧输电线路,分别调整轮2-轮3运动链及轮2-轮1运动链的姿态。为增加轮2在输电线路2上的可夹持区域,使轮1运动到距离转角障碍较远的位置。该过程中3个行走轮均位于输电线路上,因此,只需保证机器人质心位于图4中(2-2)、(2-3)灰色区域的竖直空间内即可保证机器人质心稳定过渡到图4中(2-4)所示的轮1与轮3连线所在竖直平面P上。
阶段3中间手臂越障阶段,即行走轮2由输电线路1运动到输电线路2上。共有以下两步:
(1)在机器人质心过渡到行走轮1与行走轮3连线所在竖直平面后,行走轮1与行走轮3夹持机构分别夹紧输电线路,如图4中(3-1)所示。
(2)行走轮2脱线并沿能够保证机器人存在平衡位姿运动学逆解且与障碍无干涉的预定轨迹运动到输电线路2上并抓线,如图4中(3-2)、(3-3)所示。该步骤需实时调整机器人轮3-轮1运动链的姿态,保证机器人的质心始终位于轮1与轮3连线所在的竖直平面内,使机器人不发生影响行走轮抓线定位的侧倾现象。
阶段4机器人质心由行走轮1与行走轮3连线所在竖直平面向输电线路2所在竖直平面的过渡阶段。该阶段与阶段2类似。
阶段5机器人质心位于输电线路2所在竖直平面阶段。该阶段与阶段1类似。
通过以上5个阶段的连续进行即可完成转向越障。由以上流程可知,机器人在越障过程中不存在单臂挂线运动情况,通过侧向偏出的2个平行四边形机构实现侧向重力平衡,可以增加机器人越障过程的稳定性。
3.2转向越障算法设计
3.2.1侧向重力平衡条件
保证机器人转向越障侧向平衡的基本要求,即机器人质心位于期望的竖直平面上,条件可以表示为
(2)
其中,Mh为机器人各质点相对于期望平面的力矩之和;mi为机构第i个质点的质量;di为第i个质点到期望平面间的水平投影距离;g为重力加速度;为区别位于期望竖直平面两侧的质点所形成重力臂的正负取值,引入ti表示第i个质点所产生重力矩正负的因子。
在机器人实际应用时,两行走轮抓线会由于摩擦产生微小的对抗机器人侧倾的扭矩,因此,当机器人处于满足下式:
|Mh|≤ε
(3)
的姿态时,认为机器人质心处于期望的竖直平面内。本文利用二分逼近原理,当算法迭代至式(3)条件时,便认为该机器人姿态满足重力平衡要求。其中,ε为对抗机器人侧倾的摩擦力矩,同时可认为是二分逼近算法的允许误差界。
3.2.2机器人坐标系
平行四边形设计使机器人的3个手臂处于实时平行状态,在求解逆运动学时,保证基坐标的手臂处于竖直状态,机器人的末端机械手姿态便已确定,只求解其位置变量即可,简化求解过程,本文中基坐标所在手臂均为竖直状态。建立以轮3所在手臂为大地坐标的机器人D-H坐标系,如图5所示。

图5 机器人D-H坐标系
由机器人机构可知,图5中l2=l5=l8=l11, l1=l3=l4=l6=l7=l9=l10=l12=0,θ3=-θ2, θ6=-θ5, θ9=-θ8, θ12=-θ11。机器人转向越障问题即满足重力平衡约束的八自由度机器人运动学逆解问题。机器人在越障的过程中,机构本身存在运动学的多解。将8个自由变量的运动学逆解求解问题转化为分别求解轮2-轮1运动链和轮2-轮3运动链的四自由度机器人运动学逆解问题。通过综合设置对于单一运动链中两俯仰关节角度相等的方法和柱坐标变换方法(具体应用见3.3节)来简化未知变量,进行转向越障各阶段重力平衡约束下的机器人运动学逆解求解。
3.2.3柱坐标变换

(a)柱坐标变换示意图

(b)x21y21平面投影示意图图6 柱坐标变换
以阶段3初始姿态为例来说明柱坐标变换方法,如图6a所示。将原坐标系O2x2y2z2绕y2轴逆时针旋转β角,令变换后的坐标系O21x21y21z21的z21轴与输电线路1重合。
将A、M、B点写成柱坐标形式,分别为(ρA,γA,zA)、 (ρM,γM,zM)、(ρB,γB,zB), 已知图6a中O2M、EM为平行四边形机构的长度l2,A、B两点分别为O2M、EM中点。图6b中O21M1为O2M、EM在x21y21平面上的投影,由几何关系可知两杆件投影必在同一直线上。因此,ρA、ρB、ρM、zA、zB、zM可由几何关系直接各自求出且γA=γM=γB。令
γA=γM=γB=γ
由以上过程可得出各点在坐标系O21x21y21z21中以γ为未知变量的坐标表达式,令各点在坐标系O2x2y2z2中的笛卡儿坐标向量为r2,在坐标系O21x21y21z21中的笛卡儿坐标向量为r21,通过下式可将各点坐标由坐标系O21x21y21z21转化至坐标系O2x2y2z2中:
r2=Rβr21
(4)
通过以上变换,可分别求出A、M、B点在坐标系O2x2y2z2中的坐标,各坐标仅包含1个未知变量γ。由于柱坐标变换后影响力矩之和Mh的变量仅为γ且绕变换后的z轴旋转360°连续取值,因此,Mh的取值周期为2π,并在其同一周期内最大值与最小值区间内严格单调。
3.2.4质点力矩符号判断
假定已知所要确定期望平衡的竖直平面所在直线的两点为(x1,y1,z1)、(x2,y2,z2),则连接两点的直线方程可表示为
(5)
该直线在竖直方向平面P的方程为
Ax+By+D=0
(6)
D=-Ax1-By1
由点到平面距离公式可求得各质心与所求平面P的距离。根据本文机器人工况,令输电线路1位于大地坐标系XZ平面内,若质点位于该点在平面P上的垂足的一侧,则该点必然位于过该点平行于y轴方向的直线与该平面交点的同一侧。由该性质可推出质心位于平面P前侧还是后侧的判定条件。假定机器人上某质点的坐标(a,b,c),与y轴平行的向量为(0,1,0),根据点向式得到过该质点且与y轴平行的直线方程为

(7)
代入平面P的方程得到交点的y方向坐标:
(8)
符号因子可表示成
3.3典型阶段的算法流程设计
已知机器人转向越障运动过程中行走轮运动轨迹由若干给定工作空间内直线所组成,本算法的任务为采用将直线定步长等分的离散方式来确定每一离散点满足重力平衡条件的机器人各关节角度,以保证机器人越障过程中处于重力平衡状态。
由于越障过程中阶段5与阶段1类似,阶段4与阶段2类似,本文仅给出阶段1、2、3的转向越障算法流程。阶段1与阶段2的算法流程分别如图7、图8所示。阶段3算法流程如图9所示。图7~图9中出现的封装模块内容如图10所示。转向越障阶段2算法流程中H为
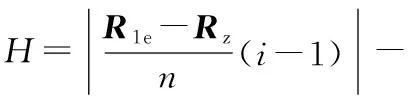
(9)
4 转向越障仿真分析
由转向越障各阶段流程算法可知越障阶段3算法复杂,且阶段3为机器人中间手臂越障阶段,是三臂式巡检机器人跨越转角障碍的关键,选取阶段3进行数值仿真分析。
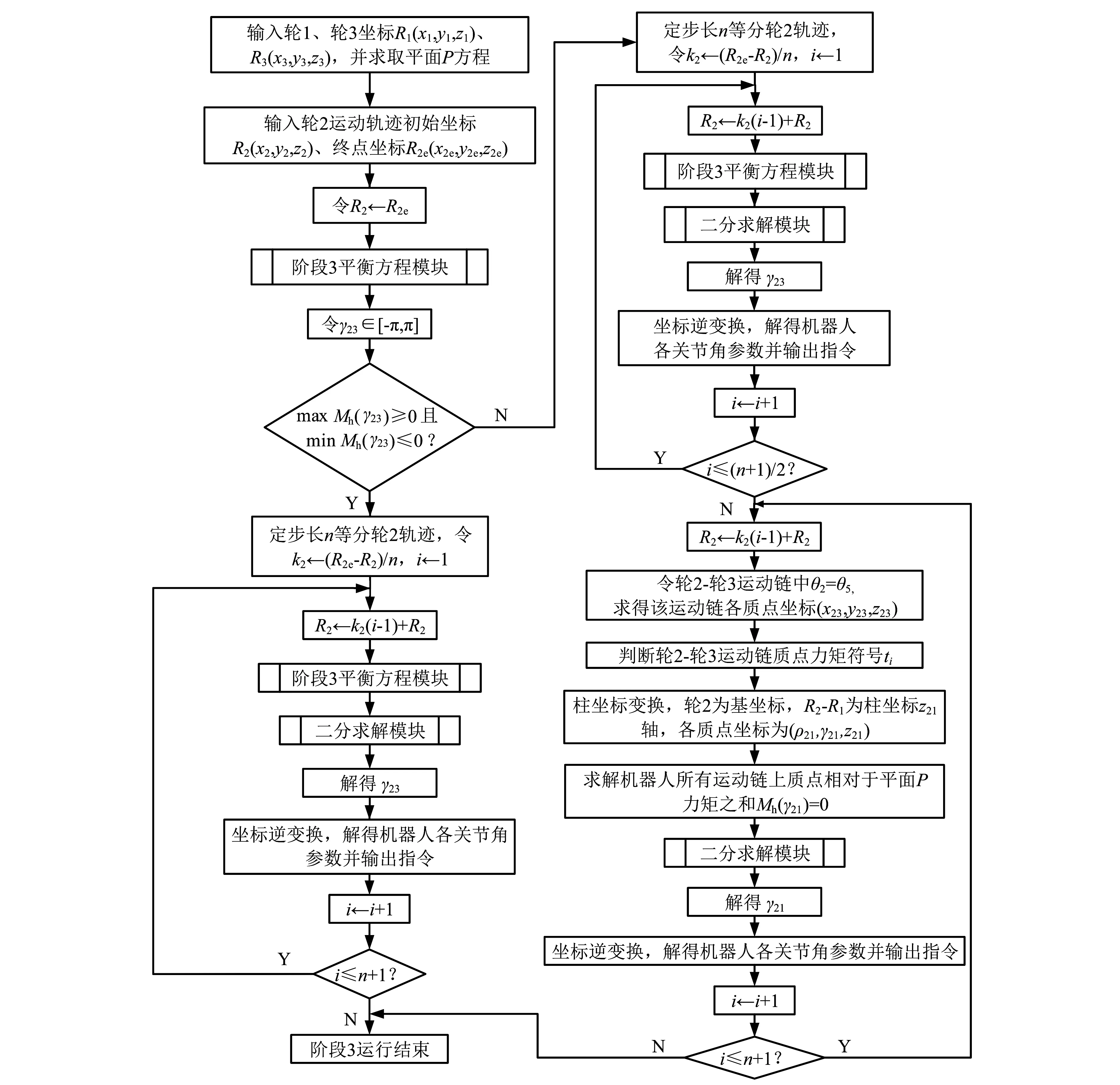
图9 阶段3算法流程
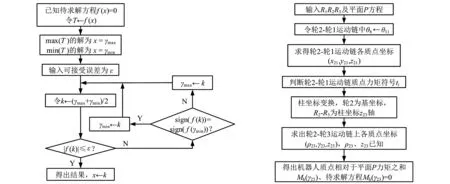
(a)二分求解模块(b)阶段3平衡方程模块图10 封装模块流程
以行走轮3所在位置为大地坐标系,行走轮2起点x方向坐标为0.25m,两输电线路交点J的x方向坐标为0.35m,行走轮2目标落线点与J点距离为0.15m, 行走轮1与J点距离为0.3m。两输电线路俯角均为15°,在水平投影夹角为120°,机器人质点简化为各杆件中点,机器人关节点,各质点质量为2kg。机器人平行四边形机构长为0.25m。令机器人摩擦侧倾对抗扭矩ε为0.001N·m,轮2的越障路径为距离最短路径,即起始点与目标点间的线段。在保证实时侧向重力平衡的条件下,令机器人匀速用18s完成越障过程。运动过程及相应参数取值如图11所示。

图11 中间手臂越障过程示意图
利用图9所示算法可求得行走轮2在输电线路2上落线,变量γ23取值区间为[-π,π],轮2与两输电线路交点距离s2取值区间为[0.1,0.2],轮1与输电线路交点距离为0.3m,在轮2-轮3运动链采用柱坐标变换方法得到的Mh值及等高线图分别如图12a、图12b所示。
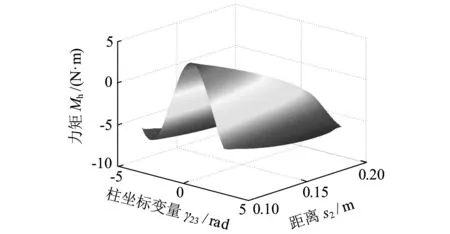
(a)力矩

1.Mh=-1 N·m 2.Mh=0 3.Mh=1 N·m(b)等高线图12 轮2输电线路2落线Mh值及等高线
由图12可以看出轮2在输电线路2上落线,与两输电线路交点的距离为0.15m时,采用在轮2-轮3运动链进行柱坐标变换的方式存在力矩Mh=0的姿态,即满足阶段3算法流程中的初始判别条件。继续进行阶段3算法流程,得到柱坐标变量γ23值,如图13所示。图14所示为机器人(θ1,θ2,θ4,θ5,θ7,θ8,θ10,θ11)关节角度的实时变化值,图15所示为机器人转向越障过程中Mh的变化情况。

图13 γ23变化过程

图14 关节角度变化过程

图15 Mh变化过程
由图14可以看出机器人各关节角度变化均在-2.5~2.5rad范围内,属于可接受的范围,且在运行阶段内各关节角度无突变。由图15可以看出机器人在越障过程中Mh始终位于给定的误差界内,机器人不会出现侧向倾斜现象,说明本文所提出的机构具备良好的转向越障能力,越障方式及算法可行。
5 结论
(1)本文提出了一种具有转向越障能力的三臂式巡检机器人机构,该机构能够通过调节机器人的姿态来满足越障过程中的重力平衡要求。
(2)针对三臂式巡检机器人重力平衡问题,给出了重力平衡约束条件及相应的越障算法。
(3)分析及仿真结果表明,本文所提出的机器人机构以及转向越障算法可以满足机器人转向越障过程中的重力平衡需求,机器人具有转向越障的能力。
[1]朱兴龙,周骥平,王洪光,等. 输电线巡检机器人越障机理与实验[J]. 机械工程学报,2009, 45(2): 119-125.
ZhuXinlong,ZhouJiping,WangHongguang,etal.ExperimentsandMechanismofObstacleNegotiationofAnInspectionRobotforTransmissionLines[J].JournalofMechanicalEngineering, 2009, 45(2):119-125.
[2]DebenestP,GuarnieriM,TakitaK,etal.Expliner-robotforInspectionofTransmissionLines[C]//IEEEInternationalConferenceonRoboticsandAutomation.Pasadena, 2008:3978-3984.
[3]朱兴龙,王洪光,房立金,等.输电线巡检机器人行走动力特性与位姿分析[J].机械工程学报,2006,42(12): 143-150.
ZhuXinlong,WangHongguang,FangLijin,etal.AnalysisofMovingDynamicPerformanceandPoseofanInspectionRobotforTransmissionLines[J].JournalofMechanicalEngineering, 2006, 42(12):143-150.
[4]WuGP,XiaoH,XiaoXH,etal.TransmissionLineInspectionRobotandDeicingRobot:KeyTechnologies,PrototypesandApplications[C]//1stInternationalConferenceonAppliedRoboticsforthePowerIndustry.Montreal, 2010:1-6.
[5]Pouliot N, Montambault S.Field-oriented Developments for Line Scout Techhnology and Its Deployment on Large Water Crossing Transmission Lines[J].Journal of Field Robotics,2012,29(1):25-46.
[6]Toth J, Pouliot N, Montambault S. Field Experiences Using Line Scout Technology on Large BC Transmission Crossings[C]//1st International Conference on Applied Robotics for the Power Industry.Montreal, 2010:1-6.
[7]Aoshima S, Takeshi T, Tetsure Y. A Wire Mobile Robot Multi-unit Structure[C]//IEEE/RSJ International Workshop on Intelligent Robots and Systems. Tsukuba, 1989:414-421.
[8]房立金,陶广宏. 新型多单元串联巡检机器人机构研究与设计[J]. 东北大学学报(自然科学版),2014, 35(8):1173-1178.
Fang Lijin, Tao Guanghong. Research and Design of a Novel Inspection Robot Mechanism with Multi-unit in Series[J]. Journal of Northeastern University(Natural Science), 2014, 35(8):1173-1178.
[9]Wang Jidai, Sun Aiqin, Zheng Candong, et al. Research on a New Crawler Type Inspection Robot for Power Transmission Lines[C]//1st International Conference on Applied Robotics for the Power Industry.Montreal, 2010:1-5.
[10]Yang Dewei, Feng Zuren, Ren Xiaodong, et al. A Novel Power Line Inspection Robot with Dual-parallelogram Architecture and Its Vibration Suppression Control[J].Advanced Robotics, 2014,28(12):807-819.
[11]Liang Qiaokang, Wang Yaonan, Zhang Dan,et al. Multifunctional Robotic System for Live Power Transmission Lines[J]. International Journal of Robot and Automation, 2014,29(2):175-183.
(编辑陈勇)
Gravity Balance and Steering and Obstacle-crossing of Three-arm Inspection Robots
Tao GuanghongFang Lijin
Northeastern University,Shenyang,110819
A novel three-arm inspection robot for power transmission line was proposed, which was composed of four serial parallelogram mechanisms. The robot mechanism possessed the ability to meet the gravity balance requirements when steering and crossing obstacles by adjusting the robot pose. The obstacle-crossing flows were presented, the pivotal step of steering obstacle-crossing was analyzed, the binary approximating principles were applied to search the robot obstacle-crossing pose satisfing the balance constraints.The solution method satisfing the balance constraints of the robot inverse kinematics was proposed,the robot steering and crossing obstacles under gravity balance conditions was realized. The research results show that the novel three-arm inspection robot has steering and obstacle-crossing capacity.
gravity balance; steering; obstacle-crossing; inspection robot
2015-06-12
辽宁省高等学校创新团队项目(LT2014006)
TP273
10.3969/j.issn.1004-132X.2016.09.003
陶广宏,男,1987年生。东北大学机械工程与自动化学院博士研究生。主要研究方向为机器人机构学。房立金,男,1965年生。东北大学机械工程与自动化学院教授、博士研究生导师。
