基于EEMD和MFFOA-SVM滚动轴承故障诊断
2016-09-05褚东亮毛新华
何 青 褚东亮 毛新华
华北电力大学, 北京,102206
基于EEMD和MFFOA-SVM滚动轴承故障诊断
何青褚东亮毛新华
华北电力大学, 北京,102206
针对滚动轴承发生故障时,振动信号的时域和频域特征都会发生变化的特点,提出了基于集合经验模态分解(EEMD)、改进果蝇优化算法(MFFOA)和支持向量机(SVM)的滚动轴承故障诊断方法。该方法主要是利用EEMD方法对故障信号进行分解,并计算各IMF分量的均方根值和重心频率,以此进行归一化处理得到特征向量。为了提高诊断精度,采用果蝇优化算法优化SVM参数,建立MFFOA-SVM模型,然后对提取的特征向量进行训练与测试,从而识别故障与否及发生点蚀故障的程度。利用该方法对实测信号进行分析与诊断,并与遗传算法的优化结果进行对比,验证了该方法的有效性,说明其具有良好的应用前景。
集合经验模态分解;改进果蝇优化算法;支持向量机;滚动轴承;故障诊断
0 引言
滚动轴承是各种旋转机械中应用最广泛的一种通用部件,也是最容易损坏的部件之一,其运行状态往往直接影响整台机器的性能,一旦滚动轴承出现故障就会造成巨大的经济损失,因此必须对其进行监测和诊断[1]。
对于传统的故障诊断方法,通过时域或频域分析对滚动轴承工作状态进行精确诊断是比较困难的[2]。近年来,许多学者对滚动轴承故障诊断方法进行了研究。于德介等[3]首次阐述了内禀模态函数(intrinsic mode function,IMF)分量在机械故障诊断中的应用,将M距离函数和支持向量机(support vector machine,SVM)进行结合,实现了故障模式识别。虽然SVM能够实现小样本识别分类且克服了神经网络局部极小值、结构和类型过分依赖于经验等缺点,但是,SVM需要通过核参数将特征向量映射到高维空间,其核参数和惩罚参数选择正确与否会影响到分类结果与精度。张涛等[4]将内禀模态特征能量法分别与SVM和神经网络结合,将其应用于滚动轴承故障模式识别,结果表明,与 SVM 相结合的诊断识别率高于神经网络的诊断识别率,但是对滚动轴承故障诊断识别率也仅为85%,主要是因为SVM分类器核参数的选择依赖于经验,常常得不到优化的核参数,导致识别率较低。
为了提高滚动轴承故障诊断的识别率,本文提出基于集合经验模态分解(ensemble empirical mode decomposition,EEMD)和改进果蝇优化算法(modified fruit fly optimization algorithm,MFFOA)和支持向量机的滚动轴承故障诊断方法。利用EEMD分解故障信号,选择IMF分量的均方根值和重心频率作为特征向量;利用MFFOA对SVM分类器的核参数和惩罚参数进行优化;利用MFFOA-SVM模型对所提取的实测信号的特征向量进行训练和测试,并将其分别与EEMD和MFFOA-SVM的诊断预测结果进行对比。
1 集合经验模态分解
EEMD分解法是对原始经验模态分解(empirical mode decomposition,EMD)[5-7]方法的重大改进。这种方法通过给信号加入极小幅度的白噪声,利用白噪声频谱均衡分布的特点,用白噪声来均衡噪声的特性,较为理想地解决了模态混叠问题。具体步骤如下:
(1)在原始信号x(t)中多次加入等长度的正态分布的白噪声ni(t),即
xi(t)=x(t)+ni(t)
(1)
式中,xi(t)为第i次加入白噪声后的信号。
(2)将添加了白噪声的信号通过EMD算法进行分解,得到IMF分量Cij(t)和余项ri(t),其中Cij(t)表示第i次加入白噪声后分解所得的第j阶IMF分量。
(3)利用不相关随机序列的统计均值为零的原理,将各分量Cij(t)进行整体平均以抵消多次加入白噪声对真实IMF分量的影响,得到最终EEMD分解结果,即
(2)
式中,Cj(t)为对原始信号进行EEMD分解得到的第j个IMF分量;N为添加白噪声序列的数目。
此时EEMD分解的结果为
(3)
IMF分量Cj(t)(j=1,2,…)主要是信号从高到低不同频段的成分信息,并且每个频段包含着不同的频率成分和能量,二者都会随着振动信号x(t)的变化而改变。
2 果蝇算法与支持向量机
2.1果蝇算法原理

图1 果蝇群体迭代搜索食物示意图
根据果蝇的基本生理特性,仿真模拟其寻找食物的全过程,进而获取具有良好全局性能的寻优方法[8]。对于果蝇来说,果蝇与食物之间的距离越远,其味道就越小,否则反之。因此,果蝇搜寻食物的过程就是不断地从味道小的地方到达味道更浓的地方的过程。如图1所示,n只果蝇从果蝇群体初始位置沿着随机方向飞出,然后所有果蝇再飞往味道浓度最高的果蝇位置,形成新的果蝇群体位置,再飞出,不断反复循环,直到找到食物源位置为止[9-10]。
与其他演化算法基本相似,果蝇算法在寻优的过程中具有一定的随机性,因此,该算法引入了同其他演化算法的适应函数的功能基本类似的味道浓度判定值和味道浓度判定函数,以便于准确地引导果蝇群体朝着正确的方向飞去,具体过程如图2所示。
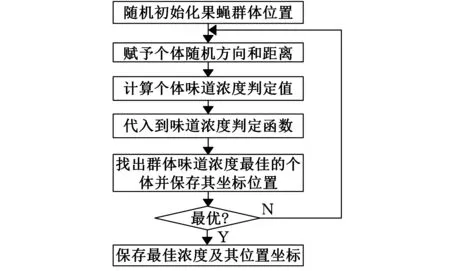
图2 果蝇优化算法流程图
依照果蝇觅食的习性可以将果蝇优化算法表述成以下几个必要的步骤[11]:
(1)随机初始化果蝇群体的坐标位置,得到初始坐标(X,Y) 。
(2)根据果蝇觅食行为的不同赋予其随机方向和距离,具体的随机距离按照初始坐标的位置来选择:
Xi=X+Lr,Yi=Y+Lr
其中, Lr为在固定步长区间[-L,L]内随机生成的步长值,可由Lr=L×rand(1,1)求得;L为果蝇个体利用嗅觉搜索的固定步长值。
(3)估计果蝇个体位置与坐标原点之间的距离Di,取距离的倒数作为果蝇味道浓度的判定值Si:
(4)
(4)将其果蝇味道浓度的判定值Si代入味道浓度的判定函数(或称为适应度函数)Fitness, 求出果蝇个体位置的味道浓度Smelli,即Smelli=Fitness(Si)。
(5)根据果蝇初始味道浓度值,寻找该果蝇群体中味道浓度的极值(最优个体)bestSmell=max(Smelli) 或bestSmell=min(Smelli),同时保留其极值的迭代次数bestIndex。
(6)利用视觉寻找果蝇聚集味道浓度的最佳值,记录果蝇此时的X、Y坐标和最优浓度bestSmell,并将其最佳味道浓度赋予Smellbest进行保留。果蝇的X、Y坐标为
(5)
(7)进入果蝇迭代寻优,重复执行步骤(2)~(5),在保证果蝇迭代次数小于设定的最大迭代次数gmax前提下,判断味道浓度是否优于前一次迭代味道浓度,若是,则执行步骤(6)。
2.2改进果蝇算法
在果蝇算法步骤(2)中,步长L设为固定值,即在每次觅食迭代中,果蝇个体以固定步长进行随机搜索。在果蝇群体个数一定的情况下,若步长值过小,则果蝇个体的局部寻优能力较强,搜索空间较小,全局搜索能力较弱,果蝇个体容易陷入局部最优;反之,若步长值过大,则果蝇个体的搜索空间变大,全局搜索能力变强,但是局部寻优能力减弱。可见,在传统果蝇算法中,如何正确地选择步长参数会直接影响算法的执行效率。
因此,在运用果蝇算法解决实际问题时,为了避免全局搜索能力陷入局部最优,提出了改进果蝇优化算法MFFOA。具体改进部分如下:
(6)
式中,L0为初始步长值;Imax为最大觅食迭代次数;I为当前觅食迭代次数;L为递减步长值。
当第1代果蝇觅食时,令L=L0,果蝇个体步长为最大值L0。随后果蝇觅食迭代每增加1代,步长就减小L0/Imax,直到最后一代减到L0/Imax为止。
因此,MFFOA在迭代早期搜索步长最大,且搜索空间也大,全局寻优能力最强。随着觅食迭代次数的不断增加,该算法的局部搜索能力也在逐渐增强,能够提高觅食早期全局最优解的概率,避免陷入局部最优,觅食末期能够达到最大的搜索精度,从而实现全局搜索能力和局部寻优能力的平衡。
2.3支持向量机原理
统计学习理论[12]提出,把函数集构造为一个函数子集序列,使各个子集按照置信风险的大小排列;在每个子集中寻找最小经验风险,通常它随着子集复杂程度的增加而减小。折中考虑经验风险和置信风险,使得实际风险最小,这就是结构风险最小化原则, 它改变了传统的经验风险最小化原则,在预测性能方面明显优于神经网络法[13-14]。
通过非线性映射的函数,得到满足多维样本输入、一维样本输出原则的向量,将其作为输入向量从原来的空间映射到高维特征空间H,并在该特征空间H内建立优化超平面,分类线方程如下[15-16]:
ω·x+b=0
(7)
式中,ω为权值矢量;x为输入向量;b为阈值。
并且使得该超平面将两类不同的样本正确地分类,此外,还应使该超平面满足如下的约束条件:
yi[ω·xi+b]≥1i=1,2,…,l
(8)
式中,l为支持向量的数目。
从而得到分类间隔最大的超平面,也就是最优分类面,如图3所示。
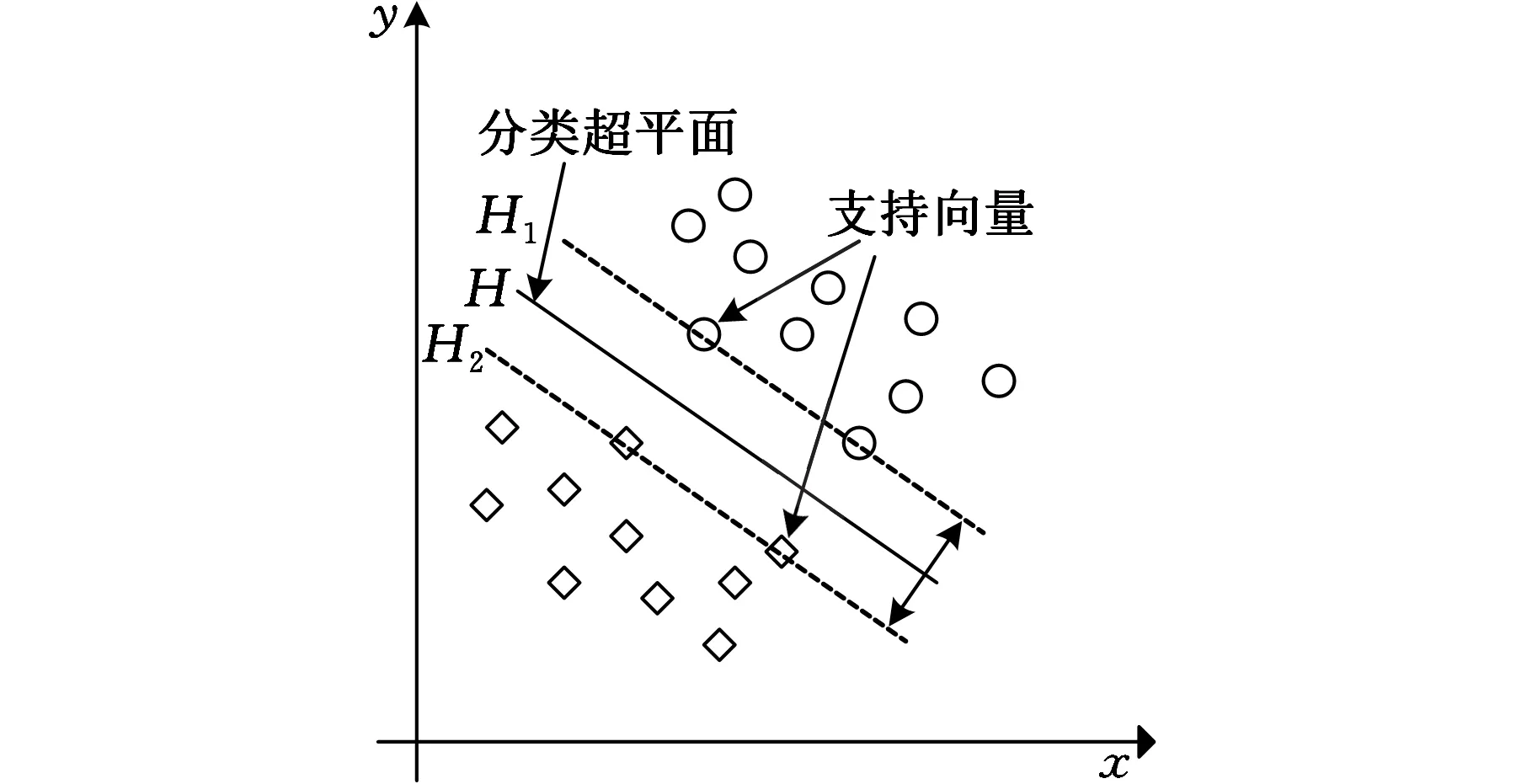
图3 支持向量机的最优分类面
引入非负的松弛变量ξ、惩罚因子C、Lagrange乘子ai等参数,将约束优化问题转化为如下问题:
(9)
根据Karush-Kuhn-Tucker的条件,优化系数满足如下条件:
ai{yi[ω·xi+b]-1+ξi}=0
(10)
通过求解上述问题,最终可得到最优分类函数:
(11)
式中,σ(x,xi)为核函数。
适应度函数为
(12)
R(σ2,C)为训练样本的均方根误差:
(13)
综上所述,惩罚参数C和核函数参数σ是影响SVM分类器性能的关键参数,因此以(C,σ)作为寻优变量。
2.4MFFOA-SVM模型
通过MATLAB建立MFFOA-SVM模型,如图4所示。

图4 MFFOA-SVM训练步骤
可以将MFFOA-SVM模型表述成以下几个必要的步骤[17]:
(1)设定果蝇群体数目Spop,迭代次数gmax。由于优化参数有2个,所以初始果蝇位置时,X、Y应分别取2个随机数,对每个果蝇觅食的飞行方向和距离赋值,得到初始坐标(X1,Y1), (X2,Y2)。估计果蝇个体位置与坐标原点之间的距离,得到果蝇味道浓度的判定值S1i、S2i。
(2)适当地选择判定值的大小以确定惩罚因子C、核函数σ的取值范围,C=mS1i,σ=nS2i。根据C、σ的取值范围来调整m、n的取值大小。本文分别取C∈[0,1000],σ∈[0,100],为了让S的定义域被限制在[0,10]之间,取m=100,n=10。
(3)对数据集特征值进行SVM 模型训练,得到适应度函数f。
(4)果蝇浓度最高的位置即为f的最大值,保留该果蝇的坐标值,设为初始最佳坐标值。
(5)进入迭代寻优过程,保留最佳适应度函数和C、σ的参数值。此时应该注意,最佳的适应度对应多个C、σ的值,当C过大时,会造成误差增大,因此保留最小的C以及对应的σ值。
3 实测信号诊断设计
为了验证所提出方法的有效性,对来自美国Case Western Reserve University滚动轴承数据中心的实验数据进行分析。该实验测试平台主要由驱动电机、转矩传感器、测力计和电子控制装置组成,而驱动端和风扇端电机轴承分别包含型号为SKF6025-2RS和SKF6203-2RS的深沟球轴承,驱动端和风扇端轴承尺寸信息如表1所示[18]。

表1 滚动轴承参数
3.1信号数据说明
本文测试轴承为SKF6025-2RS深沟球轴承。对采样频率12 kHz、转速1772 r/min时的故障数据进行分析。点蚀直径不同,滚动轴承的故障程度不同,本文以点蚀直径0.18 mm代表故障早期或者轻微故障,以点蚀直径0.71 mm代表故障晚期或者严重故障。
由于故障特征参数不仅与故障类型有关,还与故障程度有关,也就是说同种故障不同程度,其特征参数规律也不相同,因此根据此特征,将测试信号分为8组,定义为类别标签,每一组对应不同故障类型的不同程度。
这样分类主要是考虑到误差问题。如果某一个6组信号被识别成8组信号,则这个结果在8组分类中是错误的,但是从故障类型的角度来分析,这种“错误”是可以接受的,因为6、8组都属于外圈故障,如表2所示。

表2 滚动轴承数据分组
3.2故障诊断流程
具体故障诊断流程如图5所示,即采用EEMD方法对滚动轴承振动信号进行归一化处理,然后求出IMF分量的均方根值和重心频率,组成故障特征向量,以MFFOA-SVM模型作为分类器来识别滚动轴承的工作状态和故障类型[19-20]。

图5 故障诊断流程图
4 实测信号诊断分析
进行8组分类故障识别,其中正常取80组数据,内圈故障按照4种不同故障程度分别取40组数据,共160组数据;外圈故障按照3种不同故障程度分别取40组数据,共120组数据;总计360组数据。不同状态的数据均等分为两部分,一半输入MFFOA-SVM作为训练样本进行学习,另一半作为测试样本用来识别。
4.1时域-频域多参数诊断
建立时域和频域多参数特征向量,考虑到运算效率,从时域特征参数与频域特征参数中分别提取均方根值和重心频率,进行故障模式识别。
在识别前,对果蝇优化算法的参数进行设定,初始化果蝇群体设置区间为[0,1],种群规模为20,迭代次数为100。MFFOA的搜寻结果发现,最佳的C=11.7769,最佳的σ=0.01。果蝇算法寻找最佳参数的进化迭代过程如图6所示。

图6 MFFOA寻找最佳参数的适应度曲线图

图7 EEMD时域和频域多参数的诊断分类图(MFFOA-SVM)

图8 EMD时域和频域多参数的诊断分类图(MFFOA-SVM)
通过MFFOA优化SVM最佳参数,可以得到EEMD和EMD时域和频域多参数的诊断分类图,见图7和图8。由图7可知,内圈中有一个样本被分错,其余样本的诊断结果完全正确;而图8显示,外圈和内圈分别有三个样本和一个样本被分错,其余的全部诊断正确。经过对比,发现 EEMD时域和频域多参数的诊断效果要优于EMD时域和频域多参数的诊断效果。
4.2诊断结果分析
根据故障诊断流程,利用MFFOA优化SVM最佳参数,可以求出EEMD分解后的各IMF分量的均方根值与重心频率两种特征,前后排列作为特征向量进行诊断。具体分类准确率见表3。

表3 时域和频域多参数分类准确率(MFFOA-SVM)
由表3数据可知,EEMD和EMD时域频域多参数的整体诊断准确率都在97%以上,说明该方法是有效的。而EEMD分类诊断准确率要比EMD分类诊断准确率高2%左右。
在内圈故障中, EEMD和EMD的故障诊断准确率是一致的,但是对点蚀故障程度的识别是不同的。EMD对点蚀直径0.71 mm故障的诊断准确率是95%,而EEMD对点蚀直径0.36 mm的诊断准确率是95%。
在外圈故障中,EEMD分解外圈故障的诊断准确率是100%,比EMD分解外圈故障的诊断准确率要高出很多。EMD分解对点蚀故障程度诊断准确率最低是90%。
对比遗传算法(GA)优化SVM最佳参数,可以得到EEMD时域和频域多参数的诊断分类图,如图9所示。由图9可知,外圈中有两个样本出现故障,其余的诊断结果完全正确。同时,可以求出EEMD时域和频域多参数的分类准确率,见表4。由表4可知,在内圈故障中,EEMD分解的诊断准确率为100%;在外圈故障中,EEMD对点蚀直径为0.71 mm故障的识别率为90%。

图9 EEMD时域和频域多参数的诊断分类图(GA-SVM)
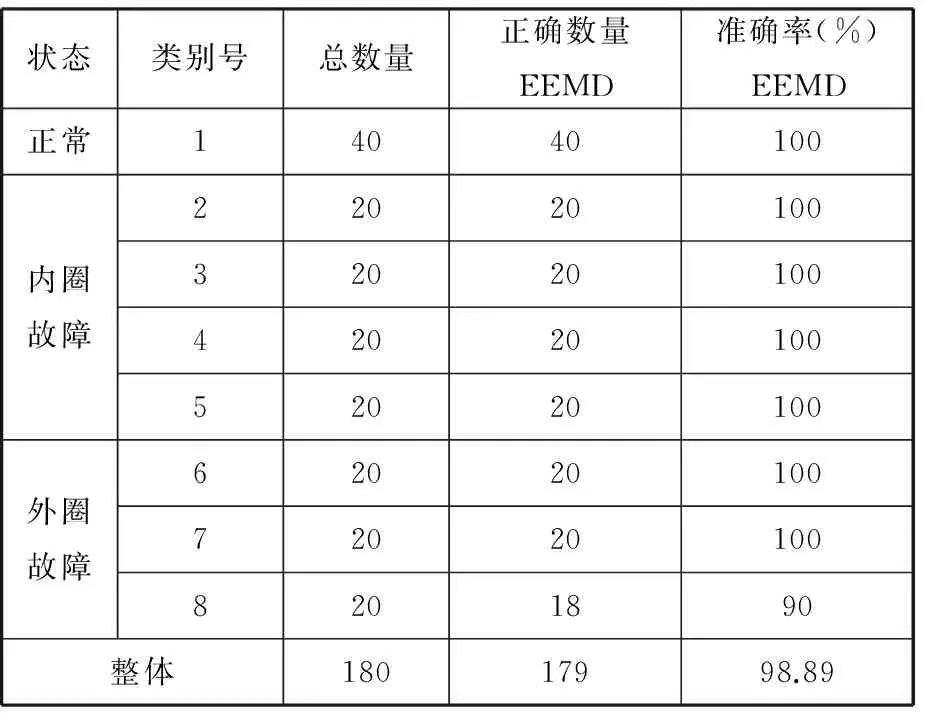
状态类别号总数量正确数量EEMD准确率(%)EEMD正常14040100内圈故障22020100320201004202010052020100外圈故障62020100720201008201890整体18017998.89
基于训练样本数据,分别使用MFFOA和GA优化SVM回归模型参数C和σ进行对比。表5所示为实测信号优化结果的定量对比,图10为典型的实测信号分析中算法寻优进化曲线对比图。由分析可见,MFFOA的寻优准确率要高于GA的寻优结果,且运行时间较短。
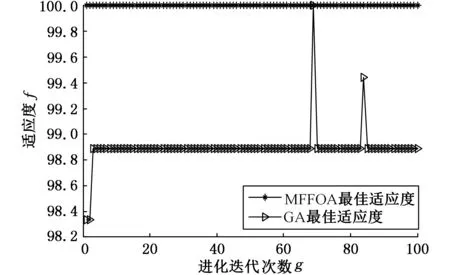
图10 实测信号分析中算法适应度曲线

算法迭代次数种群大小模型平均训练时间(s)准确率(%)MFFOA10020102.5799.44GA10020136.3998.89
5 结论
(1)使用具有全局搜索能力的MFFOA对SVM进行特征选择与参数优化,可以提高SVM分类器的分类能力。
(2)基于EEMD和MFFOA-SVM的故障诊断准确率明显高于EMD和MFFOA-SVM的故障诊断准确率,表明EEMD分解得到的IMF分量对轴承故障诊断更有效。
(3)与GA-SVM算法相比,基于EEMD和MFFOA-SVM模型的轴承故障诊断方法具有更加准确的分类效果和更高的诊断精度,该方法也可以应用于其他机械零部件的故障诊断。
[1]丁康, 孔正国. 振动调幅调频信号的调制边频带分析及其解调方法[J]. 振动与冲击, 2006, 24(6): 9-12.
DingKang,KongZhengguo.ModulationVibrationAmplitudeModulationFrequencyModulationSignalSidebandAnalysisandDemodulationMethod[J].Vibration&Shock, 2006, 24(6): 9-12.
[2]TandonN,ChoudhuryA.AReviewofVibrationandAcousticMeasurementMethodsfortheDetectionofDefectsinRollingElementBearings[J].TribologyInternational, 1999, 32: 469-480.
[3]于德介, 程军圣, 杨宇. 机械故障诊断的Hilbert-Huang变换方法[M]. 北京: 科学出版社, 2006.
[4]张 涛, 陆森林, 周海超, 等. 内禀模态特征能量法在滚动轴承故障模式识别中的应用[J]. 噪声与振动控制, 2011, 31(3): 125-128.
ZhangTao,LuSenlin,ZhouHaichao,etal.ApplicationofIntrinsicModeFunctionFeatureEnergyMethodinFaultPatternRecognitionofRollingBearing[J].NoiseandVibrationControl, 2011, 31(3): 125-128.
[5]HuangE,ShenZheng,LongSR,etal.TheEmpiricalModeDecompositionandtheHilbertSpectrumforNonlinearandNon-stationaryTimeSeriesAnalysis[J].Proc.R.Soc.Lond.A, 1998, 454(12): 903-995.
[6]张俊红, 李林洁, 马文朋,等.EMD-ICA联合降噪在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2013, 24(11): 1468-1472.
ZhangJunhong,LiLinjie,MaWenpeng,etal.ApplicationofEMD-ICAtoFaultDiagnosisofRollingBearing[J].ChinaMechanicalEngineering, 2013, 24(11): 1468-1472.
[7]孟宗,李姗姗. 基于小波半软阈值和EMD的旋转机械故障诊断[J]. 中国机械工程,2013,24(10):1279-1283.
MengZong,LiShanshan.ResearchonFaultDiagnosisforRotatingMachineryBasedonSemi-softWaveletThresholdandEMD[J].ChinaMechanicalEngineering, 2013, 24(10): 1279-1283.
[8]潘文超. 果蝇最佳佳演化算法[M]. 台北: 沧海书局, 2011.
[9]LiH,GuoS,ZhaoH,etal.AnnualElectricLoadForecastingbyaLeastSquaresSupportVectorMachinewithaFruitFlyOptimizationAlgorithm[J].Energies, 2012,5(11): 4430-4445.
[10]LiHZ,GuoS,LiCJ,etal.AHybridAnnualPowerLoadForecastingModelBasedonGeneralizedRegressionNeuralNetworkwithFruitFlyOptimizationAlgorithm[J].Knowledge-BasedSystems, 2013, 37, 378-387.
[11]牛培峰, 麻红波, 李国强, 等. 基于支持向量机和果蝇优化算法的循环流化床锅炉NOx排放特性研究[J]. 动力工程学报, 2013, 33(4): 267-271.
NiuPeifeng,MaHongbo,LiGuogiang,etal.StudyonNoxEmissionfromCFBBoilersBasedonSupportVectorMachineandFruitFlyOptimizationAlgorithm[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(4): 267-271.
[12]章永来, 史海波, 周晓峰, 等. 基于统计学习理论的支持向量机预测模型[J]. 统计与决策, 2014(5): 72-74.
ZhangYonglai,ShiHaibo,ZhouXiaofeng,etal.SupportVectorMachinePredictionModelBasedonStatisticalLearningTheory[J].StatisticsandDecision, 2014(5): 72-74.
[13]杨金芳, 翟永杰, 王东风, 等. 基于支持向量回归的时间序列预测[J]. 中国电机工程学报, 2005, 25(17): 110-114.
YangJinfang,ZhaiYongjie,WangDongfeng,etal.TimeSeriesPredictionBasedonSupportVectorRegression[J].ProceedingsoftheCSEE, 2005, 25(17): 110-114.
[14]谢宏, 魏江平, 刘鹤立. 短期负荷预测中支持向量机模型的参数选取和优化方法[J]. 中国电机工程学报, 2006, 26(22): 17-22.
XieHong,WeiJiangping,LiuHeli.ParameterSelectionandOptimizationMethodofSVMModelforShort-termLoadForecasting[J].ProceedingsoftheCSEE, 2006, 26(22): 17-22.
[15]丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011(1): 2-10.
DingShifei,QiBingjuan,TanHongyan.AnOverviewonTheoryandAlgorithmofSupportVectorMachines[J].JournalofUniversityofElectronicScienceandTechnology, 2011(1): 2-10.
[16]叶林, 刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报, 2011, 31(31): 102-108.
YeLin,LiuPeng.CombinedModelBasedonEMD-SVMforShort-termWindPowerPrediction[J].ProceedingsoftheCSEE, 2011, 31(31): 102-108.
[17]ZhangJ,WangR,LiJ,etal.FruitFlyOptimizationBasedLeastSquareSupportVectorRegressionforBlindImageRestoration[C]//InternationalSymposiumonOptoelectronicTechnologyandApplication2014.Beijing:InternationalSocietyforOpticsandPhotonics, 2014: 93011W-93011W-8.
[18]LoparoKA.TheCaseWesternReserveUniversityBearingDataCenter[EB/OL]. [2012-11-15].http: //csegroups.ase.edu/hearingdatacenter/pages/download-data-file.
[19]RenY,SuganthanPN,SrikanthN.AComparativeStudyofEmpiricalModeDecomposition-basedShort-termWindSpeedForecastingMethods[J].SustainableEnergy, 2015, 6(1): 236-244.
[20]YangCY,WuTY.DiagnosticsofGearDeteriorationUsingEEMDApproachandPCAProcess[J].Measurement, 2015, 61: 75-87.
(编辑苏卫国)
Study on Rolling Bearing Fault Diagnosis Based on EEMD and MFFOA-SVM
He QingChu DongliangMao Xinhua
North China Electric Power University, Beijing, 102206
Both of the time domain and frequency domain of the vibration signals would be changed when rolling bearing faults occured. A rolling bearing fault diagnosis method was proposed based on EEMD, MFFOA and SVM. EEMD was used to decompose the fault signals, and to calculate the root mean square value and frequency of the center of gravity, achieving the normalization processing feature vector. In order to improve the classification accuracy rate, a MFFOA-SVM model was built, and then the feature values were extracted for training and testing, so that it might recognize the faults or not and the degree of pitting corrosion failures. The actual signals were analyzed and diagnosed, and compared with genetic algorithm optimization results, it proves the validity of the method, and the improved method has a good prospect for its applications in rolling bearing diagnosis.
ensemble empirical mode decomposition(EEMD); modified fruit fly optimization algorithm(MFFOA); support vector machine(SVM); rolling bearing; fault diagnosis
2015-07-13
中央高校基本科研业务费专项资金资助项目(2014XS25,2014MS17)
TH113.2;TB533
10.3969/j.issn.1004-132X.2016.09.009
何青,男,1962年生。华北电力大学能源动力与机械工程学院教授、博士研究生导师。研究方向为振动工程与测试技术、状态监测与故障诊断。褚东亮,男,1984年生。华北电力大学能源动力与机械工程学院博士研究生。毛新华,男,1975年生。华北电力大学能源动力与机械工程学院博士研究生。
