基于异质性投资者的动态情绪资产定价①

曾　燕, 康俊卿, 陈树敏

(1. 中山大学岭南(大学)学院, 广州 510275; 2. 广东工业大学管理学院, 广州 510520)



基于异质性投资者的动态情绪资产定价①

曾燕1, 康俊卿1, 陈树敏2*

(1. 中山大学岭南(大学)学院, 广州 510275; 2. 广东工业大学管理学院, 广州 510520)

沿用基于消费的资产定价模型设定, 将行为金融领域中离散时间框架下的情绪资产定价模型拓展到连续时间框架下, 把异质性纳入Lucas纯交换经济体, 构建了一个含有异质性投资者的动态情绪资产定价模型, 并使用中央计划者问题求解出异质均衡.通过加入投资者情绪因子, 本文得到情绪投资者的主观股利增长率,并将其用于动态异质情绪资产定价模型的框架中, 以此刻画理性投资者和情绪投资者的异质性,研究结果表明投资者情绪是影响收益的重要因子.数值算例与敏感性分析表明投资者关于股利信息的错误预期将会导致横截面股价漂移率增大.

行为金融; 异质性定价; 情绪定价模型

0　引　言

资产定价、资产配置和风险管理是现代金融学的核心.在现代金融学中, 标准的资产定价模型以有效市场假设为基础, 并认为“所有投资者是同质的”.这要求不同投资者接收到的信息是完全对称的且对信息的反映一致. 简单的同质性假设使得问题更易于求解及验证, 但所导出的结论却受到超额波动率之谜[1]、股权溢价之谜[2]等实证结果强有力的挑战.大量金融异象迫使经济学家们思考新的定价范式以寻求对实证异象的合理解释,其中一些学者着眼于行为资产定价[3, 4].

在投资者有限理性的假定下, 行为资产定价模型借助有限套利和投资者有限理性这两个重要因素对经典资产定价体系所面临的挑战进行解释, 其结果在股票截面期望收益等领域得到很好的运用, 并形成了一系列具有代表性的行为资产定价模型.结合熊和平等[5, 6], 本文将各类行为资产定价模型归类为*详见附录表格1.: 1)以基于效用函数修正的资产定价模型与异质性投资者的定价模型为代表的修正传统理性经济人定价范式; 2)以基于个人反应的行为资产定价模型与基于市场反应的行为资产定价模型为代表的基于经济人行为定价范式; 3)基于计算实验金融的定价范式.

近年来, 修正的传统理性经济人定价范式被主流金融经济学所偏爱, 经济学家们往往在传统定价模型基础上进行修正,如基于效用函数修正的定价模型和异质性投资者的定价模型[6].本文设定的行为资产定价模型试图把异质性纳入Lucas纯交换经济体系, 建立异质信念投资者的定价模型. 如今越来越多的学者研究异质信念投资者模型, 在早期的工作中, Harrison和Kreps[7], Varian[8,9], Abel[10], DeLong等[11]以及其他学者考虑了单期和多期离散时间模型; Williams[12], Wang[13]等考虑了连续时间模型, Zapatero[14]及Basak和Cuoco[15]对连续时间模型进行了拓展. 在此基础上, Basak[16]和Li[17]等借助异质信念资产定价模型对股权溢价之谜、无风险利率之谜、过度波动率之谜等做出了解释. Barberis等[3]考察了一个外推的资产定价模型, 假设市场上的投资者从过去的股价历史中推测未来的股市情况、这些“外推者”认为股票的预期价格变化是过去股价变化的加权平均, 并得到了均衡股价过程,从而更全面地解释了市场中存在的异象.

受到Barberis等[3]的启发, 本文将构建一个新的含异质性投资者的均衡股价模型,在模型中融入对股票收益率有着系统性影响的投资者情绪因子以分析情绪因子对均衡时股票收益率、波动率的作用路径及方式. 本文模型包含两类资产: 无风险资产和支付外生股利的风险资产, 其价格由市场均衡确定. 基于连续时间的纯交换经济框架, 假设两类代表性投资者(理性投资者和情绪投资者)的目标均是最大化其一生的消费效用, 他们之间的差异在于对股利运动过程的预期不同.情绪投资者受到投资者情绪的影响, 对股利过程漂移率的预期等于真实过程漂移率加上情绪函数; 理性投资者是完全理性的, 他们不仅了解真实股价运动过程, 并且知道情绪投资者如何形成投资情绪、如何依照投资情绪进行股票交易, 该模型设定与Barberis等[3]一致.研究结果表明, 投资者情绪对均衡时股价漂移率和波动率有显著的影响, 这表明投资者情绪是影响收益的一个系统性因子.

1　模型构建

本文研究一个包含两类投资者的纯交换连续时间完全竞争模型. 类似于Barberis等[3], 模型一个典型的特征就是其中一类投资者对于未来支付有错误的预期. 更进一步, 此类投资者对于股利支付预期带有Yang和Zhang[18]所定义的投资者情绪. 模型中可以将两类投资者视为机构投资者和个体投资者. 由于个体投资者缺乏相应的专业知识、专门机构的决策支持,其信息来源有限, 受媒体消息报道的影响较大并且缺少风险控制手段,故易受股市短期形势影响表现出投资者情绪. 本节将对总体禀赋、投资者情绪以及资本市场进行描述, 并构建行为主体的最优化模型.

1.1总体禀赋

考察Lucas纯交换经济, 假设经济体中存在一种风险资产, 支付的外生股利(即总体禀赋)δ(t)服从几何布朗运动

dδ(t)/δ(t)=μδ(t)dt+σδdZ1(t)

(1)

其中μδ(t)、σδ分别表示时刻t股利的漂移率和波动率, Z1(t)为一维标准布朗运动. 参照异质性投资者定价模型的基本假设[16,17], 不失一般性, 假定股利的波动率为外生常数.

假设经济体中有两类投资者:理性投资者和情绪投资者,理性投资者知道真实的股利运动过程; 情绪投资者会对所预期的股利过程产生异质信念, 即投资者情绪.情绪投资者的预期股利过程表示如下

dZ2(t)=dZ1(t)+β(t)dt

(3)

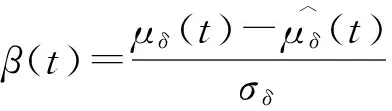
1.2投资者情绪

采用Yang 等[18]的方法定义情绪投资者对于股利过程漂移率的预期, 即假设

(4)

其中SI是投资者情绪, f(·)为情绪函数. 上述定义表明情绪投资者对所预期的股利发放带有情绪预期f(SI).变量SI反映了情绪交易者的看涨(或看跌)预期. 同时, 情绪函数f(·)是股利平均增长率的超额收益率, 且其函数值与自变量SI的符号值一致,即当投资者情绪乐观时f(SI)>0; 当投资者情绪悲观时f(SI)<0; 当投资者是完全理性时f(SI)=0.

1.3资本市场

在每个时刻, 行为主体需考虑消费与投资决策. 假设市场中风险资产将支付的股利由非负的随机过程δ(t)刻画, 这一过程是外生的, 由式(1)给定. 均衡时, 风险资产价格过程满足

(5)

其中S(t)、μ(t)、σS(t)分别表示时刻t的股价、漂移率、波动率. 这里将资产的股份数量正规化为1. 两类投资者同时观察到股利过程, 分别对股价做出如下推断

(6)

(8)

(9)

1.4行为主体的最优化

投资者i的投资-消费策略记为(πi,Ci)={(πi(t),Ci(t)),t∈[0,T]}, 即在时刻t消费金额为Ci(t), 投资在风险资产上的资金比例为πi(t), 投资到无风险资产上的资金比例为1-πi(t). 在该策略下投资者的预算约束可以表示为

Ci(t)]dt+πi(t)Wi(t)σS(t)dZi(t)

(10)

其中Wi(t)表示投资者i在时间t的财富值.

假设经济体中每类投资者都有跨期可加的消费效用函数

(11)

其中ρi>0是投资者i的主观贴现因子. i=1表示理性投资者、i=2表示情绪投资者. 依照本节开头的论述, 本文理性投资者可以视为机构投资者. 由于其资产规模大、持股数量多, 对公司实施监控的成本与收益的匹配度较好, 有能力和动力参与公司治理,故更倾向于充当积极股东、关心公司经营状况并进行长期投资[19].因此假设ρ1<ρ2, 其表示理性投资者更具有耐心, 更重视未来收益.

给定投资者的财富过程及效用函数, 两类投资者均需求解如下最优化问题

s.t.式(10)

异质模型的市场均衡可定义如下:

1)(Ci,πi)是对应优化问题(Pi)的最优策略;

2)均衡时一价定律成立, 股票市场不存在套利机会, 即

(12)

3)商品市场与证券市场出清条件成立

C1(t)+C2(t)=δ(t)

(13)

W1(t)+W2(t)=S(t)

(14)

由于均衡时资产的价格由两个异质投资者共同确定, 故市场均衡时每个投资者的跨期边际替代率(IMRS) 都可以作为有效的SDF进行资产定价[20]. 而另一种被学者们广泛采用的方式则是利用中央计划者问题求解均衡, 下文利用此方法求解均衡时股票的漂移率.

2　异质均衡

首先考察情绪投资者与理性投资者如何相互影响. 假设情绪投资者受到投资情绪的影响, 对未来的股利增长持悲观态度, 因此情绪投资者将会抛售所持有的股票, 导致股价下降(价格压力效应). 理性投资者知道真实的股利过程, 了解股价被低估, 故将增加股票持有量, 理性投资者的投资策略抵消了价格压力效应, 当理性者的需求量与情绪者的供给量一致时股价不变. 但类似于Barberis等[3],本文假设理性投资者是完全理性的, 他们所推测的均衡时股价不仅取决于真实股利过程, 还包含情绪投资者的投资情绪及投资策略的影响, 故其需求量与情绪投资者的供给量并不一致, 最终均衡时股价取决于两类投资者的供需均衡. 本节系统地分析投资者情绪对于均衡时股价过程的影响, 并对均衡时的股价漂移率进行讨论.

Ci(t)=Ii(yiζi(t))

(15)

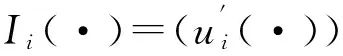
(16)

在下文求解过程中, 先考虑中央计划者问题, 求解两类投资者的投资、消费策略, 再通过本文对理性投资者的假定, 构建并求解均衡方程, 得到均衡时股价过程.

2.1中央计划者问题

当投资者存在异质性时, 资产定价问题往往采用一般均衡定价方法进行求解. 近年来, 越来越多的文献开始采用中央计划者问题替代一般均衡方法来求解异质性问题.早期对替代条件的研究可参考Rubinstein[22]等学者的工作.

本文设定的动态资产定价模型符合替代条件. 中央计划者目标是将总禀赋在不同的消费者之间进行分配, 使其达到Pareto最优.中央计划者的目标函数可表示为

(17)

Karatzas等[23]表明当投资者具有异质偏好、异质禀赋时,λ(t)为常数且由期初的预算约束决定. Basak和Cuoco[15]与Basak[16]考虑了当投资者有投资约束和投资者异质信念时的中央计划者问题, 指出λ(t)是一个随机加权因子, 且随机权重由一系列内生的变量决定.参照Basak[16]对λ(t)的描述可得

(18)

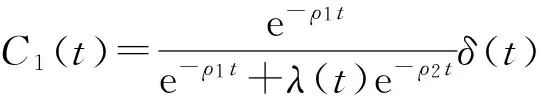
(19)

类似可得两类消费者的状态价格密度

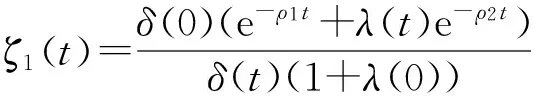
(20)

证明见附录.

引理1表明, 由于不同的投资者之间的异质信念,两类投资者在进行投资与消费决策时面临不同的状态价格密度,进一步使得Pareto最优时其权重也是随机的. 对于随机加权因子λ(t)求微分, 不难得出dλ(t)/λ(t)=-β(t)dZ1(t). 由此可见, 当β(t)增加时, λ(t)随之减小, 第一类消费者消费更多、第二类消费者消费更少.这表明随机加权因子将会使更为乐观的投资者在不确定性更强时消费越多.

2.2均衡资产定价方程

在引理1中, 求解的最优消费策略以及状态价格密度中含有λ(t), 即均衡时中央计划者的随机加权系数, 这将由动态预算约束决定. 为下文求解方便, 可利用求解出来的状态价格密度消去λ(t), 具体过程如下.由于

(21)

将其代入最优消费策略中, 可消去随机加权因子, 得到

C1(t)=δ(0)e-ρ1s/ε1(t)(1+λ(0))

(22)

C2(t)=δ(0)λ(0)e-ρ2s/ε2(t)(1+λ(0))

(23)

根据最优消费策略及投资者的预算约束可将财富过程表示为

(24)

(25)即均衡时两类投资者的财富可表示为未来的消费流的贴现值. 定义财富之比η(t)以及消费倾向之比Ω(t)为

(26)

W1(t)θ1(t)dZ1(t)

(27)

W2(t)θ2(t)dZ2(t)

(28)

其中θ1(t)、θ2(t)表示投资者的市场风险价格. 根据前文的假定, 理性投资者是完全理性的, 这意味着市场均衡时理性投资者不仅能够了解真实的股价运动, 即

(29)

而且知道情绪投资者的预期与投资策略. 由于财富过程依赖于投资策略, 理性投资者可以推测情绪投资者的财富过程

C2(t)]dt+W2(t)θ2(t)dZ1(t)

(30)

在本文所设定的经济体中将资产的股份数量正规化为1, 因此市场出清条件要求两类投资者的财富总和等于风险资产价格.根据式(5)和式(14)可得

dW1(t)+dW2(t)=(S(t)μ(t)-δ(t))dt+

S(t)σS(t)dZ1(t)

(31)

式(27)与式(30)相加, 然后将其漂移项与式(31)的漂移项对比, 可得

θ2(t)β(t)]-[C1(t)+C2(t)]

=(W1(t)+W2(t))μ(t)-δ(t)

(32)

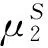
(33)

定理1均衡时股价过程的漂移率μ(t)为

(34)

理性投资者的风险资产持有量N1(t)为

(35)

其中A(t)=(1-Ω(t))η(t)/σδ(1+η(t))(1+Ω(t)η(t)).

证明见附录.

定理1表明投资者情绪对于均衡时股价漂移率有显著的影响,是影响收益的一个系统性因子.由式(34)可知, 当情绪投资者的乐观情绪上升时, 股票截面收益率上升, 这与张强和杨淑娥[24]的结论一致.此外, 值得注意的是当投资者的悲观情绪上升时, 股票截面收益率也同样会随之上升,下文结合敏感性分析和现有文献对这一现象做出详细解释.

3　敏感性分析

本节分析投资情绪对股票截面收益率、波动率的影响,且考虑无风险利率、投资者财富比例、投资者消费倾向比例等发生变化时的情形,给出相应数值算例.

3.1基本分析

下文结合定理1分析投资者情绪对均衡时股价漂移率的影响, 并对所得结论做出合理的解释. 为了定量分析投资者情绪对均衡时股价的影响, 考虑f(SI)=exp(C*SI)-1. 依照Yang和Zhang[18]对于参数的选取, 对基本参数做如下设定: σδ=15%;C=0.1;r=10%.此外, Yang和Zhang[18]设定SI∈[-6,6], 本文适当缩小投资情绪波动的范围, 定义SI∈[-4,4]. 同时由于下文将对财富之比、消费倾向之比做敏感性分析, 不失一般性, 在此设定Ω(t)=0.3,η(t)=5.

图1描绘了上述参数选择下投资者情绪SI对均衡时股价过程漂移率的影响. 不难看出,随着乐观情绪的上涨均衡的股价漂移率也上涨; 另一方面, 随着情绪投资者的悲观情绪上升,未来的均衡时股票收益率也会上升. 同时,与悲观情绪相比乐观情绪对均衡时股价漂移率的影响更加敏感.这一结果表明投资者情绪是影响股票收益的一个系统性因子.

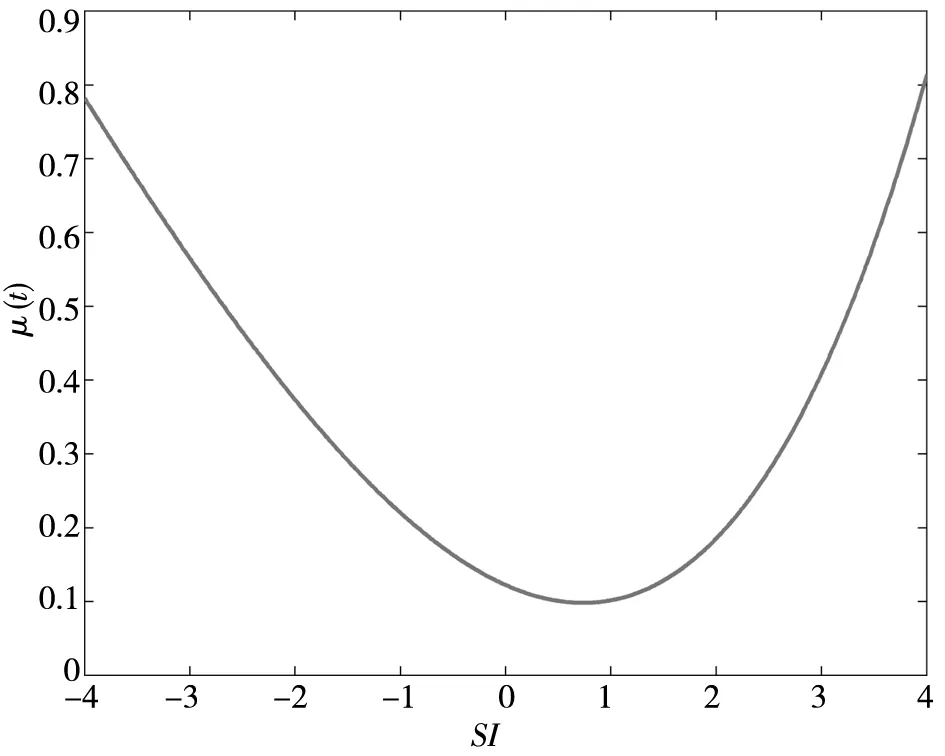
图1　投资者情绪对均衡时股价漂移率的影响

张强和杨淑娥[24]将投资者情绪分为上涨和下降, 分别回归时发现随着投资者情绪上涨, 股价上涨, 收益率也随之增加; 随着投资者情绪下降, 股价下降, 收益率为负. 此类文献发现当情绪投资者对未来预期悲观时,股票的横截面收益率会下降,这与本文结论相反. 以下结合图2所述影响路径对这一现象进行解释.当投资者预期悲观时,将引致对股价做出错误估值,此时价格压力效应发生作用,情绪投资者抛售股价引致截面股价收益率降低. 但正如王美今和孙建军[26]所提及的, 尽管潜在的价格压力效应存在,但其对均衡时股价的影响并不确定. 原因在于均衡时股价的形成还受到其他交易者需求量的影响.DeLong等[11]在噪音交易模型中指出挤出效应的存在, 即投资者的投资情绪放大了不确定性,因此“挤出”了市场中的理性投资者,降低了股价. 但在本文的设定中,挤出效应并不显著. 由上节定理1可知, 当投资者情绪悲观放大时, 理性投资者非但没有被“挤出”, 其风险资产持有量还随之上升. 这一现象是由于在本文的设定中, 理性投资者不仅知道真实的股利及股价运动过程,也知道情绪投资者的投资情绪及均衡时股价形成过程. 因此, 理性投资者一旦发现情绪投资者过度低估股票价值, 将会增持股票, 理性投资者的这一行为一定程度上抵消了价格压力效应.

除了上述的两种效应之外,由增持效应, 情绪投资者的持有量减少, 导致风险降低, 进一步提升了股价. 此外, 情绪投资者往往不能准确把握市场时机(高买低卖), 随着情绪投资者的情绪放大,由这种错误的交易时机所导致的投资损失越严重. DeLong等[11]用Friedman效应描述了由于这种变化引发更高的市场风险, 从而降低收益率,使股价上升的现象. 综上所述, 以上三种效应的协同作用抵消了价格压力效应, 导致随着投资者悲观情绪的增加股价上升.

3.2其它参数分析

下文分析均衡时截面股价波动率等其它参数受投资者情绪的影响. 图3分析了股价波动率的变化, 参数选择与图1相同. 图中三条曲线对应的股利波动率分别为15%、 25%和35%.

图3　投资者情绪对均衡时股价波动率的影响

由图3可以看出本文的结论与经典文献的结论一致, 即投资者情绪的变化与市场波动性负相关. 但是三条曲线的斜率不同,这就意味着当标的资产本身的风险不一致时, 投资者情绪对于价格的波动影响不尽相同. 如图3所示,15%所对应的曲线斜率最高,这表明当标的资产风险更小时, 投资者乐观情绪对于股价波动率降低的作用越明显.

图4分析两类投资者财富之比对均衡时股价漂移率的影响, 参数选取如下: σδ=15%,Ω(t)=0.7,r=10%. 可以看出,随着变量η(t)的减小(即情绪投资者的财富比重增加),投资者情绪对于均衡时股价漂移率的影响越来越显著,这显然符合本文的预期: 当情绪投资者财富比重增加时,其实力增大,对于市场的影响力也随之增大,因此情绪投资者的投资情绪引发的股价变动也越大.

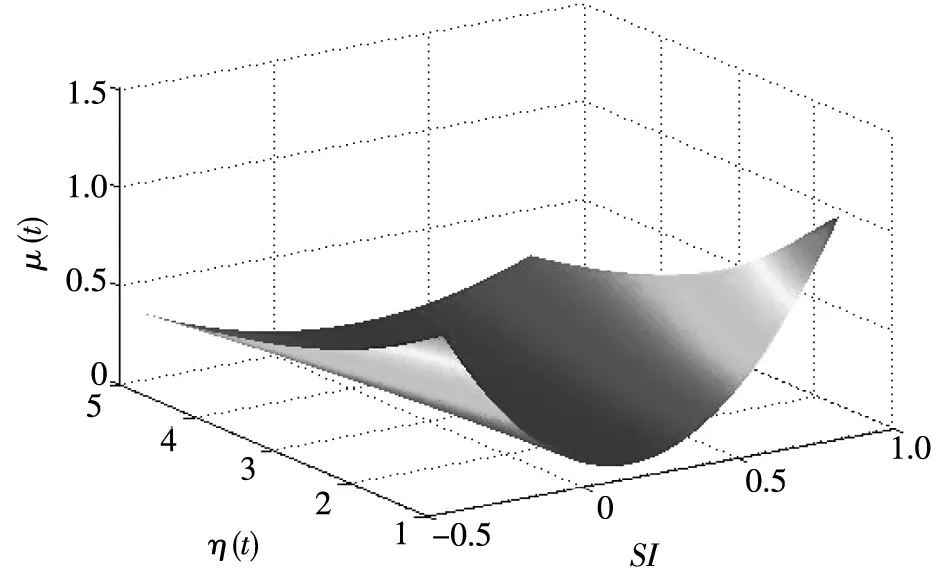
图4　两类投资者财富之比对均衡时股价漂移率的影响

图5　两类投资者风险贴现因子相对大小对均衡时股价漂移率的影响

在本文的假定中设置了ρ1<ρ2,这一假定事实上描述了两类投资者对于未来的重视程度. 同时在上文中看到变量Ω(t)正是取决于两者的风险因子大小的相对关系. 图5中其它参数与图1保持一致,从数值结果可以看出当Ω(t)减小时,理性投资者越发重视未来的收益,他们会更多地考虑情绪投资者的错误定价,以期从中获得投资收益.因此在这种情况下,均衡时股价漂移率将会更高.

4　结束语

已有行为金融的相关文献在投资者情绪方面做出了许多卓有成效的努力,本文的工作是对现有成果进行有益的延伸与拓展.本文将离散时间投资者情绪模型拓展到连续时间框架, 在异质投资者假设之下,利用Basak[16]的异质均衡求解方法, 在对数效用函数等假设下解得均衡时股价表达式. 研究结果表明,投资者情绪对于均衡时股价漂移率及波动率有显著的影响, 这意味着投资者情绪是影响收益的一个系统性因子. 乐观(悲观)的情绪变动将会使股价波动率降低(升高). 同时, 当情绪投资者的乐观情绪上升时,股票截面收益率上升, 这与经典文献结论一致; 当投资者的悲观情绪上升时,股票截面收益率也将上升,这是本文得到的新结果,可依照DeLong等[11]的框架, 从Friedman效应、理性投资者风险资产持有量等方面予以解释. 研究结果意味着情绪投资者关于股利信息的错误预期将会最终导致股价漂移率的上涨.

[1]LeRoy S, Richard P. The present-value relation: Tests based on implied variance bounds[J]. Econometrica, 1981, 49: 555-574.

[2]Mehra R, Edward P. The equity premium: A puzzle[J]. Journal of Monetary Economics, 1985, 15: 145-161.

[3]Barberis N, Greenwood R, Jin L, et al. X-CAPM: An extrapolative capital asset pricing model[J]. Journal of Financial Economics, 2015, 115(1): 1-24.

[4]郑敏. 异质信念、生存条件及市场影响力[J]. 管理科学学报, 2015, 18(8): 73-82.

Zheng Min. Heterogeneous beliefs, survival and market impact[J]. Journal of Management Sciences in China, 2015, 18(8): 73-82. (in Chinese)

[5]熊和平. 消费习惯、异质偏好与动态资产定价: 纯交换经济情形[J]. 经济研究, 2005, 10: 91-99.

Xiong Heping. Habit formation, heterogeneous preferences and the dynamics of asset prices: Pure exchange economy case[J]. Economic Research Journal, 2005, 10: 91-99. (in Chinese)

[6]熊和平, 李淑懿, 余均. 消费习惯、异质偏好与资产定价[J]. 管理科学学报, 2012, 15(9): 64-73.

Xiong Heping, Li Shuyi, Yu Jun. Habits formation, heterogeneous preferences and asset pricing[J]. Journal of Management Sciences in China, 2012, 15(9): 64-73. (in Chinese)

[7]Harrison J, Kreps D. Speculative investor behavior in a stock market with heterogeneous expectations[J]. Quarterly Journal of Economics, 1978, 92: 323-336.

[8]Varian H. Divergence of opinionin complete markets: A note[J]. The Journal of Finance, 1985, 40: 309-317.

[9]Varian H. Differences of opinion in financial markets[C]// in Courtenay C. Stone (ed.), Financial risk: Theory, Evidence and Implications. Proceedings of the Eleventh Annual Economic Policy Conference of the Federal Reserve Bank of St. Louis, Boston: Kluwer Academic Publishers, 1989, 3-37.

[10]Abel A. Asset prices under heterogeneous beliefs: Implications for the equity premium[R]. Working Paper. Philadelphia, University of Pennsylvania; P, 1989.

[11]DeLong J, Shleifer A, Summers L, et al. Noise trader risk in financial markets[J]. Journal of Political Economy, 1990, 98(4): 703-738.

[12]Williams J. Capital asset prices with heterogeneous beliefs[J]. Journal of Financial Economics, 1977, 5: 219-239.

[13]Wang J. A model of competitive stock trading volume[J]. Journal of Political Economy, 1994, 102: 127-168.

[14]Zapatero F. Effects of financial innovation on market volatility when beliefs are heterogeneous[J]. Journal of Economic Dynamics and Control, 1998, 22: 597-626.

[15]Basak S, Cuoco D. An equilibrium model with restricted stock market participation[J]. Review of Financial Studies, 1998, 11: 309-341.

[16]Basak S. Asset pricing with heterogeneous beliefs[J]. Journal of Bankingand Finance, 2005, 29(11): 2849-2881.

[17]Li T. Heterogeneous beliefs asset prices and volatility in a pure exchange economy[J]. Journal of Economic Dynamics and Control, 2007, 31(5): 1697-1727.

[18]Yang C, Zhang R. Dynamic asset pricing model with heterogeneous sentiments[J]. Economic Modelling, 2013, 33: 248-253.

[19]李维安, 李滨. 机构投资者介入公司治理效果的实证研究[J]. 南开管理评论, 2008, 6: 4-14.

Li Weian, Li Bin. An empirical study on the effect of institutional investors participating in corporate governance: Based on the data of 2004-2006 CCGI[J]. Nankai Business Review, 2008, 6: 4-14.(in Chinese)

[20]袁宁, 施嘉岳. 异质性时间偏好与资产定价[J]. 管理科学学报, 2012, 15(8): 50-59.

Yuan Ning, Shi Jiayue. Heterogeneous time preference and asset pricing[J]. Journal of Management Sciences in China, 2012, 15(8): 50-59.(in Chinese)

[21]Cox J, Huang C F. Optimal consumption and portfolio policies when asset prices follow a diffusion process[J]. Journal of Economic Theory, 1989, 49: 33-83.

[22]Rubinstein M. An aggregation theorem for securities markets[J]. Journal of Financial Economics, 1974, 1: 225-244.

[23]Karatzas I, Lehoczky J P, Shreve S E. Optimal portfolio and consumption decisions for a small investor on a finite horizon[J]. SIAM Journal of Control and Optimization, 1987: 1557-1586.

[24]张强, 杨淑娥. 噪音交易、投资者情绪波动与股票收益[J]. 系统工程理论与实践, 2009, 3: 40-47.

Zhang Qiang, Yang Shue. Noise trading, investor sentiment volatility and stock returns[J]. Systems Engineering: Theory & Practice, 2009, 3: 40-47.(in Chinese)

[25]Lee W Y, Jiang C X, Indro D C. Stock market volatility excess returns and the role of investor sentiment[J]. Journal of Bankingand Finance, 2002, 26(12): 2277-2299.

[26]王美今, 孙建军. 中国股市收益,收益波动与投资者情绪[J]. 经济研究, 2004, 10: 75-83.

Wang Meijin, Sun Jianjun. Stock market returns, volatility and the role of investor sentiment in China[J]. Economic Research Journal, 2004, 10: 75-83. (in Chinese)

[27]Bakshi G S, Chen Z. The spirit of capitalism and stock-market prices[J]. The American Economic Review, 1996, 86(1): 133-157.

[28]Campbell J Y, Cochrane H. By force of habit: A consumption-based explanation of aggregate stock market behavior[J]. Journal of Political Economy, 1999, 107: 205-251.

[29]Galí J. Keeping up with the Joneses: Consumption externalities, portfolio choice, and asset prices[J]. Journal of Money Credit and Banking, 1994, 26(1): 1-8.

[30]Barberis N, Huang M, Santos T. Prospect theory and asset prices[J]. Quarterly Journal of Economics, 2001, 116(1): 1-53.

[31]Constantinides G M, Donaldson J B, Mehra R. Junior can’t borrow: A new perspective on the equity premium puzzle[J]. The Quarterly Journal of Economics, 2002, 117(1): 269-296.

[32]Chan Y L, Kogan L. Heterogeneous preferences and the dynamics of asset prices[J]. Journal of Political Economy, 2002, 110(6): 1255-1285.

[33]Campbell J Y. Asset pricing at the millennium[J]. Journal of Finance, 2000, 55(2): 1515-1567.

[34]Shefrin H, Statman M. Behavioral capital asset pricing theory[J]. Journal of Financial & Quantitative Analysis, 1994, 29(3): 323-349.

[35]Barberis N, Shleifer A, Vishny R. A model of investor sentiment[J]. Journal of Finance, 1998, 49: 307-345.

[36]Daniel K, Hirsheifer D, Subramanyam A. Investor psychology and security market under and overreaction[J]. Journal of Finance, 1989, 53: 1839-1885.

[37]Hong H, Stein J C. A unified theory of underreaction, momentum trading and overreaction in asset markets[J]. Journal of Finance, 1999, 54(6): 2143-2184.

[38]张维, 刘文财, 王文启. 面向资本市场复杂性建模: 基于Agent计算实验金融理论[J]. 现代财经, 2003, 23(1): 3-8.

Zhang Wei, Liu Wencai, Wang Wenqi. The modeling for the complexity of capital market: Agent-based computationalexperiment financial[J]. Modern Finance and Economics, 2003, 23(1): 3-8. (in Chinese)

附录：

表1　行为资产定价模型文献总结

引理1的证明在本文中, 中央计划者的边际效用函数表示为

(36)

每一类投资者的效用函数的反函数表示为

(37)

参照Basak[16]性质1的证明, 结合正文部分推导, 引理得证.

证毕.

(38)

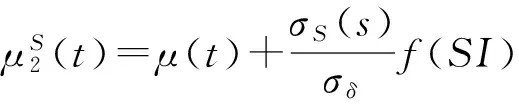
(39)

对上式进行因式分解

(40)

显然μ(t)≠r,所以均衡时漂移率可以表示为

(41)

其中 A(t)=(1-Ω(t))η(t)/σδ(1+η(t))(1+Ω(t)η(t)).

根据投资者的预算约束

Ci(t)]dt+πi(t)σS(t)Wi(t)dZi(t)

(42)

由于均衡时理性投资者的预期股价动态过程为

W1(t)θ1(t)dZ1(t)

(43)

联立两式可得

(44)

将各变量表达式代入,定理得证.

证毕.

Dynamic sentiment asset pricing with heterogeneous investors

ZENGYan1,KANGJun-qing1,CHENShu-min2*

1. Lingnan (University) College, Sun Yat-Sen University, Guangzhou 510275, China;2. School of Management, Guangdong University of Technology, Guangzhou 510520, China

This paper extends the discrete time sentiment asset pricing model to the continuous time setting using the consumption based pricing model. By incorporating heterogeneity in Lucas’s pure exchange economy, a dynamic sentiment asset pricing model for heterogeneous investors is established, and a central planning problem is studied. The investors’subjective drift rate of the stock price is derived by considering the sentiment factors, and then used in a dynamic asset pricing problem for heterogeneous investors to portray the differences between rational investors and sentiment investors.Contrary to the conventional wisdom that equilibrium stock price is not affected by investors’sentiment, this paper finds that investors’sentiment has a significant impact on the equilibrium stock price. Numerical examples and sensitivity analyses show that false expectation will lead to an increase in the drift rate of the stock price.

behavioral finance; heterogeneous pricing; sentiment pricing model

① 2015-03-26;

2015-12-20.

国家自然科学基金资助项目 (71571195; 71201173; 71301031); 霍英东教育基金会高等院校青年教师基金资助项目 (151081); 广东省自然科学杰出青年基金资助项目 (2015A030306040); 广东省自然科学基金研究团队资助项目(2014A030312003); 广东省科技计划项目(2016A070705024).本文入选“第十二届金融系统工程与风险管理年会”优秀论文(山西大学， 2014年8月).

陈树敏 (1979—), 男, 广东潮州人, 博士, 讲师. Email: chenshumin1@gmail.com

F224; F830

A

1007-9807(2016)06-0087-11