跳跃风险如何影响期权复制收益?①——基于多维跳跃扩散的模型与证据

刘杨树 , 郑振龙, 陈　蓉

(1. 厦门大学管理学院财务学系， 厦门 361005; 2. 厦门大学经济学院金融系, 厦门 361005)



跳跃风险如何影响期权复制收益?①
——基于多维跳跃扩散的模型与证据

刘杨树1, 郑振龙2, 陈蓉2

(1. 厦门大学管理学院财务学系， 厦门 361005; 2. 厦门大学经济学院金融系, 厦门 361005)

文章在最一般的多维跳跃扩散过程假设下，推导出Delta对冲组合盈亏所遵循的随机过程，从理论上证明了Delta对冲组合会受到跳跃风险以及跳跃风险的风险溢酬的影响.并且，通过美国SPX期权数据对理论推导的结论进行分样本实证，实证结果表明，在考虑了模型风险、市场信息传递效率等以往学者未曾考虑到的控制变量后，跳跃风险对于对冲标的风险后的期权复制收益的影响仍然显著，但其影响看涨看跌期权的内在途径和机理在平时、危机时刻都不相同.

跳跃扩散过程； 期权复制收益； 跳跃风险； 跳跃风险溢酬

0　引　言

大量研究表明，影响期权价格的风险源有许多[1-3].其中，跳跃风险是最重要的影响因素之一[4,5]，其原因可以归纳为三个方面：第一，跳跃风险是偶然发生的价格大幅变动，它与扩散(diffusion)风险这种连续发生的价格小幅变动有着本质的不同.相对于市场的小幅波动而言，投资者更厌恶跳跃风险.Pan[4]的研究表明，在美国期权市场上，跳跃导致的价格波动在总波动率中占比不到3%，但跳跃的风险溢酬达到了3.5%；相比之下，占总波动率超过97%的连续波动部分的风险溢酬仅为5.5%，这个结果引发了之后学者对期权中跳跃风险和跳跃风险溢酬研究的兴趣.第二，部分投资者(比如，套利者)会对期权中的标的资产风险进行对冲，但跳跃风险的存在使得这部分投资者无法完全对冲期权中标的资产的风险，此时，期权不再是标的资产的冗余证券，期权价格也将反映出投资者对跳跃风险敞口的态度.金融危机出现时，投资者对于期权中跳跃风险的敞口尤为厌恶，Santa-Clara和Yan[5]以及Broadie, Chernov和Johannes[6]的研究表明在危机时刻几乎所有的超额收益都是对于跳跃风险所要求的补偿.第三，期权中所隐含跳跃风险的信息还具有很强的预测性.比如，Yan[7]发现在美国金融市场上，期权中隐含的预期跳跃均值对个股的横截面收益具有明显的预测能力.总之，以往的研究都表明期权价格中隐含了大量跳跃风险的信息，而这些信息正是投资者的风险态度中最敏感的部分.由于我国目前期权交易量还较小，因此，虽然部分国内学者已经关注市场上跳跃特征[8-10]或风险溢酬[11, 12]，但对期权中隐含跳跃风险信息的研究还比较少.

在当前中国市场上，上海证券交易已经推出了上证50ETF期权，市场上做市商面临的标的资产扩散风险可以被Delta对冲策略所对冲，而剩余的风险则来自标的资产的跳跃.未来中国必然推出更多的期权，在这一背景下，极端的跳跃风险将如何对Delta对冲后的组合产生影响，这不仅是做市商们需要关注的问题，也是监管层所应考虑的问题.本文写作的目的在于探寻Delta对冲组合背后残留的风险，尤其是跳跃风险所带来的影响.

本文的主要工作如下：首先，本文在一般化的多维跳跃扩散过程下，推导出Delta对冲组合(也可以看成Delta对冲策略下的期权复制收益)中所包含的风险和信息.从理论上证明了所有状态变量的跳跃风险以及跳跃风险的风险溢酬都可能对期权的Delta复制收益产生影响；此外，除了标的资产的风险溢酬，其他所有状态变量扩散风险的风险溢酬也可能会对期权的Delta复制收益产生影响*推导的结果仅表明跳跃对于Delta对冲组合可能产生影响，但其参数是否显著，符号正负都不确定，因此，需要实证来验证各个部分的参数是否显著..其次，在实证中，本文借鉴以往的研究构建了跳跃风险的代理变量，并通过美国市场的期权数据进行检验.本文验证了理论推导公式中的部分参数在现实中的确是显著的，并且进行了分样本的稳健性检验，发现跳跃风险对看涨期权和看跌期权的Delta对冲组合影响是不同的.最后，本文进一步考虑了平时和危机时期期权中隐含跳跃风险的差异，并对相应的实证结果作出评述.

与以往的文献相比，本文的贡献主要体现在三个方面：第一，本文首次在一个一般化的多维跳跃扩散过程假设下，推导出Delta对冲组合盈亏(即Delta对冲策略下的期权复制收益)的随机形式；第二，本文的实证研究表明，跳跃风险对于期权复制收益的影响途径十分复杂，在不同时期对于不同期权跳跃风险的影响是不一样的，这是以往学者并未注意到的；第三，在实证中，本文首次在类似的研究中将模型风险以及信息传递效率作为控制变量，并发现它们能够在一定程度上显著地影响Delta对冲组合的收益.

1　多维跳跃扩散模型下的期权复制

收益

讨论在一般化的假设下，跳跃风险将如何影响Delta对冲组合的收益*为了与以往的研究具有可比性，本文的Delta对冲组合也是由一单位期权多头和Δ单位标的资产空头构成的..假设标的资产价格和影响期权价格的其他状态变量均服从最一般的跳跃扩散过程[13]

(1)

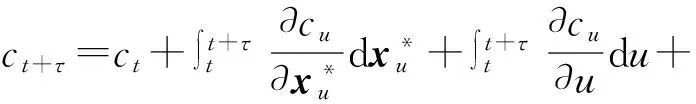
(2)

当状态变量服从式(1)时，根据Girsanov定理，在风险中性世界中，衍生品价格必须满足偏微分方程，整理可得

(3)

(4)

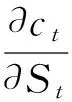
(5)

可以看出，Πτ由三部分构成：期权多头价值的变化；动态调整的标的资产空头价值的变化；因标的资产数量的动态调整而产生的融资需求的变化.若标的资产可以完美地复制期权，那么Πτ应等于0.

此外，还必须假设标的资产St在现实世界与风险中性世界所服从的过程

(6)

(7)

上两式里标的资产所对应的参数都用上标S标记.将式(4)和式(7)代入式(5)，可得

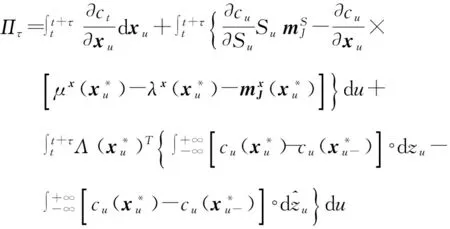
(8)

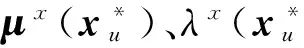
(9)

式(9)意味着Delta对冲后，剩余组合的收益取决于五个部分：第一部分是期权对标的资产之外其他状态变量的一阶偏导与其相应扩散风险风险溢酬的乘积；第二部分代表Delta对冲组合受其他状态变量的扩散风险影响造成的波动；第三部分代表Delta对冲组合受其他状态变量的跳跃的影响；第四部分是跳跃过程的补偿项；第五部分即为跳跃风险溢酬.其中，第二部分和第三部分是随机的.当时间间隔τ极短时，式(9)的期望可以写成

(10)

式(10)表明一般化的Delta对冲组合的期望收益受四个因素影响：第一，受标的外其他状态变量扩散风险溢酬的影响；第二，受其他状态变量极短时间内跳跃幅度期望值总和的影响；第三，受标的资产跳跃的平均期望的影响；第四，受所有状态变量跳跃风险溢酬影响.这意味着，理论上看，即使期权投资者(无论多空)对冲了标的资产，其头寸仍可能受到标的和其他状态变量跳跃的影响.但理论推导并不保证式(10)中的参数在现实中的显著性.因此，下文将Delta对冲收益设为因变量，寻找式(10)中的各种状态变量的风险溢酬的代理变量进行实证研究，回归系数的显著性能够说明式(10)中系数的显著性*Bakshi和Kapadia[3]用式(10)的一个特殊形式来检验波动率风险溢酬的..

2　实证设计

第一部分从理论上表明：在多维跳跃扩散模型下，跳跃风险是影响Delta对冲收益的重要因素之一.当代表跳跃风险溢酬或跳跃幅度的参数显著时，跳跃对Delta对冲策略结果的影响无法忽略.但这些参数的显著性要用实际市场数据一一检验.具体而言，在式(10)的基础上，通过检验Delta对冲收益和跳跃风险之间关系的显著性，可以表明跳跃风险能否在对冲时被忽略.

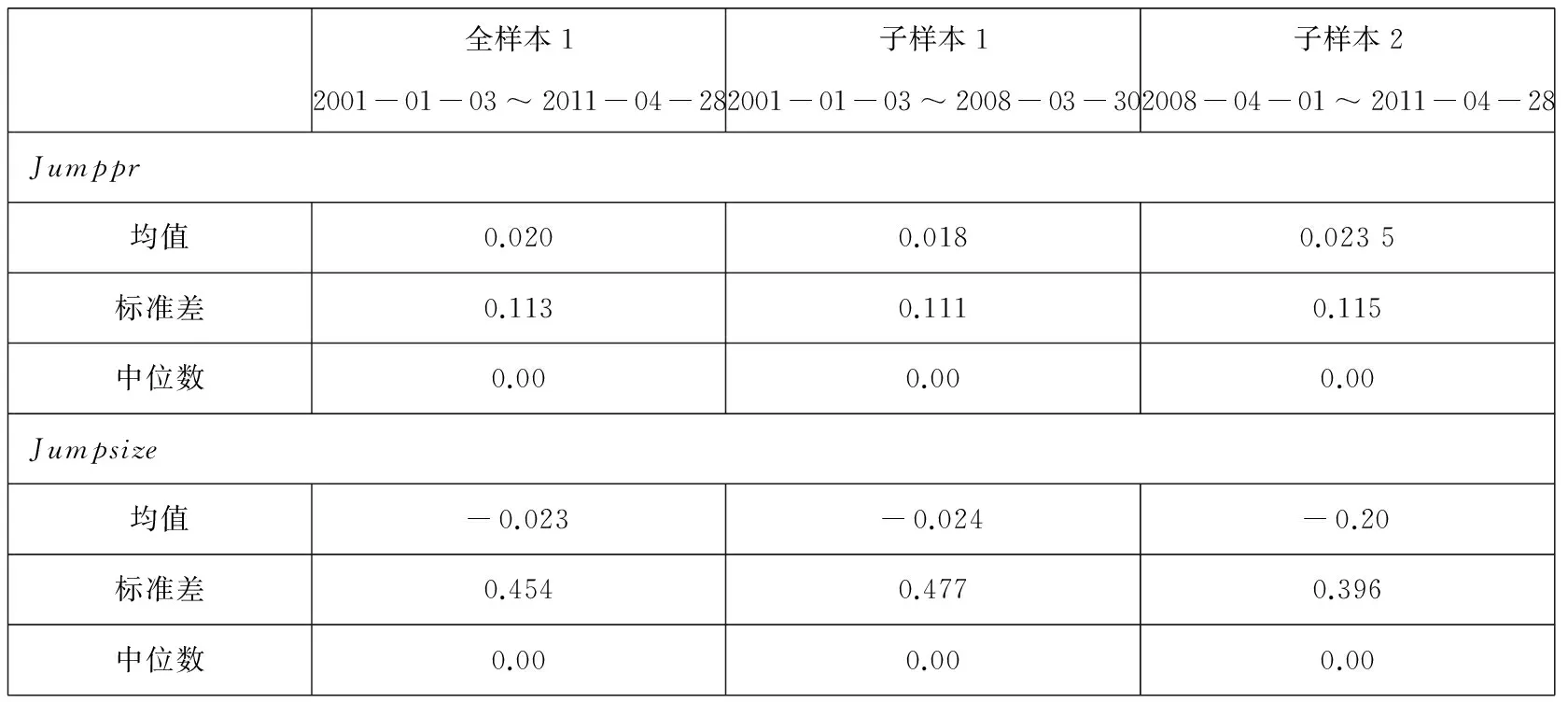
2.1实证数据与样本筛选

实证研究的样本从2001年1月3日至2011年4月28日的美国SPX指数看涨期权、看跌期权及其标的资产(美国S&P500指数)的日数据*因此，下文中的衍生品即为股指期权，标的资产则为S&P500股价指数，Delta对冲组合由股指期权和股票指数组成.，数据来自www.ivolatility.com.选择这个样本期的原因在于，这段期间包含了互联网泡沫崩溃期和次贷危机，对跳跃风险的分析具有较大的意义.

借鉴Jackwerth和Rubinstein[14]、Buraschi和Jackwerth[15]以及Bakshi和Kapadia[3]的方法，样本数据的筛选标准如下：1)看涨期权价格应处于上下限[St-K,St]之间，看跌期权价格应处于[K-St,K]之间*其中K代表期权合约的执行价格.，此条件保证所采用的期权价格应不违背最基本的无套利原则，属于合理价格；2)由于期限太长和太短的期权交易都很不活跃，因此本文借鉴Bakshi和Kapadia[3]剔除剩余期限太长和太短的数据，采用剩余期限在14天到60天之间的期权数据；3)深度实值和深度虚值期权的市场流动性不佳，且价格中带有大量的市场微观结构噪音，因此本文采用接近平价的期权*Yan[7]表明Delta绝对值为0.5的平价期权中也能包含跳跃的信息.，具体标准为ln(S/K)∈[0.951.05]；4)同样出于流动性的考虑，最后还剔除了日交易量小于500手的期权，以保证期权价格的合理性.

经过筛选之后，本文所使用的期权样本数据是一个面板数据，共包括2 482天，每天平均有8.29个期权的数据，最多一天有57个期权数据，最少一天有0个期权数据*由于期权复制收益的计算需要有同一个期权前后两天期权交易数据，因此部分天数没有Delta对冲收益，所有期权的平均剩余期限为0.091年(一个月左右)，期权每天的平均交易量为4 629手，平均的隐含波动率为18.73%.SPX期权的标的资产——S&P500指数则是一个2 482天的时间序列数据.

一般认为，2008年3月的贝尔斯登事件是次贷危机爆发的标志性事件.为了控制次贷危机的影响，更全面地考察跳跃风险和跳跃风险溢酬问题，本文除了进行全样本分析，在稳健性检验中进一步将样本分为子样本1(2008年3月以前)与子样本2(2008年3月之后)进行分析，以得到更为详细和全面的结论.需要说明的是，本文中所用的无风险利率采用欧洲美元的隔夜拆借利率，数据来自Bloomberg.在后续的变量设定中，有时还需要一些其他的数据作为补充，将在下文介绍变量设定时具体解释.

2.2实证模型与变量的说明

与理论模型(10)对应，本文将通过包络回归验证不同变量对于期权复制收益的影响，回归式子如下

(11)

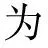
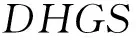
其中T-t是期权剩余期限，τ是两个交易日间的时间长度(以年为单位)*针对样本内的每个期权，在每两个交易日之间，计算相应的DHGS值，将其作为一个观测值..表1报告了分别针对整个样本和子样本计算得到的因变量DHGS的基本信息.从表1中，可以看出，首先，次贷危机爆发后Delta对冲收益的标准差比危机前要高，这显然是符合直觉的：在次贷危机爆发后，市场的大幅波动必然导致Delta对冲收益的不稳定性；其次，次贷危机爆发后期权多头所对应的Delta对冲收益所获得的收益率也较大，这可能是由于危机后，Gamma效应较大(因为市场波动率上升)的缘故.

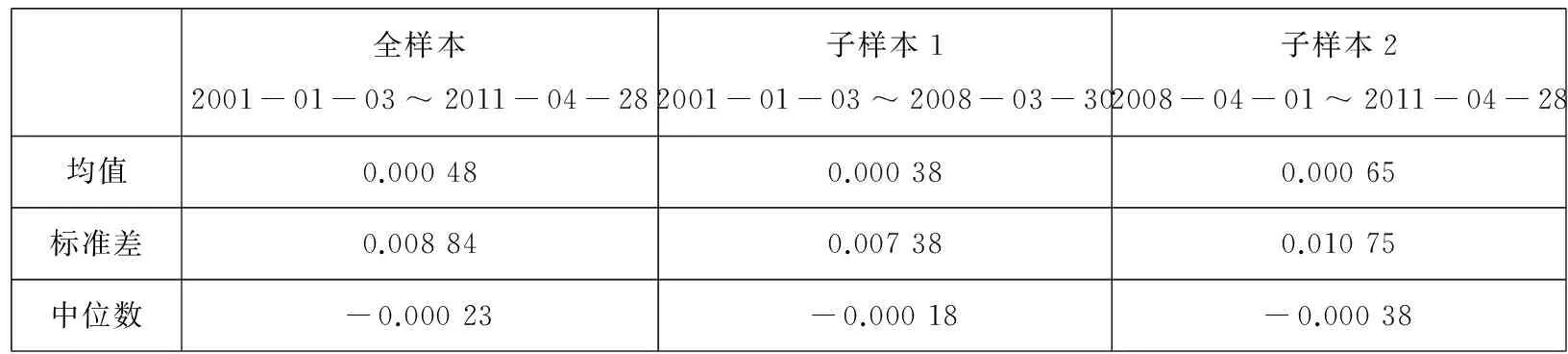
表1　因变量DHGS的描述性统计

2.2.2跳跃因子的构造

构造跳跃因子的步骤如下：首先要侦测出市场是否存在跳跃；其次，基于侦测的结果计算每次跳跃发生的概率以及跳跃的大小；最后，将跳跃发生的概率和跳跃的大小作为跳跃因子，具体过程如下：

1)跳跃的侦测：常见的跳跃因子侦测方法包括Barndorff-Nielsen和Shephard[17]、Jiang和Oomen[18]以及Lee和Mykland[16].本文对于期权的标的资产跳跃的侦测是建立在Lee和Mykland[16]的非参数侦测方法基础上的，具体构造方法如下，首先计算出

(12)

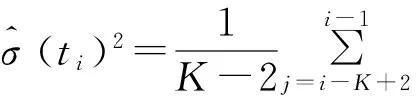
其中n是每年的观测数，选择n=252天

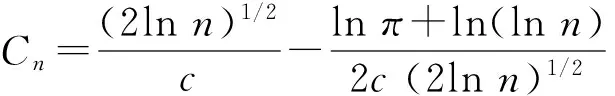
根据Lee和Mykland[16]，当

时，则在10%的显著水平下拒绝原假设(市场不发生跳跃).

2)跳跃概率因子

从Lee和Mykland[16]的侦测过程中，不难看出ξ的值实际上反映了拒绝原假设的显著水平，因此，ξ的值越大，则依据Lee和Mykland[16]，其发生跳跃的概率就越大.本文将这个置信水平作为跳跃发生概率的代理变量，即

Jumpprt=exp(-e-ξ)

(13)

3)跳跃大小因子

跳跃大小因子计算的是在发生跳跃的时候，跳跃幅度的大小.首先，根据Lee和Mykland[16]的方法，将10%的显著水平上发生跳跃的交易日标记为1，没有发生跳跃的交易日标记为0，即

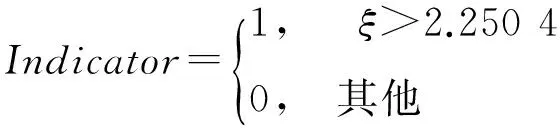
(14)

其次，本文用Lee和Mykland[16]的L作为跳跃大小的代理.L衡量的是经过近期波动率标准化后的日收益率，因此跳跃幅度大小的因子如下

Jumpsizet=Indicatort×L(t)

(15)

其他5个控制变量选取的具体理由和因子构造方法如下.

2.2.3波动率因子(Vega)

由于Bakshi和Kapadia[3]已经发现，基于BS模型构造的Delta对冲组合盈亏中含有非常显著的波动率风险溢酬，因此必须控制Delta对冲组合中波动率风险因子的影响.参照Bakshi和Kapadia[3]，对于期权来说，衡量其波动率风险暴露的最好指标就是Vega，即期权价格对波动率的一阶偏导.鉴于此，本文采用BS模型计算出的Vega作为实证方程中波动率风险因子的代理变量.

2.2.4模型设定偏误因子(Model)

无论何种模型都存在模型设定偏误的可能，因此，研究者总会遇到类似Roll批评的困境，在本文的环境中即为：无法判断参数的显著性是由于模型的不精确，还是由于跳跃风险的确为系统性风险所致.为控制模型设定偏误的影响，作者通过一个简单而又有效的方法来打破联合检验的困境，其思想来自于郑振龙和刘杨树[19]的研究.其经济含义如下：在Delta对冲策略中，当对冲所选用的头寸由于模型设定有误而发生误差时，Delta对冲组合的盈亏仍将受到标的资产价格在现实世界中漂移率的影响.因此在实证中，引入与计算DHGS时的τ期间对应的标的资产收益率作为控制模型设定偏误的变量.这个控制变量的加入有两个作用：第一，检验BS模型估计出的Delta是否合理.若不合理则控制变量的系数显著，反之则不显著.第二，剔除模型风险的影响.若BS模型存在较为严重的模型设定误差，则回归中标的资产收益率的系数就会是显著的，而这一项就可以剔除模型设定偏误的影响，从而保证跳跃风险以及跳跃风险溢酬估计的稳健性.

2.2.5信息传递效率差异因子(Efficiency)

在期权隐含风险的现有研究中，大部分学者都没有考虑期权市场的信息传递效率问题.但实际上，由于期权市场的高杠杆性质和低交易成本优势，期权价格对新信息的反应往往领先于标的资产价格.传统的定价模型并没有考虑信息传递效率问题，此时，Delta对冲组合是基于同一时刻的期权价格和股票价格构建的.这样，倘若短期内期权价格领先于股票价格且套利还未发生作用，研究Delta对冲组合的收益率就会导致对结果的误读.

基于此，本文引入代表信息传递效率的指标作为控制变量，以剔除Delta对冲组合盈亏中期权市场相对标的资产市场的高效率带来的影响.依据Garleanu, Pedersen和Poteshman[20]以及Cremers和Weinbaum[21]，本文用相同在值程度的看涨看跌期权的隐含波动率之差作为信息传递效率的代理变量.其原理很简单，如果期权市场满足无套利的看涨看跌平价(put-call parity，PCP)公式，相同在值程度的看涨看跌期权的隐含波动率之差应该为0；而当信息到来时，期权价格有可能因为短期内套利无法实现而偏离PCP公式.本文用每个交易日不同到期日、不同行权价、相同在值程度的看涨看跌期权的隐含波动率之差的加权和来构造当天的信息传递效率因子

(16)

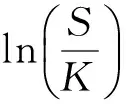
表3报告了这五个控制变量在全样本期间以及非危机和危机期间的描述性统计.

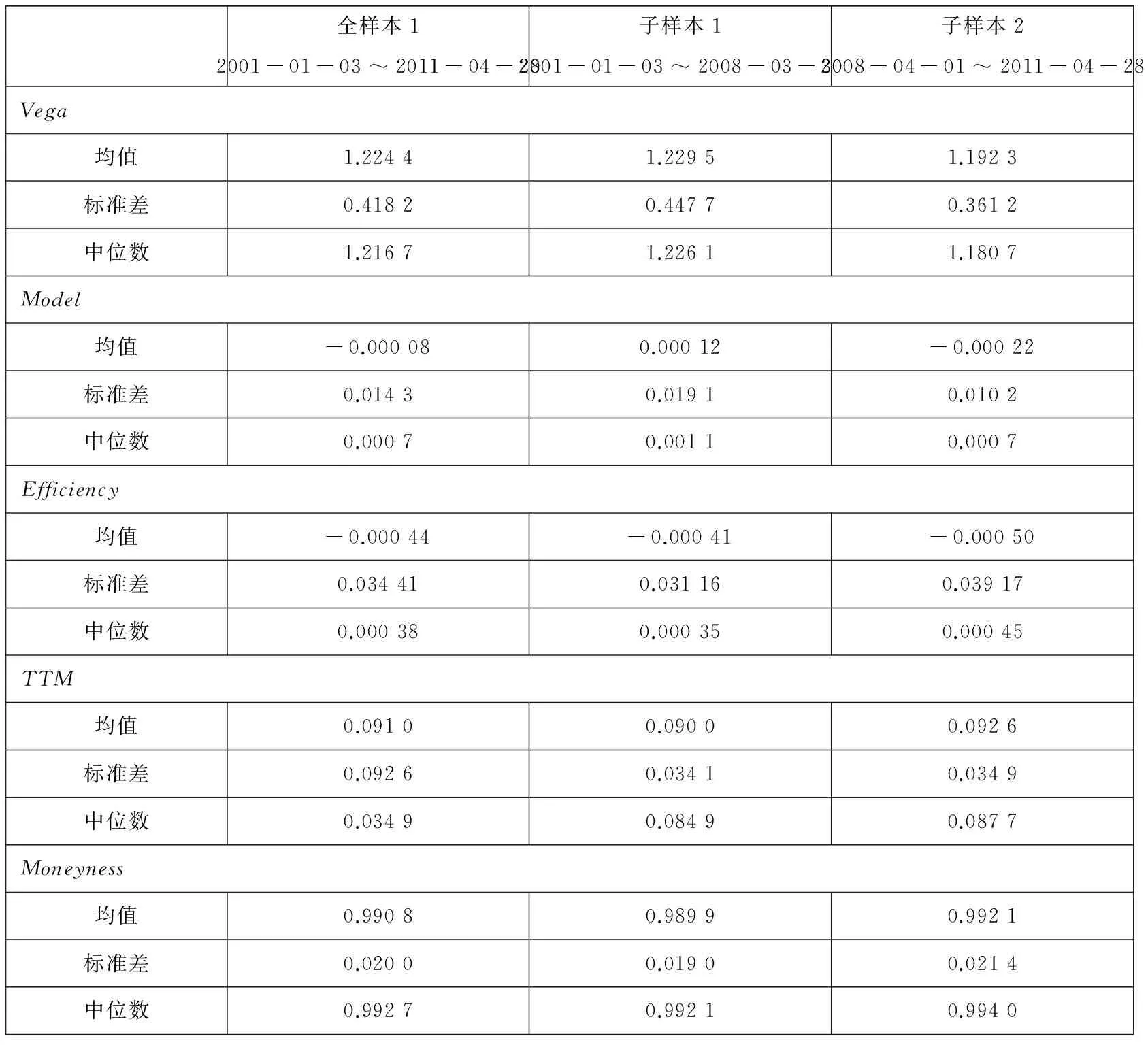
表3　控制变量的描述性统计

3　实证结果

本文最关注的自变量是跳跃的两个风险因子跳跃概率和跳跃大小的系数β1,β2，其是否显著能说明三个问题：第一，在建模时，是否需要考虑跳跃风险；第二，跳跃发生时，那些对冲标的风险的期权投资者所得到的盈亏的符号和大小；第三，从全市场角度看，是否存在跳跃风险溢酬.

表4与表5列出了全样本包络回归的结果，为了观察跳跃对看涨期权和看跌期权的影响，本文将看涨期权和看跌期权分开进行回归.

表4与表5的结果揭示了许多信息：

1)在表4对看涨期权的检验中，跳跃概率因子系数都显著，且为正.本文认为，此处跳跃概率因子代表了收益率超出近期正常波动的概率，因此，其系数显著为正可以通过期权的Gamma收益来解释，即标的资产的变动越大，即使经过线性对冲后，期权中隐含的非线性项仍然能够带来正收益.

2)对于看涨期权而言，跳跃大小因子的符号为负，且大多显著，即使系数不显著的模型5和模型6其显著性也接近10%.主要原因是跳跃方向大多为负向，因此，当市场上持有看涨期权的一方未能对这种负向的跳跃有足够预期时，发生负向跳跃就仍然会使得Delta对冲后的看涨期权持有者获得收益(跳跃大小大多为负，系数也为负，负负得正).综合前一点，这表明在看涨期权中跳跃的风险溢酬不仅存在，还分为跳跃概率的风险溢酬和跳跃大小的风险溢酬.

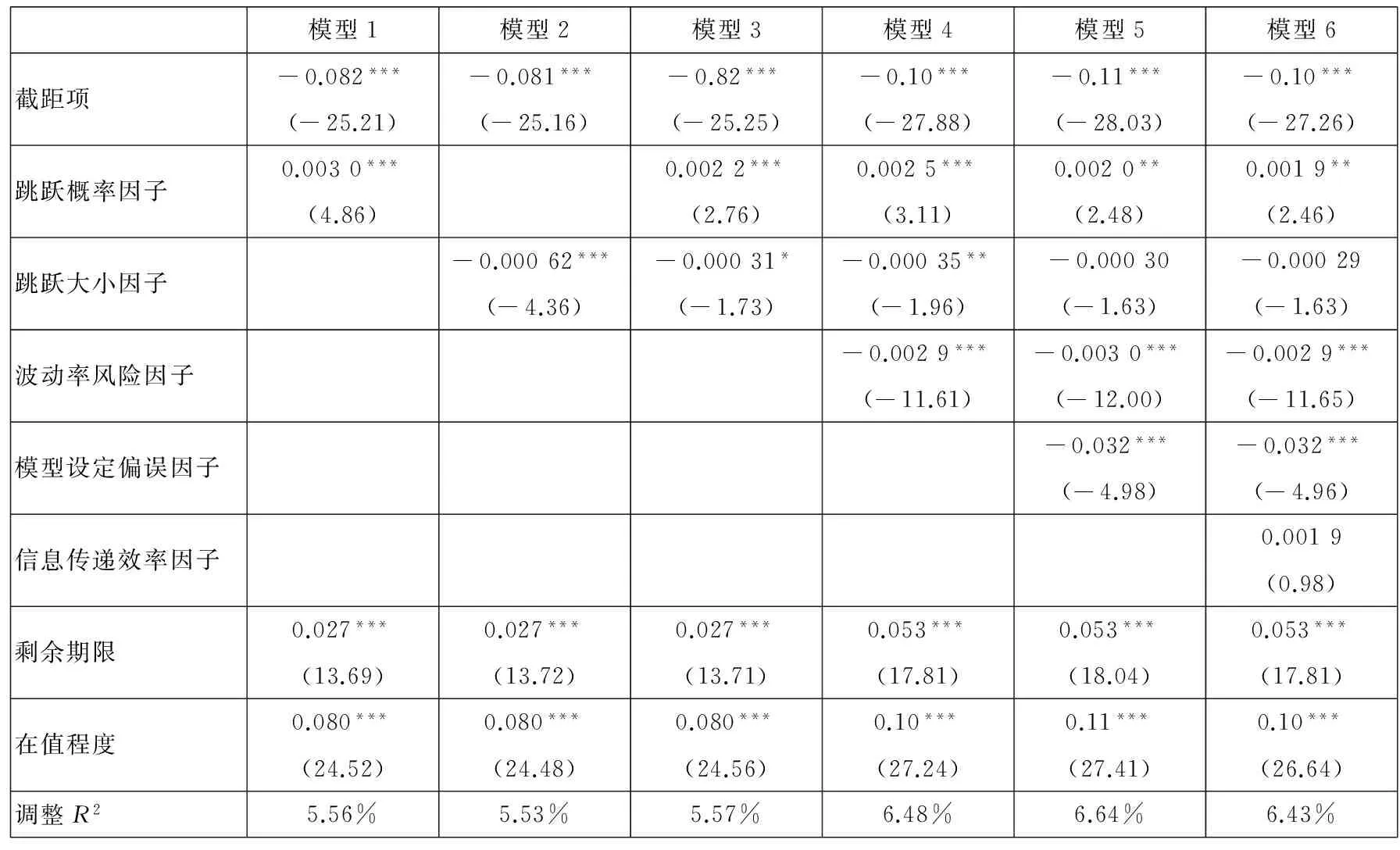
表4　全样本看涨期权的回归结果 (2001-01-03～2011-04-28)

表5　全样本看跌期权的回归结果(2001-01-03～2008-03-30)

3)在对看跌期权的检验中，发现看跌期权的跳跃概率因子以及跳跃大小因子均不显著，这是一个很有趣的现象.它表明了，看跌期权市场上的投资者实际上已经合理的预期到未来的跳跃概率和跳跃的大小，且平均而言购买看跌期权的投资者是风险中性的，不需要跳跃风险的补偿.因此，在对冲标的资产后看跌期权的盈亏在市场上真实发生跳跃时，并没有受到太大的影响.结合看涨期权的结论，认为看跌期权的投资者比看涨期权的投资者更加理性，因此，其价格反应更加灵敏.

4)在全样本中，波动率风险因子的影响总是显著为负的，其与跳跃因子之间的相互影响并不大，这意味着从总体上看，市场对于跳跃风险和波动率风险还是有所区分的.

5)在回归中，大部分控制变量的系数都是显著的，且这些系数的显著水平大部分都在1%以上.这表明，Delta对冲策略下的期权复制收益的确会受到波动率风险、模型设定偏误、信息传递效率、期权的到期时间和在值程度的影响.

4　稳健性检验

为了进一步检验跳跃风险的影响及其稳健性，在这部分本文将以贝尔斯登事件为分界点将样本分为2008年3月之前和2008年3月之后.首先，表6与表7报告了模型1、模型2和模型6的看涨期权与看跌期权在两个子样本的结果.

可以看到，在子样本回归中，因子的影响方向都并没有太大改变，但全样本的显著性却可以由两个子样本的不同表现来进一步分析.由两个样本来看，看涨期权的跳跃大小因子的显著性在子样本2中更为显著，而在子样本1中的显著性则不稳定.这意味着看涨期权的投资者在子样本2期间对于向下跳跃的预期不足，因此，向下跳跃给对冲后的看涨期权组合会带来意外的Gamma收益.而在看跌期权方面，无论在哪个样本都是不显著的，这表明，看跌期权的投资者更可能是机构投资者，其对于市场的判断能力在两个样本期是一致的.

结合全样本的结果，对应地总结出三点：第一，跳跃风险溢酬只存在于看涨期权之中，而几乎不存在于看跌期权之中.第二，从建模角度出发，看涨期权的复制收益受到跳跃的影响较大，其市场价格中含有跳跃风险溢酬，因此，研究跳跃风险溢酬更应该对看涨期权进行建模和实证；看跌期权的价格几乎不受已实现跳跃的影响，因此，预测跳跃风险时更应当对看跌期权价格进行建模和实证.第三，对于投资者而言，看涨期权投资者对冲标的资产后的收益会受到已实现跳跃的影响，而看跌期权的投资者对冲标的资产后的收益则不受已实现跳跃的影响.

表6　子样本1(非危机时段)实证结果(2001-01-03～2008-03-30)

5　结束语

本文的研究首先从理论推导出发，得出了期权复制收益在一般情况下的解析表达式，之后，依据该结论对美国股指期权中所隐含的跳跃风险和跳跃风险溢酬进行了深入的实证分析，结果发现：

第1，理论上说，跳跃风险的跳跃方向以及跳跃的风险溢酬都会对期权的复制收益的产生影响，因此，即使对冲了期权标的风险，标的资产的跳跃仍然可能给投资者的带来冲击.但跳跃风险溢酬最后是否显著，仍然取决于模型中的参数是否显著不为零，因此，跳跃风险溢酬最终的显著性取决于实证的结果，这也暗示着跳跃风险溢酬可能由于市场和期权种类的改变而有所不同.

第2，在进行实证研究时，本文发现在美国S&P指数期权上，跳跃的概率和跳跃的大小对于不同期权的影响是不同的.对于看涨期权而言，跳跃概率因子的系数为正，而对于跳跃大小因子而言，其系数为负；但对于看跌期权而言，跳跃概率因子和跳跃大小因子的系数都不显著.其背后原因极有可能是看涨期权和看跌期权的投资群体的差异所造成.

第3，美国股票市场上的跳跃风险溢酬主要呈现在看涨期权中，并且，已实现的跳跃，无论是跳跃的概率或是跳跃的大小给对冲后的看涨期权组合带来的都是正收益，因此，在为S&P的看涨期权建模时，必须充分考虑跳跃风险及其风险溢酬的存在性和时变性.另一方面，看跌期权不受已实现跳跃的影响意味着其投资者对于已实现跳跃的预期更为充分，因此，在研究期权信息的预测能力时，更应该使用看跌期权中的信息.

[1]Bakshi G, Cao C, Chen Z. Empirical performance of alternative option pricing models[J]. The Journal of Finance, 1997, 52: 2003-2050.

[2]Bates D S. Post-'87 crash fears in the S&P 500 futures option market[J]. Journal of Econometrics, 2000, 94(1-2): 181-238.

[3]Bakshi G, Kapadia N. Delta hedged gains and the negative market volatility risk premium[J]. Review of Financial Studies, 2003, 16(2): 527-566.

[4]Pan J. The jump-risk premia implicit in options: Evidence from an integrated time-series study[J] . Journal of Financial Economics, 2002, 63(1): 3-50.

[5]Santa-Clara P, Yan S. Crashes, volatility, and the equity premium: Lessons from S&P 500 options[J]. The Review of Economics and Statistics, 2010, 92(2): 435-451.

[6]Broadie M, Chernov M, Johannes M. Model specification and risk premia: Evidence from futures options[J]. The Journal of Finance, 2007, 62(3): 1453-1490.

[7]Yan S. Jump risk, stock returns, and slope of implied volatility smile[J]. Journal of Financial Economics, 2011, 99(1): 216-233.

[8]王春峰， 姚宁， 房振明, 等. 中国股市已实现波动率的跳跃行为研究[J]. 系统工程, 2008, 26(2): 1-6.

Wang Chunfeng, Yao Ning, Fang Zhenming, et al. An empirical research on jump behavior of realized volatility in Chinese stock markets[J]. System Engineering, 2008, 26(2): 1-6. (in Chinese)

[9]马成虎, 汪先珍. 中国股市价格的跳跃行为: 基于上证综指高频数据的参数分析[J]. 中国金融评论， 2009， (4): 31-66.

Ma Chenghu, Wang Xianzhen. The jump behavior of China’s stock market prices: An analysis with the high frequency data of the SSECI[J]. Chinese Review of Financial Studies, 2009, (4): 31-66. (in Chinese)

[10]陈浪南, 孙坚强. 股票市场资产收益的跳跃行为研究[J]. 经济研究, 2010, 45(4): 54-66.

Chen Langnan, Sun Jianqiang. Jump dynamics in stock returns[J]. Economic Research Journal, 2010, 45(4): 54-66. ( in Chinese)

[11]左浩苗, 刘振涛. 跳跃风险度量及其在风险—收益关系检验中的应用[J]. 金融研究, 2011， (10) : 170-184.

Zuo Haomiao, Liu Zhentao. Jump risk measurement and its application in the test of the relationship between risk and return[J]. Journal of Financial Research, 2011, (10): 170-184. (in Chinese)

[12]陈蓉， 方昆明. 波动率风险溢酬: 时变特征及影响因素[J]. 系统工程理论与实践， 2011， (4): 761-770.

Chen Rong, Fang Kunming. Volatility risk premium in Hong Kong stock market[J]. Systems Engineering: Theory & Practice, 2011, (4): 761-770. (in Chinese)

[13]Duffie D, Pan J, Singleton K. Transform analysis and asset pricing for affine jump diffusions[J]. Econometrica, 2000, 68(6): 1343-1376.

[14]Jackwerth J C, Rubinstein M. Recovering probability distributions from option prices[J]. The Journal of Finance, 1996, 51(5): 1611-1631.

[15]Buraschi A, Jackwerth J. The price of a smile: Hedging and spanning in option markets[J]. Review of Financial Studies, 2001, 14(2): 495-527.

[16]Lee S S, Mykland P A. Jumps in financial markets: A new nonparametric test and jump dynamics[J]. Review of Financial Studies, 2008, 21(6): 2535-2563.

[17]Barndorff-Nielsen O E, Shephard N. Econometrics of testing for jumps in financial economics using bipower variation[J]. Journal of Financial Econometrics， 2006, 4(1): 1-30.

[18]Jiang G J, Oomen R C A. Testing for jumps when asset prices are observed with noise[J]. Journal of Econometrics, 2008, 144(2): 352-370.

[19]郑振龙， 刘杨树. 衍生品定价: 模型风险及其影响[J]. 金融研究， 2010， (2): 112-131.

Zheng Zhenlong, Liu Yangshu. Model risk and its effects on pricing derivatives[J]. Journal of Financial Research, 2010, (2): 112-131. (in Chinese)

[20]Garleanu N, Pedersen L H, Poteshman A M. Demand-based option pricing[J]. Review of Financial Studies, 2009, 22(10): 4259-4299.

[21]Cremers M, Weinbaum D. Deviations from put-call parity and stock return predictability[J]. Journal of Financial and Quantitative Analysis, 2010, 45(2): 335-367.

How does jump risk affect the Delta hedge gain? Evidence from multi-dimension jump diffusion model

LIUYang-shu1,ZHENGZhen-long2,CHENRong2

1. Department of Finance, School of Management, Xiamen University, Xiamen 361005, China;2. Departmetn of Finance, School of Economics, Xiamen University, Xiamen 361005, China

This paper derives the stochastic process of Delta hedge gain under the general jump diffusion process. Theoretically, Delta hedge gain contains four components, including jump risk and risk premium of jump risk in our assumption. The theoretical result is tested with SPX option data. The empirical result indicates that complex roles jump affects option prices. The result is significant when the model risk and market efficiency effects are controlled. It is found that in different financial environments, different types of options are affected differently by the jumps.

jump diffusion process; Delta hedge gain; jump risk; risk premium of jump risk

① 2014-06-20；

2014-09-30.

国家自然科学基金资助青年项目(71101121； 71401144)； 国家自然科学基金资助项目(71073023)； 教育部人文社科研究青年基金资助项目(11YJC790014); 福建省自然科学基金项目(2010J0619).

刘杨树(1984—)， 男， 福建福州人， 博士， 助理教授. Email: ysliu@xmu.edu.cn

F832.5

A

1007-9807(2016)06-0074-13