分析师跟踪与股价同步性——基于过度反应视角的证据①

周铭山, 林　靖, 许年行

(1． 西南财经大学金融学院, 金融安全协同创新中心， 成都 611130； 2． 北京大学经济学院，北京 100871； 3． 中国人民大学商学院， 北京 100872)



分析师跟踪与股价同步性
——基于过度反应视角的证据①

周铭山1, 林靖2, 许年行3

(1． 西南财经大学金融学院, 金融安全协同创新中心， 成都 611130； 2． 北京大学经济学院，北京 100871； 3． 中国人民大学商学院， 北京 100872)

对我国股票市场分析师跟踪与股价同步性的关系进行研究，本文发现：(1)即使明星、非明星分析师提供相似的信息，明星分析师显著降低了R2(股价同步性)，而非明星分析师则不然；(2)明星分析师预测准确度最高组和最低组股票的平均R2并无显著差异；上述结果表明信息提供并不能完全解释我国明星分析师降低股价同步性的现象.(3)明星分析师跟踪及评级调整与短期动量效应、中长期反转效应以及异常成交额存在显著的正向关系，这一发现支持了本文的假说，即明星分析师通过引起投资者过度反应而降低股价同步性.本文的研究对于认识分析师在我国证券市场中的作用以及股价同步性的生成机理具有重要的理论与现实意义.

明星分析师； 过度反应； 股价同步性

0　引　言

股价同步性(即股票收益率市场模型中的R2)通常被用以衡量股价中所包含的公司层面信息的含量，较小的R2意味着股价波动在很大程度上由市场以外的公司层面因素引起，即股价中包含较多的公司层面信息.根据这一逻辑，Chan 等[1]认为，由于没有促进公司层面信息的传递，包含中国在内的新兴市场国家的分析师没能降低R2.考虑了分析师的异质性后*已有文献对分析师的异质性进行了考察，Stickel [4]的研究表明，相对于普通分析师，明星分析师(“全美分析师”，下同)所发布的盈余预测报告更加准确，其对股价的影响也更大；Fang 等[5]对投资评级报告进行的研究结果表明，明星分析师推荐的股票更具有投资价值.，Xu等[2]认为，我国的明星分析师因促进公司层面信息的传递而显著地降低了R2.

然而，越来越多的文献开始质疑股价同步性与公司层面信息的联系*这些文献包含但不限于Ashbaugh-Skaife等[6]、Teoh等[7]、Chang 等[8]、Hou等[3]，等等.，在这些文献中， Hou 等[3]发现，当投资者对公司层面信息的反应是无偏的，越多的公司层面信息导致更低的当期R2；但当投资者对公司信息存在认知偏差时，特别是，当市场存在长期过度反应时，R2则与市场过度反应呈负向关系.应当明确的是，Hou等[3]的理论模型表明，长期市场过度反应与R2的负向关系是由投资情绪和R2的估计方式所暗示的，只要在长期里存在市场过度反应，那么一定会有过度反应导致R2降低*在附录1中，本文对Hou等[3]文中模型和主要结论做了简要介绍..或者说R2与中期动量效应和长期反转效应存在负相关关系.

根据明星分析师与R2显著负相关的事实以及Hou等[3]理论模型的结论，如果投资者对明星分析师报告过度解读而产生过度反应时，则明星分析师在降低R2中的作用就不仅仅局限在信息提供方面.如果明星分析师能够影响投资者情绪，并引起投资者过度反应，则明星分析师降低股价同步性的机制为过度反应机制.但是，目前为止，本文并不能确定究竟是明星分析师的信息提供作用还是对投资者情绪的影响作用更能够解释我国股票市场中明星分析师降低股价同步性现象.

本文研究的目的就在于从投资者过度反应的角度研究明星分析师对股价同步性的影响，并对两种解释低股价同步性的机制进行比较.在我国股票市场中，大部分交易由个人投资者完成，而众多研究表明个人投资者更倾向于表现出过度反应等行为偏差*李心丹等 [9]发现投资者确实存在严重的认知偏差；Chen等[10]相对于美国投资者，我国投资者更倾向于过度自信；Ng 等[11]发现在我国股票市场中，纯反转策略能够获取正的超额收益，且均值反转和动量策略能够击败购买持有策略，表明我国存在过度反应..基于这些事实，本文认为在我国股票市场中个人投资者倾向于对明星分析师报告进行过度反应，从而使明星分析师通过引起过度反应降低股价同步性，而非通过信息提供机制.因此，本文的结论将有助于帮助解释我国股价同步性与分析师跟踪的关系.

本文与Hou等[3]存在以下两个方面区别.首先，本文讨论分析师的异质性特征，区分明星和非明星分析师在引起投资者过度反应方面的差异，并从投资者情绪这一角度考察分析师与股价同步性的关系，而不同于Hou 等[3]考察过度反应与股价同步性的关系.其次，本文将样本限定在我国股票市场范围而非全球范围，这样能够很好地控制国家间制度差异等对实证结果造成的影响.此外，本文与Xu等[2]具有联系，但是区别于他们通过明星分析师的信息提供作用解释股价同步性的降低，本文从明星分析师引起投资者过度反应的机制解释股价同步性的降低.

使用我国A股市场所有股票2003年6月到2013年12月的数据，本文发现：首先，对于全样本，明星分析师对股价同步性具有负向影响.其次，即使明星、非明星分析师具有相似的预测准确度，明星分析师跟踪人数仍然对股价同步性具有负向影响，而非明星分析师对股价同步性的影响不显著，这表明明星分析师的信息提供作用对我国的低股价同步性的解释力有限.第三，预测准确度最高组和最低组明星分析师跟踪股票的平均股价同步性没有显著的差异，意味着明星分析师个人能力并非是降低股价同步性的主要因素.最后，明星分析师跟踪人数以及正向的股价评级调整均能够引起更强的短期动量效应、长期反转效应和异常成交额，这支持了明星分析师引起更大程度市场过度反应论点.上述研究结果都表明，明星分析师主要通过引起市场过度反应降低股价同步性.

基于上述发现，本文的贡献主要体现在以下三点：首先，本文针对我国新兴市场特点，对明星分析师降低R2的机制提供了一种新的基于行为金融学的解释，即明星分析师降低R2的机制与市场过度反应有关，这一发现对于R2的形成机理提供了一个新的视角.其次，本文对信息提供机制和过度反应机制的比较结果进一步表明在我国股票市场中，过度反应机制比信息提供机制具有更强的解释力，对Xu等[2]等文献提供了有力的补充.最后，本文找到了引起市场过度反应的一个来源，并通过一系列实证证据支持了明星分析师的报告会引起市场过度反应.包括Hou 等[3]等在内的已有文献并没有对引起市场过度反应的因素进行界定与分析，本文的证据为Hou等[3]提供了一定的支持，并从来源上对市场过度反应降低R2的机制进行了分析与解释.

1　文献综述与研究假设

与本文相关的第一类文献是关于R2的.传统文献认为R2与信息效率具有负向关系，它首先被Roll[12]用来衡量公司层面信息的含量.Morck等[13]认为，相对于新兴市场国家，发达国家对投资者和产权进行的更好的保护激励了市场基于公司层面信息的交易行为，因此发达国家股票市场具有更低的R2.Durnev等[14]、Jin 等[15]也都证实了R2与市场有效性的负向关系.王亚平等[16]基于我国股市数据的实证发现，机构投资者持股比例的上升会削弱R2与信息透明程度之间的联系，因此，他们认为机构投资者能够提供更多公司层面信息、提高定价效率.潘宁宁等[17]也发现机构投资者通过交易增加了公司层面信息，孔东明等[18]则发现机构投资者的信息提供作用与流动性有关，这些文献也同样认为R2与信息效率存在负相关.

然而，R2与市场效率之间的负向关系也越来越受到质疑.Ashbaugh-Skaife等[6]对多国市场的检验结果表明，R2并不能很好地衡量公司层面信息.Hou等[3]提供了更强的理论分析结果，如果投资者对公司层面信息的反应是无偏的，则当期的R2会下降，整个期间的R2不受影响；但投资者对公司层面信息的认知偏差则会导致R2与市场低效率呈负向关系；同样基于多国市场的实证结果也证实R2是与短期动量效应和长期反转效应具有正向关系.相似的结论还可见于Teoh等[7]、Chang等[8].

与本文相关的第二类文献是关于研究分析师与R2的关系以及明星分析师异质性的.Chan 等[1]认为，由于没有促进公司层面信息的传递，包含中国在内的新兴市场国家的分析师没能降低R2.朱红军等[19]对中国分析师的研究得出了相反的结论，他们认为，即使在排除噪声等因素的影响后，分析师也能通过揭示更多公司层面的信息、提高市场有效性来降低R2.也有研究从其他角度(例如，审计费用[20])考察得出结论认为分析师具有信息提供作用.以上研究并未考虑分析师的异质性，但事实上，由于明星分析师在过去的研究中抵制了利益冲突[21]*关于分析师丑闻的报告屡见不鲜，例如，2011年，“国泰君安自夸自卖长城汽车”；2012年，东方证券分析师对东阿阿胶研报严重失实；上述资料来源于《理财周报》，2012年5月28日.，且具有丰富的一般经验和公司相关的特定研究经验[2]，而提供了更准确的盈余预测和更有价值的荐股报告[4，22，5].基于Chan 等[1]并对分析师的异质性加以考虑后，Xu 等[2]认为，我国的明星分析师因促进公司层面信息的传递而显著地降低了R2.

根据上述两类已有文献，特别是影响股价同步性的机制，明星分析师主要通过两种机制来降低股价同步性.一方面，如果明星分析师提供了更多公司层面信息，且投资者对分析师提供的信息理性地反应，则明星分析师能够降低股价同步性.本文称明星分析师通过提供更多公司层面信息而降低股价同步性的机制为信息机制.另一方面，如果明星分析师直接或间接导致市场存在长期过度反应，而根据Hou 等[3]，过度反应与股价同步性负相关，则明星分析师也能够降低股价同步性.本文称此为过度反应机制.根据两种机制的作用，本文首先提出假设1来检验明星分析师和股价同步性是否存在显著的负相关关系：

假设1相对于非明星分析师，明星分析师与股价同步性显著负相关.

即使确定了明星分析师和股价同步性之间的负向关系，也很难发现明星分析师在降低股价同步性中起到的究竟是哪类作用.如果R2与公司层面信息相联系；且如Xu 等[2]所发现，明星分析师代表盈余预测能力更准确的一类分析师，能够提供更多公司层面信息.那么，根据Hou 等[3]的模型，如果投资者能对明星、非明星分析师以及不同类型的明星分析师所提供的公司层面信息进行理性反应，那么明星分析师则是通过信息机制来降低当期R2的.根据信息机制，本文得到两个推论：1)如果明星、非明星分析师都提供同样准确程度的预测时，投资者应该对两类分析师做出相似的反应，此时两类分析师对R2的影响应该相似；2)即使都是明星分析师，如果存在预测准确度方面的差异，投资者也能准确的识别这种差异，而使用更加准确的明星分析师报告，此时不同准确度的明星分析师对R2的影响具有显著差异，或不同准确度的明星分析师所跟踪股票的R2具有显著差异.如果上述两个推论被证实，那么明星分析师可能是通过提供了更多公司层面信息而降低了R2；反之，如果被证伪，则明星分析师存在降低R2的其他机制.

为了通过检验上述两个推论来检验信息机制在降低R2方面的解释力，提出如下假设2：

假设2a如果明星分析师通过信息机制降低股价同步性，当两类分析师具有相似预测准确度时，明星、非明星分析师对股价同步性的影响无差异；对于明星分析师跟踪的股票，预测准确度最高组和最低组的股价同步性具有显著的差异.

假设2b如果明星分析师通过信息机制以外机制降低股价同步性，当两类分析师具有相似预测准确度时，明星分析师相对于非明星分析师能够显著降低股价同步性；对于明星分析师跟踪的股票，预测准确度最高组和最低组的股价同步性不具有显著的差异.

如果假设2b被证实，那么明星分析师降低股价同步性的机制是什么呢？Hou 等[3]的理论分析已经明确的指出，当投资者对公司层面信息的反应不理性时，特别是当投资者对公司层面信息的反应在长期里都是过度反应时，那么R2一定与动量和反转效应呈反比.也就是说，当投资者对信息的反应不理性时，股价中存在的过度反应是R2降低的主要原因.

在研究明星分析师通过引起市场过度反应而降低股价同步性前，本文首先需要考察在中国股票市场中，是否同样存在市场过度反应与股价同步性之间的负向关系.因此，根据Hou等[3]，提出如下假设3：

假设3a股价同步性越低的股票在短期里具有更强的动量效应；

假设3b股价同步性越高的股票在中长期里具有更强的反转效应；

那么，如果明星分析师能够引起市场过度反应，则明星分析师降低R2的事实则主要是由引起市场过度反应所解释.

明星分析师之所以能够引起市场过度反应，主要原因是明星分析师相比较于非明星分析师更能引起投资者注意，当投资者根据明星分析师报告进入市场交易时，他们对股票的估值产生偏差，而投资者通常表现出的羊群效应进一步放大了估值偏差，导致市场过度反应的产生.

综上，根据本文关于过度反应的论据，明星分析师能够引起投资者过度反应.如果这一论据合理，则本文将发现明星分析师跟踪人数与投资者过度反应之间存在正相关关系.由于过度反应无法直接被度量，因此，根据Jegadeesh等[23]、Jegadeesh等[24]、Hou等[3]和许年行等[25]，将上述假设重新表述为：

假设4a明星分析师跟踪人数越高的股票在短期里具有更强的动量效应；

假设4b明星分析师跟踪人数越高的股票在中长期里具有更强的反转效应；

假设4c明星分析师做出评级调整的股票具有更高的异常成交额.

为了使上述逻辑关系及本文假设与现有文献之间的关系更加清晰，绘制如下关系图：

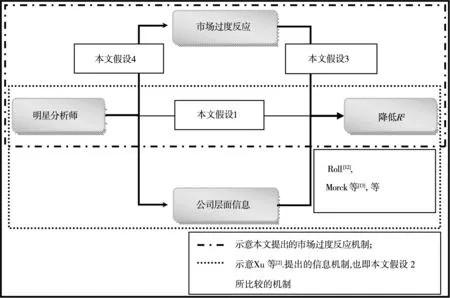
图1　明星分析师降低股价同步性的两种机制对比以及本文假设关系

2　数据样本与变量设定

2.1样本选择与数据来源

本文以沪深两市上市的所有A股股票为样本，时间范围从2003年6月至2013年12月，并对样本按如下标准进行筛选：1)剔除金融类公司；2)受到特别处理，即股票代码中包含ST、*ST以及PT的股票被剔除；3)必须在实证分析前一年发行上市，剔除年交易日少于180天的股票[26]，以避免微观结构因素对实证结果产生严重的影响；4)剔除数据缺失的样本.经过以上筛选，本文最终得到7 119个公司——年度样本.样本内股票的交易数据和财务报表来自于国泰安数据库(CSMAR).

分析师盈余预测数据也来自于CSMAR.如果分析师在当年对同一上市公司发布多份预测报告，本文仅保留最后一次报告.稳健性检验使用了分析师的荐股报告，这些报告同样来自于CSMAR.荐股评级被标准化为5级，从1至5分别代表“买入”、“增持”、“中性”、“减持”及“卖出”，因此，评级越高，分析师对该股的看法越悲观.在2004年至2013年内，本文共得到针对上述样本公司发布的45 039份荐股报告，其中2 444份评级高于或等于3.此外，在区分明星、非明星分析师时，本文使用了《新财富》最佳分析师排名，上榜分析师名单及评选时间从《新财富》网站刊登的历届“最佳分析师”获奖名单中整理得到.

2.2变量设定

2.2.1股价同步性(R2)

借鉴Gul 等[27]、Hou 等[3]以及Xu 等[2]，本文使用周收益率数据对下述模型进行回归以得到R2，记为Rsq，即

ri,w=αi,w+βi,wrm,w+γi,wrind,w+εi,w

(1)

其中ri,w为股票i在第w周的收益率，rm, w为第w周A股市场收益率，rind, w为第w周股票i所在行业的总市值加权平均收益率，对于股票i，在计算其行业收益率时，其自身收益率被排除在外；在计算其市场收益率时，其所在行业收益率被排除在外，以避免估计结果受其自身影响，即避免模型(1)的估计结果受多重共线性的影响.Rsq则为模型(1)估计结果的可决系数.根据Hou 等[3]，本文使用全样本期间数据来估计模型(1)*仅使用一年样本无法考察投资者的过度反应行为.当本文使用约3年(180周)数据时，得到的实证结果相似..

由于Rsq被限定在0和1的闭区间内*在模型(1)的所有回归结果中，没有Rsq小于0的情况出现.，根据Morck等[13]，本文在实证中使用Rsq的对数变换形式，即

LnRsq,i=ln[Rsq,i/(1-Rsq,i)]

(2)

其中LnRsq,i为第i只股票股价同步性的衡量指标.LnRsq,i越高，股价波动更多地被市场波动所解释.

2.2.2分析师跟踪人数

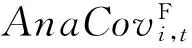
2.2.3异常成交额

市场对分析师的报告反应过度的表现之一为股票具有异常的成交额.因此，为了衡量市场是否对分析师的报告过度反应，根据Jegadeesh等[24]的方法，本文使用报告发布后一定时期的平均成交额对发布前后时期平均成交额的比率来衡量报告所引起的异常成交额.记分析师在第t期前对公司i发布的预测报告引起的该公司股票在第t期中的异常成交额为AVoli,t，则

(3)

其中Volume为股票的月成交额，M为所估计的总月数.

2.2.4预测偏差

分析师对市盈率(EPS)预测值与真实值的偏离程度度量了分析师盈余预测的准确度.根据Hong等[28]和Xu等[2]的方法，本文使用相对预测偏差，即EPS预测值和真实值之差的绝对值对股价的比值来衡量预测的偏离程度.记分析师j对公司i第y年盈余的预测偏差为FEj,i,y，则

(4)

其中F_EPSj,i,y为分析师j对公司i第y年EPS的预测值，EPSi,y为公司i第y年EPS的真实值，Pricei,y为公司i第y年的年终收盘价.

2.2.5控制变量

本文在文中控制如下两组变量：一是影响R2的变量.根据Piotroski等[29]，Chan等[1]，Gul等[27]，以及Xu等[2]等研究，本文设定如下变量来控制其它因素对R2的影响：1)股权集中度，记为Top1，为上年末公司第一大股东持股比例；2)机构持股比例，记为InsHold，为上年末机构投资者持股占总股数的比例；3)国有股比例，记为GovHold，为上年末国有股占公司总股数的比例；4)换手率，记为Turnover，为股票当年成交额除以当年末的总市值；5)公司规模，记为LnSize，为公司在上年末总市值的自然对数；6)公司市值对账面价值比，记为MB，为公司上年末的总市值除以净资产总额；7)行业内公司数量，记为IndNum，为公司所属行业内上年末的上市公司数量；8)行业规模，记为LnIndSize，为公司所属行业上年末总市值的自然对数形式.

二是影响股票收益率的变量.根据Jegadeesh[30]，Hou等[3]，以及鲁臻等[31]的研究结果，本文包含以下变量来控制其它因素对股票收益率的影响：1)公司规模，记为LnSize，为公司上年末总市值的自然对数；2)账面价值对市值的比率，记为LnBM，为公司上年末净资产账面价值对总市值比率的自然对数；3)上期收益率，记为Ret(-1:-1)*鲁臻等[31]的研究发现，在中国股票市场上存在短期的反转效应；同时，Jegadeesh [30]也认为存在一个月的短期反转效应.因此，为了控制短期反转效应，本文也同Hou 等[3]一样引入该控制变量..

3　实证分析

3.1描述性统计

表1给出了所有变量的描述性统计结果，平均来看，每家公司每年的分析师跟踪人数为10.83，其中2.041为明星分析师；盈余预测偏差为0.021 0；第一大股东持股为38.2%，国有持股为13.5%，机构持股为21.1%.

表1　所有变量描述性统计

表2给出了按明星分析师跟踪人数分组和评级调整分组的描述性统计结果.首先，本文按照如下步骤对股票按明星分析师跟踪人数分组考察主要变量的均值特征：1)对2004年6月到2013年12月中的各月，计算股票在前2月到前12月的明星分析师跟踪人数(StarF)；2)每月按明星分析师跟踪人数将股票分为3个组合，第1个组中股票的明星分析师跟踪人数为0，第2个组中股票的明星分析师跟踪人数低于非0跟踪人数序列的75%分位数，第3个组合包含剩余的股票*本文选用75%分位数作为分组标准，而非通行的50%分位数，这是由明星分析师跟踪人数的特征所决定的.描述性统计结果表明，明星分析师跟踪人数的50%分位数为1，75%分位数为3.若采用50%分位数来区分高明星分析师跟踪人数和低明星分析师跟踪人数，则高明星分析师跟踪人数组的跟踪人数大于1，相对于2.04的平均水平，高明星分析师跟踪人数组的跟踪人数并非高.而本文假设明星分析师跟踪人数越高，则市场过度反应越强，50%的划分方法难以对本文的假设进行验证.因此，本文选取75%分位数作为分组标准，该标准也即大于平均值水平的标准.；3)计算各组合内StarF、Rsq、月收益率(Ret)、月度Turnover、LnSize、MB、InsHold以及GovHold的横截面算术平均值；4)计算上述结果在时间序列上的平均值，得到按明星分析师跟踪人数排序的变量特征.该结果列在表2的Panel A中.从中可知，对于第2、3组，平均明星分析师跟踪人数为2.19和6.93，对应的R2分别为0.46和0.43，明星分析师跟踪人数和R2之间表现出负相关关系.对于第1、3组，平均明星分析师跟踪人数为0和6.93，R2分别为0.48和0.43.

按明星、非明星分析师类别分组和评级调整分组的描述性统计结果分别列在表2的Panel B和Panel C中.从Panel B中可知，平均来看，明星、非明星分析师所跟踪股票的R2分别为0.43和0.44，而明星分析师比非明星分析师在调整评级时更悲观，平均调整分别为-0.011和-0.006.平均收益率分别是1.24%和0.53%.从Panel C中可知，正向评级调整报告中的15%由明星分析师发布，对应股票的R2为0.45.评级未调整报告中的23%由明星分析师发布，对应股票的R2同样为0.45.上述结果表明，尽管明星分析师对股票做出正向评级调整的可能性较低，但是其调整股票的收益率比非明星分析师调整股票的收益率更高，与投资者过度反应的假设相一致.

表2分组描述性统计

Table 2 Summary statistics by groups

Panel A： 按明星分析师跟踪人数分组

StarFgroupStarFRsqRet(%)TurnoverLnSizeMBInsHoldGovHoldN100.481.803.8827.663.020.180.15251822.190.461.603.1722.603.290.220.13366336.930.432.102.2623.763.390.270.12938

Panel B： 按明星、非明星分析师分组

StarFgroupRsqRevisionStdRecRet(%)TurnoverLnSizeMBInsHoldGovHoldNNstar0.44-0.0061.770.522.8823.363.580.250.1535120Star0.43-0.0111.701.242.6423.543.670.260.149919

Panel C： 按评级调整分组

RevisionStarRsqStdRecRet(%)TurnoverLnSizeMBInsHoldGovHoldN<00.150.451.372.542.9423.323.720.240.162729=00.230.451.730.832.7923.433.620.260.1539866

在表3中，本文给出了所有变量相关系数的Pearson检验结果.从中可知，明星分析师跟踪人数与R2、盈余预测偏差与R2、以及股价与R2之间均呈现出显著的负相关关系.

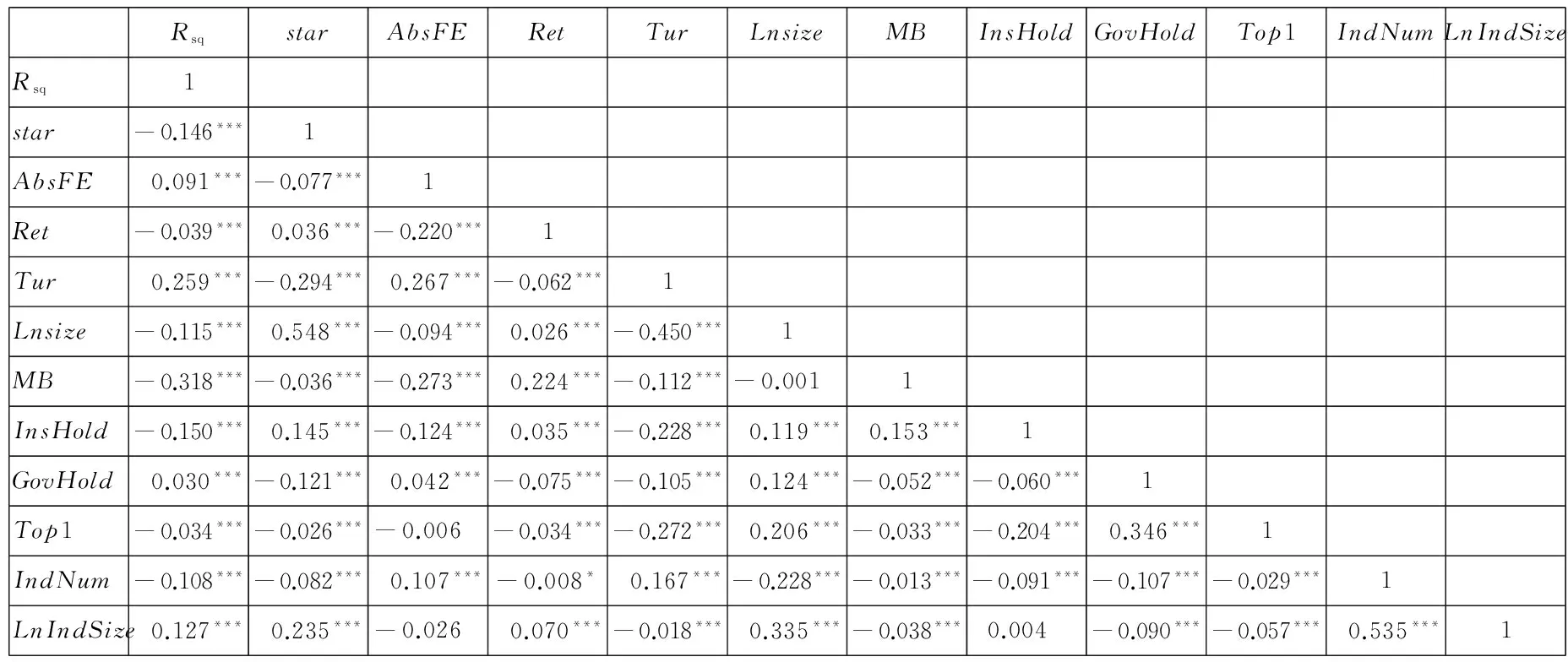
表3　相关系数的Pearson检验

3.2明星分析师与R2

与Xu等[2]相似，本文首先考察明星、非明星分析师跟踪人数对股价同步性的影响，即对下列模型(5)进行LSDV估计：

ρtYeary+δiIndustryi+εi,y

(5)

其中Ana为分别取明星分析师跟踪人数(StarF)或非明星分析师跟踪人数(NonStarF)；Control为包含上文设定的对R2具有影响的控制变量.Year和Industry分别表示年份和行业虚拟变量，用以控制时间和行业效应.根据Petersen[32]，本文对LSDV估计系数的标准误差采用基于年度和行业两个维度的Cluster修正.估计结果列在表4中.

从表4的Panel A中可知，不控制非明星分析师的影响时，明星分析师对股价同步性具有负向影响，且在1%水平下显著.而当不控制明星分析师的影响时，非明星分析师对股价同步性的影响也为负，但是不具有统计意义上的显著性.同时考虑两类分析师的影响时，结果与上述相似.因而，上述结果证实了本文的假设1.

表4给出的结果与Xu等[2]的结果略有差异，他们发现非明星分析师对股价同步性具有显著的正向影响.本文关于非明星分析师的估计结果虽然为负，但是无论从经济意义还是统计意义来看，其对股价同步性的负向影响没有明星分析师的影响显著.因此，该结果不妨碍本文对“明星分析师更能引起市场过度反应，从而导致股价同步性更低”这一假说进行验证.

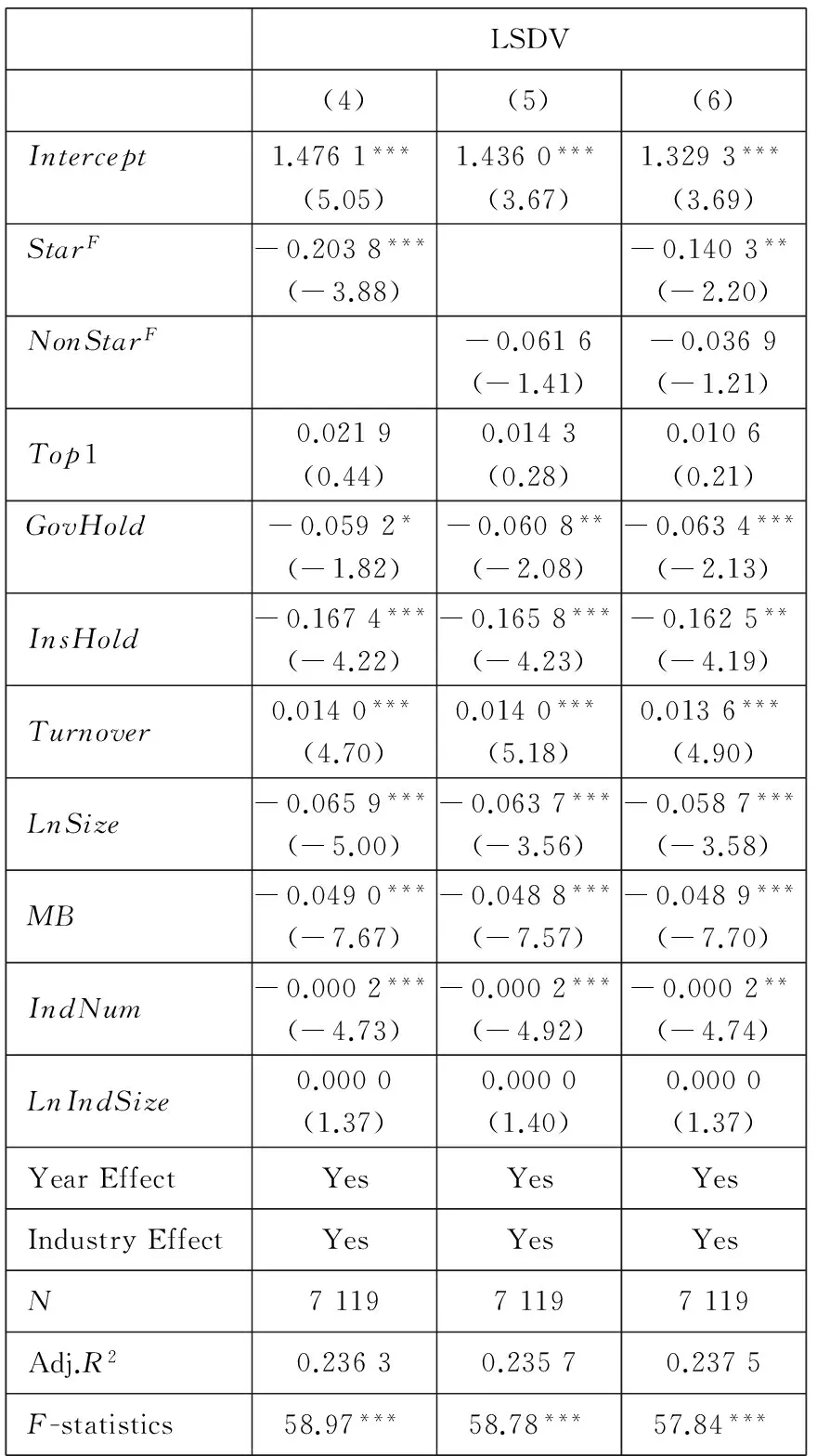
表4　分析师跟踪人数与股价同步性，全样本LSDV估计结果

其中，估计系数的标准差经过行业和年份两个维度上的Cluster修正.

上述模型(5)估计结果可能受到严重的内生性问题的影响，即某种公司特征或市场特征与股价同步性相联系，而这种未知的因素又是明星分析师选择跟踪股票的影响因素；或者明星分析师更偏向于选择股价同步性更低的股票进行跟踪.那么，上述结果就并非表明明星分析师能够显著降低股价同步性.为了减轻内生性问题的影响，本文使用2SLS估计模型(5).根据Yu[33]和Xu 等[2]，2SLS所用的工具变量为预期分析师跟踪人数和波动率.

预期分析师跟踪人数的计算公式为

(6)

其中expAna为预期分析师跟踪人数，分别为明星分析师跟踪人数(expStarF)或非明星分析师跟踪人数(expNonStarF).brokersize是对公司i跟踪的分析师所在券商k在y年中雇佣的所有分析师人数.当证券公司增加(或减少)其规模时，更多(或更少)的分析师被雇佣，跟踪人数也随之增加(或者减少).由此，证券公司规模与跟踪人数密切联系.更重要的是，证券公司规模的调整不随某一个上市公司特征所影响.因此，预期分析师跟踪人数是较好的工具变量.

波动率是股票在t年中周收益率的标准差.

当然，首先，分析师所在券商规模变化时，某一公司或某一行业的分析师跟踪人数并不一定受到影响，除非券商同比例减少跟踪各行业的分析师人数.其次，波动率增大时，市场也并不一定对分析师的需求增大，除非分析师在资本市场中提供更多且准确的信息.因此，上述两个工具变量的有效性有待检验，为此，本文将在给出2SLS回归后同时汇报Godfrey检验结果.

2SLS的具体估计方法是：

1)在第一步中做如下模型的估计

Anai,y=α0+θ1expAnai,y+θ2Volatilityi,y+

δiIndustryi+εi,y

(7)

2)在第二步中，利用模型(7)得到Ana的估计值，然后将估计值带入模型(5)进行回归.同样，估计系数的标准误差采用行业和年份两个维度的Cluster修正.2SLS的估计结果列在表5中.Godfrey检验结果显示，本文选取的两个工具变量均为强工具变量(分别对明星和非明星分析师跟踪人数回归时，对两类分析师的Godfrey检验的R2分别为0.201和0.400；同时对两类分析师回归时，Godfrey检验的R2分别为0.334和0.199).

表5的结果显示，2SLS第二阶段的估计结果同表4中的结果相似，非明星分析师对股价同步性的影响为负，但是不显著；明星分析师对股价同步性的影响仍然显著为负.同样，无论从经济意义还是统计意义上来看，非明星分析师的影响都不及明星分析师的影响显著.

3.3明星分析师盈余预测准确度与R2

根据如下步骤对假设2第一部分进行检验：

1)选取同时包含明星、非明星分析师跟踪的股票，计算两类分析师盈余预测偏差均值，然后根据预测偏差的差异程度将所有股票分为5个Diff组，第1组的两类分析师具有相似的预测准确度(或偏差)，第5组的两类分析师在预测准确度上存在最大差异.

2)使用每组样本在公司层面对模型(5)做LSDV回归.结果列在表6的Panel A中.

为了减轻内生性问题带来的估计偏差问题，本文同样使用3.2节中的2SLS法分组估计明星、非明星分析师对股价同步性影响的差异.第一阶段分组对模型(7)回归得到分析师的估计值，第二阶段里利用估计值做模型(5)的估计.第二阶段的估计结果列在表6的Panel B中.

在检验假设2第二部分时采用如下步骤：

1)剔除无明星分析师跟踪的公司，并计算明星分析师对每家公司盈余预测偏差的均值；然后，根据FE的5个等分位数将所有公司分为5个FE组，第1组的预测偏差最小，第5组的预测偏差最大.

2)从2004年6月到2013年12月，对各FE组计算各年R2的均值、T检验的P值以及Wilcox检验的P值，并给出FE1组和FE5组R2比较的T检验的P值和Wilcox检验的P值.估计结果列在表6的Panel C中.

表5　分析师跟踪人数与股价同步性，全样本2SLS估计结果

从表6的Panel A中可知，对于预测偏差最相似的第1组，同时考察两类分析师时，明星分析师跟踪人数仍然在10%水平下显著降低股价同步性，而非明星分析师的影响虽然为负，但不显著，t值仅有-1.02.在第3、5组，明星分析师的影响依然显著为负，而非明星分析师的影响不显著.在第2、4组，两类分析师对股价同步性的影响都变得不显著.

表6中Panel A的实证设计能够区分明星分析师究竟是否起到信息提供作用.如果信息提供作用是最主要的作用，当两类分析师具有相似的信息提供能力，即具有相似的预测偏差时，他们对股价同步性的影响也应该相似.但是上述实证结果却与之相反，即明星分析师相对于非明星分析师具有更高的信息提供能力无法解释表6中Panel A的结果.而该结果却恰恰能够证明明星分析师通过其他机制降低了R2.

表6中Panel B给出的2SLS估计结果表明，修正了内生性问题后，即使明星、非明星分析师提供相似程度的信息，两类分析师对股价同步性的影响也具有显著差异，明星分析师依然显著降低R2，而非明星分析师则没有.

表6中Panel C的结果显示，虽然FE1组的R2比FE5组小，分别为0.438 2和0.441 1，但这一差异并无统计上的显著性.该结果表明，相对于能力较差的明星分析师，能力更强的明星分析师没有显著的降低股价同步性，这一结果同样无法用明星分析师的信息提供作用来解释.因此，综上来看，明星分析师降低股价同步性的主要原因并非是因为他们提供了更多的公司层面信息.而应由其他机制所解释.

资本市场中意见分歧的存在意味着信息不对称，投资者意见分歧会导致股票收益率在年报公告日做出负向调整[34]，IPO询价意见分歧则导致IPO定价过高及未来股价的大幅度下跌[35].分析师意见分歧大同样意味着股票存在较高程度的信息不对称，并且反应市场对股价存在乐观情绪及未来股价的下跌[36].综上，分析师意见分歧越大，股票的估值结果可能存在越大的偏差，市场过度反应可能越大.表6的结果表明，即使明星分析师提高预测准确性，也难以降低(非)明星分析师存在较大意见分歧，即存在较高程度市场过度反应的股票之股价同步性.因此，明星分析师降低股价同步性的渠道主要是通过引起市场过度反应，而非提供更多信息.

表6预测准确度与股价同步性

Table 6 Forecast accuracy and price synchronicity

Panel A： 不同预测准确度下的股价同步性回归结果

Panel A: Regression results for price synchronicity under different forecast accuracy

Forecastaccuracy(FE)1(leastdifference)2345(largestdifference)StarF-0.2464*(-1.90)-0.0907(-0.83)-0.1376*(-1.75)-0.1692(-1.32)-0.1180*(-1.75)NonStarF-0.0323(-1.02)0.0024(0.06)-0.0295(-0.85)-0.0154(-0.29)-0.0550(-1.09)Top10.0232(0.16)0.1228(1.08)0.0286(0.27)0.0031(0.02)0.1253(1.32)GovHold0.1356(0.98)-0.0099(-0.20)-0.1060(-1.54)0.0185(0.21)-0.2047*(-1.73)InsHold0.0295(0.38)-0.0567(-0.82)-0.1959***(-2.69)-0.1400**(-2.15)-0.2166***(-3.15)Turnover0.0221(1.38)0.0218***(2.80)0.0157**(2.13)0.0113*(1.77)0.0131***(3.81)LnSize-0.0663**(-2.35)-0.1307***(-4.75)-0.0531*(-1.68)-0.0993**(-2.50)-0.0435**(-2.32)MB-0.0576***(-4.62)-0.0358***(-8.92)-0.0493***(-6.38)-0.0465***(-4.30)-0.0564***(-7.47)IndNum-0.0007***(-2.68)-0.0001(-1.24)-0.0001(-0.71)0.0002(0.90)0.0000(0.28)LnIndSize0.0000(0.81)0.0000*(1.93)-0.0000(-0.04)0.0000(0.13)0.0000(0.69)YeareffectYesYesYesYesYesIndustryeffectYesYesYesYesYesN929921920910921Adj.R0.26080.28810.24960.24910.2496F9.40***10.80***8.84***8.94***9.05***

其中，估计系数的标准差经过行业和年份两个维度上的Cluster修正.

Panel B：不同预测准确度下的股价同步性回归结果(2SLS第二阶段回归结果)

Panel B: 2SLS regression results for price synchronicity under different forecast accuracy

Forecastaccuracy(FE)1(leastdifference)2345(largestdifference)StarF-0.2452**(-2.49)-0.2706*(-1.72)-0.0528(-0.17)-0.0426(-0.16)-0.1196(-0.27)NonStarF-0.0084(-0.08)0.0333(0.51)-0.0740(-1.04)-0.1135(-1.05)-0.0669(-0.48)Top10.0725(0.48)0.0746(0.77)0.1402*(1.69)-0.1784(-1.06)0.0531(0.58)GovHold0.0655(0.40)0.0435(0.47)-0.1318*(-1.83)0.0216(0.24)-0.1878*(-1.69)InsHold-0.0327(-0.25)-0.0375(-0.75)-0.1217*(-1.81)-0.1938***(-2.94)-0.2263***(-3.76)Turnover0.0214(1.26)0.0110*(1.87)0.0174***(2.59)0.0138*(1.88)0.0142***(3.20)LnSize-0.0831**(-2.41)-0.1336***(-3.38)-0.0365(-1.28)-0.0787(-1.58)-0.0402(-1.32)MB-0.0590***(-4.57)-0.0364***(-9.84)-0.0571***(-5.33)-0.0490***(-3.85)-0.0475***(-4.11)IndNum-0.0008**(-2.27)-0.0002*(-1.89)0.0000(0.08)0.0000(0.03)0.0001(1.12)LnIndSize0.0000(1.43)0.0000***(2.66)-0.0000(-1.16)0.0000(0.20)0.0000(0.38)YeareffectYesYesYesYesYesIndustryeffectYesYesYesYesYesN944938928914930Adj.R0.25510.28730.26210.24170.2352F9.50***11.21***9.66***9.09***8.93***

其中，估计系数的标准差经过行业和年份两个维度上的Cluster修正.

Panel C： 明星分析师预测准确度

Panel C: Star analysts’ forecast accuracy

Forecastaccuracy(FE)123451-5AverageR20.4382***0.4387***0.4387***0.4384***0.4411***-0.0029t-test(p-value)0.00000.00000.00000.00000.00000.4379Wilcoxtest(p-value)0.00000.00000.00000.00000.00000.4103

3.4股价同步性与市场过度反应

3.4.1股价同步性与动量效应

借鉴Hou等[3]，本文使用“双排序分组方法”来考察股价同步性与动量效应之间的关系，具体方法如下：

(1)对于第t月的所有样本股票，计算t-12月到t-2月持有期收益率，并根据分位数将股票分为5个Mom组，Mom1组股票在过去的收益率表现最差，Mom5组在过去的表现最好.

(2)对每个Mom组的股票，按R2分为3组，其中第1个R2组中股价同步性最低，第3组股价同步性最高.

(3)计算每个R2-Mom组合中股票当月收益率的横截面算术平均值*为了提高每个R2-Mom组中股票收益率相关计算的准确性，本文在实证中要求每个Star组的股票数不低于25只.,Mom5组股票收益率均值减Mom1组收益率均值便是该组的明星分析师所引起的动量效应.除了算术平均值，本文还给出Mom5组与Mom1组收益率之差的总市值加权平均值.

(4)将2004年6月到2013年12月各月的结果做时间序列上的平均，并计算相应的t统计量，实证结果列在表7中.

Ball等[37]认为风险特征的时变性会影响对于动量效应的实证分析，因此，本文使用CAPM模型中的市场风险因子对上述原始收益率进行调整.此外，Zarowin[38]认为规模效应会影响动量效应的实证检验，因此，本文进一步使用Fama-French[39]三因子模型中的市场风险因子、公司规模因子以及成长性因子对上述的结果进行调整.

表7的结果显示，R2最低组，股价同步性最低，动量效应是3个R2组中最高的，且在5%水平下显著.R2最高组，股价同步性最高，动量效应小于第1个R2组，且不显著.即股价同步性与股价动力效应正相关，这一结果证实了本文提出的假设3a.

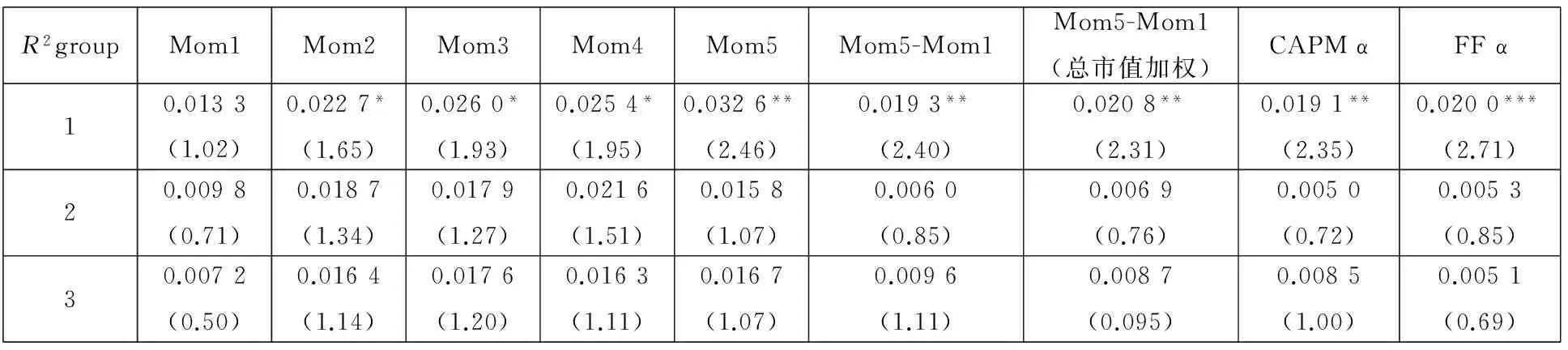
表7　股价同步性与股价的动量效应

3.4.2股价同步性与反转效应

本文计算每个R2-Mom组中所有股票在t～t+5、t～t+11、t+12～t+35持有期收益率的算术平均值、总市值加权平均值和经风险因子调整的异常收益率，从而考察股票的反转效应.该结果列在表8中.

以Panel C的原始收益率为例，股价同步性最低的第1个R2组，反转效应在1%水平下显著为-7.77%；而股价同步性最高的第3个R2组，反转效应仅在10%水平下显著为-4.53%，收益率高于第1个R2组.即股价同步性也与未来反转效应正相关，这一结论同样证实了本文提出的假设3b.

表8股价同步性与股价的反转效应

Table 8 Price synchronicity and reversal effect

Panel A:t～t+5月

Panel A:t～t+5 month

R2groupMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(总市值加权)CAPMαFFα10.0650*(1.87)0.0804**(2.22)0.0888**(2.42)0.0738**(2.01)0.0732*(1.80)0.0082(0.59)0.0079(044)0.0066(0.47)-0.0034(-0.25)20.0677**(1.99)0.0809**(2.38)0.0910***(2.62)0.0846**(2.36)0.0804**(2.19)0.0127(1.04)0.1103(0.82)0.0115(0.94)0.0079(0.64)30.0793**(2.39)0.1032***(3.12)0.1148***(3.34)0.1061***(3.34)0.1335***(4.10)0.0542***(3.92)0.0509***(3.28)0.0542***(3.88)0.0504***(3.67)

Panel B:t～t+11月

Panel B:t～t+11 month

R2groupMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(总市值加权)CAPMαFFα10.1198**(2.48)0.1376***(2.74)0.1415***(2.81)0.1277**(2.46)0.1172**(2.07)-0.0026(-0.15)-0.0039(-0.82)-0.0056(-0.33)-0.0183(-1.09)20.1243***(2.66)0.1342***(2.90)0.1443***(3.06)0.1425***(2.88)0.1243**(2.50)-0.0001(-0.01)-0.0017(-0.24)-0.0021(-0.14)-0.0081(-0.54)30.1415***(3.13)0.1656***(3.74)0.1830***(3.88)0.1674***(3.83)0.2024***(4.65)0.0609***(3.47)0.0631***(3.05)0.0601***(3.39)0.0552***(3.03)

Panel C:t+12～t+35月

Panel C:t+12～t+35 month

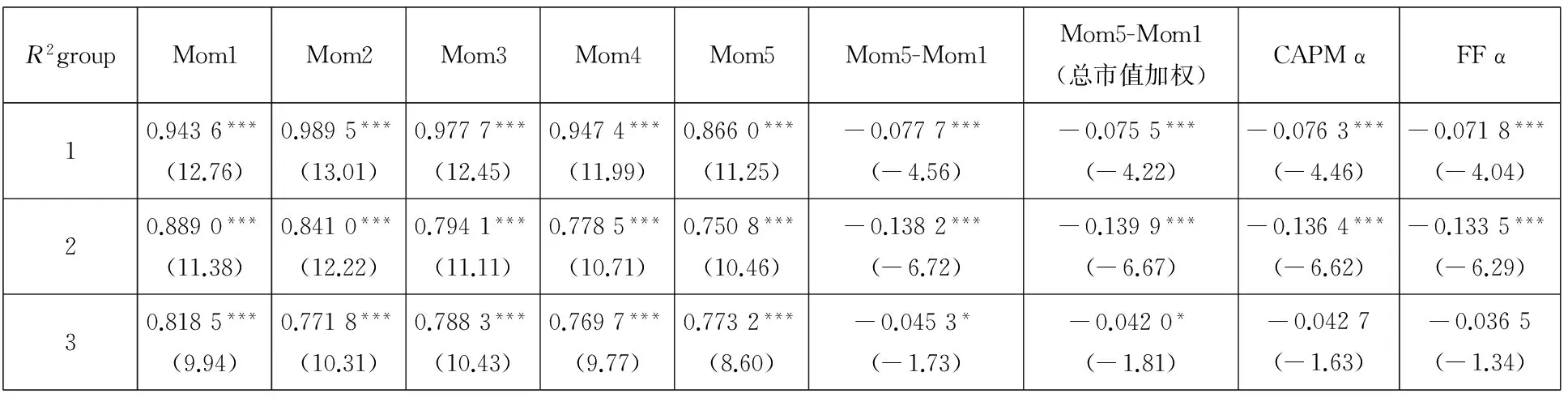
R2groupMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(总市值加权)CAPMαFFα10.9436***(12.76)0.9895***(13.01)0.9777***(12.45)0.9474***(11.99)0.8660***(11.25)-0.0777***(-4.56)-0.0755***(-4.22)-0.0763***(-4.46)-0.0718***(-4.04)20.8890***(11.38)0.8410***(12.22)0.7941***(11.11)0.7785***(10.71)0.7508***(10.46)-0.1382***(-6.72)-0.1399***(-6.67)-0.1364***(-6.62)-0.1335***(-6.29)30.8185***(9.94)0.7718***(10.31)0.7883***(10.43)0.7697***(9.77)0.7732***(8.60)-0.0453*(-1.73)-0.0420*(-1.81)-0.0427(-1.63)-0.0365(-1.34)

综合表7和表8的结果来看，在我国股票市场中同样存在支持Hou等[3]的证据，即影响股价同步性的机制主要是市场过度反应.当市场存在更大程度的过度反应，股价同步性也会降低.

3.5明星分析师与市场过度反应

3.5.1明星分析师与动量效应

借鉴Hou等[3]，本文使用“双排序分组方法”来考察明星分析师所引起的动量效应，具体方法如下：

1)对于第t月的所有样本股票，计算t～12月到t～2月持有期收益率，并根据分位数将股票分为5个Mom组，Mom1组股票在过去的收益率表现最差，Mom5组在过去的表现最好.

2)对每个Mom组的股票，按StarF分为3组，其中第1个Star组中股票的明星分析师跟踪人数为0，第2个Star组中股票的明星分析师跟踪人数小于非0明星分析师跟踪人数序列的75%分位数，剩下的股票被分在第3个Star组中.

3)计算每个Star-Mom组合中股票当月收益率的横截面算术平均值*同前一样，本文在实证中要求每个Star组的股票数不低于25只.，Mom5组股票收益率均值减Mom1组收益率均值便是该组的明星分析师所引起的动量效应.除了算术平均值，本文还给出Mom5组与Mom1组收益率之差的总市值加权平均值.

4)将2004年6月到2013年12月各月的结果做时间序列上的平均，并计算相应的t统计量，实证结果列在表9中.

除了原始收益率，同样给出经CAPM模型和Fama-French模型调整收益率的实证结果.

表9的结果显示：在StarF最低组中，动量效应为0.26%，且不显著；而在StarF最高的组中，动量效应在10%水平下显著为0.95%，且第1组和第3组的动量效应存在着显著的差别，F统计量为7.35.使用总市值加权平均、经市场风险因子调整以及经市场风险因子、公司规模因子和成长性因子调整的异常收益率得到的结果也显示明星分析师跟踪人数与动量效应之间仍然存在显著的正相关关系.上述结果支持了本文的假设4a.

表9　明星分析师与股价的动量效应

3.5.2明星分析师与反转效应

该检验方法与3.5.1中方法类似，不同之处在于计算每个Star-Mom组中所有股票在t～t+5、t～t+11、t+12 ～t+35持有期收益率的算术平均值、总市值加权平均值和经风险因子调整的异常收益率.该结果列在表10中.

Panel A的结果显示，在StarF最低的组没有反转效应，Mom5组和Mom1组之差仍然为正；在StarF最高的组中，反转效应在5%水平下显著为-3.98%；同样，F统计量显示明星分析师跟踪人数最高组相对于第1组具有差异显著的反转效应.CAPM和Fama-Fench模型给出的结果相似.Panel B、Panel C给出的第t月到t+11月和第t+12月到第t+35月的结果也与之相似.这些结果均一致表明，明星分析师跟踪人数与反转效应之间存在显著的正相关关系，支持了本文的假设4b.

表10明星分析师与股价的反转效应

Table 10 Star analysts and reversal effect

Panel A:t～t+5月

Panel A:t～t+5 month

StarFgroupMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(总市值加权)CAPMαFFα10.0833***0.1025***0.1075***0.0957***0.0955***0.01220.0120*0.01180.0145(3.30)(3.82)(3.94)(3.50)(3.59)(1.30)(1.69)(1.25)(1.56)20.0472*0.0555*0.04640.04400.0241-0.0231-0.0195**-0.0255*-0.0173(1.72)(1.75)(1.27)(1.26)(0.65)(-1.49)(-2.05)(-1.68)(-1.12)30.0341**0.0241***0.03060.0400**-0.0057**-0.0398**-0.0351**-0.0409**-0.0303*(1.96)(3.76)(0.96)(2.18)(-2.06)(-2.24)(-2.17)(-2.28)(-1.68)

Panel B:t～t+11月

Panel B:t～t+11 month

StarFgroupMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(总市值加权)CAPMαFFα10.1364***0.1616***0.1646***0.1527***0.1437***0.00730.00660.00540.0059(3.96)(4.51)(4.44)(4.02)(3.95)(0.62)(1.05)(0.45)(0.49)20.06740.0752*0.06610.06150.0271-0.0404**-0.0392**-0.0416**-0.0332*(1.32)(1.76)(1.36)(1.31)(0.56)(-2.17)(-2.36)(-2.23)(-1.71)30.0503***0.03150.0313**0.0422-0.0170***-0.0674***-0.0691**-0.0663***-0.0546**(3.03)(0.73)(2.37)(0.94)(-3.17)(-2.78)(-2.18)(-2.72)(-2.16)

Panel C:t+12～t+35月

Panel C:t+12～t+35 month

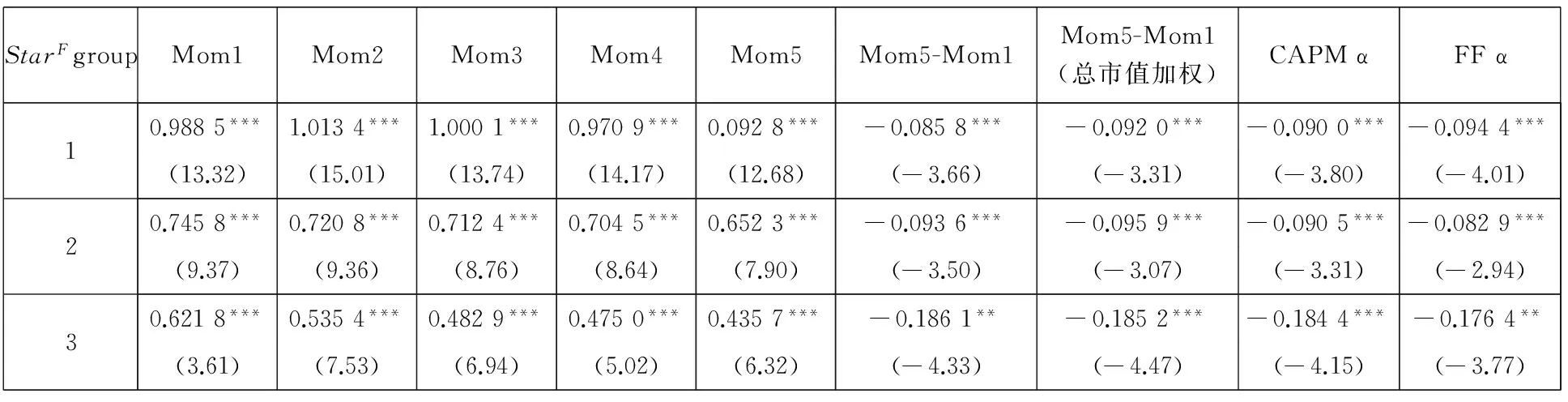
StarFgroupMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(总市值加权)CAPMαFFα10.9885***1.0134***1.0001***0.9709***0.0928***-0.0858***-0.0920***-0.0900***-0.0944***(13.32)(15.01)(13.74)(14.17)(12.68)(-3.66)(-3.31)(-3.80)(-4.01)20.7458***0.7208***0.7124***0.7045***0.6523***-0.0936***-0.0959***-0.0905***-0.0829***(9.37)(9.36)(8.76)(8.64)(7.90)(-3.50)(-3.07)(-3.31)(-2.94)30.6218***0.5354***0.4829***0.4750***0.4357***-0.1861**-0.1852***-0.1844***-0.1764**(3.61)(7.53)(6.94)(5.02)(6.32)(-4.33)(-4.47)(-4.15)(-3.77)

3.5.3明星分析师荐股评级调整与市场过度

反应

Mikhail等[40]和Ivkoviĉ等[41]考察了分析师评级调整对过度反应的影响.为了给出稳健性检验，本文进一步考察明星分析师评级调整对动量效应、反转效应的影响.由于分析师较少地下调评级，且评级在3以上的报告也较少(45 039份荐股报告中仅有2 444份评级等于或高于3.按月统计结果显示，各月样本中评级结果等于或高于3的样本占比最多的为20%，平均值为1.2%，75%分位数为1.1%.).因此，该部分检验使用的样本仅限于上调评级且上调后评级结果小于或等于3的报告.具体的检验步骤为：

1)对各月的股票计算t-12至t-2期的持有期收益率，并根据分位数将股票分为5个Mom组，Mom1组股票在过去的收益率表现最差，Mom5组在过去的表现最好.

2)将每个Mom组中股票按分析师类别分为明星、非明星分析师组.

3)对于每个Analyst-Mom组，计算t月、t～t+3月以及t～t+11月的算术平均值，以及Mom5组和Mom1组收益率之差的总市值加权平均值*在这里使用t～t+3和t～t+11月，而没有采用之前使用的t～t+5、t～t+11月和 t+12～ t+35月.这是因为分析师通常在股市收益率上涨(或下跌)一段时间后才做出上调(或下降)评级预测，而本文设定发布评级调整当月为t月，此时股价已经上涨(或下跌)了一定时间，因此将反转效应的计算时期缩短了..

4)从2004年1月到2013年12月，计算上述各月结果的时间序列平均值，及相应的t统计量.

动量效应(第t月平均收益率)的结果列在表11中，明星分析师评级调整引起的动量效应在10%水平下显著为0.84%，而非明星分析师组的动量效应不显著.这一结果稳健地支持了本文的假设2a.

反转效应(第t至t+3及第t至t+11月平均收益率)的结果列在表12中，结果同样表明明星分析师荐股调整与反转效应具有显著的正相关关系，而非明星分析师组与反转效应不存在显著的关系.这一结果同样稳健地支持了本文的假设4b.

表11　明星分析师、正向评级变动与股价的动量效应

表12明星分析师、正向评级变动与股价的反转效应

Table 12 Star analysts, bullish recommendations, and reversal effects

Panel A:t～t+3月

Panel A:t～t+3 month

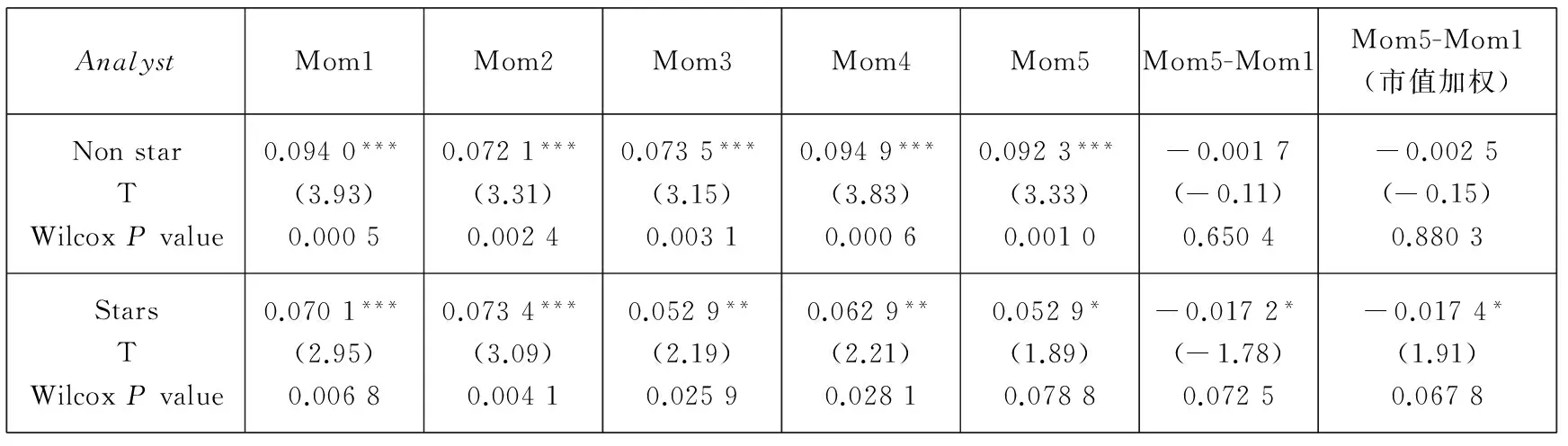
AnalystMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(市值加权)NonstarTWilcoxPvalue0.0940***(3.93)0.00050.0721***(3.31)0.00240.0735***(3.15)0.00310.0949***(3.83)0.00060.0923***(3.33)0.0010-0.0017(-0.11)0.6504-0.0025(-0.15)0.8803StarsTWilcoxPvalue0.0701***(2.95)0.00680.0734***(3.09)0.00410.0529**(2.19)0.02590.0629**(2.21)0.02810.0529*(1.89)0.0788-0.0172*(-1.78)0.0725-0.0174*(1.91)0.0678

Panel B:t～t+11 月

Panel B:t～t+11 month

AnalystMom1Mom2Mom3Mom4Mom5Mom5-Mom1Mom5-Mom1(市值加权)NonstarTWilcoxPvalue0.1249***(4.14)0.00020.0924***(3.64)0.00100.0894***(3.33)0.00210.1143***(3.85)0.00030.1149***(3.37)0.0014-0.0101*(1.80)0.0899-0.0110**(-2.04)0.0372StarsTWilcoxPvalue0.0942***(3.21)0.00270.0973***(3.17)0.00370.0759**(2.62)0.01680.0877**(2.57)0.01090.0731**(2.25)0.0355-0.0211**(-2.73)0.0138-0.0218**(-2.11)0.0405

3.5.4明星分析师评级调整与异常成交额

市场的过度反应除了会反映在股价变化上，也会反应在成交额的变化上.为了考察明星分析师评级调整引起的异常成交额，本文将评级调整报告分为明星、非明星分析师两组，根据模型(2)分别计算各组分析师做出调整后第1、5、11、35月的异常成交额，然后从2004年1月到2013年12月计算各组结果的平均值，算术平均值列在表13的Panel A中，总市值加权平均值列在表13的Panel B中.

Panel A的结果显示，明星分析师做出盈余调整后，在第1月中异常成交额为1.201 3，而非明星分析师组该数据为1.128 0，t检验表明两者在5%水平下具有显著差异.这一结果表明，明星分析师评级调整与异常成交额之间存在着显著的正相关关系，且这一关系强于非明星分析师.表13中其他各期结果和加权计算结果与之相似.总之，这些结果支持了本文的假设4c.

表13明星分析师与异常成交额

Table 13 Star analyst and abnormal volume

首先，逐年逐月将评级调整报告按分析师声誉分为两组，对每组报告涉及的股票，根据模型(2)计算评级调整报告发布后M月的异常成交额.各组—期(Analyst-Period)异常成交额的算术平均值及总市值加权平均值分别列在Panel A和Panel B中，相应的t统计量在括号里，第三行给出明星、非明星两组异常成交额的t检验的P值.

Panel A: 算术平均值

Panel A: Arithmetic mean

StarFgroupM=1M=5M=11M=23Nonstar1.1280***1.0854***1.1763***1.0820***(32.14)(104.81)(87.31)(112.79)Star1.2013***(75.37)1.0909***(42.57)1.2097***(38.20)1.0947***(45.03)Pvalue0.01740.09370.00010.1652

Panel B: 总市值加权平均值

Panel B: Market value-weighted mean

StarFgroupM=1M=5M=11M=23Nonstar1.1078***1.0867***1.1950***1.1072***(33.65)(90.86)(92.77)(100.57)Star1.1160***1.1159***1.2253***1.1084***(49.21)(37.62)(37.86)(27.12)Pvalue0.01650.09780.00450.2756

3.6明星、非明星分析师与市场过度反应： 稳健

性检验

本文还给出了使用Fama-MacBeth回归方法对明星分析师与动量效应及反转效应联系的检验.使用Fama-MacBeth[42]回归方法的优势在于1)回归方程允许考虑更多的控制变量，从而使结果更为稳健；2)截面回归赋予估计结果不同的权重，这为本文提供了更多不同权重下的估计结果.具体实证方法如下：首先，从2006年6月到2013年12月，每月对模型(8)做横截面OLS估计；然后，计算估计系数每月的平均值，以及相应的t统计量.模型(8)如下

Reti,t=α0+β1Reti,t(-12∶ -2)+

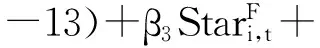
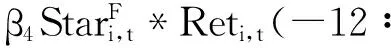
(8)其中Ret为股票月度收益率，Control包括上月收益率Ret(-1:-1)*Jegadeesh[30]、以及鲁臻等[31]的研究结果都表明，短期反转效应对股票收益率具有显著影响.因此，本文将上月收益率作为控制变量.、LnSize以及LnBM.根据Petersen[32]，上述模型中的估计系数的标准差经过Newey-West修正.

在模型(8)中，解释变量包括：1)Ret(-12∶-2)，可以考察短期动量效应；2)Ret(-36∶-13)，可以考察中长期反转效应；3)StarF，可以考察明星分析师给股价带来的影响；4)StarF与Ret(-12∶-2)的交叉项，可以考察明星分析师跟踪人数与短期动量效应之间的关系；5)StarF与Ret(-36∶-13)的交叉项，可以考察明星分析师跟踪人数与中长期反转效应之间的关系.

模型(8)的估计结果列在表14的Panel A中.第(1)列中Ret(-12∶-2)和Ret(-36∶-13)的估计系数分别显著为正和显著为负，说明股票存在着显著的短期动量效应、以及中期和长期反转效应.第(2)列的检验结果表明明星分析师跟踪与股票收益率具有正向关系，这与Fang 等[5]、Stickel[22]等研究结果相似.第(3)列加入了StarF与Ret(-12∶-2)的交叉项，其估计系数在10%水平下显著为正，说明明星分析师跟踪人数越多的股票，其短期的动量效应越强.第(4)列给出了StarF与Ret(-36∶-13)交叉项的估计结果，其结果表明，两者存在着显著为负的相关关系，说明对于明星分析师跟踪人数越高的股票，其长期的反转效应也越强.第(5)列同时包含了上述两种交叉项时，其结果均显著，且与上述结果保持一致的正负关系.因此，本文对模型(8)进行的回归分析也支持了本文的明星分析师引起更大程度过度反应的假设.

在Panel B中，本文将模型(8)中的明星分析师跟踪人数换成非明星分析师跟踪人数，以检验非明星分析师与动量效应和反转效应的关系.从结果中可知，非明星分析师引起一定的动量效应，但是从经济意义上看没有明星分析师引起的动量效应显著.而非明星分析师与反转效应没有关系.综合来看，非明星分析师没有能引起足够的市场过度反应，这支持了本文的假设.

表14明星分析师、非明星分析师与股价动量、反转效应： Fama-MacBeth回归

Table 14 Fama-MacBeth regression results for star and non-star analysts, momentum and reversal effect

Panel A：明星分析师

Panel A: Star analysts

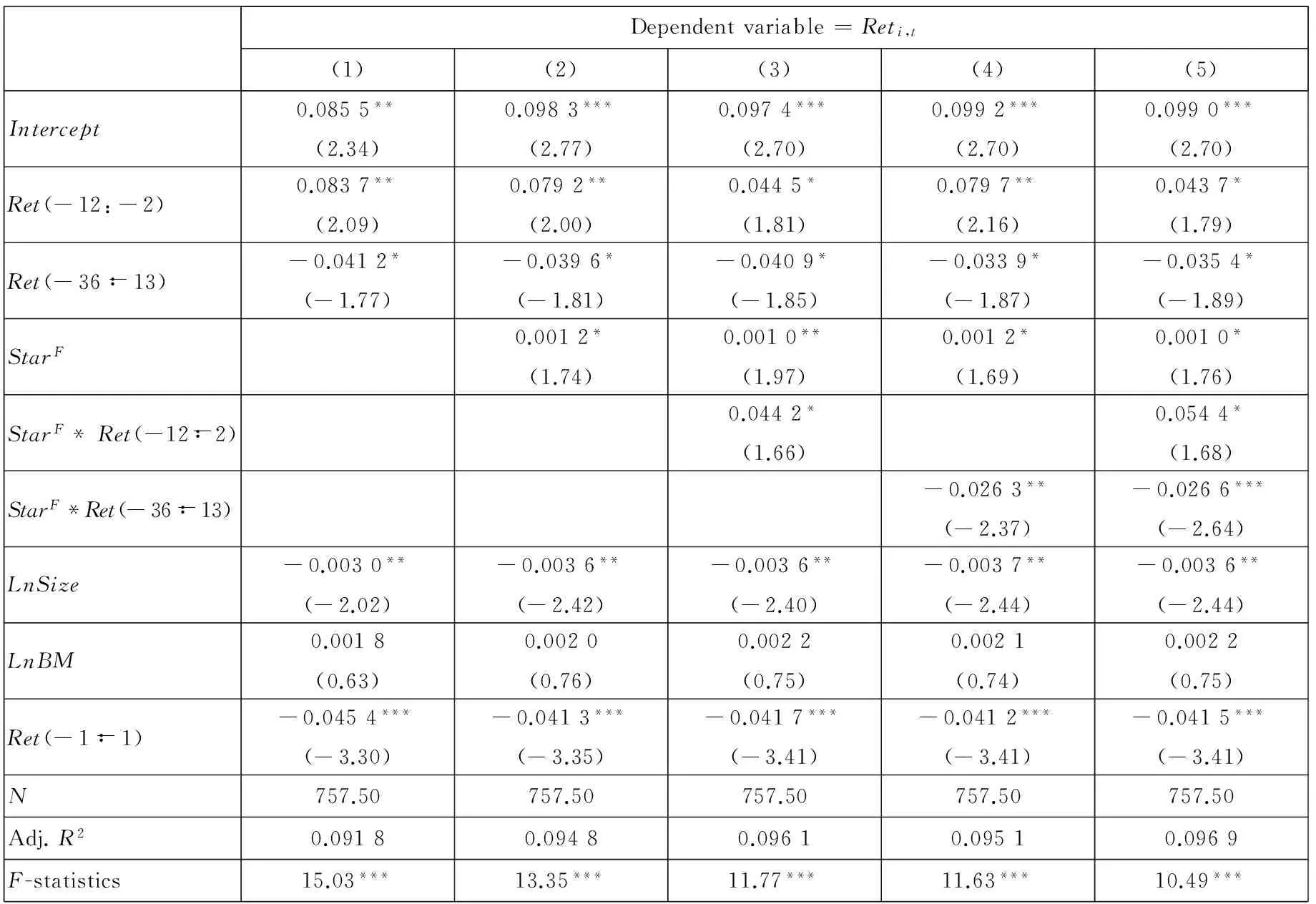
Dependentvariable=Reti,t(1)(2)(3)(4)(5)Intercept0.0855**(2.34)0.0983***(2.77)0.0974***(2.70)0.0992***(2.70)0.0990***(2.70)Ret(-12:-2)0.0837**(2.09)0.0792**(2.00)0.0445*(1.81)0.0797**(2.16)0.0437*(1.79)Ret(-36∶-13)-0.0412*(-1.77)-0.0396*(-1.81)-0.0409*(-1.85)-0.0339*(-1.87)-0.0354*(-1.89)StarF0.0012*(1.74)0.0010**(1.97)0.0012*(1.69)0.0010*(1.76)StarF*Ret(-12∶-2)0.0442*(1.66)0.0544*(1.68)StarF*Ret(-36∶-13)-0.0263**(-2.37)-0.0266***(-2.64)LnSize-0.0030**(-2.02)-0.0036**(-2.42)-0.0036**(-2.40)-0.0037**(-2.44)-0.0036**(-2.44)LnBM0.0018(0.63)0.0020(0.76)0.0022(0.75)0.0021(0.74)0.0022(0.75)Ret(-1∶-1)-0.0454***(-3.30)-0.0413***(-3.35)-0.0417***(-3.41)-0.0412***(-3.41)-0.0415***(-3.41)N757.50757.50757.50757.50757.50Adj.R20.09180.09480.09610.09510.0969F-statistics15.03***13.35***11.77***11.63***10.49***

估计系数的标准误经过Newey-West修正

Panel B： 非明星分析师

Panel B: Non-star analysts

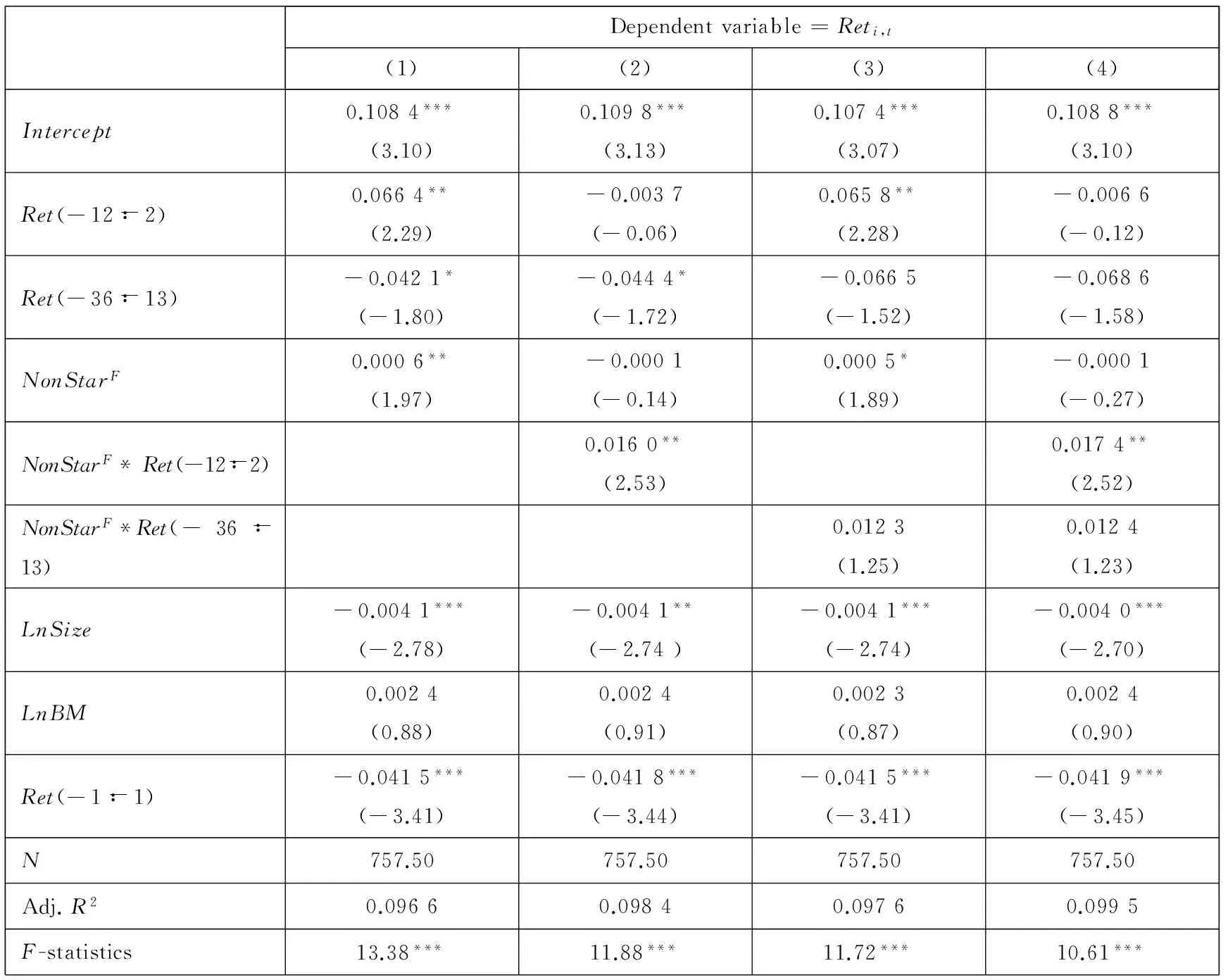
Dependentvariable=Reti,t(1)(2)(3)(4)Intercept0.1084***(3.10)0.1098***(3.13)0.1074***(3.07)0.1088***(3.10)Ret(-12∶-2)0.0664**(2.29)-0.0037(-0.06)0.0658**(2.28)-0.0066(-0.12)Ret(-36∶-13)-0.0421*(-1.80)-0.0444*(-1.72)-0.0665(-1.52)-0.0686(-1.58)NonStarF0.0006**(1.97)-0.0001(-0.14)0.0005*(1.89)-0.0001(-0.27)NonStarF*Ret(-12∶-2)0.0160**(2.53)0.0174**(2.52)NonStarF*Ret(-36∶-13)0.0123(1.25)0.0124(1.23)LnSize-0.0041***(-2.78)-0.0041**(-2.74)-0.0041***(-2.74)-0.0040***(-2.70)LnBM0.0024(0.88)0.0024(0.91)0.0023(0.87)0.0024(0.90)Ret(-1∶-1)-0.0415***(-3.41)-0.0418***(-3.44)-0.0415***(-3.41)-0.0419***(-3.45)N757.50757.50757.50757.50Adj.R20.09660.09840.09760.0995F-statistics13.38***11.88***11.72***10.61***

估计系数的标准误经过Newey-West修正

明星分析师与动量效应和反转效应的关系同样受内生性问题的干扰，假如股票由于某种未知因素使得市场对其具有过度反应，而明星分析师出于某种动机倾向于跟踪这类股票，那么市场过度反应就并非明星分析师所引起.为了减轻内生性问题带来的干扰，本文同样使用预期明星分析师跟踪人数和波动率作为工具变量，使用2SLS回归来解决内生性问题.具体方法是

1)从2006年6月到2013年12月，每月在第一阶段做以下模型估计

Stari,t=α0+θ1expStari,t+θ2Volatilityi,t+

β1Reti,t(-12∶-2)+β2Reti,t

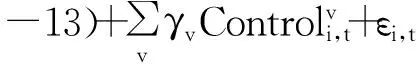
(9)

其中控制变量包括Control上月收益率Ret(-1∶-1)、LnSize以及LnBM.

2)在第二阶段中，使用上述模型得到明星分析师跟踪人数的预测值，每月对模型(8)做横截面OLS估计.然后，计算第一阶段和第二阶段估计系数每月的平均值，以及相应的t统计量.第二阶段估计系数的标准差经过Newey-West修正.结果列在表15中.

从表15可知，在修正了内生性问题后，本文的假设依然得到支持.

综合上述结论，本文假设2b被证实，即明星分析师降低股价同步性的机制并非提供更多公司层面信息，而是其他机制所导致.本文假设4的证实则表明明星分析师降低股价同步性的机制是引起市场过度反应.这一结论是稳健的，无论使用分组检验还是回归分析，无论是动量、反转效应还是异常成交额，无论使用盈余预测报告还是荐股报告，即使在修正内生性问题后，明星分析师引起市场过度反应的假设都被稳健地证实.

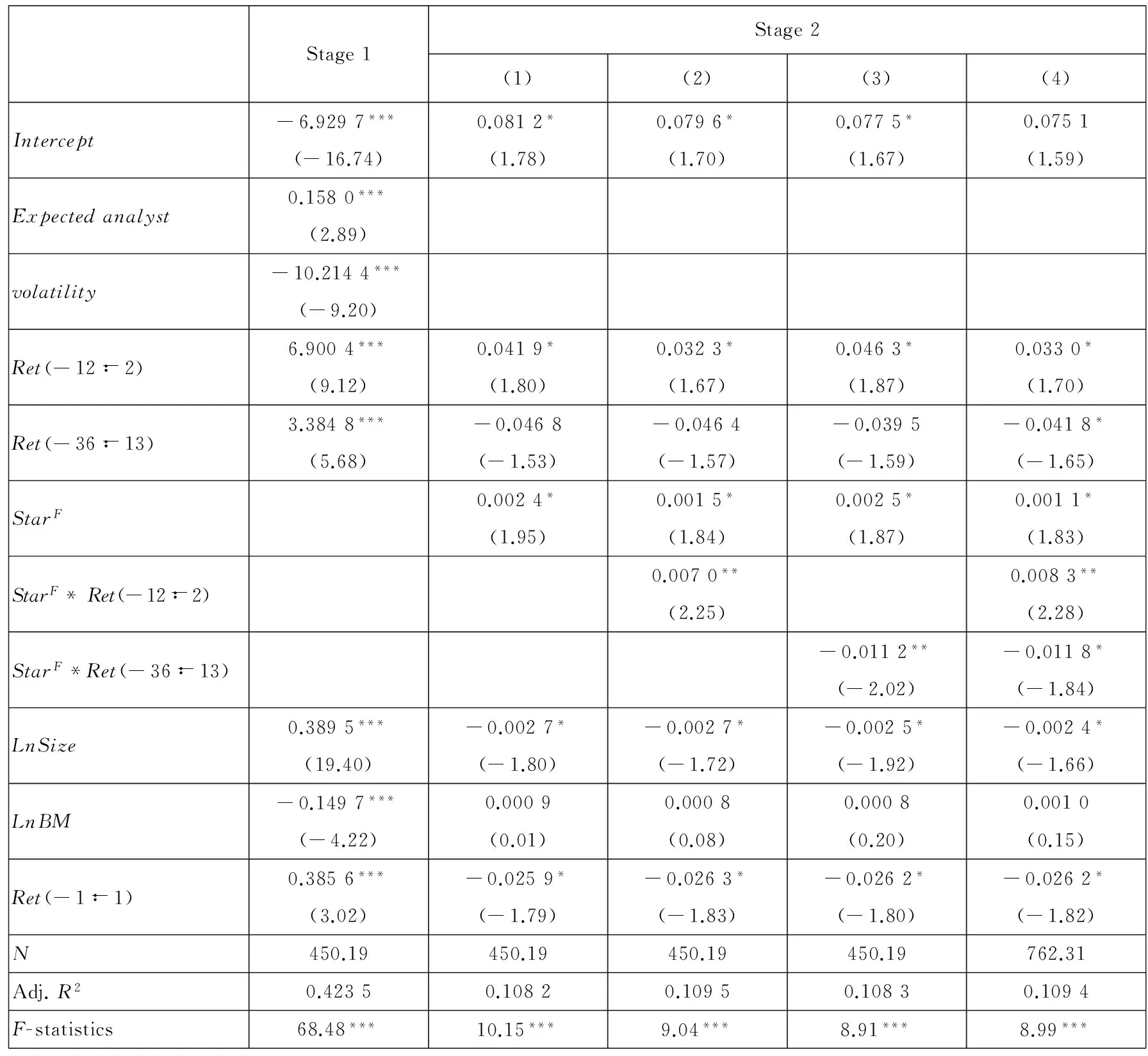
表15　明星分析师与股价动量、反转效应： 2SLS和Fama-MacBeth回归

估计系数的标准误经过Newey-West修正

4　结束语

本文重新检验了我国股票市场中明星分析师的作用.根据Hou等[3]提出的论据，本文发现明星分析师能够引起投资者的过度反应，从而能够降低股价同步性.具体发现包括：(1)对于明星分析师对股价同步性具有负向影响；(2)即使明星、非明星分析师具有相似的预测准确度，明星分析师跟踪人数仍然对股价同步性具有负向影响，而非明星分析师对股价同步性的影响不显著；(3)预测准确度最高组和最低组明星分析师跟踪股票的平均股价同步性没有显著的差异;(4)明星分析师跟踪人数以及正向的股价评级调整均能够引起更强的短期动量效应、长期反转效应和异常成交额.这些结果意味着明星分析师的信息提供作用并非是降低股价同步性的主要因素，相反，明星分析师主要通过引起市场过度反应降低股价同步性.

本文的研究发现对于认识分析师在我国证券市场中的作用以及R2的生成机理具有重要的理论与现实意义.首先，对于分析师在证券市场中的作用，以前的研究更多着眼于分析师信息提供的差异及其来源，没有考虑市场投资者对于分析师报告的信息接受和反应方式，本文拓展了已有的研究，有助于更加全面的认识明星分析师与非明星分析师在证券市场中的作用.本文的研究结果表明，为了提高我国新兴证券市场的效率，需要加强对投资者的教育以提高其成熟度，只是依赖于分析师的信息揭示作用并不能有效提高市场的定价效率.其次，对于R2生成机理的不同理论解释，本文为基于行为金融的解释提供了来自新兴证券市场新的证据.这表明，对于R2生成机理的研究有必要考虑和区分不同市场特征，从而为有关R2的未来研究提供了一定的启示和参考价值.

[1]Chan K, Hameed A. Stock price synchronicity and analyst coverage in emerging markets[J]. Journal of Financial Economics, 2006, 80(1): 115-147.

[2]Xu N, Chan K C, Jiang X, et al. Do star analysts know more firm-specific information? Evidence from China[J]. Journal of Banking and Finance, 2013, 37: 89-102.

[3]Hou K W, Peng L, Xiong W. Is R-squared a measure of market inefficiency?[R]. Princeton University Working Paper, 2013, available at: http://www.princeton.edu/～wxiong/papers/R2.pdf.

[4]Stickel S. Reputation and performance among security analysts[J]. Journal of Finance, 1992, 47(5): 1811-1836.

[5]Fang L H, Yasuda A. Are stars’ opinions worth more? The relation between analyst reputation and recommendation values[J]. Journal of Financial Services Research, 2014, 46(3): 235-269.

[6]Ashbaugh-Skaife H, Gassen J, LaFond R. Does Stock Price Synchronicity Represent Firm-specific Information? The International Evidence[R]. MIT Sloan Research Paper, No. 4551-05. Available at SSRN: http://ssrn.com/abstract=768024. 2006.

[7]Teoh S H, Yang Y G, Zhang Y. R-square and Market Efficiency[R]. Working Paper, Available at SSRN: http://ssrn.com/abstract=926948.2009.

[8]Chang E C, Luo Y. R-squared, noise, and stock returns[R]. Working Paper, 2010, Available at SSRN: http://ssrn.com/abstract=1572508.

[9]李心丹, 王冀宁, 傅浩. 中国个体证券投资者交易行为的实证研究[J]. 经济研究, 2002, (11): 54-63.

Li Xindan, Wang Jining, Fu Hao. Investigations on the transaction behaviors of Chinese individual securities investors[J].Economic Research Journal, 2002, (11): 54-63. (in Chinese)

[10]Chen G, Kim K A, Nofsinger J R. Trading performance, disposition effect, overconfidence, representativeness bias, and experience of emerging market investors[J]. Journal of Behavioral Decision Making, 2007, 20(4): 425-451.

[11]Ng L, Wu F. The trading behavior of institutions and individuals in Chinese equity markets[J]. Journal of Banking and Finance, 2007, 31(9): 2695-2710.

[12]Roll R. R2[J]. Journal of Finance, 1988, 43(2): 541-566.

[13]Morck R, Yeung B, Yu W. The information content of stock markets: Why do emerging markets have synchronous stock price movements?[J]. Journal of Financial Economics, 2000, 58(1-2): 215-260.

[14]Durnev A, Morck R, Yeung B, et al. Does greater firm-specific return variation mean more or less informed stock pricing?[J]. Journal of Accounting Research, 2003, 41(5): 797-836.

[15]Jin L, Myers S. R2 around the world: New theory and new tests[J]. Journal of Financial Economics, 2006, 79(2): 257-292.

[16]王亚平, 刘慧龙, 吴联生. 信息透明度、机构投资者与股价同步性[J]. 金融研究, 2009, (12): 162-174.

Wang Yaping, Liu Huilong, Wu Liansheng. On the information transparency, institutional investor and price comovement[J]. Journal of Financial Research, 2009, (12): 162-174. (in Chinese)

[17]潘宁宁, 朱宏泉. 基金持股与交易行为对股价联动的影响分析[J]. 管理科学学报, 2015, 18(3): 90-103.

Pan Ningning, Zhu Hongquan. Impact of fund ownership and trading on stock return synchronicity[J]. Journal of Management Sciences in China, 2015, 18(3): 90-103. (in Chinese)

[18]孔东明, 孔高文, 刘莎莎. 机构投资者、流动性与信息效率[J]. 管理科学学报, 2015, 18(3): 1-15.

Kong Dongming, Kong Gaowen, Liu Shasha. Institutional investors， liquidity， and information efficiency[J]. Journal of Management Sciences in China, 2015, 18(3): 1-15. (in Chinese)

[19]朱红军, 何贤杰, 陶林. 中国的证券分析师能够提高资本市场的效率吗——基于股价同步性和股价信息含量的经验证据[J]. 金融研究, 2007, (2): 110-121.

Zhu Hongjun, He Xianjie, Tao Lin. Can securities analysts improve the efficiency of capital market in China[J]. Journal of Financial Research, 2007, (2): 110-121. (in Chinese)

[20]周冬华, 赵玉洁. 分析师跟进能够降低审计费用吗——来自中国证券市场的经验证据[J]. 证券市场导报, 2015, (1): 13-18.

Zhou Donghua, Zhao Yujie. Can financial analysts following reduce audit fee: Empirical evidence from China[J]. Securities Market Herald, 2015, (1): 13-18. (in Chinese)

[21]Fang L H, Yasuda A. The effectiveness of reputation as a disciplinary mechanism in sell-side research[J]. Review of Financial Studies, 2009, 22(9): 3735-3777.

[22]Stickel S. The anatomy of the performance of buy and sell recommendations[J]. Financial Analysts Journal, 1995, 51(5): 25-39.

[23]Jegadeesh N, Titman S. Profitability of momentum strategies: An evaluation of alternative explanations[J]. Journal of Finance, 2001, 56(2): 699-720.

[24]Jegadeesh N, Kim W. Value of analyst recommendations: International evidence[J]. Journal of Financial Markets, 2006, 9(3): 274-309.

[25]许年行, 洪涛, 吴世农, 等. 信息传递模式、投资者心理偏差与股价“同涨同跌”现象[J]. 经济研究, 2011, (4): 135-146.

Xu Nianhang, Hong Tao, Wu Shinong, et al. Information flow model， investor psychological bias and stock price comovement[J]. Economic Research Journal, 2011, (4): 135-146. (in Chinese)

[26]Amihud Y. Illiquidity and stock returns: Cross-section and time-series effects[J]. Journal of Financial Markets, 2002, 5(1): 31-56.

[27]Gul F A, Kim J B, Qiu A A. Ownership concentration, foreign shareholding, audit quality, and stock price synchronicity: Evidence from China[J]. Journal of Financial Economics, 2010, 95(3): 425-442.

[28]Hong H, Kubik J D. Analyzing the analysts: Career concerns and biased earnings forecasts[J]. Journal of Finance, 2003, 58(1): 313-351.

[29]Piotroski J D, Roulstone R T. The influence of analysts, institutional investors, and insiders on the incorporation of market, industry, and firm-specific information into stock prices[J]. Accounting Review, 2004, 79(4): 1119-1151.

[30]Jegadeesh N. Evidence of predictable behavior of security returns[J]. Journal of Finance, 1990, 45(3): 881-898.

[31]鲁臻, 邹恒甫. 中国股市的惯性与反转效应研究[J]. 经济研究, 2007, 9(13): 145-155.

Lu Zhen, Zou Hengfu. Momentum and reversal in China stock market[J]. Economic Research Journal, 2007, 9(13): 145-155. (in Chinese)

[32]Petersen M A. Estimating standard errors in finance panel data sets: Comparing approaches[J]. Review of Financial Studies, 2009, 22(1): 435-480.

[33]Yu F. Analyst coverage and earnings management[J]. Journal of Financial Economics, 2008, 88(2): 245-271.

[34]史永东, 李凤羽. 卖空限制、意见分歧收敛与信息披露的股价效应——来自A股市场的经验证据[J]. 金融研究, 2012, (8): 111-124.

Shi Yongdong, Li Fengyu. Short-sales constraints, convergence of opinions and price effect of information disclosure: Evidence from A-share stock market in China[J]. Journal of Financial Research, 2012, (8): 111-124. (in Chinese)

[35]李冬昕, 李心丹, 俞红海, 等. 询价机构报价中的意见分歧与IPO定价机制研究[J]. 经济研究, 2014, (7): 151-164.

Li Dongxin, Li Xindan, Yu Honghai, et al. Disagreement of institutional investors’bids and IPO pricing mechanism[J]. Economic Research Journal, 2014, (7): 151-164. (in Chinese)

[36]Diether K B, Malloy C J, Scherbina A. Differences of opinion and the cross section of stock returns[J]. Journal of Finance, 2002, 57(5): 2113-2141.

[37]Ball R, Kothari S. Nonstationary expected returns: Implications for tests of market efficiency and serial correlations in returns[J]. Journal of Financial Economics, 1989, 25(1): 51-74.

[38]Zarowin P. Size, seasonality, and stock market overreaction[J]. Journal of Financial and Quantitative Analysis, 1990, 25(01): 113-125.

[39]Fama E, French K. Common risk factors in the returns on stocks and bonds[J]. Journal of Financial Economics, 1993, 33(1): 3-56.

[40]Mikhail M B, Walther B R, Willis R H. Do security analysts exhibit persistent differences in stock picking ability?[J]. Journal of Financial Economics, 2004, 74(1): 67-91.

[41]Ivkoviĉ Z, Jegadeesh N. The timing and value of forecast and recommendation revisions[J]. Journal of Financial Economics, 2004, 73(3): 443-463.

[42]Fama E, MacBeth J. Risk, return, and equilibrium: Empirical tests[J]. Journal of Political Economy, 1973, 81: 607-636.

附录1

Hou等模型和主要结论

Hout等对R2是否与市场效率相联系进行了检验.在其构建的理性预期模型中，投资者对公司信息进行理性反应，则R2与股价中包含的公司层面信息相互独立.在非理性模型中，股价受投资者情绪影响，则R2随着中期动量效应和长期反转效应的增强而降低.

1)理性预期模型

Hout等假定代表性投资对现有信息理性反应.具有风险的股票经历三期，t=0，1，2，股票在第2期产生最终收益，而收益在前两期无法被观测.收益由下列线性模型给出

f=βu+v

其中u是市场因子，v是公司特质性因子，β是因子载荷.u和v相互独立且服从高斯分布，即

u～N(0,1/τu)，v～N(0,1/τv)

在第1期，投资者观察到两个关于u和v的信号，分别是su和sv，且

su=u+εu,

sv=u+εv

其中εu和εv相互独立，且独立于u和v，并且分别服从于零均值和方差分别为1/τs,u和1/τs,v的高斯分布.那么，τs,u和τs,v则表示了被代表性投资者所接触的市场和公司层面信息.

根据贝叶斯法则，代表性投资者在第1期对u和v的后验信念也为高斯分布，且均值分别为

风险中性投资者的预期收益构成如下股票价格

p0=0，

p2=βu+v

那么在第0期到第1期之间，收益率变动被市场因素所解释的部分为

上式随着τs,v的增加为降低，即当公司层面信息增加时，第0期到第1期的R2是下降的.

但是，在3个时期中，股票收益率的波动为

上式表明无论市场还是公司层面驱动的波动都与公司层面信息τs,v无关，即

不随公司层面信息变化.

2)投资者反应偏差

假设投资者对于sv的估计存在偏差φ>0，如果φ>1，则投资者存在过度反应；如果φ<1，则投资者存在反应不足.

为了将R2和中期动量效应和长期反转效应相联系，Hou等在第1期和第2期之间加入1期，t=1.5.假设代表性投资者在第1期时对sv的评价无偏，在第1.5期根据公开消息θ更新评价.Θ以0.5的概率为1或者-1，如果θ=-1，则投资者视公开消息为噪声，坚持原来的评价.

投资者在第1期关于v的信念是

第1.5期的信念是

因此，股票价格分别为

p0=0，

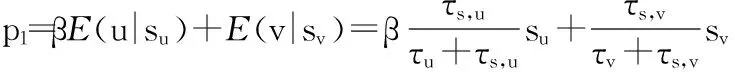
p2=βu+v

那么

其中

则

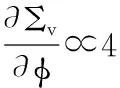
前两个区间(第0期到第1期，第1期到第1.5期)股票收益率的协方差为

Ω=cov(p1-p0,p1.5-p1)

则

如果φ>1，则Ω>0.即继续的过度反应导致前两个区间收益率存在正相关关系，即存在动量效应.当投资者在第2期修正预期后，股价回调，导致反转效应.

综上，只要投资者对公司层面信息存在持续的过度反应，则R2与中期动量效应和长期反转效应呈负相关关系.

附录2 变量设定

Appendix 2 Definition of variables

Star analyst coverage and stock price synchronicity： Empirical evidence based on market overreaction

ZHOUMing-shan1,LINJing2,XUNian-hang3

1． School of Finance, Southwestern University of Finance and Economics, Chengdu 611130, China;2． School of Economics, Peking University, Beijing 100871, China;3． School of Business, Renmin University of China, Beijing 100872, China

This paper studies how star analyst’s following decreases stock price synchronicity and argues that stars perform this function by inducing market over-reaction based on behavioral finance. The paper finds that, even if both star and non-star analysts have similar abilities (as proxied by similar earnings forecast error), star analyst’s coverage continues to be negatively related to synchronicity, while non-star analyst’s coverage does not. Secondly, the averageR2of firms followed by stars with the most accurate earnings forecasts is insignificantly different from that followed by stars with the worst accurate earnings forecasts. These results suggest that information is not the only mechanism through which stars lower price synchronicity. Finally, stars coverage and bullish recommendation revision are positively related to short-term momentum, mid-and long-term reversal and abnormal trading volume, respectively. The above results are consistent with our hypothesis. Overall, these findings help us understand the roles analysts played in emerging markets and the mechanism through which stock price synchronicity is linked to analyst’s coverage.

star analyst； market overreaction； stock price synchronicity

变量描述Rsq Rsq为以下市场模型估计的可决系数ri,w=αi,w+βi,wrm,w+γi,wrind,w+εi,wri,w股票i在w周的收益率;rm,w和rind,w分别为A股市场总市值加权平均收益率和股票i所在行业的总市值加权平均收益率.对于股票i,在计算与其对应的行业收益率时,股票i被排除在组合外,以避免结果受重复计算的影响.AnaCovF 平均分析师跟踪人数StarF 《新财富》最佳分析师Revision 同一分析师(或分析师组)对同一股票在同一年份中两次荐股评级得分之差,小于0表示上调评级,等于0表示维持上次评级结果.StdRec 标准化评级,取值从1到5,分别代表“买入”,“增持”,“中性”,“减持”,“卖出.Ret(%)月度股票收益率Top1第一大股东持股比例GovHold国有股占比InsHold机构投资者持股比例Turnover年成交额除以年末总市值LnSize总市值的自然对数形式MB市值账面比IndNum行业中公司总数LnIndSize行业中所有公司总市值之和的自然对数形式Ret(-12∶-2)第t-12tot-2月持有期收益率Ret(-36∶-13)第t-36tot-13月持有期收益率LnBM账面市值比的自然对数形式Ret(-1∶-1)上月末收益率FEFEj,i,y=|F_EPSj,i,y-EPSi,y|Pricei,y其中F_EPSj,i,y为第j个分析师对股票i在第y年做出的盈余预测值;EPSi,y为股票i在第y年的真实盈余;Pricei,y股票i在第y年的收盘价.AVoli,tAVoli,t=∑Mt=1Volumei,t/M∑M+12t=-24Volumei,t/(M+36)其中Volume为月成交额;M为月数.

① 2015-06-29；

2016-04-18.

国家自然科学基金资助项目(71572151).

周铭山(1976—)， 男， 江西广丰人， 博士， 副教授. Email： zhoumingshan@swufe.edu.cn

F832.5

A

1007-9807(2016)06-0049-25