具有技术转让的捆绑采购最优决策研究①

魏　航， 谈　丹， 李　佩

(上海财经大学国际工商管理学院， 上海 200433)



具有技术转让的捆绑采购最优决策研究①

魏航， 谈丹， 李佩

(上海财经大学国际工商管理学院， 上海 200433)

为了获取先进的技术，采购方通常采用将产品和技术进行捆绑采购的采购策略.不同的供应商有着不同的技术优势，采购方可以在不同供应商之间分配采购量来获得拥有不同技术优势供应商的技术，并加以组合吸收以提高自身技术水平.基于此，研究了具有技术转让的捆绑采购最优决策问题，通过对采购方利用供应商之间技术的互补性而采取的组合捆绑采购策略的描述，用经典的消费者效用函数构建了采购方进行捆绑采购的效用，并结合随机效用理论建立了离散选择模型研究了技术捆绑采购过程中最优采购量、最优分配比例问题，给出了单变量决策中的最优采购量和最优分配比例，并进一步研究了最优采购量和最优分配比例的双变量决策问题，给出了最优双变量组合决策和条件.最后，给出了一个算例，并进行了敏感性分析.

技术转让； 捆绑； MNL模型； 采购量； 分配比例

0　引　言

在过去的三十年里，中国通过改革开放获得了空前的经济增长.然而，随着中国劳动力价格上升，人口红利降低，中国企业为了加快产业升级和提升国内乃至国际市场的竞争力，迫切需要获得先进的技术.改革开放后尤其是1990年后，我国进入技术引进的全方位发展时期，在能源、机电、石化、有色金属、邮电交通等领域与外国公司展开了全面的技术合作.据统计，迄今为止我国共引进技术8万项，合同金额超过2千亿美金.在引进先进技术与装备的基础上，逐步消化、吸收，最后再进行相应的自主创新，使得我国工业特别是装备制造业的产业规模、产品质量乃至技术水平方面都获得了显著提高，同时，也为我国民族企业提供了进入某些高技术产业的途径.

在推动产业的现代化升级过程中，中国政府始终发挥着主导作用，期望通过法律和技术的引进来完成产业的升级和企业技术水平的提升.目前，中国政府往往通过同时采购所需的项目产品和内在技术的捆绑采购策略获得技术.这意味着为了获得项目合同，供应商需要承诺将项目产品的技术转让给中国企业.中国企业通过这种方式获得技术，经过消化、吸收后，将在未来市场上成为新的供应商.比如：①举世瞩目的三峡水电工程中，第一批三峡左岸电站的14台机组由德国伏伊特(VOITH)公司、美国通用电气(GE)公司、德国西门子(SIEMENS)公司组成的VGS联营体和法国阿尔斯通(ALSTOM)公司、瑞士ABB公司组成的ALSTOM联营体共同赢得了竞标，中国企业也从此次交易中获取了水电站机组技术并在世界范围内参与竞争*资料来源： http://news.sina.com.cn/c/2003-09-25/1653819712s.shtml..②中国国家高速铁路系统项目，其主要引进了法国阿尔斯通、德国西门子、加拿大庞巴迪和日本川崎重工的高铁技术，并在此基础上吸收4家之精华，自主研制出时速在350 km左右的高速列车，居世界领先地位.中国高铁目前在工务工程技术、列车制造技术、列车控制系统、系统集成技术等方面都已经走在国际前列，并逐渐开始向其他国家出口*资料来源： http://www.changjiangtimes.com/2014/12/494653.html..

随着中国经济的不断增长以及潜在市场规模的不断扩大，西方国家逐步开始放开对中国的技术封锁.相应的，中国政府和企业在进行技术引进时所面对的问题，也由如何找到愿意出售技术的卖方，逐渐转变为当同时引进多种技术时如何决策不同供应商的采购量，获得不同的技术水平，以有利于未来自主研发生产同类具有竞争力的产品.这种相比于过去仅仅是单一地采购产品或技术的情况，有着很大的区别.因此，企业在进行产品与技术捆绑采购时，需要根据自身产品的需求、未来市场情况、不同产品供应商的技术水平和优势等情况，确定产品的采购量和不同供应商之间的分配情况，以获得对自身最优的资源与技术.

对于具有技术转让的捆绑采购最优决策问题，这里的决策包括产品采购量决策和采购量分配决策，其中研究内容主要涉及捆绑理论与技术转让等方面，下面将按照这两个方面来阐述文献综述.

捆绑销售是以特殊价格整体销售两种及更多产品和服务[1]，主要分为纯捆绑(pure bundling)和混合捆绑(mixed bundling)[2].对于捆绑销售的理论研究最早出现在经济学领域，主要包括垄断者的最优捆绑决策[2-3]、捆绑的均衡理论[4，5]及捆绑的福利分析[6].近年来管理科学领域对捆绑销售的研究越来越多，主要集中在对捆绑策略的研究.Bakos和Brynjolfsson[7]发现捆绑大量不相关的信息产品能获得较高利润.Guiltinan[1]提出了为不同的混合捆绑折扣形式选择合适类型服务的规范体系.彭赓等[8]认为只要把大量的信息产品捆绑在一起进行销售，就能够有效地降低消费者对于商品估价的差异.吕魁等[9]研究了范围经济和转换成本对网络产业中多产品捆绑销售竞争均衡的影响.除此之外，还有大量对捆绑销售定价的研究.Hanson和Martin[10]利用混合整数规划来求解，并将该捆绑价格模型应用于产品线产品的选择上.Mulhern和Leone[11]提出了零售业相关商品捆绑销售的定价和促销政策的理论框架.Johnson等[12]等则从相反的角度来讨论捆绑销售策略，他们认为通过将产品进行捆绑销售，会改变消费者对产品的感知价值.

对于技术转让的研究，根据联合国《国际技术转让行动守则草案》的定义，技术转让是指关于制造产品、应用生产方法或提供服务的系统知识的转让，但不包括贸易的单纯买卖或租赁.近年来，国内外学者主要对技术转让的性质、策略、转让方式等进行研究.Schmitz[13]分析了当市场上存在一个垄断的研究型企业和两个生产型企业时技术转让的策略性问题，结果表明研究型企业对两个生产型企业都进行技术许可，可以规避因私人信息带来的利润损失.Yi[14]的研究表明当一个有技术优势的企业面对两个开发替代技术但当前仍处于技术劣势的企业时，若替代性的模仿技术被开发出来，则对技术优势企业而言，对其中实力较强的企业进行排他性技术许可是最优的.Chu和Wang[15]研究了在技术产品采购的公开市场招标情况下，未来市场规模与当前市场规模的比率对于技术转让中技术水平的影响，研究表明当这一比率等于或大于10%时，供应商愿意提供全部的技术水平.田晓丽和付红艳[16]基于双寡头古诺竞争模型，探讨了非生产性研发企业在技术授权与纵向兼并这两种技术传播途径之间的选择及其福利效应.

随着经济的发展和产业的现代化升级，中国重大技术引进的方式和策略也成为学术界关注的焦点之一.由于在对飞机、火车、核电站等重大技术引进时，采购的主体大多为国家和企业等离散的个体，并且供应商所拥有的技术水平也不尽相同，因此如何确定产品的采购量和不同供应商之间的分配情况成为亟需解决的问题.基于此，本文研究了具有技术转让的捆绑采购最优决策问题，通过对采购方利用供应商之间技术的互补性而采取的组合捆绑采购策略的描述，用经典的消费者效用函数(柯布-道格拉斯函数)来构建采购方进行捆绑采购的效用，并结合随机效用理论建立了离散选择模型(MNL模型)来研究技术捆绑采购过程中的最优采购量、最优分配比例问题，给出了单变量决策中的最优采购量和最优分配比例，并进一步研究了最优采购量和最优分配比例的双变量决策问题，为未来国家进行重大技术引进提供一定的参考.

1　模型的基本设定

1.1交易机制与过程描述

在某个技术含量较高的产品市场(如飞机、高铁机车等)，采购方想要获得潜在的技术，并同当前市场已存在的供应商在未来市场上竞争.一种常见的方法是，采购方同供应商谈判，以一定的价格采购某个数量的产品，并借此对产品中所含技术进行消化、吸收，以在未来市场上形成竞争能力.在现实的经济生活中，技术产品市场往往是寡头垄断市场，即存在多个供应商，每个供应商的产品在某方面的技术会有其特殊的优势.因此，技术采购方在技术引进阶段往往也是对供应商各方面技术进行综合比较后选择自己所需要的技术签订捆绑合同.例如，在中国高铁采购的过程中，中方通过同德国西门子集团的交易获得了信号控制、牵引控制系统、列车网络控制系统等技术，而同日本川崎重工的合作中，中方获得了生产高速机车组的相应技术.

假设当前市场上存在两个供应商，并且不同供应商产品的技术是异质的，如果采购方能同时获得这两种技术，则会产生某种组合效应，形象的说就是产生一加一大于二的效果.在此过程中，采购方需要决策：捆绑采购如何在两个供应商之间进行分配？最优采购量和分配比例是多少？具体的交易过程与机制可以用图1来说明.

图1交易机制和问题描述

Fig.1 Transaction mechanism and the problem description

阶段1(技术引进阶段)

市场上存在一个采购方(购买者)和两个供应商(供应商 1，供应商 2)，采购方所需要采购一定数量的产品，其中，一部分产品向供应商 1采购，获取产品中所含的部分技术，剩余部分产品向供应商 2采购，并获取另一部分技术.

阶段2(技术消化吸收阶段)

采购方对获取的两种技术进行消化、吸收.

阶段3(技术投产收益阶段)

采购方(可以看为供应商0)掌握了两种技术后，同原本存在的供应商 1和供应商 2共同在市场上竞争*在阶段3，采购方掌握了技术并参与到供应商的竞争，因此可以把采购方看作供应商0..

1.2符号描述

首先，对本文中所涉及的参数和决策变量的符号进行定义：

参数符号

π0表示捆绑采购时采取技术捆绑时采购方的收益；

(ti1，ti2)表示供应商i在市场上提供产品的技术水平组合，i=1,2；

pi表示供应商i在进行技术转让时的单位产品价格，i=1,2；

ci表示供应商i生产单位产品的成本，i=0,1,2；

a表示采购量的增加对供应商愿意转让的技术水平的影响参数，且a>0；

qi表示在阶段3消费者选择采购供应商i产品的概率，或者说是供应商i在阶段3的市场份额⑥对于某个特定的采购者来说，qi表示在阶段3其选择采购供应商i产品的概率.当拓展到整个市场上的众多消费者时，qi就可以看作是供应商i产品所占有的市场份额.，i=0,1,2；

M表示采购方在阶段1所能采购的最大产品量(假设该M是一个足够大的值)；

l表示阶段3市场对于产品的总需求量；

Vi(m，β)表示供应商i在阶段3所能获得的收益，i=0,1,2.

决策变量

m表示采购方在阶段1采购的产品总量；

β表示采购方向供应商1采购产品的分配比例.

1.3关于技术的假设

假设1假设对于所交易的产品主要涉及两部分技术，例如在动车市场上包含火车机车组技术和轨道技术.因此，对于某一供应商i，其所提供的产品的技术水平组合可用(ti1，ti2)来表示，分别表示产品两方面的技术水平.

假设2假设在任何一个技术维度上，供应商愿意提供的技术水平与当前采购方的采购量的比率成正相关关系[15].即当采购方从供应商i处采购m件技术含量为(ti1，ti2)的产品后，其所能吸收获得的技术水平为 ((1-e-am)ti1，(1-e-am)ti2).

假设3假设供应商1 和 2分别在第1和第2项技术领域具有较大的优势，并且采购方在签订捆绑合同时所涉及的技术引进只针对其优势技术，因此采购方通过技术组合捆绑采购所获得的技术水平为 ((1-e-αβm)t11，(1-e-a(1-β)m)t22).

1.4阶段3客户选择的MNL模型

现代经济学选择理论认为消费者按照偏好最大化的要求实施市场行为，偏好是由感知、态度和其它难以测量的因素的变动所产生的随机成分组成的.现有考虑消费者效用的需求函数主要包括两类：一类是假设消费者是不同质且是连续分布的，通过不同消费者对相同产品的不同偏好来确定需求；另一类是通过离散选择模型分析消费者对不同产品的选择来确定需求，例如McFadden在以往研究的基础上提出了随机效用理论的离散选择模型，即多项式logit模型(multinomial logit model，MNL)[17].对于采购方来说，在阶段3市场有3个供应商(采购方和两家供应商)，各供应商的产品价格、技术水平也不完全相同，技术采购方的销售收益则由消费者对产品的选择决定.考虑到进行大型技术设备采购的消费主体大多是非连续的个体，并且可供消费者选择的产品也并非完全同质，因此，本文利用MNL 模型对采购方在阶段3参与市场竞争时的效用进行度量，以获得消费者选择其产品的概率.根据以上MNL基本模型的结论，现在加入如下假设，以便在本文中拓展运用：

假设1产品效用的确定部分由产品所含的技术水平决定，在此假设对于某一高科技产品的确定效用采购方是通过两方面的技术水平来衡量的，即

u=u(ti1，ti2)

同时假设消费者对于这两部分技术的偏好是凸的，即对于任意两种技术组合的产品(ti1，ti2)和(ti3，ti4)来说，总有以下不等式成立

一种典型的凸偏好效用函数是柯布-道格拉斯效用函数：u(ti1，ti2)=ti1bti2c，在此利用这种形式，并假设消费者对于这两部分技术的偏好相同，即b=c=1，如图2所示.

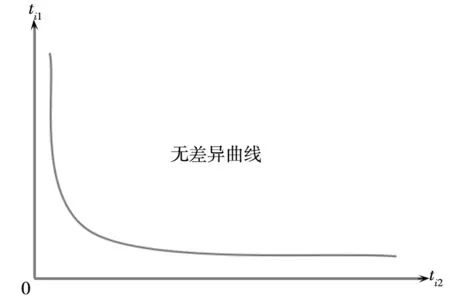
图2　消费者无差异曲线关系

假设2

消费者在选择产品时，其总体效用中还包含价格因素，即

Uj=uj-pj+εj

根据以上两个假设，消费者选择产品j的概率可以拓展为

将uj=u(tj1，tj2)=tj1tj2代入上式则有

2　收益与市场份额分析

2.1收益分析

根据给出的关于技术组合产品采购的描述，对于某一种给定的组合，其采购的产品总量以及对每个供应商的采购量分别为：采购方在阶段1共采购m单位数量的产品，其中，βm(0≤β≤1)向供应商1采购，(1-β)m向供应商2采购.这样，在阶段3，市场上所出现的可供消费者选择的产品的技术和价格组合就有三种，见表1*需要注意的是阶段3的消费者只需要采购技术产品本身而不需要捆绑采购技术..

表1　阶段3市场可供选择的产品

这样，在阶段3市场上顾客选择采购方产品的概率(或者说是采购方的市场份额)即可表示为

q0=

(1)

同时，大型装备制造业的需求主体大多相对固定，通过专业的需求调研和预测可以减少未来需求的不确定性.因此假设阶段3市场对于产品的总需求为确定的l，进一步，采购方3个阶段的全部收益即为

π0=βm(t11t12-p1)+(1-β)m(t21t22-p2)+

V0(m，β)

(2)

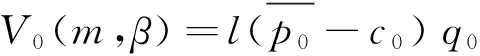
2.2未来市场份额

根据前文所述，q0表示在阶段3消费者选择采购第1阶段的采购方提供的产品的概率，这包含两层含义：1)当阶段3只存在一个消费者时，q0表示该消费者选择采购采购方产品的概率；2)当阶段3存在多个消费者时，q0则表示选择第1阶段的采购方产品的消费者占全部消费者的百分比，即市场份额.

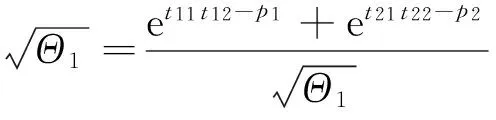
其中 Θ1=

证明

q0(m)对m求导得

因为0≤β≤1，可得

aβe-aβm+a(1-β)e-a(1-β)m-ae-am≥

aβe-am+a(1-β)e-am-ae-am=0

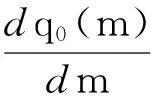
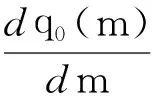
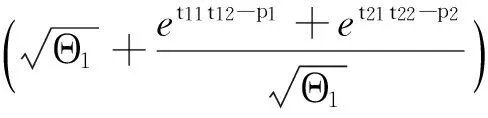
证毕.

证明q0(β)关于β求导并使其值为0可得

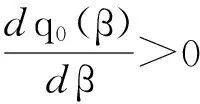
(4)

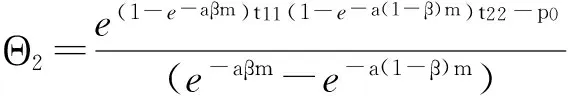
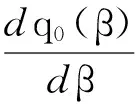
证毕.

3　最优采购量和最优分配比例决策

当采购方确定采取技术捆绑采购，则采购量m和分配比例β都是需要考虑并决策的重要问题，他们共同影响着采购方三个阶段的总收益，下面先分别考虑两个变量的单变量决策问题，再综合讨论双变量决策问题.

3.1最优采购量决策

假设分配比例β已经确定，则如何确定采购量m成为采购方决策的重要问题，它将直接影响采购方3阶段的总收益.根据组合采购的收益分析，计算最优分配采购量m*.

定理3当采购方在阶段1产品采购量分配比例为β时，存在唯一的最优采购量m*，采购方根据阶段1的单位产品收益*由于分配比例确定，即相当于每单位产品都由两位供应商各自提供一部分，β(t11t12-p1)+(1-β)(t21t22-p2)就表示这种情况下采购者在阶段1从每单位购得的产品中所获得的收益.β(t11t12-p1)+(1-β)(t21t22-p2)做出最优采购量决策：

1)当β(t11t12-p1)+(1-β)(t21t22-p2)≥0时，采购方的总收益随着m的增加而增加，此时，最大化阶段1的最优采购量为M.

2)当β(t11t12-p1)+(1-β)(t21t22-p2)<0时，

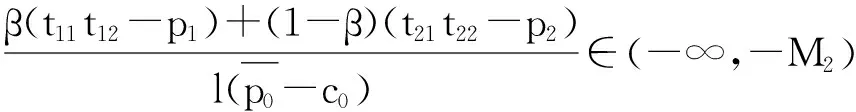
证明当采购方阶段1产品采购量分配比例为β时，其三个阶段的全部收益即为

π0=(β(t11t12-p1)+(1-β)×

(t21t22-p2))m+V0(m，β)

易知在β确定的情况下，V0(m，β)是关于m的增函数.所以，当β(t11t12-p1)+(1-β)(t21t22-p2)≥0时，π0是关于m的增函数.此时，采购方的总收益随着m的增加而增加，在能力范围内最大化m将是其最优策略，因此最优采购量为M.

当β(t11t12-p1)+(1-β)(t21t22-p2)<0时，决策m最大化π0就等价于最大化

m+q0(m)

⑨这里(t11t12-t21t22-p1+p2)的经济含义是阶段1中采购方(供应商 0)从供应商1与供应商2提供的单位产品中所获得的效用差.

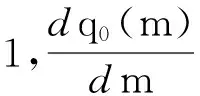
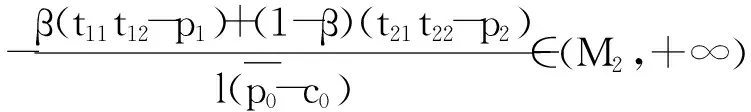
证毕.

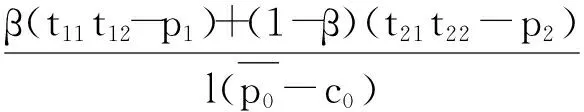
3.2最优分配比例决策

当采购量m确定，如何将其准确的分配给各个供应商(即确定分配比例β的值)，直接影响采购方在阶段1的收益以及阶段2的技术获取，并最终影响阶段3收益.此时采购方需要以利润最大化为目标，确定当阶段1产品采购量为m时的最优分配比例β.根据采购方的收益情况，可以给出定理4.

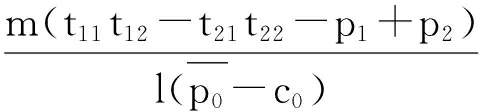
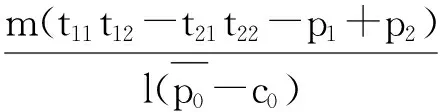
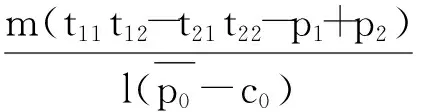
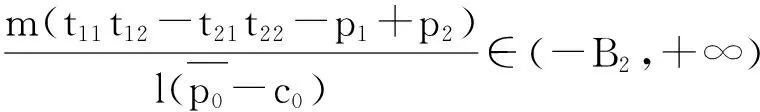
证明当采购方阶段1产品采购量为m时，其3个阶段的全部收益即为

π0=βm(t11t12-p1)+(1-β)m(t21t22-p2)+

V0(m，β)

β+q0)+m(t21t22-p2)

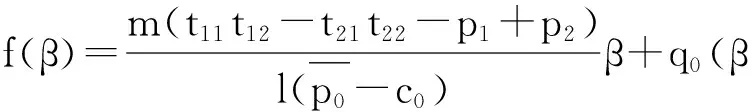
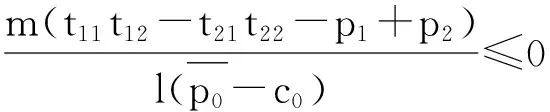
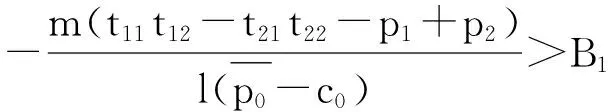
证毕.

3.3最优双变量组合决策

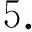
(5)

则该点即为采购方的最优决策点.其中

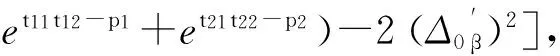
证明对于技术采购方，当不存在供应商技术研发时，在需要同时确定采购量m和分配比例β的情况下，其三个阶段全部收益为

(am)2t11t22(e-aβm+e-a(1-β)m)Δ0

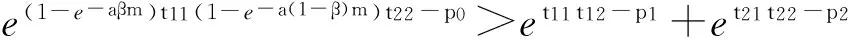
该点必为π0(m，β)在备选区域内的最大值点[18]，即为采购方的最优决策点.

证毕.

由定理5可以看出，企业在做采购量m和分配比例β的决策时，首先需要综合考虑当前期(购买时)和未来期(未来市场竞争)的总收益；其次需要考虑捆绑采购产品的技术水平组合，使得企业能从具有不同技术优势的供应商那获得相应的核心技术，经过组合吸收后能参与未来市场的竞争；最后还需要考虑当前期的采购价格、未来期净收益和总需求量对决策的影响.

综上所述，当中国政府和企业在做重大技术引进时，可以采取产品与技术捆绑采购的策略，在做具体决策时，不应只根据短期收益来制定采购策略，而应该根据当期产品的需求、自主吸收研发后在未来市场所面临的竞争等情况，来决策产品的采购量和不同供应商之间的分配情况，通过这种组合捆绑采购的方式，使企业既能获得最优的技术水平组合并且能够有实力参与未来市场的竞争.

4　算例分析

表2　阶段3市场可供选择的产品

4.1最优采购量决策

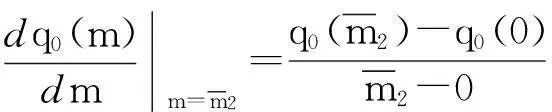
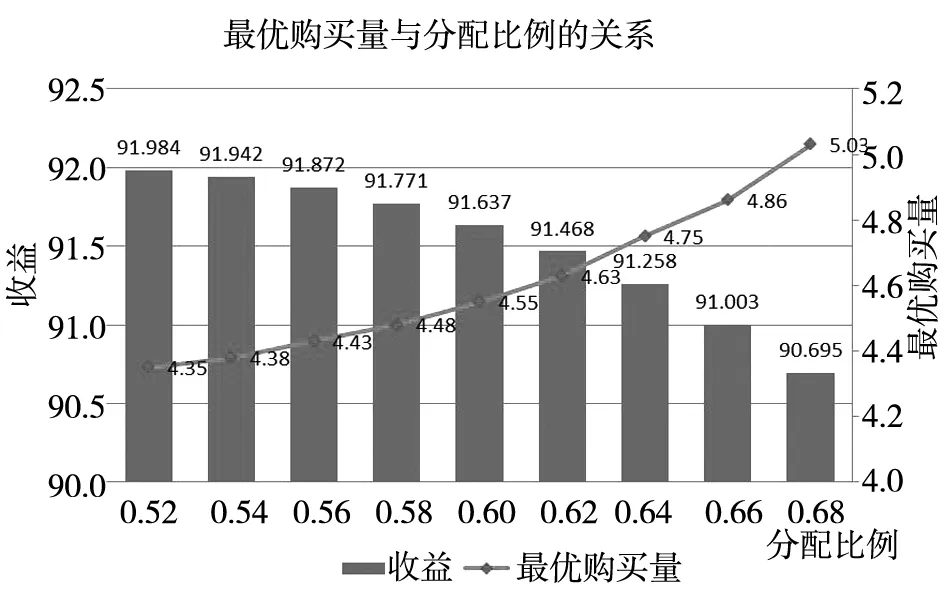
图3　分配比例变动时最优采购量/收益的变动

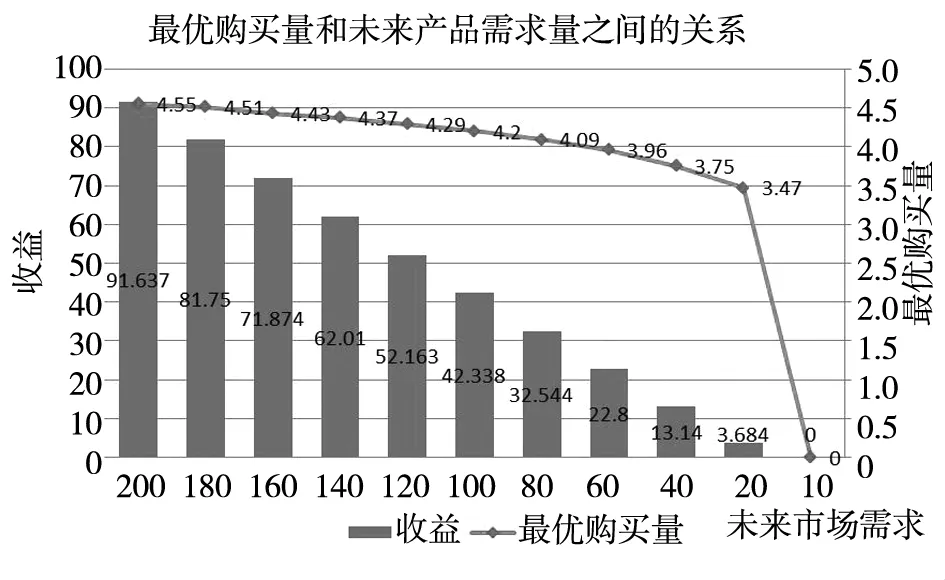
图4　未来市场需求变动时最优采购量/收益的变动

图5　供应商产品价格变动时最优采购量/收益的变动

图6　采购方单位产品成本变动时最优采购量和收益的变动

4.1.1分配比例β变动时最优采购量m*的变化

最优采购量的单变量决策是在分配比例β给定的情况下做出的，现在考虑β变动的情况下最优采购量m*的变化.从图3中可以发现，当分配比例增加时，最优采购量随之增加，而收益却相应减少.这主要是因为，在算例中给定的数据下，在阶段1中向供应商 1采购的产品比例越大，总体的单位产品收益将减少(供应商1的产品虽然技术水平较高，但同时价格也更贵，其产品效用比供应商 2的产品低).

4.1.2未来市场需求l变动时最优采购量m*的

变化

根据定理3，随着未来市场需求l的减小，最优采购量m*会不断减小，并在达到一定临界值时，由界内解跳跃为边界解.由图4可以看出当未来市场需求减少时，采购方的最优采购量也相应减少，并且当未来市场需求为10时，采购方的最优采购量发生跳跃，变为0.

4.1.3供应商技术捆绑产品价格p1变动时最优

采购量m*的变化

阶段1技术供应商的技术捆绑产品价格影响着采购方阶段1的产品收益，考察当阶段1供应商1的技术捆绑产品价格p1变动时最优采购量m*的变化.由图5可以看出，当阶段1供应商1的技术捆绑产品价格p1增大时，采购方阶段1的产品收益减少，进而导致总收益减少，采购方的最优采购量也相应减少.

4.1.4采购方单位产品成本c0变动时最优采购

量m*的变化

采购方单位产品成本c0影响采购方阶段3的销售收益，由图6可以看出，当采购方单位产品成本增加时，其最优采购量和总收益均呈下降趋势.

4.2最优分配比例决策

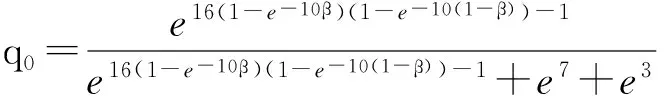
4.2.1采购量m变动时最优分配比例β*的变化

最优分配比例β*的单变量决策是在阶段1采购量m给定的情况下做出的，因此m的变动对其有着重要影响.图7可以看出，当阶段1产品采购量增加时，最优分配比例降低，同时总收益会先增加后减少.当产品采购量增加时，对采购方会产生两种影响：第一，采购量增加使得采购方所获得的技术水平增加，从而增大他在未来市场中的期望收益，进而增加总收益；第二，采购量增加会增加采购方的采购成本，进而减少总收益.根据图7可以看出，当采购量较小时，前者对于采购方的总收益影响更大，当采购量较大时，后者对于采购方的总收益影响更大.

4.2.2未来市场需求l变动时最优分配比例β*

的变化

未来市场需求l同样是影响最优分配比例的重要因素，从图8可以发现，当未来市场需求降低时，总收益降低，同时最优分配比例也降低.这是由于当未来市场需求降低时，阶段1的单位产品效用对于总收益的影响变得更大，因此采购方需要降低分配比例以增大阶段1的单位产品效用.

4.2.3技术捆绑产品价格p1变动时最优分配比

例β*的变化

4.2.4采购方产品单位成本c0变动时最优分配

比例β*的变化

图10表示阶段3采购方单位产品成本变化时，采购方最优分配比例和收益的变动.由图10可以发现，当采购方单位成本增加时，采购方的最优分配比例和收益均呈下降趋势，这是由于在给定的条件下，对于采购方，增加供应商2的产品采购量的边际收益比供应商1大，因此当成本增加时，最优分配比例相应下降.

图7产品采购量变动时最优分配比例/收益的变动

Fig. 7 The relationship of procurement quantity and the optimal allocation proportion (profit)

图8　未来产品需求量变动时最优分配比例/收益的变动

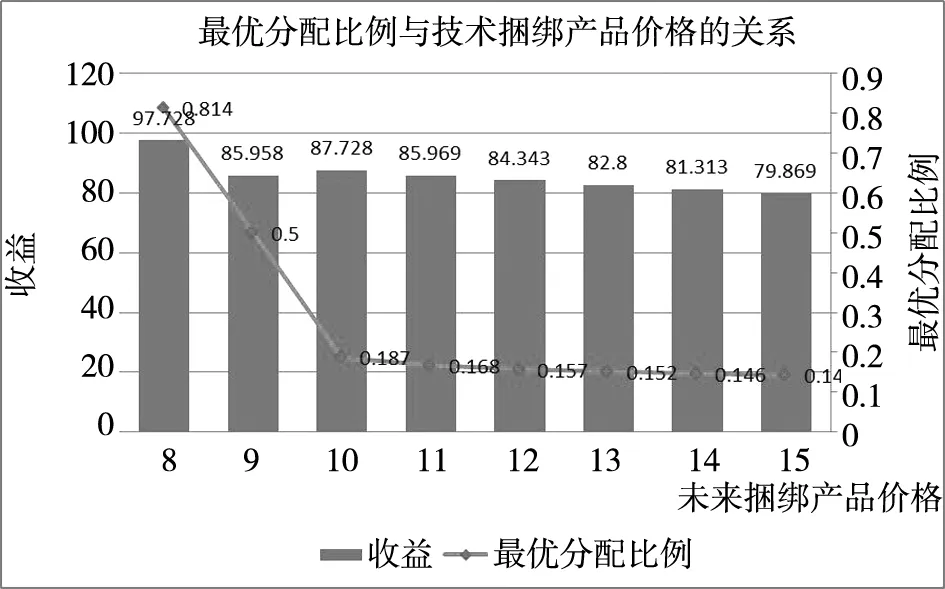
图9　供应商产品价格变动时采购方最优分配比例和收益的变动

图10　采购方产品单位成本变动时采购方最优分配比例和收益的变动

4.3最优采购量和最优分配比例双变量组合

决策

采购方3个阶段的全部收益即为

π0(m，β)=-2βm-(1-β)m+

根据定理5，求得满足最优解判定条件的双变量组合最优决策点为(m*，β*)=(4.51，0.433)，此时所获得的最大收益为π0(4.51，0.433)=92.587.

4.3.1未来市场需求l变动时最优采购量m*和

最优分配比例β*的变化

这里分析当未来市场需求发生变化时，最优采购量和最优分配比例双变量组合决策的变化.由图11可以发现*图11反映的是未来市场需求变化时双变量决策和总收益的变化，其中图像从左向右从上向下未来市场需求依次递减(空间坐标系中x、y、z轴分别代表分配比例、采购量和总收益).，当未来市场需求减少时，最优采购量m*和最优分配比例β*均减少.这是由于当未来市场需求减少时，阶段3采购方的市场份额也会相应减少，对于采购方来说阶段1的产品效用对于总收益影响更大，而阶段1此时的单位产品效用是小于0的，所以需要减少采购量，同时供应商1的产品效用比供应商2的产品效用小，相应的最优采购比例也会减小.

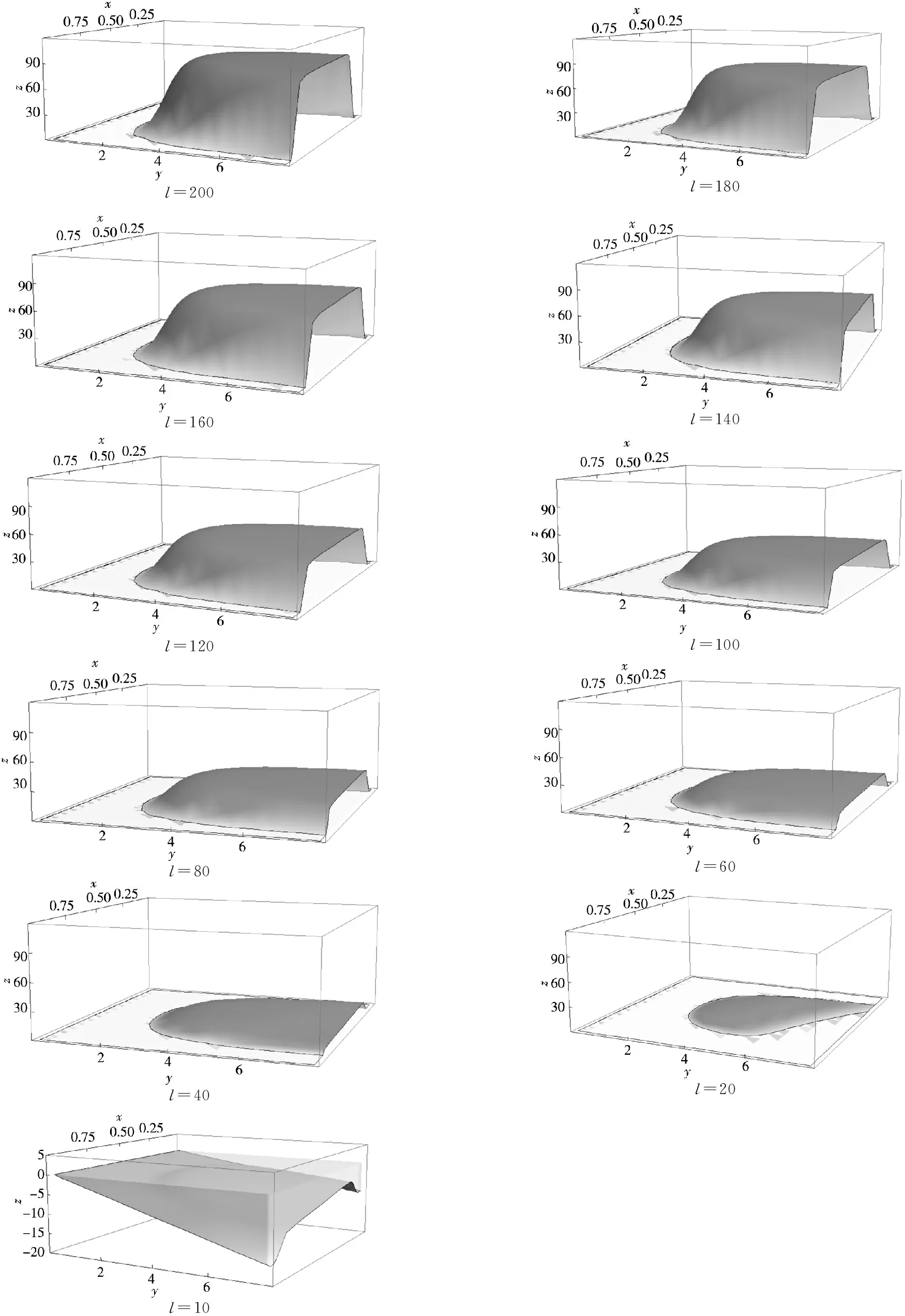
l=200l=180l=160l=140l=120l=100l=80l=60l=40l=20l=10

图11未来市场需求变化时双变量组合决策/总收益的变化

Fig. 11 The relationship of the future market demand and the bi-parameter decision problem (profit)

4.3.2捆绑产品价格p1变动时最优采购量m*和最优分配比例β*的变化

坐标系中x、y、z轴分别代表分配比例、采购量和总收益).

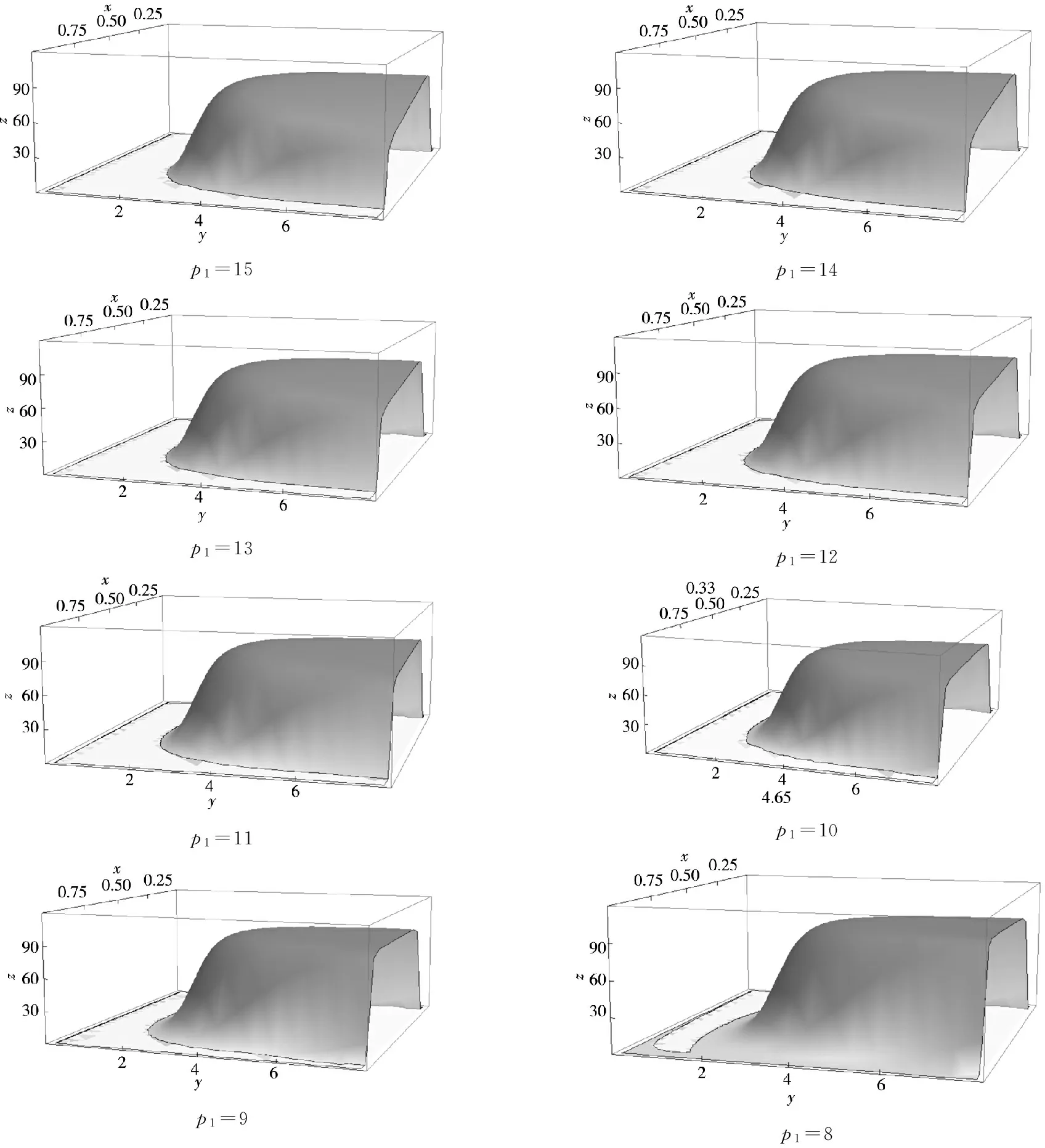
p1=15p1=14p1=13p1=12p1=11p1=10p1=9p1=8

图12供应商产品价格变化时双变量组合决策/总收益的变化

Fig.12 The relationship of price and the bi-parameter decision problem (profit)

4.3.3采购方产品单位成本c0变动时最优采购

量m*和最优分配比例β*的变化

c0依次递减(空间坐标系中x、y、z轴分别代表分配比例、采购量和总收益).

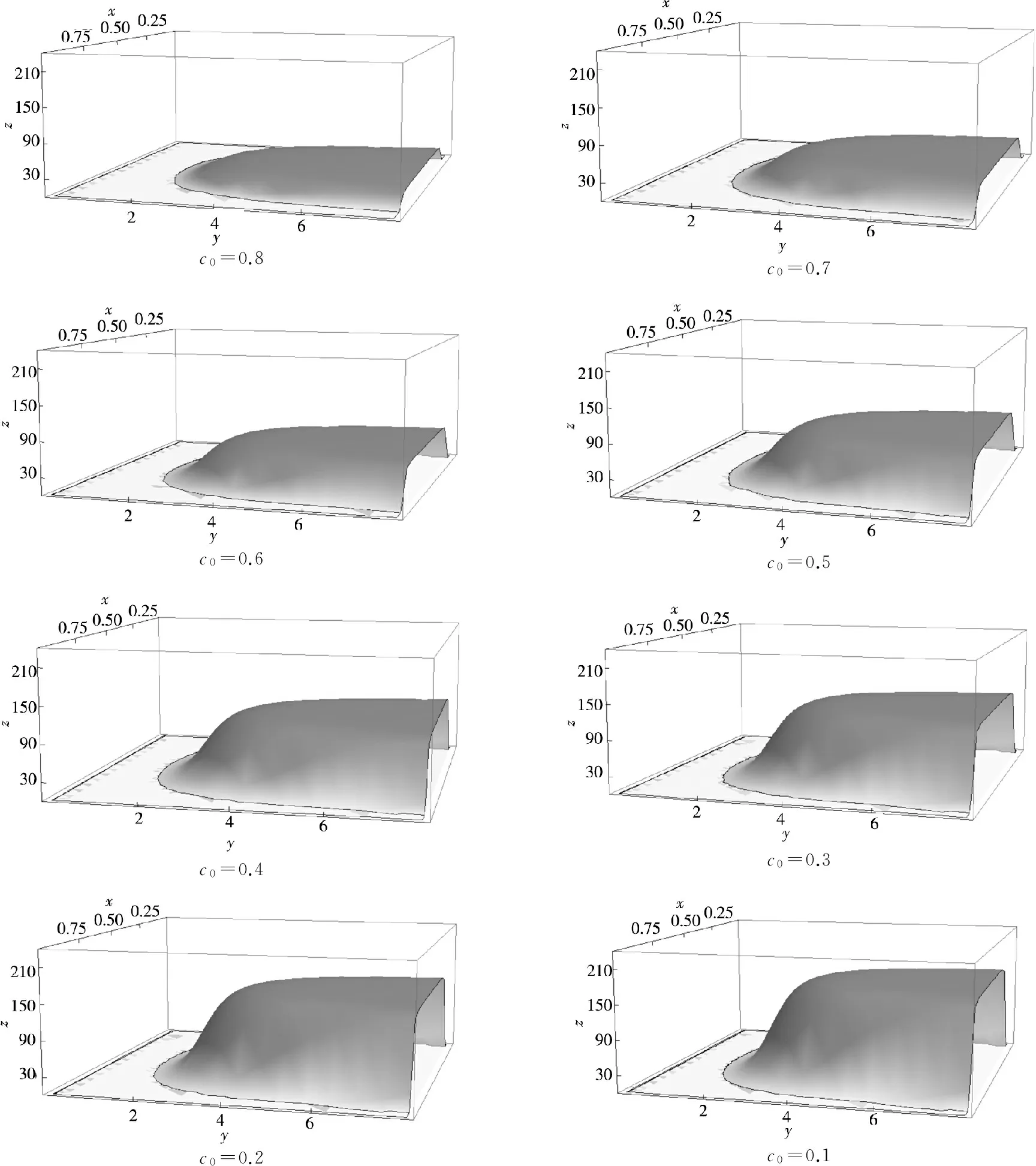
c0=0.8c0=0.7c0=0.6c0=0.5c0=0.4c0=0.3c0=0.2c0=0.1

图13采购方产品单位成本变化时双变量组合决策/总收益的变化

Fig.13 The relationship of unit product cost and the bi-parameter decision problem (profit)

5　结束语

随着经济的发展和产业的现代化升级，中国重大技术引进的方式和策略也成为学术界关注的焦点之一.由于飞机、火车、核电站等高新技术产品的技术门槛较高，只靠单个国家和企业的实力很难完成产品的自主研发及创新.因此，一些国家和企业通过“产品+技术”捆绑采购的形式进行技术引进.此时，采购方需要决策最优的采购量是多少？为了在未来市场的竞争中取得优势，采购方应如何通过在不同供应商之间分配采购比例来获得最优的技术转让水平？基于此，本文研究了具有技术转让的捆绑采购最优决策问题，用经典的消费者效用函数(柯布-道格拉斯函数)和离散选择模型(MNL模型)来研究技术捆绑采购过程中的最优采购量、最优分配比例问题，为未来国家进行重大技术引进提供一定的参考.通过研究得到以下结论：①有实力参与未来市场的竞争并在未来阶段获得较高利润是国家和企业在做重大技术设备采购量决策时需要考虑的关键因素.当采购量的分配比例确定时，即使在购买期采购单位产品的收益小于0，采购方还可以选择合适的采购量来获得最优的技术转让水平，进而通过未来阶段获得的收益来弥补购买期的损失.②当存在两家各具技术优势的供应商时，采购方应选择同时向两家企业捆绑采购产品和技术.当采购量确定时，若两家供应商实力相当且各具优势，采购方通过在不同供应商之间分配采购比例来获得两家供应商的优势技术水平，使得其参与未来期竞争的技术水平组合达到最优.③为了使购买期和未来期的总收益最大化，采购方需要同时做出最优采购量和最优分配比例的双变量决策.此时，采购方要考虑采购单位产品收益、供应商的技术优势和转让价格等因素对最优采购量和最优分配比例决策的影响.

当然，研究存在着一些局限和不足的地方，而这些也将为以后进一步的研究提供方向.①产品的价格决定.在模型设定中，技术产品在技术捆绑和非捆绑的情况下有两个确定的价格，与采购数量无关.然而，在现实市场中，产品价格有可能随着产品的采购量变化而变化.②供应商行为.在模型假定中，供应商只决定产品价格和技术转让，而不会有其他决策行为.而实际情况中，当供应商预测到的未来可能的竞争，可能会采取限制技术转让水平等行为，最终整个过程可能是双方共同博弈的结果，对于这些并没有考虑.

[1]Guiltinan J. The price bundling of services: A normative framework[J]. Journal of Marketing, 1987, (26): 74-85.

[2]Adams W, Yellen J. Commodity bundling and the burden of monopoly[J]. Quarterly Journal of Economics, 1976, (90): 475-498.

[3]Carbajo J, Meza D, Seidman D. A strategic motivation for commodity bundling[J]. The Journal of Industrial Economics, 1990, 38(3): 283-298.

[4]Chen Y. Equilibrium product bundling[J]. The Journal of Business, 1996, 70(1): 85-103.

[5]Matutes C, Regibeau P. Compatibility and bundling of complementary goods in a duopoly[J]. The Journal of Industrial Economics, 1992, 40(1): 37-54.

[6]Dansby R, Conrad C. Commodity bundling[J]. The American Economic Review, 1984, 74(2): 377-381.

[7]Bakos Y, Brynjolfsson E. Bundling information goods: Pricing, profits, and efficiency[J]. Management Science, 1999, 45(12): 1613-1630.

[8]彭赓, 寇纪淞, 李敏强. 信息商品捆绑销售与歧视定价分析[J]. 系统工程学报, 2001, 16(1): l-6.

Peng Geng, Kou Jisong, Li Minqiang. The analysis of information goods bundling selling and discrimination pricing[J]. Journal of Systems Engineering, 2001, 16(1): 1-6. ( in Chinese)

[9]吕魁, 胡汉辉, 王旭辉. 考虑范围经济与转换成本的混合捆绑竞争[J]. 管理科学学报, 2013, 16(12): l1-24.

Lü Kui, Hu Hanhui, Wang Xuhui. Bundling competition with scope economies and switching costs[J]. Journal of Management Sciences in China, 2013, 16(12): 11-24. (in Chinese)

[10]Hanson W, Martin K. Optimal bundle pricing[J]. Management Science, 1990, 36(2): 155-174.

[11]Mulhern F, Leone R. Implicitprice bundling of retail products: A multiproduct approach to maximizing store profitability[J]. Journal of Marketing, 1991, 55(4): 63-76.

[12]Johnson M, Herrmann A, Bauer H. The effects of price bundling on consumer evaluations of product offerings[J]. International Journal of Research in Marketing, 1999, 16(2): 129.

[13]Schmitz P. On monopolistic licensing strategies under asymmetric information[J]. Journal of Economic Theory, 2002, 106(1): 177-189.

[14]Yi S. Entry licensing and research joint ventures[J]. International Journal of Industrial Organization, 1999, 17(1): 1-24.

[15]Chu L, Wang Y. Bundled procurement for technology acquisition and future gain[J]. Manufacturing & Service Operations Management, 2015, 17(2): 249-261.

[16]田晓丽, 付红艳. 研发企业的技术传播途径选择研究[J]. 财经研究, 2013, 39(2): 70-80.

Tian Xiaoli, Fu Hongyan. Study on the choice of technology diffusion channels of R&D firms[J]. Journal of Finance and Economics, 2013, 39(2): 70-80. (in Chinese)

[17]McFadden D. Conditional Logit Analysis of Qualitative Choice Behavior in Frontiers in Econometrics[M]. New York: Academic Press, 1974: 105-142.

[18]陈朝晖. 二元函数凹凸性的判别法及最值探讨[J]. 高师理科学刊, 2010, 5: 25-28.

Chen Zhaohui. On the criterion of concave or convex and the most value of dual function[J]. Journal of Science of Teachers’ College and University, 2010, (5): 25-28. (in Chinese)

[19]春香. 德法日竞争中国高铁[J]. 交通与运输, 2006, (3): 26-27.

Chun Xiang. Germany, Japan and France bidding on China’s high-speed rail[J]. Transportation and Traffic, 2006, (3): 26-27. (in Chinese)

Optimal bundled procurement with technology acquisition

WEIHang,TANDan,LIPei

School of International Business Administration, Shanghai University of Finance and Economics, Shanghai 200433， China

In order to obtain advanced technology, technology buyers usually adopt the bundled procurement strategy which includes both product and technology. Technology buyers’ decisions on purchase quantity and allocation proportion in different suppliers will directly determine their total revenue when there are multiple technology suppliers on the market. Using a Cobb-Douglas function to express the utility in bundled procurement and a MNL model of technology bundle purchase to model the consumer behaviors, the paper studies the optimal decisions of purchase quantity and allocation proportion in different suppliers and the technology importer’s optimal decision in the process of technology introduction. With the MNL model, the optimal purchase quantity and allocation proportion can be determined to maximize technology buyers’ revenues. Furthermore, the bi-parameter decision problem is studied and the optimal conditions are given. At last, a numerical example is given to show the effectiveness of the model.

technology acquisition; bundling; MNL model; purchase quantity; allocation proportion

① 2014-05-31；

2016-01-06.

国家自然科学基金资助项目(71272016； 71571114).

魏航(1976—)， 男， 浙江绍兴人， 博士， 副教授. Email: weihang@mail.shufe.edu.cn

U116.2

A

1007-9807(2016)06-0001-19