一种减少供应链牛鞭效应的资产组合管理方法①

陈长彬， 盛　鑫， 梁永奕

(1. 清华大学现代物流研究中心， 北京 100083； 2. 电子科技大学中山学院， 中山 528402；3. 中山大学岭南学院， 广州 510275)



一种减少供应链牛鞭效应的资产组合管理方法①

陈长彬1, 2， 盛鑫3*， 梁永奕3

(1. 清华大学现代物流研究中心， 北京 100083； 2. 电子科技大学中山学院， 中山 528402；3. 中山大学岭南学院， 广州 510275)

考虑一个由单个供应商和多个零售商组成的供应链系统，零售商面临无促销活动和有促销活动两种动态需求环境，采用周期性检查库存策略，基于当前市场需求信息向供应商订货.同时，市场中的零售商由于订货决策行为的相互影响而存在一定的相关性.本文探讨零售商之间具有不同相关性订货决策时，运用资产组合管理方法调整零售商之间的供应量，减少订货的总方差，实现减少订货所产生牛鞭效应.随后，通过对比分析零售商订货量调整前后库存水平、库存成本、缺货损失和利润，验证了零售商调整订货量的动机和积极性.数值算例的结果表明，运用资产组合管理方法能够减少供应商的总方差，同时能够激励具有不同相关系数的零售商调整订货量，在一定程度上减少供应链中的牛鞭效应.零售商之间的相关系数越大，供应链中牛鞭效应减少的效果就越显著；且在同一相关系数下，零售商对市场需求预测的方差越大，运用资产组合管理方法所达到的牛鞭效应减少的效果就越大.

供应链； 依据水准订货策略； 牛鞭效应； 资产组合管理方法

0　引　言

牛鞭效应最早由宝洁公司的研究人员所发现，是指供应链中的需求变异放大现象，这种现象的存在及其对供应链的影响迅速引起了许多研究者的广泛关注，牛鞭效应主要是由于信息在供应链中传递过程的扭曲而产生的逐级放大效应，在定量模型中通常用方差变大来表示.从20世纪中期至今，许多学者为探讨牛鞭效应的存在及成因，做了大量深入的研究.Lee等提出了牛鞭效应概念的分析框架，根据该框架，牛鞭效应这个现象可从两个方面来证明，即行为层面和操作层面[1].行为层面主要是通过案例研究或实验室环境来验证，如系统动力学方法和啤酒游戏就是通过实验室的模拟仿真工具来进行实证分析；操作层面则包括16个主要的因素，即：需求预测，订货批量，价格波动，理性与短缺博弈[2]，提前期[3]，库存策略[4]，补货策略[5]，不当的控制系统，乘数效应[6]，缺乏透明度[7,8]，节点数，生产能力限制[9,10]，缺乏同步[11]，回馈误觉，没有全局视野的局部优化，公司流程[12].

达庆利等在前人研究的基础上，总结了减轻和削弱牛鞭效应的多种对策[13]，如信息共享[1]、VMI[14]、采购承诺和数量柔性等其他方法.Chen等也证明了通过把需求信息集中化可以部分减少牛鞭效应[15]，万杰等也从生产商和零售商利用各自库存策略处理信息的结果得到类似的结论[16].近年来，关于牛鞭效应的研究也引入了控制论等新方法，部分学者通过运用控制论以及H∞鲁棒控制方法探讨削减牛鞭效应的具体途径[17-21].有学者则从反牛鞭效应的角度来研究如何减少牛鞭效应，如李刚等最早提出并验证了供应链中反牛鞭效应的存在，为削弱牛鞭效应开辟了一个新途径[22].庄伟卿等也进一步从博弈论的角度论证了反牛鞭效应在减少牛鞭效应中的作用[23].此外，从预测方法的角度，主要探讨各种预测技术对牛鞭效应的影响[24,28].

在以往关于牛鞭效应研究中，大部分假设包含单个供应商和单个零售商所组成的两级供应链，但实际上，在许多供应链中，供应商通常面对多个零售商的订货需求，而零售商在进行订货决策时往往都要考虑彼此的决策行为，在同一市场中零售商的订货决策行为之间存在着一定的相关性.因此，可以考虑存在多个理性的零售商向供应商订货决策时，零售商在确定市场需求时需要同时考虑彼此订货量的相互影响.零售商之间订货量的调整可能在一定程度上减少向供应商订货的总方差，从而有利于削弱牛鞭效应，这是本文研究的主要目的.本文将探讨存在单个供应商和多个零售商的两级供应链中，当零售商之间具有不同相关性的情况下向供应商订货的决策，并运用资产组合管理方法来减少零售商向供应商订货时所产生的牛鞭效应，这也是本文与其他研究的区别所在.

1　基本模型构建

1.1零售商无促销活动下的模型构建

在动态需求环境下，考虑一个由单个供应商和多个零售商组成的供应链系统，零售商采用周期性检测库存策略，基于当前市场需求信息向供应商订货.假设零售商没有采取促销行为，根据Kahn提出的市场需求预测模型，其基本思想认为未来的需求必然与当前的需求存在着某种关系[29]，这种关系可以表示为如下模型

Di,t=di+ρDi,t-1+εi,t，

i=1,2,…,n

(1)

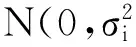
(2)

(3)

由Heyman和Sobel的研究结果可知[30]，对具有如式(1)所表示的需求特征的产品来说，当第i个零售商在时期t末决定订货量为Qi,t时，为了达到从订货到需求发生这段时期内的库存与缺货成本的期望值最小，即使从订货到需求发生这段时间内的利润达到最大，应采取order-up-to(依据水准订货)的订货策略来确定该时期零售商的订货水平Si,t.当零售商获知第t期的市场需求量Di,t后，应确定Si,t，并根据如下公式来确定订货量Qi,t,即

Qi,t=Di,t+(Si,t-Si,t-1)

(4)

其中

(5)

且

(6)

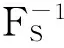
由Heyman和Sobel的推导结果可知，零售商订货的最优订货依据水准应为

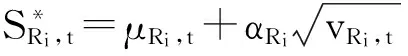
i=1,2,3,…,n

(7)

其中μRi,t和vRi,t分别表示基于第t期的市场需求量Di,t的均值和方差，则

(8)

(10)

进一步地，将式(1)代入式(10)，可得

且

(11)

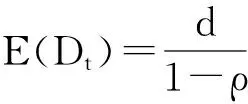
由式(11)，零售商可以根据分析和预测的市场需求量依次决定各个期间所决定的订货数量.

1.2零售商有促销活动下的模型构建

根据Raghunathan的研究结果，当零售商在前一期有促销行为时，该市场需求特征可表示为

DPi,t=di+ρDi,t-1+qXi,t-1+εi,t-1

i=1,2,…,n

(12)

i=1,2,3, …,n

(13)

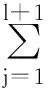
(14)

(15)

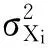
(16)

与式(1)需求分布特征类似，由零售商订货量Qi,t与需求量DPi,t之间的关系表达式可得

(17)

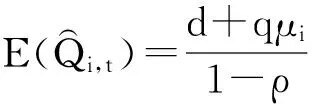
1.3零售商订货量方差分析

零售商无论是否有促销行为，根据order-up-to level 策略进行订货量的决策，订货数量与实际的市场需求均会产生一定的方差，具体方差的产生取决于多个方面的因素，为简化分析，不妨以无促销活动下的市场需求特征为例来分析，根据式(1)、式(3)和式(4)，零售商订货量的方差可表示为

i=1,2,…,n

(18)

从方程(5)可以看出，当零售商采用最优库存策略时，也就是零售商进行所谓“理性决策”将会造成信息的扭曲，即产生“牛鞭效应”.供应链末端需求的方差将会通过提前期、订货周期、零售商之间订货的相关系数以及各个预测的参数等多个变量不断放大.

从式(10)可以得出所有零售商向供应商的总订货量为

(19)

方差为

(20)

方程(20)说明了零售商总订货量的方差取决于零售商需求量的相关性而不是每个零售商订货量之间的相关性.当相关系数rij为正值时，零售商总订货量的方差将增加，反之，零售商总订货量的方差将下降.实际上，当市场需求处于高增长时期，rij一般取正值，但市场需求处于较平稳的时期，rij一般取负值，原因在于较为成熟的市场增长不快，零售商要提高自己销售额，就必然从其他的零售商吸引顾客，从而构成了零和博弈.因而，不同零售商的订货量必然有升有降，这主要取决于零售商的促销行为，但对供应商来说总订货量可能是不变的.根据以上分析，又因为

所以，可得

(21)

在市场需求是随机的情况下，零售商总订货量的方差将会减小.Zinn等认为，对于供应商来说，必须把所有零售商的需求量加总来估计总订货量方差[31].该理论的根据是所有零售商都是采用同一种市场促销策略，但这与实际并不相符，所以，基于所有零售商总需求量数据进行的市场预测比基于单个零售商需求量数据进行预测的结果还更不准确.

2　减少牛鞭效应的资产组合管理方法

2.1牛鞭效应的衡量及资产组合管理方法的运用

根据Simchi-Levi等人的研究结果[32]，可以用式(22)衡量牛鞭效应的大小.

(22)

从式(18)可以看出，当BE≤0时，供应商需求量的方差将会减小.进一步地，将式(18)和式(20)代入式(22)，可得

(23)

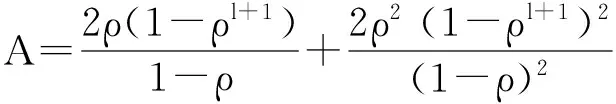
由于ρ>0,对于任何两个零售商之间的相关系数均为负值，即对于所有零售商，当i≠j时，所有的rij=-1,从式(23)可以看出，供应商的需求量方差存在着一个最小值.

由以上分析可知，对于供应商来说，通过零售商彼此之间的信息共享可以在一定程度上减少牛鞭效应.但是，供应商对于那些来自零售商的促销行为等因素所产生的需求量方差却无法采取有效的措施，这将导致严重的牛鞭效应.因而，为有效减少供应链中的牛鞭效应，可以考虑在保持市场中所有零售商订货总量不变的条件下，对每个零售量的订货数量进行调整，本文运用资产投资组合方法确定每个零售商在订货时应增加或减少的订货数量，从而通过对零售商订货数量的重新分配达到减少牛鞭效应的目的.其原理在于根据资产投资组合理论，投资者应该进行多元化组合投资，可以产生最大的预期收益和最小的方差，借鉴该理论，要最大程度地减少供应链中的牛鞭效应可以通过最小化零售商的订货方差来实现，具体如下：

令Xi为第i个零售商的一个正的调节系数，在第t期，市场中实际的供应数量可以表示为XiQi,t,目标的库存量水平为XiSi,t.根据资产组合管理理论，可以通过设定一系列调节系数Xi,i=1,2,…,n,使总订货量的方差达到最小.基本模型如下式所示

minVar(QR,t)=Var(X1Q1,t+

X2Q2,t+…+XnQn,t)

(24)

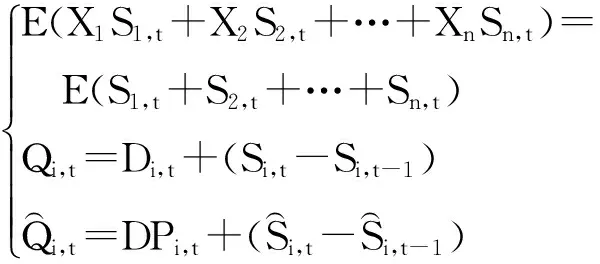
Xi>0,i=1,2,…,n

由于Xi>0,则

由于质心是物质系统上被认为质量集中于此的一个假想点，表示质量分布的平均位置，故可以据此来确定撒料点在撒料区域中的平均位置，以确保最终撒料能够覆盖到实际需要撒料区域.设撒料区域像素点集合 Ui中的元素是 p（x，y），n 为集合 Ui内像素点总数量，质心坐标 Z（x，y）的求解公式为式（9）.

(25)

否则，当Xi<0时，则

(26)

从式(26)可知，所有其他的供货数量将为负数或0，而这显然是不可能的.

由于两种需求特征不同的市场订货量分别可表示为

Qi,t=Di,t+(Si,t-Si,t-1)=ρl+1Di,t+

假设存在单个供应商与R1和R2两个零售商，正常情况下R1的销售量更大，但R2在t-1期单方采取促销行为来提高需求量的情况下，如何预测本期双方的市场需求量和和决定订货量以及减小由此而产生的牛鞭效应就成了本文要研究的主要问题.

2.2在零售商R2促销条件下双方需求量相等时

根据以上假设，当R2在前一期通过促销手段使得两个零售商的市场平均需求量相等，即：令di=E(Qi,t)=d,i=1,2.因而，两个零售商的期望订货量是相等的.在零售商双方独立决策的情况下，R2会根据式(12)的市场需求特征模型决定订货量.在两种不同需求特征情况下，有促销活动的R2订货量的方差会高于无促销活动的R1，即Var(Q2,t)>Var(Q1,t)，因而，从式(20)可得

minVar(QR,t)=Var(X1Q1,t+X2Q2,t)

(27)

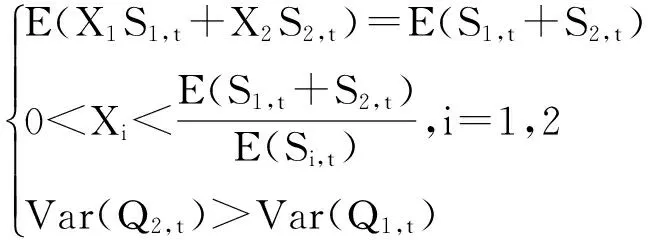
由于假设每个零售商的平均订货数量都是相等的，即

(28)

把式(28)代入式(27)，可得

minVar(QR,t)=Var(X1Q1,t+X2Q2,t)

(29)

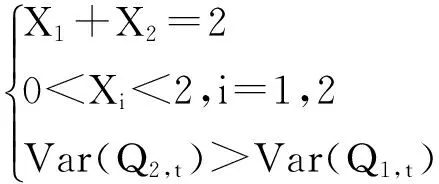
相应地，可知总订货量QR,t的方差为

2X1(2-X1)Cov(Q1,t,Q2,t)

(30)

由式(29)、式(30)，可得

(31)

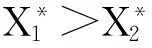
2.3在零售商R2促销条件下需求量不同的模型

在式(38)中是假定R2在通过促销行为销售量得到提高，因而使得原来R2在需求量小于R1的情况下实现双方的市场平均需求量相同，从而所有零售商向供应商订货的数量是相同的.但实际上，每个零售商的订货数量通常取决于顾客的需求量大小，如果R1需求量远大于R2，R2即使通过促销手段获得一定的销售量增加，在短期内也难以在市场中获得与R1平起平坐的地位.因而，R2可能从R1夺取一部分的市场需求量，但总体上，R2的需求量还是要比R1小.当两个零售商的订货量不同的情况下，对供应商供货数量也相应地产生影响.

假设d1≠d2，di=E(Si,t)，由于E(X1S1,t+X2S2,t)=E(S1,t+S2,t)，可以推出X1d1+X2d2=d1+d2，所以，式(24)可重新表示为

minVar(QR,t)=Var(X1Q1,t+X2Q2,t)

(33)

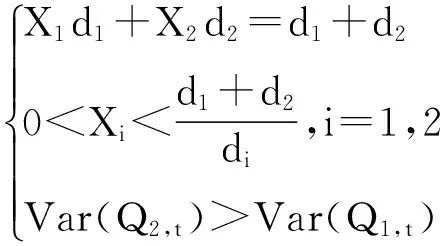
由式(33)可解得

(34)

(35)

从式(34)、式(35)可以看出，对于零售商订货量的分配比率取决于期望订货量和订货方差.不失一般性，为简化分析，本文以零售商之间的订货需求量相等时为例来讨论.

(36)

从式(36)可以看出，当市场上最终消费者的需求彼此高度正相关时，即当r12→1时，式(34)和式(35)中无法找到一个可行解来减少总需求的方差.

2.4采用资产组合管理方法前后零售商的分析

与比较

2.4.1调整订货量前后零售商平均总库存水平

与单个零售商库存水平的分析与比较

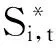
(37)

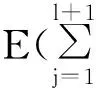
(38)

(39)

由于订货量调整前零售商R1和零售商R2的平均库存水平分别为

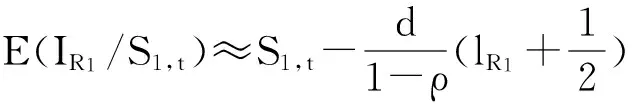
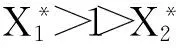
2.4.2调整订货量前后零售商库存机会成本的

分析与比较

R1在未调整订货量前的库存成本与短缺损失的表达式为

(40)

E(CR1(Q1,t))=[2(p-cR1)+hR1]×

(41)

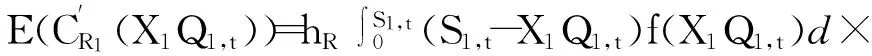
S1,t)f(X1Q1,t)d(X1Q1,t)

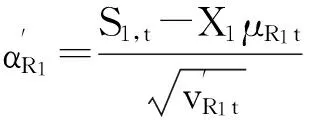
(42)

E(CR1(Q1,t))=[2(p-cR1)+hR1]×

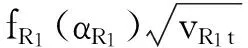
(43)

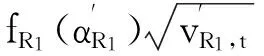
(44)

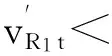
E(CR2(Q2,t))=[2(p-cR2)+hR2]×

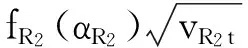
(45)

且

(46)

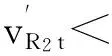
从以上对R1和R2在调整订货量前后的库存成本与短缺损失来看，通过赋予某个调整因子调整订货量后，R1和R2的库存成本与短缺损失均减小了.2.4.3调整订货量前后零售商利润的分析与比较

Q1,t)]f(Q1,t)dQ1,t

(47)

则R1在未调整订货量前的期望利润可表示为

[2(p-cR)+hR][αR1FR(αR1)+

(48)R1在调整订货量后的期望利润可表示为

(49)

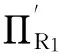
2.4.4供应商的需求方差

零售商在调整订货量前的供应商需求量方差可以表示为

Var(QR,t)=Var(Q1,t)+Var(Q2,t)+

2Cov(Q1,t,Q2,t)

而在零售商调整订货量后，供应商需求量的方差可表示为

Cov(Q1,t,Q2,t)+4Var(Q2,t))

(50)

把式(31)代入式(50)，得

(51)

因此，对于供应商的需求量方差的减少数值大小为

由上式，可以进一步求得供应商需求量减少的方差的比率为

(52)

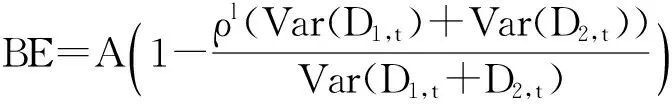
BE*=

则由式(31)、式(32)可得

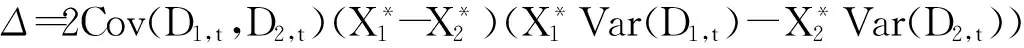
3　算例分析

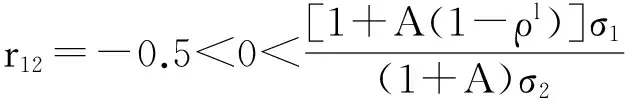
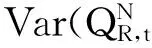
(53)

2)R1与R2之间有信息共享的情况下，两个零售商分别就订货量进行决策存在一定的相关性，零售商向供应商订货的总需求量方差用Var(QR,t)表示，可得

Var(QR,t)=Var(Q1,t)+Var(Q2,t)+

2Cov(Q1,t,Q2,t)=

(54)

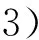
(55)

进一步地，可以把r12的取值推广至一般的情况，分别取各个不同的相关系数，同时其余的参数分别仍旧取原来的值，即r12=-0.1～-0.9时，k分别取1.2，1.4，1.6，1.8以及2.0，如表1所示.同样地，当r12=0.1～0.9时，k分别取1.2，1.4，1.6，1.8以及2.0，如表2所示.另外，根据前文的分析

(56)

1)当r12<0时

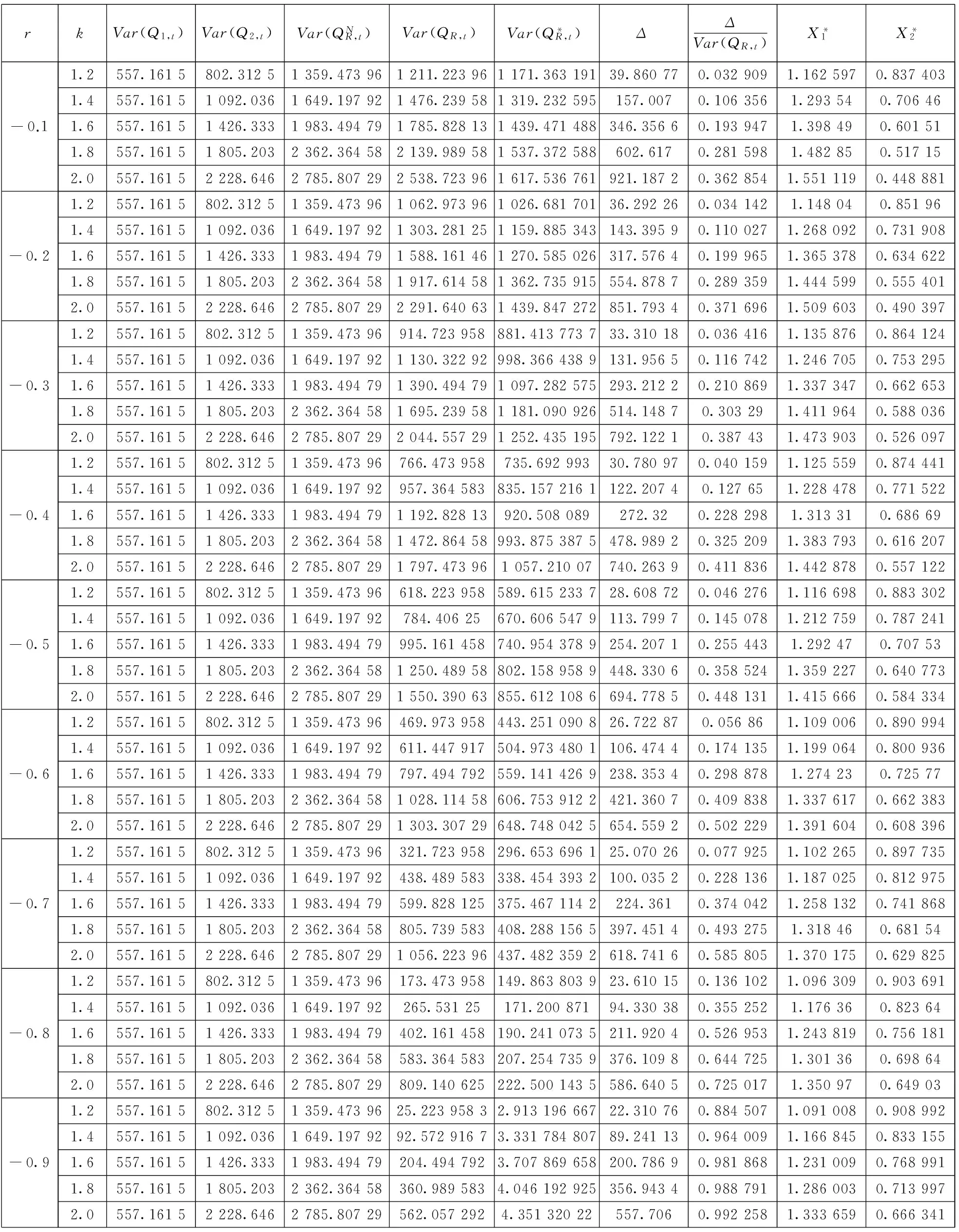
表1　数值模拟中的参数设定(r12<0)

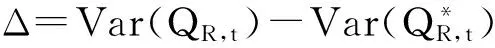
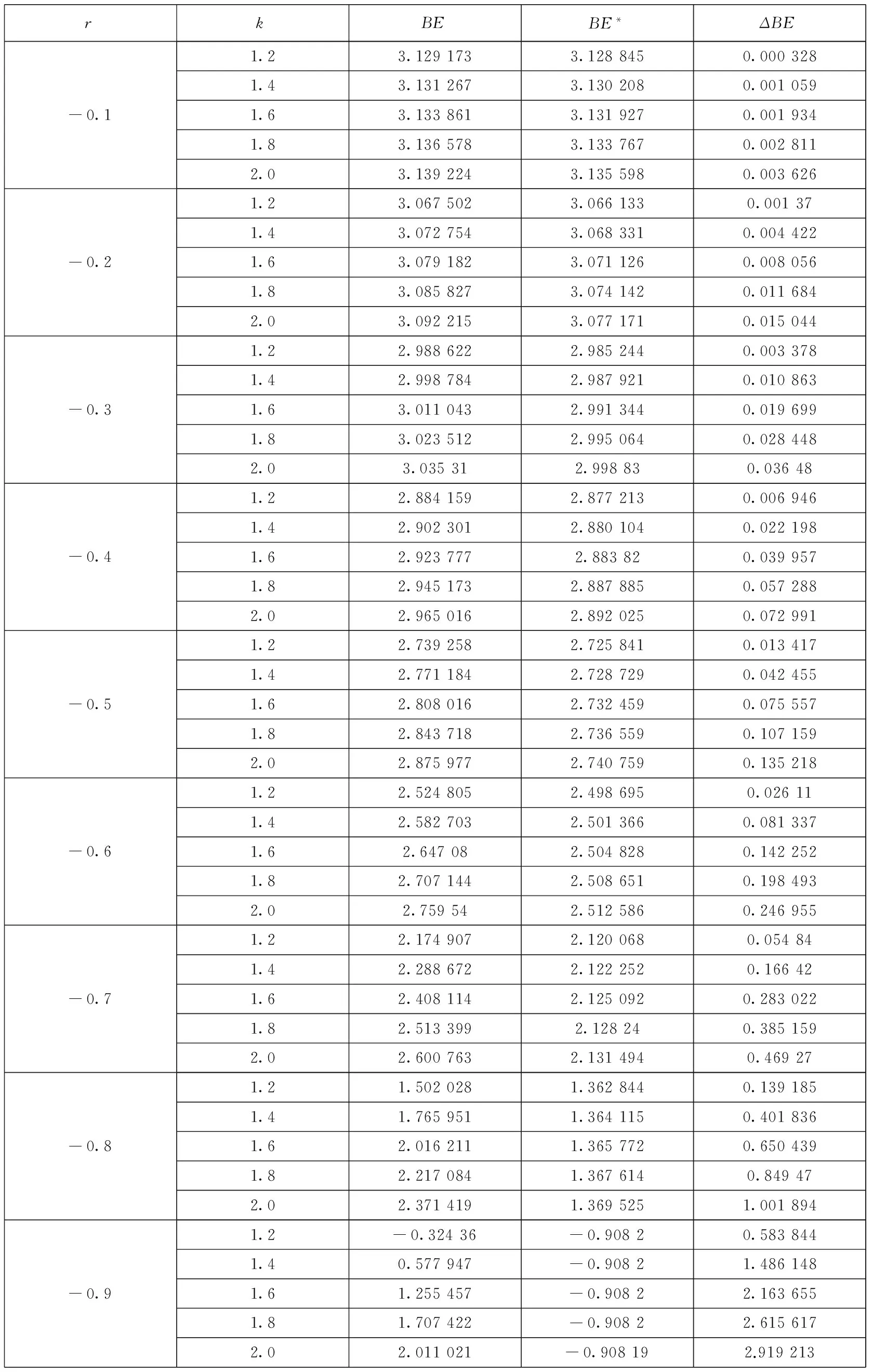
表2　不同参数(r12<0)时的牛鞭效应

2)当r12>0时

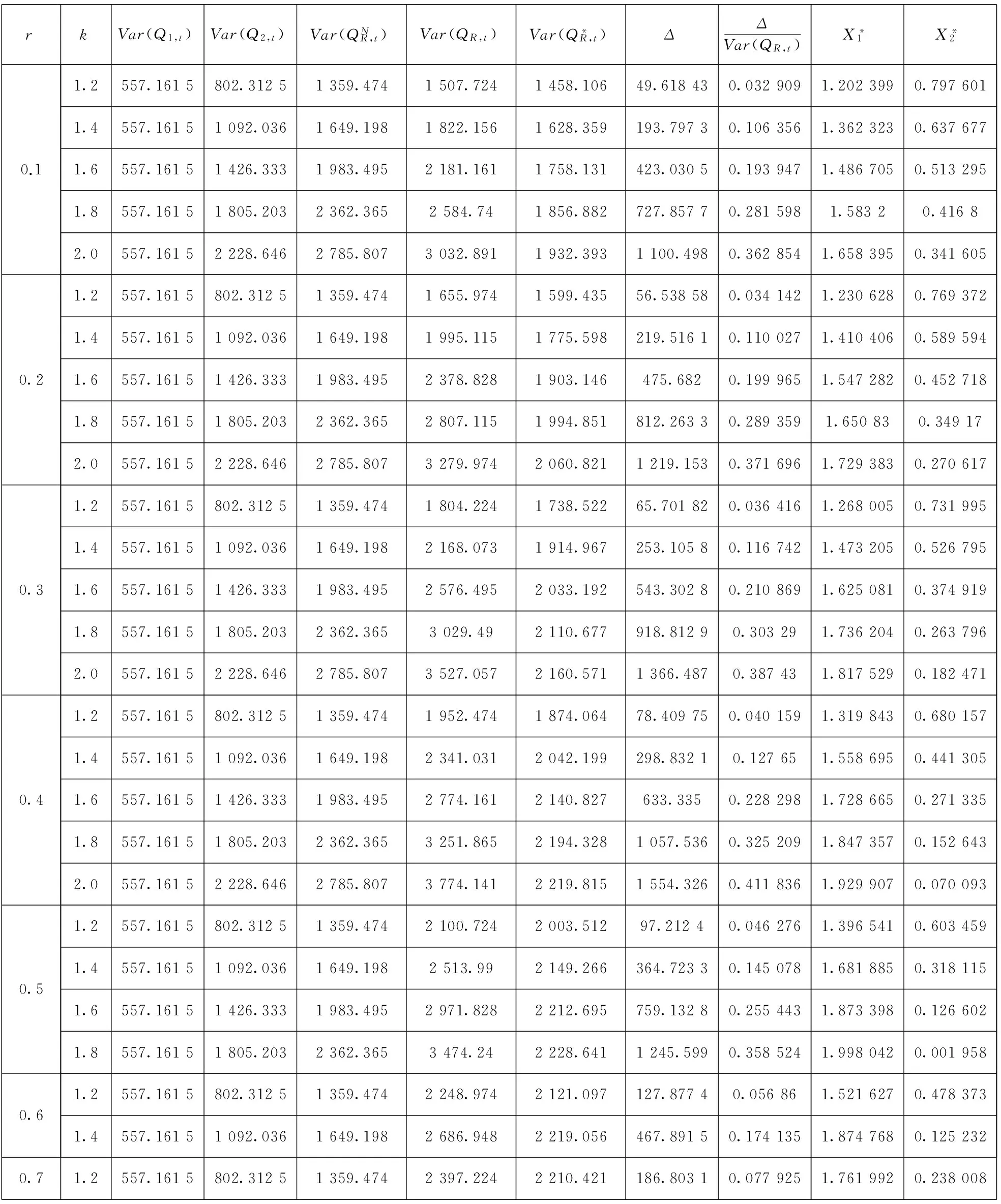
表3　数值模拟中的参数设定(r12>0)

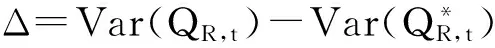
表4　不同参数(r12>0)时的牛鞭效应

从表1、表2的数值计算结果可知，当r12≠0时，不管k的取值是多少，通过资产组合管理方法所确定的调节系数X1和X2，均使得BE*

4　结束语

供应链中由于牛鞭效应的存在使得上下游企业往往不能获取准确的需求和供应信息，这将极大地影响供应链的整体绩效，从而无法达到最优水平，因而，不论对于整条供应链，还是供应链中的节点企业，采取有效的措施或设计优化的策略来对其进行协调从而减少牛鞭效应都是十分必要的.供应链中的上下游企业如果信息无法实现共享，那对双方来说，要么可能导致更高的安全库存，从而要负担更高的库存成本，要么可能会产生大量的缺货成本.以往关于供应链信息共享或牛鞭效应的研究主要基于上下游企业双方对市场需求的预测，在本文中，尝试采用资产组合管理方法并结合市场需求的预测信息来减少供应链中的牛鞭效应，同时在此基础上可以改善供应链的整体绩效.

从本研究的分析结果可以看出，通过运用资产组合管理方法可以减少供应商的总方差，对于零售商不论相关系数大于零或小于零，即不管零售商彼此的需求是正相关还是负相关，都能够在一定程度上减少供应链中的牛鞭效应，且相关系数的绝对值越大，减少牛鞭效应的效果就越好，而且在同一相关系数下，零售商对市场需求预测的方差越大，运用资产组合管理方法所减少的牛鞭效应的效果就越大.

[1]Lee H L, Padmanabhan V, Whang S. The bullwhip effect in supply chains[J]. Sloan Management Rev., 1997, 38(3): 93-102.

[2]Lee H L, Padmanabhan V, Whang S. Comments on information distortion in a supply chain: The bullwhip effect[J]. Management Science, 2004, 50: 1887-1893.

[3]Heydan J, Kazemzadeh R B, Chaharsooghi S K. A study of lead time variation impact on supply chain performance[J]. International Journal of Advanced Manufacturing Technology, 2009, 40: 1206-1215.

[4]Aharon B T, Boaz G, Shimrit S. Robust multi-echelon multi-period inventory control[J]. European Journal of Operational Research, 2009, 199: 922-935.

[5]Su C T, Wong J T. Design of a replenishment system for a stochastic dynamic production/forecast lot-sizing problem under bullwhip effect[J]. Expert System with Application, 2008, 34: 173-180.

[6]Geary S, Disney S M, Towill D R. On bullwhip in supply chains-historical review, present practice and expected future impact[J]. Int. J. Production Economics, 2006, 101: 2-18.

[7]Sohn S Y, Lim M. The effect of forecasting and information sharing in SCM for multi-generation products[J]. European Journal of Operational Research, 2008, 186: 276-287.

[8]Agrawal S, Sengupta R N, Shanker K. Impact of information sharing and lead time on bullwhip effect and on-hand inventory[J]. European Journal of Operational Research, 2009, 192: 576-593.

[9]Alony I, Munoz A. The bullwhip effect in complex supply chains[C]. International Symposium on Communications and Information Technologies on IEEE, 2007, 1355-1360.

[10]Nepal B, Murat A, Chinnam R B. The bullwhip effect in capacitated supply chains with consideration for product life-cycle aspects[J]. Int. J. Production Economics, 2012, 136: 318-331.

[11]Erkan B, Lenny Koh S C, Gunasekarn A, et al. The role of forecasting on bullwhip effect for E-SCM applications[J]. Int. J. Production Economics, 2008, 113: 193-204.

[12]Moyaux T, Chaib-draa B, D’Amours S. Information sharing as a coordination mechanism for reducing the bullwhip effect in a supply chain[J]. IEEE Transaction on Systems, Man and Cybernetics Part C: Applications and Reviews, 2007, 37: 396-409.

[13]达庆利， 张钦， 沈厚才. 供应链中牛鞭效应问题研究[J]. 管理科学学报， 2003, 6(3)： 86-93.

Da Qingli, Zhang Qin, Shen Houcai. Study on bullwhip effect in supply chain[J]. Journal of Management Sciences in China, 2003, 6(3)： 86-93.(in Chinese)

[14]Disney S M, Towill D R. The effect of vendor managed inventory (VMI) dynamics on the bullwhip effect in supply chains[J]. Int. J. Production Economics, 2003, 85: 199-215.

[15]Chen F, Drezner Z, Ryan J K, et al. Quantifying the bullwhip effect in a simple supply chain: The impact of forecasting, lead time, and information[J]. Manage Sci., 2000, 46(3): 436-443.

[16]万杰， 寇纪松， 李敏强. 需求信息预测与处理中的牛鞭效应[J]. 天津大学学报， 2003, 36(3)： 369-373.

Wan Jie, Kou Jisong, Li Minqiang. Bullwhip effect in demand forecasting and processing[J]. Journal of Tianjin University, 2003, 36(3)： 369-373. (in Chinese)

[17]Dejonckheere J, Disney S M, Lambrecht M R, et al. Measuring and avoiding the bullwhip effect: A control theoretic approach[J]. European Journal of Operational Research, 2003, 147: 567-590.

[18]黄小原， 郭海峰， 卢震. 供应链时滞系统模型及其牛鞭效应的H∞控制[J]. 系统工程学报， 2005, 20(6)： 585-590.

Huang Xiaoyuan, Guo Haifeng, Lu Zhen. H∞control of supply chain time delay system model and its bullwhip effect[J]. Journal of Systems Engineering, 2005, 20(6)： 585-590. (in Chinese)

[19]罗卫， 张子刚， 欧阳明德. 基于DE-APIOBPCS策略的牛鞭效应和库存方差[J]. 中国管理科学， 2005, 13(2)： 88-94.

Luo Wei, Zhang Zigang, Ouyang Mingde. Bullwhip effect and inventory variance based DE-APIOBPCS policy[J]. Chinese Journal of Management Science, 2005, 13(2)： 88-94. (in Chinese)

[20]唐亮， 靖可. H∞鲁棒控制下动态供应链系统牛鞭效应优化[J]. 系统工程理论与实践， 2012, 32(1)： 155-163.

Tang Liang, Jing Ke. Bullwhip effect optimization of dynamic supply chain system based on H∞robust control[J]. Systems Engineering: Theory & Practice, 2012, 32(1)： 155-163. (in Chinese)

[21]魏永长， 王红卫， 祁超, 等. 横向调货策略下供应网络中牛鞭效应的鲁棒控制[J]. 系统工程学报， 2013, 28(5)： 633-640.

Wei Yongchang, Wang Hongwei, Qi Chao, et al. Robust control for the bullwhip effect of a supply network under the lateral transshipment policy[J]. Journal of Systems Engineering, 2013, 28(5)： 633-640.(in Chinese)

[22]李刚， 汪寿阳， 于刚, 等. 牛鞭效应与生产平滑模型有效性问题[J]. 管理科学学报， 2004, 7(1)： 1-18.

Li Gang, Wang Shouyang, Yu Gang, et al. Bullwhip effect and validity of production-smoothing model[J]. Journal of Management Sciences in China, 2004, 7(1)： 1-18.(in Chinese)

[23]庄伟卿， 刘震宇. 牛鞭效应弱化与反牛鞭效应强化在完美信息下联合作用的博弈[J]. 数学的实践与认识， 2012, 42(13)： 20-31.

Zhuang Weiqing, Liu Zhenyu. Game of the combined effects of bullwhip effect weaken and anti-bullwhip effects strengthen under the perfect information[J]. Mathematics in Practice and Theory, 2012, 42(13)： 20-31. (in Chinese)

[24]Wright D, Xin Yuan. Mitigating the bullwhip effect by ordering policies and forecasting methods[J]. Int. J. Production Economics, 2008, 113: 587-597.

[25]章魏， 华中生. 多产品供应链的牛鞭效应及其减弱方法[J]. 系统工程学报， 2010, 25(4)： 479-483.

Zhang Wei, Hua Zhongsheng. Bullwhip effect in multi-product supply chain and its weakened method[J]. Journal of Systems Engineering, 2010, 25(4)： 479-483.(in Chinese)

[26]马云高， 王能民， 徐金鹏. 供应链零售商预测技术研究——基于牛鞭效应的视角[J]. 运筹与管理， 2013, 22(3)： 53-60.

Ma Yungao, Wang Nengmin, Xu Jinpeng. Analysis of retailer’s forecasting techniques in supply chain: Based on the bullwhip effect[J]. Operations Research and Management Science, 2013, 22(3)： 53-60. (in Chinese)

[27]Li Qinyun, Stephen M Disney, Gerard Gaalman. Avoiding the bullwhip effect using damped trend forecasting and the Order-Up-To replenishment policy[J]. Int. J. Production Economics, 2014, 149: 3-16.

[28]Sanjita Jaipuria, Mahapatra S S. An improved demand forecasting method to reduce bullwhip effect in supply chains[J]. Expert Systems with Applications, 2014, 41: 2395-2408.

[29]Kahn J A. Inventories and the volatility of production[J]. Am Econ Rev., 1987, 77(4): 667-679.

[30]Heyman D P, Sobel M J. Stochastic Models in Operations Research[M]. Vol. Ⅱ, New York: McGraw-Hill, 1984.

[31]Zinn W, Levy M, Bowersox D J. Measuring the effect of inventory centralization/decentralization on aggregate safety stock: The “square root law” revisited[J]. J. Bus Logist, 1989, 10(1): 1-14.

[32]Simchi-Levi D, Kaminsky P, Simchi-Levi E. Designing and Managing the Supply Chain: Concepts, Strategies, and Case Studies[M]. Boston: McGraw-Hill, 2000.

[33]Silver E, Peterson R. Decision Systems for Inventory Management and Production Planning[M]. 2ndedition. New York: John Wiley and Sons, 1985.

Reducing bullwhip effect in supply chain: A portfolio management approach

CHENChang-bin1,2,SHENGXin3*,LIANGYong-yi3

1. Research Centre for Modern Logistics, Tsinghua University, Beijing 100083, China;2. Zhongshan Institute, University of Electronic Science and Technology of China, Zhongshan 528402, China;3. Lingnan College, Sun Yat-sen University, Guangzhou 510275, China

In the supply chain system comprising of one supplier and several retailers, retailers are likely to face two kinds of market demand in a dynamic environment: demand under no sales promotion and demand under sales promotion. In this situation, we assume that the retailers adopt the order-up-to level policy to play orders from suppliers according to the information of market demand. On the other hand, the retailers in the same market may take each other’s order-decision behavior into account. In this article, we discuss the downstream suppliers’ decisions of ordering from upstream suppliers when retailers have different correlations. Furthermore, we investigate the retailers leveraging the portfolio management approach from securities investment theory to adjust the retailers’ quantity of ordering which can reduce the total variance of ordering to suppliers and the bullwhip effect. And we investigate the retailers’ motivation on order adjustment by analyzing and comparing inventory cost, loss of out of stock and profit which the inventory level before and after order adjustment. Our numerical findings show that portfolio management approach can help to reduce the total variance of ordering to the supplier. Also, this method can reduce the bullwhip effect in the supply chain to some extent when multiple retailers have different correlation coefficients of the decision-making behavior in the same market. The greater the correlation coefficient among the retailers is, the more significant the effect on eliminating the bullwhip effect in supply chain will be. Moreover, at the same correlation coefficient, the greater the variance of the market demand forecasted by the retailers, the greater the effect on reducing the bullwhip effect is with the application of the portfolio management approach.

supply chain; order-up-to level policy; bullwhip effect; portfolio management approach

① 2013-06-19；

2014-10-03.

广东省自然科学基金资助项目(2014A030313643)； 浙江省科技计划一般软科学资助项目 (2010C35004)； 浙江省教育厅资助重点项目(Z200908711)； 杭州市哲学社会科学重点研究基地资助项目(2012JD26)； 杭州市科技计划软科学资助项目(20110934M29)； 浙江省社会科学界联合会“民生调研协作攻关”专项课题资助项目(2011XN03).

盛鑫(1982—)， 男， 安徽亳州人， 讲师， 博士. Email: shengxinzsu@163.com

F270

A

1007-9807(2016)06-0033-16