已实现跳跃波动与中国股市风险溢价研究——基于股票组合视角①

陈国进, 刘晓群, 谢沛霖, 赵向琴

(1. 厦门大学王亚南经济研究院, 厦门 361005; 2. 厦门大学经济学院金融系， 厦门 361005；3. 海南大学旅游学院， 海口 570228)



已实现跳跃波动与中国股市风险溢价研究
——基于股票组合视角①

陈国进1, 2, 刘晓群3, 谢沛霖1, 2, 赵向琴2*

(1. 厦门大学王亚南经济研究院, 厦门 361005; 2. 厦门大学经济学院金融系， 厦门 361005；3. 海南大学旅游学院， 海口 570228)

基于我国股市5分钟高频数据为研究样本, 采用非参数方法估计了Fama-French25个股票组合的已实现跳跃波动率的主要成分(规模、均值、标准差和到达率等)，实证分析表明：(1)已实现跳跃波动的主要成分可通过线性和非线性(交叉项)形式预测大部分股票组合的超额收益率.(2)已实现跳跃波动率成分在一定程度上可以通过线性方式解释股票组合的横截面收益.(3)已实现跳跃波动率可能是Fama-French三因子模型中规模因子和账面市值比因子的背后驱动因素.

股票组合风险溢价; 已实现跳跃波动率; Fama-French三因子模型

F830.9; F830.59; F832.5

A

1007-9807(2016)06-0098-16

0　引　言

跳跃是股票价格运动中的重要现象，往往包含着重要的信息，因而在金融学中受到了广泛的关注.而对于跳跃波动率的估计包括参数方法和非参数方法.一方面，在参数模型中，跳跃序列的获取比较复杂，且跳跃主要通过间接方式解释和预测风险溢价，如Drechsler[1]发现跳跃到达率和跳跃规模会影响到方差风险溢价，Maheu等[2]将跳跃到达率、跳跃均值和方差以非线性形式嵌入到条件方差、条件偏度和条件峰度动态方程中，通过两成分GARCH-跳跃扩散模型间接估计了跳跃对股权溢价的影响.

另一方面，Barndorff-Nielsen和 Shephard[3-5]发展出基于双幂方差的非参数高频方法来估计已实现跳跃波动率，在估计已实现跳跃波动率时无需假定股票价格运动的具体表达形式.Andersen等[6]、Huang 和 Tauchen[7]认为基于非参数方法可以更精确估计已实现跳跃波动率，并分析了已实现波动率中的连续成分和跳跃成分在解释风险溢价上的不同贡献.Todorov和Bollerslev[8]使用市值最大四十只个股及其组合的跳跃波动率，发现已实现跳跃波动率与连续波动率在解释风险溢价方面的贡献显著不同.

进一步地，Tauchen等[9]提出了一个以市场风险、长期跳跃波动率风险和短期跳跃波动率风险构成的三因子模型，与Fama-French三因子模型相比，该模型的定价偏误更低，长期跳跃波动率和短期跳跃波动率对风险溢价有不同的贡献，并且认为长期跳跃波动率源于整体宏观经济的变动，而短期跳跃波动率与公司微观层面的融资约束密切相关.Tauchen等[9]证实，基于股市指数估计的已实现跳跃波动率的规模、均值、到达率和方差等参数对信用违约掉期利差具有显著的解释能力；Guo等[10]选取S&P500指数探讨已实现跳跃成分与风险溢价之间的关系.国内文献中，陈国进等[11]、左浩苗等[12]、牛华伟[13]、赵秀娟等[14]、黄冉等[15]也研究了跳跃波动率在资产定价和风险管理中的作用.

那么，如何从经济学角度去解释跳跃波动率的风险溢价呢？基于灾难风险的资产定价模型为探讨跳跃波动率的风险溢价提供了一种理论解释[16, 17].这里的灾难风险是指发生概率很小，但是一旦发生会造成很大损失的灾难性事件冲击.灾难风险主要通过两种渠道影响到风险溢价，一是灾难实际发生造成实体经济的重大损害，进而传递到股票市场，二是投资者对灾难风险的预期，即使灾难风险实际上没有发生，投资者基于历史上发生灾难的认知，担心未来灾难可能发生，从而要求有一个更高的风险溢价.而基于高频数据跳跃波动率和基于个股横截面尾部风险是估计我国股市罕见灾难风险的重要方法.

Bollerslev等[18]基于跳跃尾部风险构造了投资者恐慌指数，发现投资者规避灾难风险是导致跳跃波动率风险溢价的主要原因.Kelly等[19]认为基于个股横截面数据估计的股市尾部风险，可以较好解释美国股市横截面收益的差异性.陈国进等[20]参考Kelly等的方法，利用我国个股横截面日收益率数据提取尾部风险，作为灾难风险的度量，根据尾部风险因子载荷系数大小将股票资产分成5个股票组合，实证研究发现高尾部风险载荷系数的股票组合收益率显著大于低尾部风险载荷系数股票组合的收益率.

在现有文献中，对已实现跳跃波动率风险的研究主要是使用市场综合指数或大公司个股[21-23]，尚缺乏对股票组合的分析，一个可能的原因是，相对于指数和个股序列，通过滚动方法动态构造股票组合来估计跳跃风险比较复杂和繁琐.本文将采用非参数方法，利用我国股市A股5分钟高频数据，来估计股票组合的已实现跳跃波动率主要成分(包括跳跃规模、均值、方差、到达率等)，实证分析已实现跳跃波动率主要成分对股票组合收益的预测和解释能力，并进一步分析已实现跳跃波动率主要成分与Fama-French三因子模型中规模因子和账面市值比因子之间的内在联系，弥补这一领域的研究空缺.

1　已实现跳跃波动率成分估计： 非

参数方法

使用高频数据非参数估计方法识别已实现跳跃波动率，一个隐含的前提是股票市场的跳跃极少发生(如一个交易日里最多只算发生一次跳跃)，但是一旦跳跃发生，它将对股市收益率产生很大的影响.

假设对数股票价格pt=ln(Pt)服从一个跳跃扩散过程

dpt=μtdt+σtdWt+Jtdqt

(1)

dqt是一个泊松跳跃过程，强度(跳跃率)为λJ，Jt是相应对数跳跃规模的分布，服从正态分布N(μJ，σJ)；

根据Andersen和Bollerslev[24]对已实现波动率的计算方法，假定一个交易日t，将每日的交易分割为M段，Pt,j表示交易日t中第j个收盘价，j=1,2，…，M.令rt,j为交易日t内第j时段的对数收益率，rt,j=lnPt,j-lnPt,j-1.交易日t的已实现波动率(RVt)可以表示为

(2)

在现实股票市场中，由于市场受较大的信息冲击和投资者非理性因素的影响，金融资产的价格波动不再是连续的，而存在跳跃性波动.为分离出离散跳跃方差，Barndorff-Nielsen和Shephard[4, 5]提出了已实现双幂次变差(realized bipower variation，BV)，即

(3)

(4)

进一步使用Barndorff-Nielsen和Shephard[4]、Huang和Tauchen[7]在二次双幂次变差理论基础上提出的Zt统计量来鉴别离散跳跃方差成分，以提高离散跳跃方差的计算精度.Zt统计量的表示形式如下式

(5)

其中

(6)

在1-α的显著性水平下，可以得到离散跳跃方差的估计量为

(7)

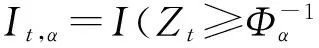
Size_RJVmonth=∑Size_RJVday

(8)

Mean_RJVmonth=Size_RJVmonth/N_RJV_days

(9)

Arr_RJVmonth=N_RJV_days/days

(10)

Std_RJVmonth=

(11)

其中 N_RJV_days为一个月里跳跃发生的天数，days为该月总天数，Size_RJVmonth为一个月里所有组合成分日已实现跳跃规模的平均值，Arr_RJVmonth为一个月里跳跃的强度或到达率，它随着所选的置信水平α的不同而不同.在实际操作过程中，需要选取合适的α，Tauchen和Zhao[9]发现在跳跃贡献度分别为10%和80%时，置信水平分别为0.99和0.999，这样通过选择合适的跳跃风险检验水平，可以得到精确的参数估计值，并随样本规模的增大而收敛，在本文中根据以往中国股市的特征研究，置信水平α选取0.95[12].

2　数据来源及股票组合跳跃波动率

成分的描述性统计

2.1数据来源

日内数据的抽样频率对研究结果影响较大，一方面，抽样频率太低，不能很好地刻画当天波动信息；另一方面，抽样频率太高，会产生微观噪音进而影响研究结果.因此，本文兼顾这两方面的影响，采用中国股票市场综合A股指数和其所有成分股5分钟高频数据作为研究跳跃成分的样本，数据来源于国泰安高频金融数据库.样本的时间跨度为2007年1月4日至2013年12月31日，共84个月，每天49个交易数据(包括1个隔夜交易数据和48个日内交易数据).以月频率来进行研究，25组合的流通市值加权月收益率数据来源于锐思数据库，月已实现跳跃成分由每组的日数据加总后得到月数据.本文中估计的RV、BV、Arr_RJV、Size_RJV、Mean_RJV、Std _RJV等变量均由SAS 9.3软件处理得到.

2.2股票组合构建

本文参考Fama-French股票组合的构建方法，根据规模与账面市值比构建25个股票组合，分组方法为：公司规模用T年6月末的市值代表，公司账面市值比用T-1年会计年度股权的账面价值除以T-1年12月末的市值；分别取市值及账面市值比的五等分点，两个五等分点相交，将所有的股票分为25组.完成25个股票组合的分组后，计算每个股票组合T年7月到T+1年6月每月按照流通市值作为权重的加权平均收益率.

样本区间为2007年～2013年共7年，每一年有25个组合，参考Fama-French滚动构建股票组合的方法，构成的这25组中成分股是可能发生变化的.以每一年25组中每一组中成分股的高频5分钟数据计算出每只股票每日频率RJV的大小、均值、标准差、到达率，并简单相加得到每只股票的12个月度频率跳跃数据，再将这些股票进行简单平均最终得到该组合在这一年的12个月度跳跃成分数据.综合7年数据，相应25个组合的四个跳跃成分每一年的12个数据组合在一起，构成84个数据的时间序列.值得注意的是，构成每一个组合的股票在每一年里可能会发生变化，但是每个组合包含的特征没有发生变化，本文关心的是s1b1...s1b5, s2b1…s2b5,…,s5b1…s5b5这25个组合(s1-s5是规模市值由低到高，b1-b5是账面市值比由低到高，s1b1为市值规模最小且账面市值比最小的股票组合，s5b5为市值规模最大且账面市值比最高的股票组合)在这7年里各自以组合这个整体表现形式在12个月的跳跃值的变化.所以，2007年计算25个组合跳跃值的成分股在2008年时，又是通过25组合不同的成分股来计算跳跃值，以此类推至2013，虽然每一年的成分股是不一样的，但仍反应出7年里25个组合的时变已实现跳跃波动率(RJV).简而言之，使用7年组合成分股计算每一年的月频率RJV，最后整合在一起构成84个月的84个RJV序列作为本文所需要的跳跃变量.

表1A至表1E概括了样本区间内股票组合平均收益率(Portfolio_Return)和已实现跳跃规模(Size_RJV)、均值(Mean_RJV)、达到率(Arr_RJV)和标准差(Std_RJV)的均值，Jarque-Bera值以概率的形式用星号给出，可以看出已实现跳跃成分序列表现出明显的“尖峰厚尾”，不服从正态分布.

同时可以看出，25个组合的跳跃规模(Size_RJV)约为9%，所有个股组合的跳跃均值(Mean_RJV)约为2.3%，跳跃标准差(Std_RJV)约为0.45%，跳跃到达率(Arriving Rate，Arr_RJV)为19%左右.Tauchen和Zhou[9]认为股价指数、债券和外汇市场中Arr_RJV在10%-20%之间，作者的估计与Tauchen和Zhou[9]的估计基本一致.

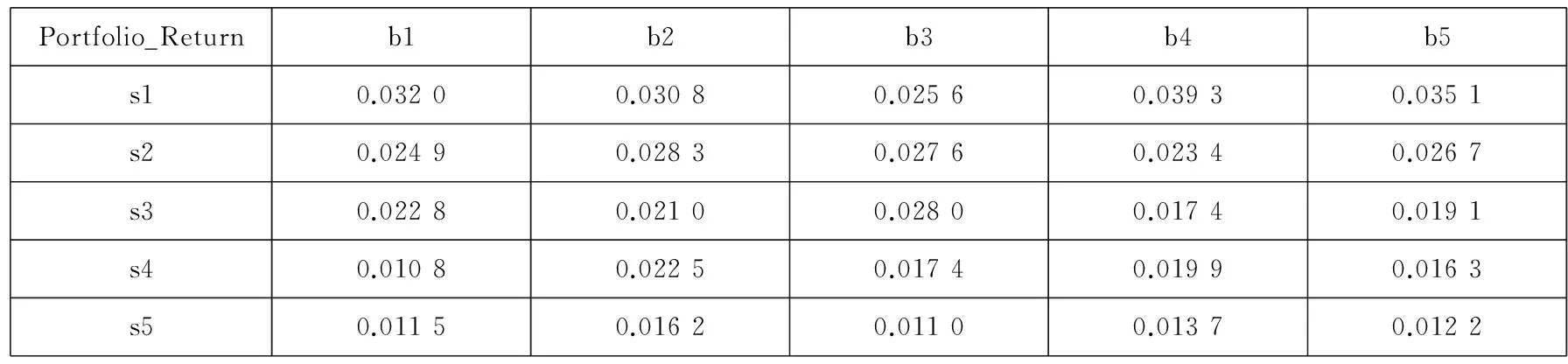
表1A Fama-French组合收益率的描述性统计

从表1A可以看出，我国股票市场也存在显著的规模效应，控制公司的账面市值比后，小公司收益显著高于大公司的收益.我国股票市场在一定程度上也存在价值股溢价效应，总体上价值股的收益率要高于成长股的收益率，虽然这种单调性不如公司规模效应明显.

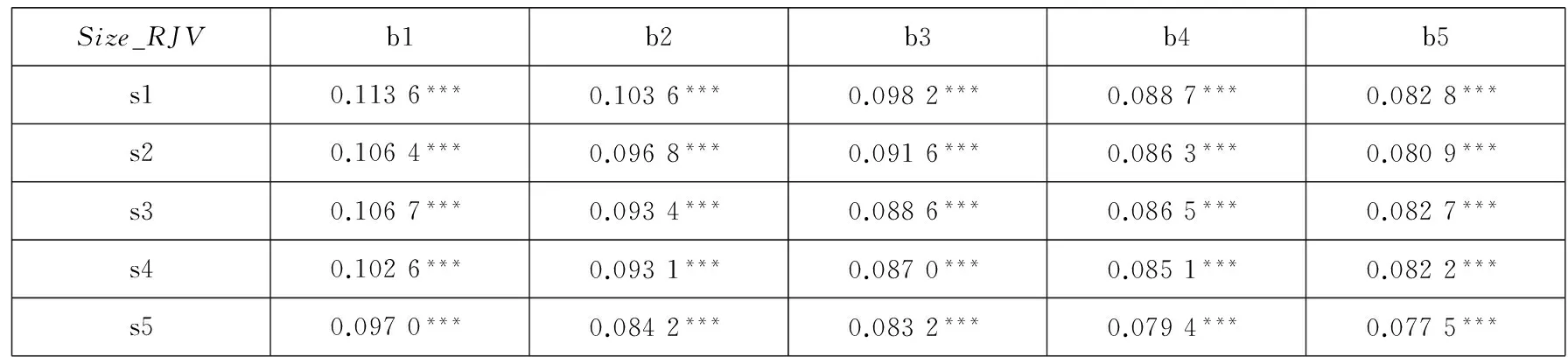
表1B　Fama-French组合跳跃规模(Size_RJV)的描述性统计

注: 表中***、**和*分别表示在1%、5%和10%的显著性水平下显著，下同.

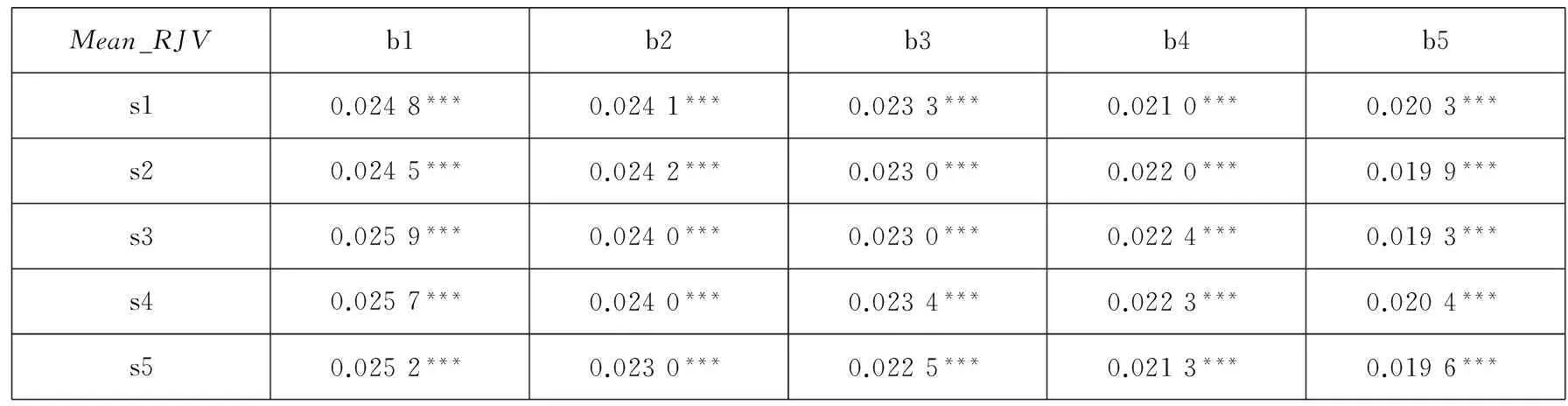
表1C　Fama-French组合跳跃均值(Mean_RJV)的描述性统计

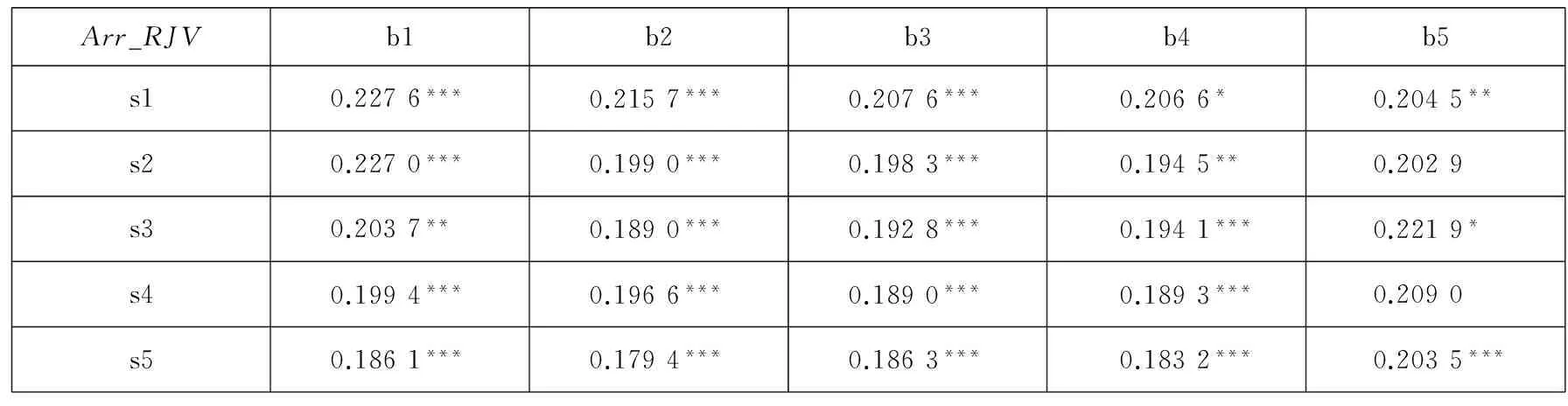
表1D　Fama-French组合跳跃到达率(Arr_RJV)的描述性统计

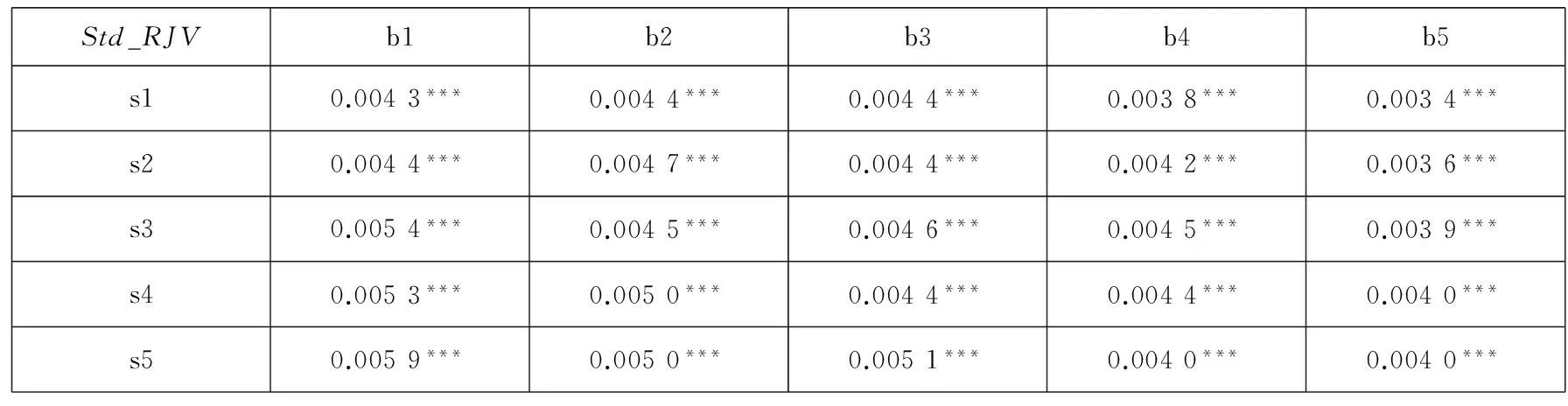
表1E　Fama-French组合跳跃标准差(Std_RJV)的描述性统计

从表1B到表1E给出的公司规模、公司账面市值比与跳跃波动率各个成分之间关系.总体而言，规模小的组合收益率高，Size_RJV和Arr_RJV也高，规模大的组合收益率低，Size_RJV和Arr_RJV变小，符合高收益率伴随着高风险，同时规模因子Size与Std_RJV有一个负相关的关系；而B/M小的组合收益率低，虽然不是有严格的递减趋势，一般来说，B/M在b1时收益率低于最大的b4和b5下的组合收益率，此时的Size_RJV和Mean_RJV与Std_RJV在b1时偏高，这意味着低账面市值比的组合获得相对较低的收益率，同时却面临着高风险，而高账面市值比的组合获得相对较高的收益率，同时却面临着相对较低的风险.

3　跳跃性波动与股票组合收益关系

分析

3.1已实现跳跃成分对超额组合收益率时序

分析

本文的主要关注点在于跳跃成分是否可以作为一个风险因子来预测和解释股票组合的超额收益率.对于跳跃成分以何种形式引入方程，Bali等[25]使用高频数据实证探讨收益-风险权衡关系的建模思路，Zhang等[26]用已实现跳跃成分之间的简单线性关系建模，Heston等[27]及Nijman等[28]在分析平均组合收益率时使用变量之间的交叉项，Maheu等[2]在参数框架下以非线性的方式将跳跃到达率和跳跃分布参数的均值及方差嵌入到条件方差、条件偏度和条件峰度，间接探讨时变跳跃对股权溢价动态性的作用，参考以上做法，将跳跃成分同时以线性和交叉项的非线性方式进入方程来解释和预测组合超额收益率.由此，提出以下对股票组合市场超额收益率的预测回归方程

ri,t+1-rf,t=C+βMKT(rM,t-rf,t)+βi,SizeSizet+

βi,MeanMeant+βi,StdStdt+βi,ArrArrt+

γi,SASizet*Arrt+γi,STDAStdt*Arrt+

…+βM,SizeMSizet+βM,MeanMMeant+

βM,ArrMArrt+βM,StdMStdt+ζi,t+1

(12)

式(12)即对25组合进行第一阶段Horse-Races时序实证分析的回归方程，其中i为股票组合，为简化起见,组合已实现跳跃的大小、均值、标准差和到达率分别用Size、Mean、Std、Arr表示，同样的，MSize、MMean、MStd、MArr分别是市场指数已实现跳跃成分，包括市场指数已实现跳跃的大小、均值、标准差和到达率，省略号(…)代表其它可能的八种交叉项，t为月频率，ri,t+1-rf,t为股票组合超额收益率，rM,t-rf,t为市场超额收益率.式(12)也是下面使用Fama-MacBeth两步回归法深入分析跳跃与股票组合收益关系的基础.

先使用方程(12)初步验证跳跃风险与股票组合超额收益率之间的关系，考虑组合本身的跳跃成分，并将代表系统性风险的市场跳跃波动作为控制变量，能更精确探讨股票组合本身特质性的非系统风险对其超额收益率的影响.使用Horse_Races 回归方法进行估计，相对于OLS回归方法，此方法更加直接.

通过Horse_Races回归逐步剔除最不显著变量，最终仅保留所有显著变量的结果显示：25个组合中有19个组合的跳跃成分以线性和非线性的形式显著，调整拟合优度值达到0.6-0.8，解释和预测了一部分超额收益率，具体结果见表2A和表2B的s1bi和s2bi，其余由于篇幅所限不再一一列出.

表2A　基于组合跳跃成分和市场跳跃成分向前一期预测s1bi 组合超额收益率

注：表中为Horse_races回归保留下的所有显著变量，在交叉项变量中，S、M和A分别为已实现跳跃规模Size_RJV、均值Mean_RJV和到达率Arr_RJV的简写，下同.

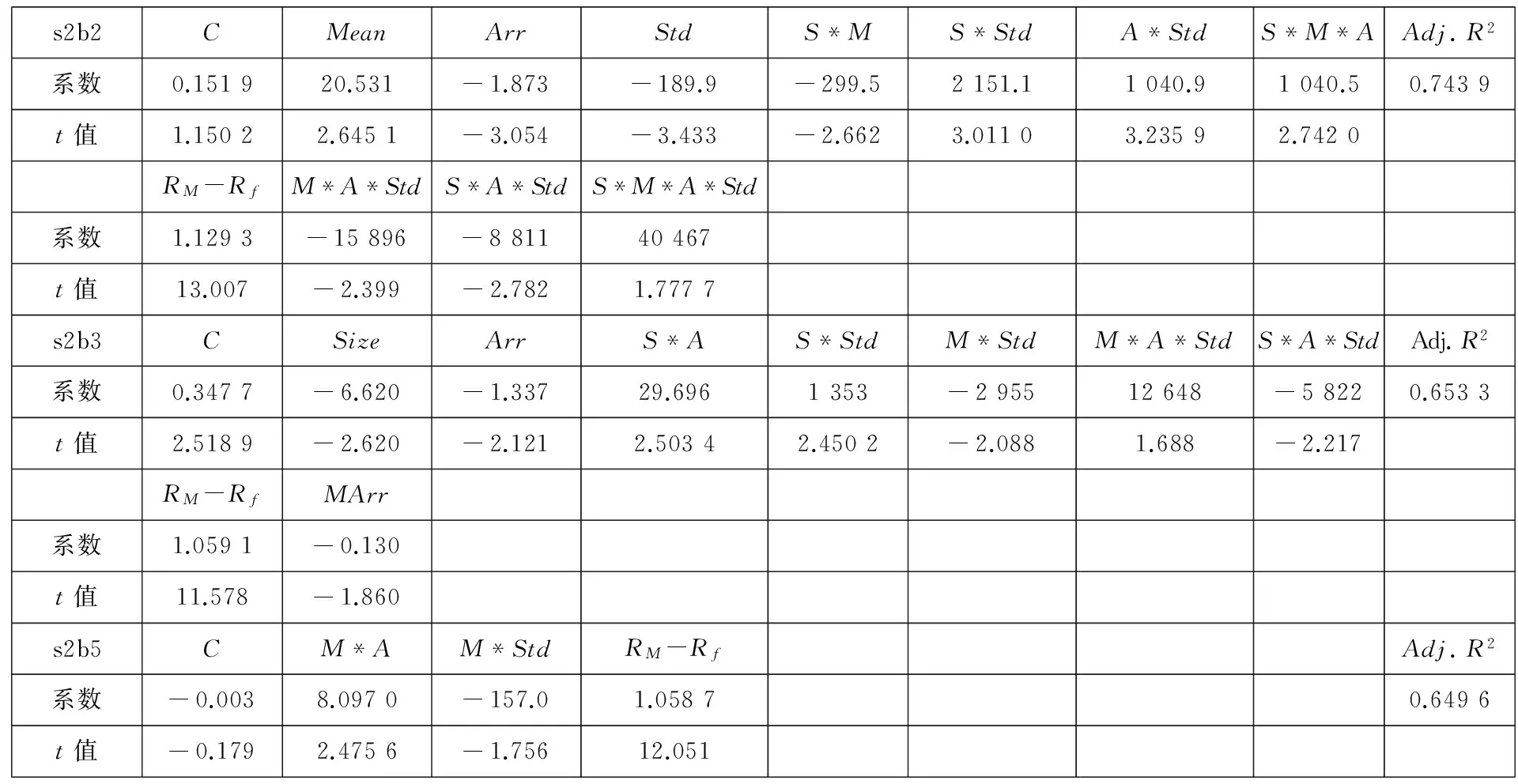
表2B　基于组合跳跃成分和市场跳跃成分向前一期预测s2bi 组合超额收益率

在Horse_Races时序分析中比较显著的一些跳跃变量的系数有出现负值，Lettau和Ludvigson[29]也得到波动率与风险溢价之间负的或不显著的关系.一个可能的解释是特质波动率与收益率序列之间的反向关系，因为公司层面特质波动率的研究也是从偏度、融资约束、投资者风险厌恶等不完全市场理论进行分析的.

3.2已实现跳跃成分与超额组合收益率横截面

分析

上述的Horse_Races时序回归初步得出了影响每个组合的线性和非线性跳跃解释因子.接下来分别以19个显著组合的解释变量为共同风险因子，进行19次Fama-MacBeth两步回归，深入探讨横截面风险收益权衡关系.从以下三个方面进行分析：

第一，总结出以哪一个组合的解释变量进行Fama-MacBeth第一步时序回归时，其它24个组合在同样的解释变量下也存在在统计和经济意义上都显著的相同变量；第二，以其中一个组合的解释变量进行回归时，其它哪些组合最大程度在这些变量上也显著，即这些组合不仅有其自身通过Horse_Races方法得出的显著解释变量，在使用其它组合形成的解释变量时也是显著的，这隐含着，一方面可以探讨这两个及以上组合解释变量之间的规律，另一方面可以探讨横截面不同特征组合在风险因子上的共同规律.第三，Fama-MacBeth第二步回归，得出解释横截面风险溢价的线性和非线性跳跃因子.

具体说来，以s1b1为例，在Fama-MacBeth第一步回归中，s1b1在Horse-Races回归中得出的显著解释变量Mean_RJV、Arr_RJV、Mean*Arr、Arr*Std、Mean*Arr*Std、RM-Rf和MSize作为所有25组合的回归变量，建立如下方程

在Fama-MacBeth第二步截面回归中，

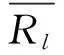
依次类推，分别以余下18个组合在时序Horse-Races回归中的显著解释变量作为Fama-MacBeth第一步回归中共有解释变量，再进行第二步截面回归，进行18次.

下面分开阐述以上三个问题的回归结果：

1)所有19次Fama-MacBeth第一步时序回归中，当以s1b1的Mean_RJV、Arr_RJV、Mean*Arr、Arr*Std、Mean*Arr*Std、RM-Rf和MSize为解释因子时，另有17个组合此时的时序回归中，有相应的跳跃成分是显著的；以s3b4的Size_RJV、Mean_RJV、Arr_RJV、Size*Mean、Size*Arr、Size*Std、Mean*Arr、Arr*Std、Size*Mean*Arr、Mean*Arr*Std和RM-Rf为解释因子时，另有18个组合有相应的跳跃成分是显著的，且它们调整拟合优度值可达到0.60-0.80；s4b5、s3b3和s1b5分别有14、13和11个显著；余下的组合都有相对应显著的其它组合，但个数只有3到9个不等.

2)由1)得出以组合s3b4、s1b1、s4b5、s3b3、s1b5在Horse-Races回归中的解释变量为余下组合的解释变量时，显著的组合最多，因而主要分析它们的结果，由于篇幅所限，这里只列出s1b1和s1b5的结果，即表3A～表3B.

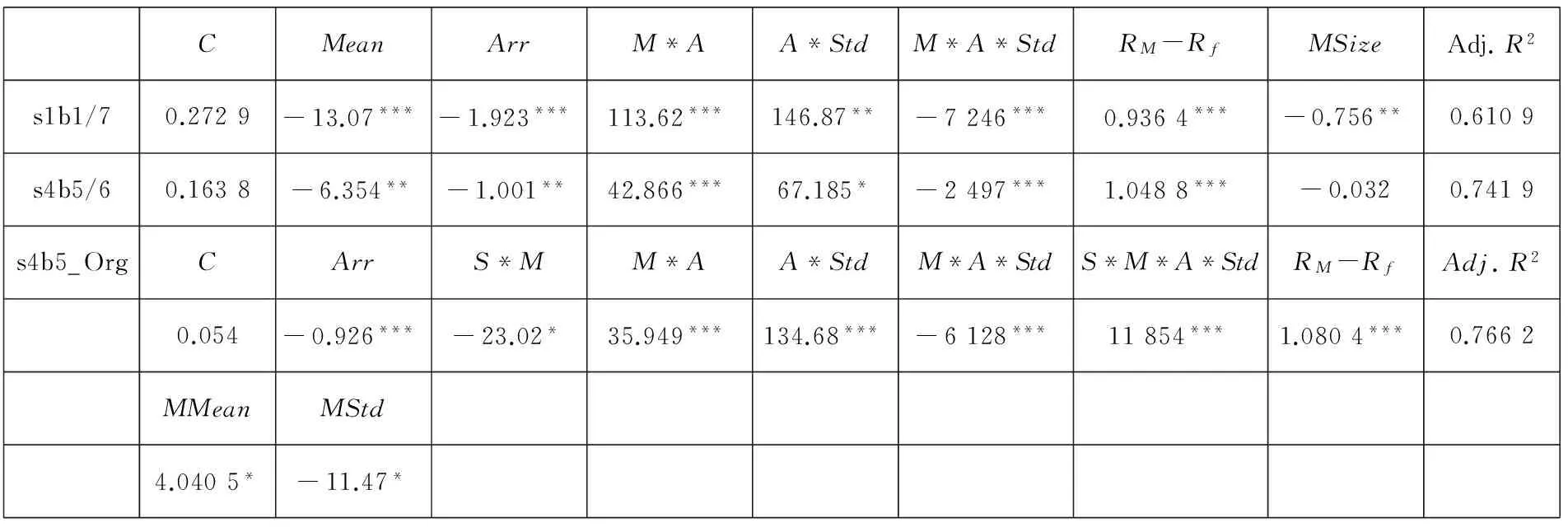
表3A　s1b1及其它组合解释变量系数

注：表中s1b1/7代表s1b1在Horse_Races回归中的7个解释变量，且都是显著的；s4b5/6代表s4b5在s1b1中的7个变量中有6个是显著的；s4b5_Org为s4b5在自身Horse_Races回归时得出的显著变量，下同.

表3B　s1b5及其它组合解释变量系

从回归结果，可以发现s1b1在Horse_Races回归时有6个变量是显著的，此时的s4b5和s1b3在这个变量中都有6个显著.以s4b5为例，它自身的Horse_Races回归有同样的Arr_RJV、Mean*Arr、Arr*Std、Mean*Arr*Std显著，且系数符号与s1b1一致；s1b5时有9个显著变量，s2b2同样9个变量都显著，这与s2b2自身的Horse_Races回归，其显著变量有12个有密切联系，可以看出共同显著的变量有Arr_RJV、Size*Mean、Size*Std、Size*Mean*Arr、Size*Arr*Std，且符号一致.

3)对所有19个解释变量组进行19次Fama-MacBeth第二步截面回归，结果显示与第一步时序回归接近一致：s1b1，s2b2，s3b4，s4b5的截面回归结果较好.由表4A～表4D可以发现，以s3b4的解释变量为其它所有24组的回归因子时，所有线性和非线性的已实现跳跃成分因子都是显著的，且β系数为正，其中已实现跳跃到达率(Arr_RJV)在这三组以及s2b2中都显著且系数值最大，已实现跳跃均值(Mean_RJV)在这四组中也是显著的，同时交叉项的跳跃成分显著，但系数值偏低，说明对于横截面组合收益率，跳跃风险主要还是以线性方式产生作用.

表4A　以s1b1的解释变量作为Fama-MacBeth共同回归因子时的横截面回归结

表4B　以s2b2的解释变量作为Fama-MacBeth共同回归因子时的横截面回归结

表4C　以s3b4的解释变量作为Fama-MacBeth共同回归因子时的横截面回归结果

表4D　以s4b5的解释变量作为Fama-MacBeth共同回归因子时的横截面回归结

总之，由截面回归结果，已实现跳跃成分获得正的风险溢酬，意味着非线性组合形式的已实现跳跃成分能作为解释横截面收益的重要风险来源，这与现有基于消费的灾难风险模型所强调的一致：投资者害怕未来消费增长和股票市场收益中负向跳跃的出现，因而要求获得相应的风险溢价[30].

4　已实现跳跃成分与公司规模、账

面市值比关系的进一步分析

众所周知，Fama-French的三因子模型是用来解释股市横截面收益差异性的最主要实证模型之一，但是为什么公司规模和账面市值比可以作为共同因子，在学术界并没有获得一致的认识.考虑到跳跃是股票价格出现较大且低频率发生的变动，将跳跃风险作为投资者对重大信息冲击做出的反应，已实现跳跃波动成分是否与公司规模效应和账面市值比效应存在某种关系？下面将进一步探讨这个问题.

Yan[31]以及Jiang和Yao[32]对公司特征因子加以控制，分别在期权市场和股票市场探讨了跳跃对股票收益率预测能力.参考这些文献，在式(12)的基础上，分析跳跃波动率风险可以作为横截面收益的风险因子的背后原因：加入Fama-French的规模因子(SMB)和账面价值比因子(HML)，从这两个公司特征因子与跳跃波动之间是否存在联系的角度探讨跳跃波动率风险可能包含的信息.回归方程(式13)和Fama-French三因子模型(式14)分别为

ri,t+1-rf,t=C+βMKT(rM,t+1-rf,t)+γSMBSMBt+1+

γHMLHMLt+1+βi,SizeSizet+βi,MeanMeant+

βi,StdStdt+βi,ArrArrt+γi,SASizet*Arrt+

γi,STDAStdt*Arrt+…+βM,SizeMSizet+

βM,MeanMMeant+βM,ArrMArrt+

βM,StdMStdt+ζi,t+1

(13)

ri,t-rf,t=C+βMKT(rM,t-rf,t)+γSMBSMBt+

γHMLHMLt+ζi,t

(14)

如果在加入SMB和HML后不改变式(12)中跳跃成分的显著性，且这两个因子的γSMB和γHML变得不显著(在简单的三因子模型里，两系数是显著的)，意味着跳跃因子可能包含着规模效应和账面市值比效应的信息.

接下来首先在直观统计数据上，从规模效应和账面市值比两方面对收益率与跳跃成分之间的关系进行分析.对于规模效应, 固定股票组合的B/M，分析不同市值下的股票组合收益率与跳跃波动率的变化情况；同理，对于B/M 效应，固定股票组合的规模，分析不同B/M下的组合收益率与跳跃波动率的变化情况.再次，使用式(13)作进一步的实证检验.发现跳跃波动率可能包含着公司特征信息，跳跃波动率可能是Fama-French三因子模型中规模因子和账面市值比因子对横截面收益具有解释能力的背后驱动因素，投资者对信息冲击做出反应而导致的跳跃是需要被定价的风险因子.

4.1跳跃成分与规模效应的直观分析

在所有b1，b2，b3，b4，b5一定的情况下，规模小的组合Size_RJV和Arr_RJV高，收益率也高，规模大的组合Size_RJV和Arr_RJV变小，收益率大，高收益率伴随着高风险，这也与Fama和French股票组合的平均收益率与公司规模成反向关系结论相一致.表5为控制账面市值比因子后不同公司规模下收益率和跳跃风险之间的关系.

对于规模效应，跳跃均值(Mean_RJV)在最低账面市值比(b5)水平下，呈现规模小收益高而Mean_RJV风险小的特征，一个可能的解释是：低账面市值比的成长型企业具有被投资者看好的预期前景，从而跳跃幅度已被提前锁定.而对于其它依次变大的账面市值比水平，满足高跳跃均值风险及高收益下的规模效应.

值得注意的是规模因子与Std_RJV有一个负相关的关系.图1为其中一个组合的平均收益率与Size_RJV和Arr_RJV及Std_RJV的直观图(表中跳跃变量的表示已去掉符合“RJV”，其它四个组合的图形基本类似，不再列出).鉴于跳跃方差与公司层面特质波动率产生的共通性，一个可能的解释是特质波动率与未来收益率之间存在负向关系.

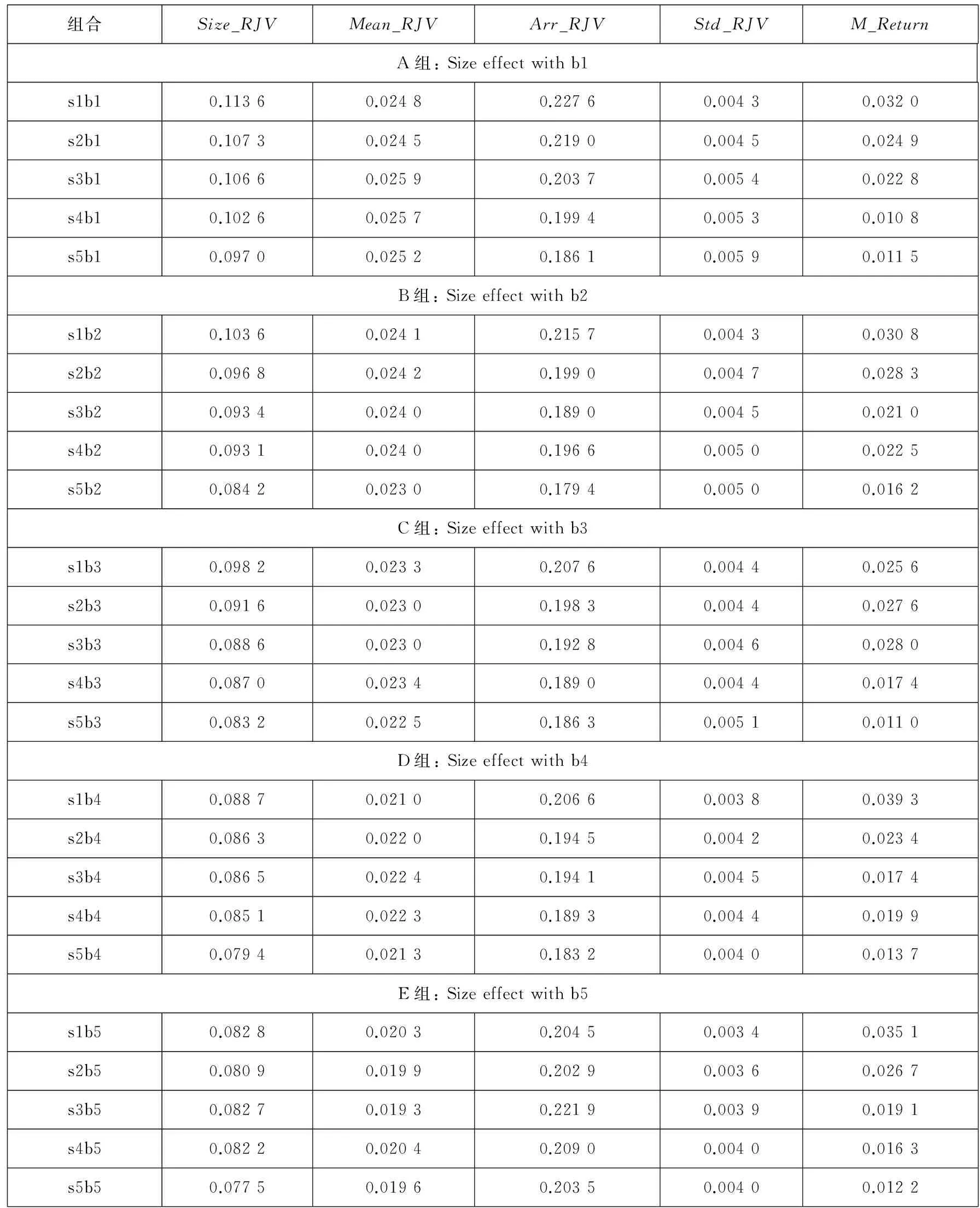
表5　规模效应下的平均跳跃成分与平均组合收益率

4.2跳跃成分与账面市值比效应的直观分析

图2为其中一个组合在控制规模因子和账面市值比因子后平均收益率与跳跃风险主要成分(Size_RJV和Mean_RJV及Std_RJV)之间关系的直观图(其它组合的图形基本类似，不再一一列出).从图2可以看出，我国股票市场在一定程度上存在账面市值比效应，但是随着账面市值比的上升，股票组合收益与账面市值比之间不存在严格的递减关系.此外，跳跃波动性成分Size_RJV和Mean_RJV及Std_RJV与公司账面市值比之间存在严格的递减关系.

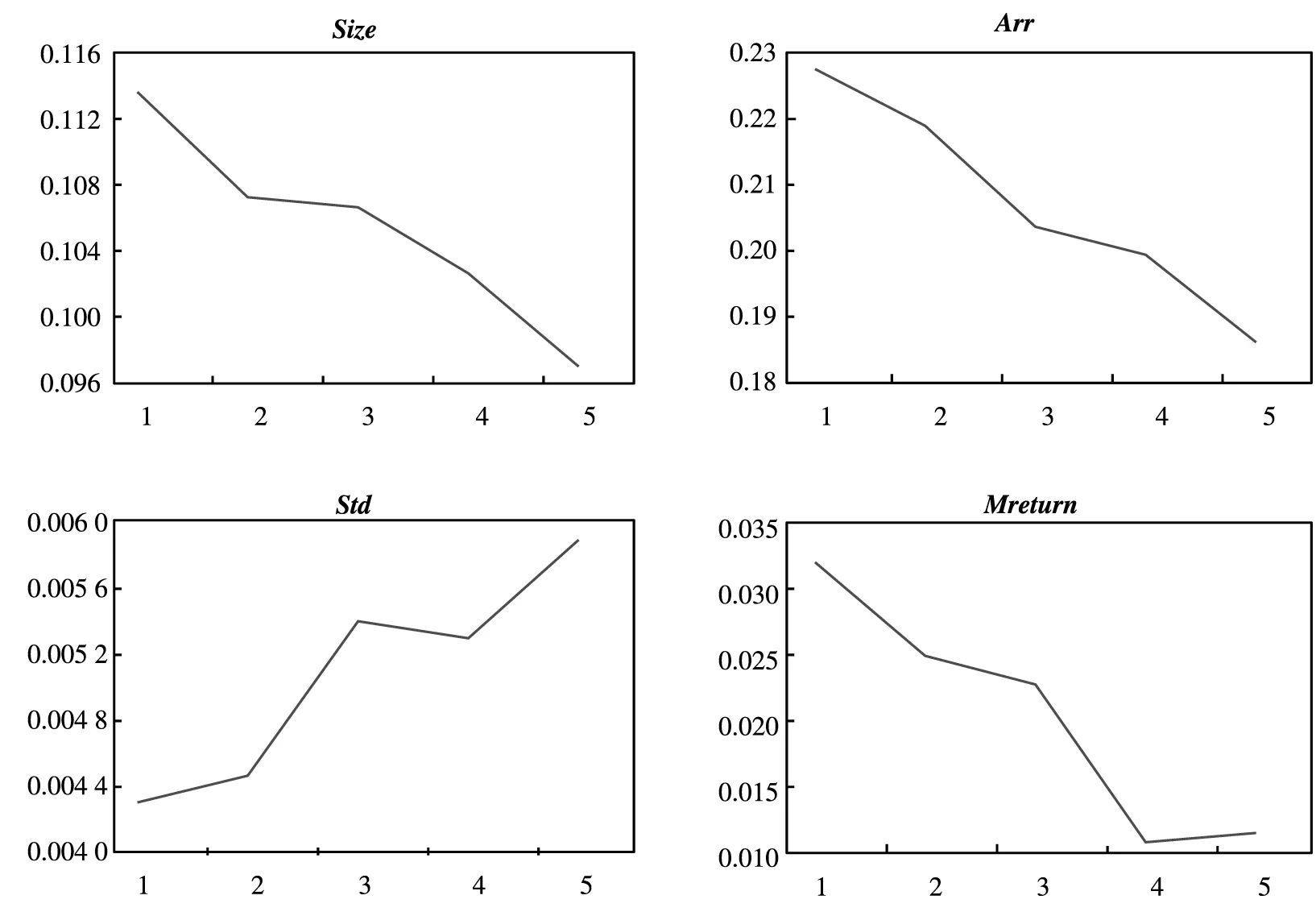
图1规模效应下组合收益率与跳跃成分关系

Fig.1 Portfolio return and jump components with different size

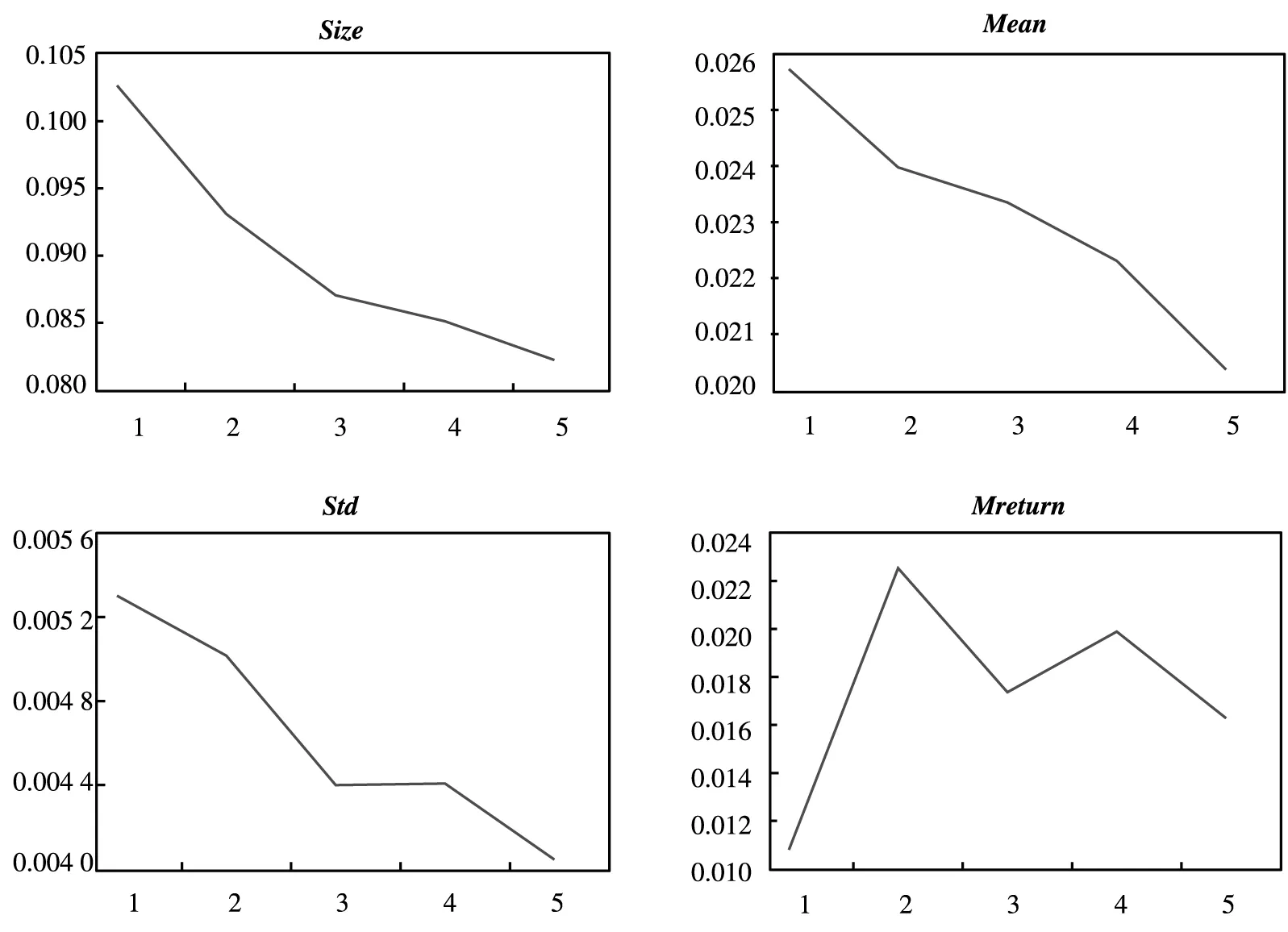
图2　价值溢价效应下组合收益率与跳跃成分

此外，跳跃到达率(Arr_RJV)仅在最小的两个规模水平(即固定s1和s2)，呈现单调的低账面市值比和高跳跃到达率风险、高账面市值比和低跳跃到达率风险变动，但是随着规模水平逐渐提高，Arr_RJV呈现W型，而组合平均收益率是呈现倒W型的(见图3)，价值溢价效应与跳跃到达率(Arr_RJV)似乎具有更紧密的联系.

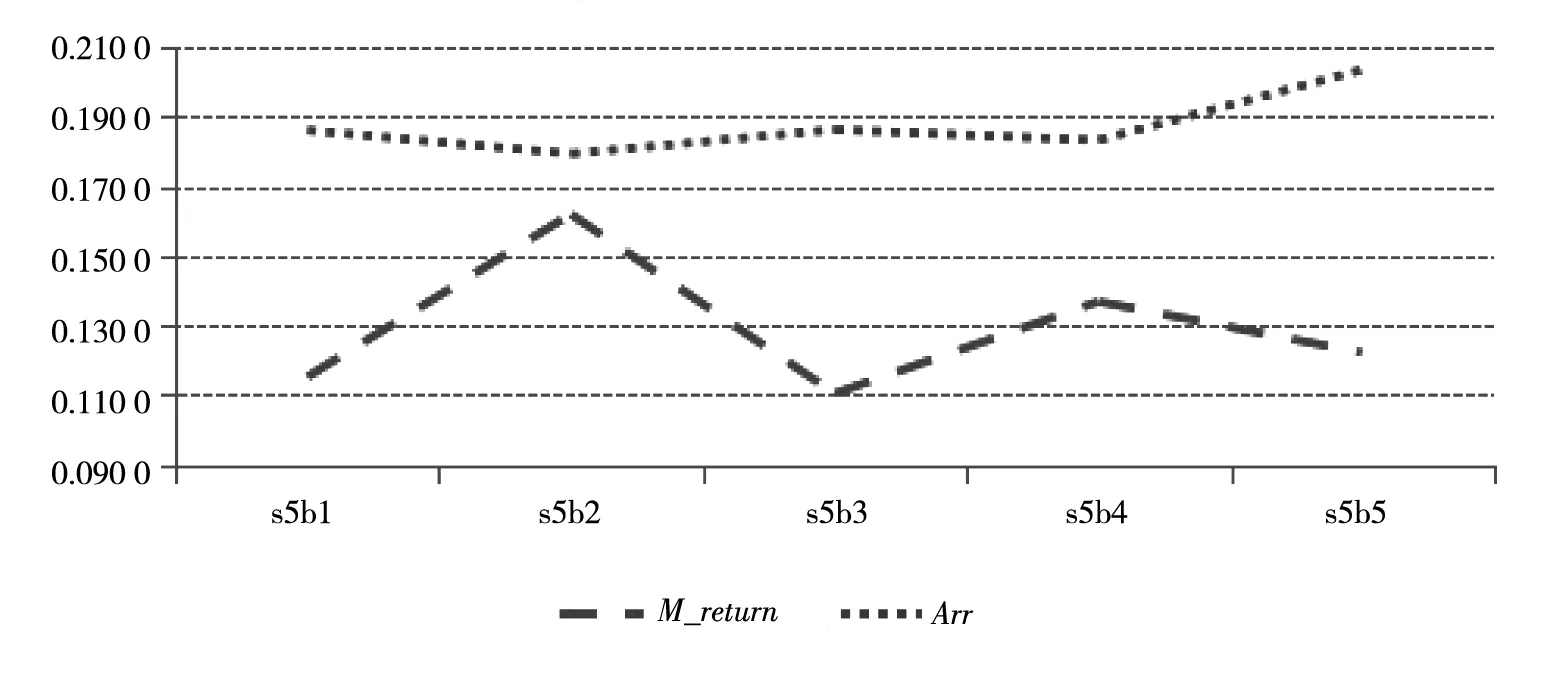
图3固定s5的价值溢价效应下组合收益率与跳跃到达率关系

Fig. 3 Portfolio return and Arr_RJV with s5 and different B/M

4.3跳跃成分和规模效应、账面市值比效应的回归分析

在上述得出的19个组合跳跃成分显著影响超额收益率的结论基础上，加入Fama-French模型的SMB和HML，运用式(13)回归的结果如表6所示(因为解释变量个数偏多，只列出FF因子的系数值和t值).

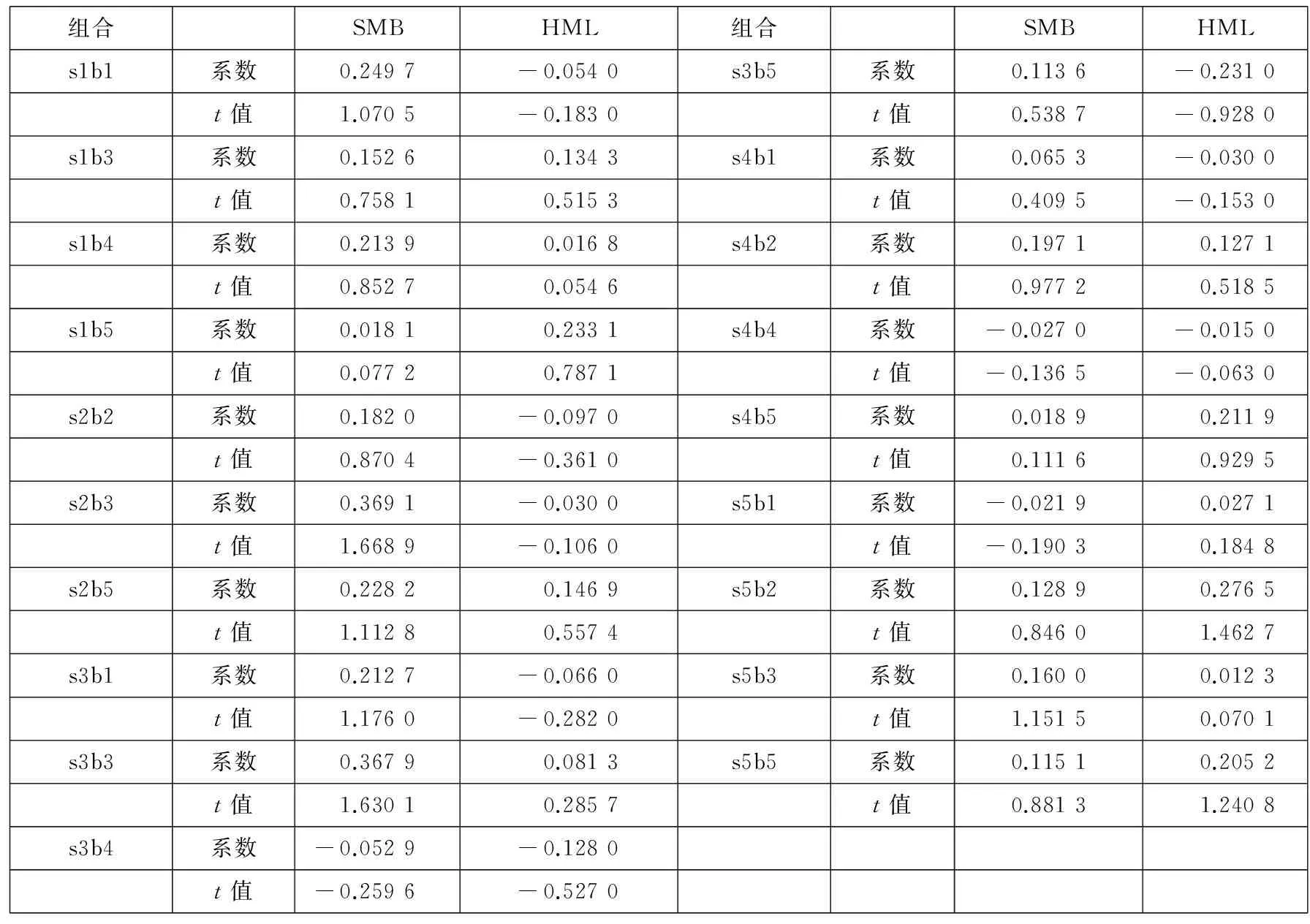
表6　基于已实现跳跃成分和FF因子的组合回归结果

全文中的影响依然显著，此时只有s2b3的SMB系数显著为正，且所有组合的调整拟合优度值有一定程度下降，说明跳跃波动性风险可能包含着规模和账面市值比所代表的信息，即投资者对引起公司股价出现跳跃的信息冲击的反应，可能是Fama-French公司特征因子模型的背后作用机理.

从以上分析可知，跳跃波动性风险各成份对企业特征(账面市值比与规模)的作用是不一样的.就B/M效应而言，跳跃规模、均值和标准差与账面市值比呈现简单的单调递减关系，而跳跃到达率对B/M的影响则更复杂，但也包含更多有用信息；就规模效应而言，则可以特别关注跳跃标准差的作用，它与特质波动率和特质偏度是高度相关的，对于跳跃标准差所代表风险与横截面收益的探讨，也许能为公司特质波动率之谜的分析提供新视角，这与郑振龙等[33]认为在资产定价模型中引入特质波动率风险因子有利于解释规模效应和价值溢价效应异象，以及特质偏度包含一部分特质波动率的信息基本一致.

5　结束语

在投资者对宏观未来不确定性担忧、重大事件可能发生的预期下，跳跃风险的存在会导致资产收益率分布的厚尾特征，这将影响到投资者风险信息的获取和对一个公司所面临风险的判断.若个股的非系统性风险无法被充分分散，那么在考虑个股层面和组合层面的收益率情况时，必须考虑这些风险带来的风险溢价问题.

本文用重大信息冲击驱动而导致跳跃的发生来度量尾部事件，采用非参数方法估计出已实现跳跃波动率及其反映其分布特征的规模大小、均值、标准差和到达率，探讨跳跃成分能否对横截面股票组合的风险溢价进行解释.

基于A股指数所有成分股5分钟高频数据，考虑Fama-French的规模因子和账面市值比因子作为控制变量，并按照规模和账面市值比确定的25组合，建立基于组合跳跃成分因子、市场指数跳跃成分因子的实证分析表明：

1)在时序分析上，已实现跳跃波动作为共同风险因子，对于股票组合的收益和风险溢价有一定的预测作用.Horse-Races分析中大部分组合(19个)的滞后一期跳跃成分同时以线性和交叉项的非线性形式来预测股票组合的超额收益率.

2)在横截面分析上，对所有19种解释变量组进行19次Fama-MacBeth第二步截面回归结果得出，特定组合的所有线性和非线性的已实现跳跃成分因子都是显著的，其中已实现跳跃到达率(Arr_RJV)的系数值最大，交叉项的跳跃成分显著，但系数值偏低，说明对于横截面组合收益率，跳跃风险主要还是以线性方式产生作用.

3)加入Fama-French三因子模型中的SMB和HML后，已实现跳跃成分对股票组合收益率的影响依然显著，且所有组合的调整拟合优度值有一定程度下降，说明跳跃波动性风险可能包含着规模和账面市值比所代表的信息，即投资者对引起公司股价出现跳跃的信息冲击的反应，可能是Fama-French公司特征因子模型的背后作用机理.

[1]Drechsler I. Uncertainty, time varying fear, and asset prices[J]. Journal of Finance, 2013, 68 (5): 1843-1889.

[2]Maheu J, McCurdyT, Zhao X. Do jumps contribute to the dynamics of the equity premium?[J]. Journal of Financial Economics, 2013, 110(2): 457-477.

[3]Barndorff-Nielsen E, Shephard N. Econometric analysis of realized volatility and its use in estimating stochastic volatility models[J]. Journal of Royal Statistical Society: Series B, 2002, 64(2): 253-280.

[4]Barndorff-Nielsen E, Shephard N. Power and bipower variation with stochastic volatility and jumps[J]. Journal of Financial Econometrics, 2004, 2(1): 1-37.

[5]Barndorff-Nielsen E, Shephard N. Econometrics of testing for jumps in financial economics using bipower variation[J]. Journal of Financial Econometrics, 2006, 4(4): 1-30.

[6]Andersen T, Bollerslev T, Diebold F. Some like it smooth, and some like it rough: Untangling continuous and jump components in measuring, modeling, and forecasting asset return volatility[R]. Working Paper, Philadelphia: University of Pennsylvania, 2003.

[7]Huang X, Tauchen G. The relative contribution of jumps to total price variance[J]. Journal of Financial Econometrics, 2005, 3(4): 456-499.

[8]Todorov V, Bollerslev T. Jumps and betas: A new framework for disentangling and estimating systematic risks[J]. Journal of Econometrics, 2010, 160(2): 220-235.

[9]Tauchen G, Zhou H. Realized jumps on financial markets and predicting credit spreads[J]. Journal of Econometrics, 2011, 160(1): 102-118.

[10]Guo H, Liu Z, Zhao H, et al. Good jump, bad jump and conditional equity premium[R]. Working Paper, Cincinnati: University of Cincinnati, SSRN ID 2516074, 2014.

[11]陈国进, 王占海. 我国股票市场连续性波动与跳跃性波动实证研究[J]. 系统工程理论与实践, 2010, 30(9): 1554-1562.

Chen Guojin, Wang Zhanhai. Continuous volatility and jump volatility in China’s stock market[J]. Systems Engineering: Theory & Practice, 2010, 30(9): 1554-1562.(in Chinese)

[12]左浩苗, 刘振涛. 跳跃风险度量及其在风险—收益关系检验中的应用[J]. 金融研究, 2011, 376(10): 170-184.

Zuo Haomiao, Liu Zhentao. Jump risk measures and its implication on test of risk-return-trade-off[J]. Journal of Financial Research, 2011, 376(10): 170-184. (in Chinese)

[13]牛华伟. 利率带有跳跃情形下的信用衍生品定价研究[J]. 管理科学学报, 2014, 17(4): 71-85.

Niu Huawei, Pricing credit derivatives with jumps in interest rates[J]. Journal of Management Sciences in China, 2014, 17(4): 71-85. (in Chinese)

[14]赵秀娟， 魏卓， 汪寿阳. 基于日内效应的沪深300股指期货套利分析[J]. 管理科学学报， 2015， 18(1): 73-86.

Zhao Xiujuan, Wei Zhuo, Wang Shouyang. Study on CSI300 index futures’arbitrage based on intraday effect[J]. Journal of Management Sciences in China, 2015, 18(1): 73-86. (in Chinese)

[15]黄冉， 唐齐鸣. 含跳跃风险的公司贷款违约率测算—基于首达时模型的理论扩展[J]. 管理科学学报， 2015， 18(7): 93-102.

Huang Ran, Tang Qiming. Assessing default rate of corporate loan in the first-passage time model with jump risk[J]. Journal of Management Sciences in China, 2015, 18(7): 93-102. (in Chinese)

[16]Reitz T. The equity risk premium: A solution[J]. Journal of Monetary Economics, 1988, 22(1): 117-131.

[17]Barro R. Rare disasters and asset markets in the twentieth century[J]. The Quarterly Journal of Economics, 2006, 121(3): 823-66.

[18]Bollerslev T, Todorov V. Tails, fears, and risk premia[J]. The Journal of Finance, 2011, 66(6): 2165-2211.

[19]Kelly B, Jiang H. Tail risk and asset prices[J]. Review of Financial Studies, 2014, 27(10): 2841-2871.

[20]陈国进, 许秀, 赵向琴. 罕见灾难风险和股市收益—基于我国个股横截面尾部风险的实证分析[J]. 系统工程理论与实践, 2015, 35(9): 2186-2199.

Chen Guojin, Xu Xiu, Zhao Xiangqin. Rare disaster risk and asset return: Evidence from tail risk in Chinese stock market[J]. Systems Engineering: Theory and Practice, 2015, 35(9): 2186-2199. (in Chinese)

[21]Bollerslev T, Law H, Tauchen G. Risk, jumps, and diversification[J]. Journal of Econometrics, 2008, 144(1): 234-256.

[22]Bollerslev T, Todorov V, Li S. Jump tails, extreme dependencies, and the distribution of stock returns[J]. Journal of Econometrics, 2013, 172(2): 307-324.

[23]Chen G, Liu X, Hsieh P. Realized jump risk and equity return in China[J]. Discrete Dynamic in Nature and Society, DOI： 10.1155/2014/721635: 1-13.

[24]Andersen T, Bollerslev T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts[J]. International Economic Review, 1998, 39: 885-905.

[25]Bali T, Peng L. Is there a risk-return tradeoff? Evidence from high-frequency data[J]. Journal of Applied Econometrics, 2006, 21(8): 1169-1198.

[26]Zhang B, Zhao H, Zhu H. Explaining credit default swap spreads with the equity volatility and jump risks of individual firms[J]. Review of Financial Studies, 2009, 22(12): 5099-5131.

[27]Heston S, Rouwenhorst K. Does industrial structure explain the benefits of international diversification?[J]. Journal of Financial Economics, 1994, 36(1): 3-27.

[28]Nijman T, Swinkels L, Verbeek M. Do countries or industries explain momentum in Europe?[J]. Journal of Empirical Finance, 2004, 11(4): 461-481.

[29]Lettau M, Ludvigson S. Measuring and model variation in the risk-return tradeoff[R]. Handbook of Financial Econometrics, Elsevier Science B.V., Amsterdam: North Holland, 2010： 617-690.

[30]Drechsler I, Yaron A. What’s vol got to do with it[J]. Review of Financial Studies, 2011, 24(1): 1-45.

[31]Yan S. Jump risk, stock returns, and slope of implied volatility smile[J]. Journal of Financial Economics, 2010, 99(1): 216-233.

[32]Jiang G, Yao T. Stock price jumps and cross-sectional return predictability[J]. Journal of Financial and Quantitative Analysis, 2013, 48(5): 1519-1544.

[33]郑振龙, 王磊, 王路跖. 特质偏度是否被定价？[J]. 管理科学学报, 2013， 16(5): 1-12.

Zheng Zhenlong, Wang Lei, Wang Lutuo. Is idiosyncratic skewness priced?[J]. Journal of Management Sciences in China, 2013, 16(5): 1-12. (in Chinese)

Realized jump volatility components and portfolio risk premium in Chinese stock market

CHENGuo-jin1, 2,LIUXiao-qun3,XIEPei-lin1, 2,ZHAOXiang-qin2*

1. Wang Yanan Institute for Studies in Economics, Xiamen University, Xiamen 361005， China;2. School of Economics, Xiamen University, Xiamen 361005, China;3. School of Tourism, Hainan University, Haikou 570228, China

Based on the 5-minute high frequency data from the Chinese stock market, and with the non-parametric method, the realized jump volatility components (the size, mean, standard deviation and arrival rate)are estimated, and the empirical results show that: 1) the realized jump volatility components can predict the excessive return of most of the 25 portfolios, with the linear and non-linear time series regression model; 2) the realized jump volatility components have some explanation power for the portfolio return, with the linear cross sectional regression model; 3) the realized jump volatility is possibly the drive force for the size effect and B/M ratio effect in the Fama-French 3-factor model.

portfolio risk premium; realized jump volatility; Fama-French 3-factor model

① 2015-03-26；

2015-12-30.

国家自然科学基金资助项目(71471154; 71571153; 71131008).本文入选“第十二届金融系统工程与风险管理年会”优秀论文(山西大学， 2014年8月).

赵向琴(1966—)， 女， 山西孝义人， 博士， 副教授. Email: xqzhao@xmu.edu.cn