股票收益反转效应及与买卖价差关系研究①

董晨昱, 刘维奇, LIU Wei-min , 王　钰

(1. 山西大学数学科学学院, 太原 030006; 2. 山西大学管理与决策研究中心, 太原 030006;3. 山西大学软件学院, 太原 030006; 4. 山西财经大学财政金融学院, 太原 030006)



股票收益反转效应及与买卖价差关系研究①

董晨昱1, 2, 刘维奇2, 4*, LIU Wei-min2, 王钰3

(1. 山西大学数学科学学院, 太原 030006; 2. 山西大学管理与决策研究中心, 太原 030006;3. 山西大学软件学院, 太原 030006; 4. 山西财经大学财政金融学院, 太原 030006)

研究了买卖价差与股票短期收益反转的关系. 拓展了“真实”价格保持不变或遵循随机游走的假设,在三种情形下对比连续时间上观测价格和“真实”价格的路径图及其价格变化的联合分布来分析买卖价差对股票短期收益反转的影响,结果表明,当“真实”收益的一阶自相关系数接近于0时,买卖价差是造成观测收益反转的唯一原因;当“真实”收益有较强的一阶负自相关性时,买卖价差对观测收益反转的作用不再明显,甚至可能减弱此效应;买卖价差加剧了观测收益的波动.通过买卖价差与股票观测收益间的恒等关系,建立了收益分解模型,将“真实”收益从观测收益中分离,随后使用NASDAQ市场的个股日、周和月数据进行横截面回归和方差比检验,实证结果也支持上述结论.

收益反转; 买卖价差; 方差比检验

0　引　言

股票收益的反转效应是指相邻期股票收益呈负相关的现象.这一现象多年来得到广泛承认,Huang等[1]利用股票月收益的反转效应解释了“特质波动率之谜”,更多学者是将Jegadeesh[2]和Lehmann[3]的短期反转因子作为控制变量用于实证资产定价的研究中,如Bail等[4], Bail等[5],郑振龙等[6].

关于短期收益反转的原因, 一些学者给予了市场微观结构角度的解释.Niederhoffer和Osborne[7]最先指出由于观测价格在买价和卖价间跳跃,从而可能引起股票短期收益的反转. Roll[8]在市场有效且相邻期股票“真实”价格(买卖价差不存在时的价格)保持不变的假设下,建立了有效买卖价差与相邻期股票价格变化协方差间的恒等关系,即表明是买卖价差造成了股票收益的反转.Cohen等[9]使用NYSE和AMEX股票市场数据,通过模拟买卖报价发现短期收益的反转效应是由买卖价差造成的.Jegadeesh和Titman[10]在“真实”价格遵循随机游走的假设下基于存货的市场微观结构模型进一步证实短期收益反转主要由买卖价差引起.Kaul和Nimalendran[11]使用NASDAQ市场的数据,通过方差比检验发现股票日观测收益有较强的负自相关性,而基于收盘卖价计算的日收益表现出较弱的正自相关,从而认为股票日收益反转效应是由于买卖价差造成的.Heston等[12]发现30分钟股票观测收益有滞后多期的负自相关性,基于买价、卖价和买卖报价中点计算的30分钟收益有高于滞后一阶的正自相关系数,而一阶自相关系数仍显著为负,表明买卖价差引起了以30分钟为区间长度的跨期反转效应,但其不能解释相邻期收益的负自相关性. Avramov等[13]认为由于非信息交易者引起的流动性压力需要被流动性提供者补偿,从而产生收益反转,文中刻画流动性采用了Amihud[14]的价格影响流动性指标及四个买卖价差指标,均表明股票周和月收益反转与流动性有很强的关系.Liu[15]以1983年12月至2003年6月NASDAQ市场的所有普通股为样本,发现Amihud的流动性指标与相对买卖价差有很强的线性相关性,两者相关系数为0.941.基于上述文献的分析,股票收益短期反转的市场微观结构解释可归结为是买卖价差的影响.

另有些学者从投资者认知偏差和市场对信息的过度反应等行为角度来解释.Jegadeesh[2]剔除每月最后一个交易日的数据以消除买卖价差的影响,通过横截面回归发现相邻期月股票收益有显著的负相关性,且发现月反转策略有显著溢价,从而认为股票月收益反转效应是由于投资者的行为因素造成的.Lehmann[3]、Daniel等[16]及Barberis等[17]也持相同观点.而Da等[18]不同于上述两种绝对的观点,他们将观测收益减去现金流收益和预期收益所得的剩余收益视作是由投资者情绪及流动性冲击引起的收益,对剩余收益构建月反转策略,其经风险调整的溢价收益是原始反转策略收益的四倍,通过时间序列回归和截面回归发现流动性冲击对多头组合收益有解释作用,投资者情绪对空头组合收益有解释作用,基于此他们得出结论认为月反转策略收益主要归因于投资者情绪和流动性冲击.事实上从文中的分析可知Amihud流动性因子对基于观测收益的反转策略溢价收益有显著的解释力而情绪因子的解释作用不明显.

综上文献分析,基于理论模型研究股票收益反转效应时常限定于市场有效、“真实”价格遵循随机游走等特定假设,如Roll[8]、Jegadeesh和Titman[10]等.通过实证分析解释引起股票短期收益反转的原因时,常基于某一频率数据进行分析,而忽略了不同频率数据的反转效应可能由不同的原因造成这一问题,这也是不同文献得出不同结论的可能原因之一.尽管Avramov等[13]同时考虑了周数据和月数据,两者均是来说明收益反转与流动性有很强的关系:高换手率、低流动性(他们认为交易量和流动性是两个不同的概念)股票表现出更强的负自相关性,且反转策略收益也最大.

本文重新审视这一经典问题,主要基于三点:第1, 考虑到可能存在市场对新到信息的过度反应,以及由于股票供需关系而产生的正常的价格回复,股票的“真实”价格可能围绕其价值上下波动,且基于“真实”价格计算的“真实”收益表现出一定的负自相关性,此时,买卖价差对观测收益反转的影响如何;第2,不同频率的收益反转效应是否由同一因素造成;第3,在实证分析中基于“真实”价格计算的“真实”收益如何获得.

通过实证分析检验买卖价差对股票收益反转效应的影响时,一个重要的问题是如何消除买卖价差对观测收益的影响或者如何获得“真实”收益. Jegadeesh[2]和Lehmann[3]分别采用剔除月末最后一个交易日和一周内周二数据的方法,该时间间隔方法在一定程度上可减弱个股观测收益及组合观测收益中买卖价差的影响,但正如Lehmann[3]指出的,前一天收盘报价为买价或卖价可能会影响第二天收盘时的报价情形(买价或卖价).因此消除一天的数据后,买卖价差的影响仍可能存在,且该方法也丢失了有效数据中所隐含的信息.Blume 和Stambaugh[19]表明由于买卖价差的存在使得股票观测收益与“真实”收益相比有向上的偏差,建议使用买卖报价中点作为股票的“真实”价格,基于报价中点计算的收益作为“真实”收益.Park[20]、Heston等[12]及Han 和 Lesmond[21]也采用了同样的方法.然而,Ho和Stoll[22]证明当做市商的存货不均衡时,报价中点将偏离“真实”价格. Kaul和Nimalendran[11]及Conrad等[23]则基于收盘的卖价计算股票收益以消除买卖价差的影响.此处考虑一种特殊情形:相邻时点上的买卖价差s保持不变,做市商存货均衡,股票的买卖报价中点Pt为其“真实”价格,基于买卖报价中点计算的股票收益为(Pt-Pt-1)/Pt-1,基于卖价Pbt计算的股票收益为:(Pbt-Pbt-1)/Pbt-1,且Pt=Pbt+s/2,显然基于卖价计算的收益高于基于买卖报价中点计算的收益,且基于卖价计算的股票收益也损失了买的指令信息.Daniel 和Titman[24]在研究市场对有形信息和无形信息的反应时,通过建立账面市值比与会计信息收益(有形收益)间的恒等关系从账面市值比中分解出有形收益和无形收益. Donelson和Resutek[25]在研究研发对公司未来收益和盈余预期的影响时借鉴Daniel 和Titman[24]的模型分解思想将公司收益分解为研发收益和非研发收益.这里的模型分解思想为本文从观测收益中分离出“真实”收益提供了借鉴.

本文主要想研究的问题是:在投资者存在认知偏差或对市场新到信息反映过度时,分析买卖价差对股票短期收益反转的影响.本文的主要贡献在于,第1, 拓展了“真实”价格保持不变或遵循随机游走的假设,通过分析三种不同情形连续时间上观测价格和“真实”价格的路径图及其价格变化的联合分布来探究买卖价差与股票短期收益反转效应的关系; 第2,通过不同频率数据的实证比较分析买卖价差对股票收益反转的影响; 第3,通过建立收益分解模型将“真实”收益从观测收益中分离,且该方法可适用于分析买卖价差与各种异象(如“特质波动率之谜”等)的关系.

1　价格变化的自相关性

情形1*Roll[8]仅考虑了此种情形.设短期内股票的“真实”价格等于其价值,且保持不变,买卖价差不随时间变化,记为s,观测价格在买价Pa和卖价Pb间跳跃,且P{Pt=Pa}=P{Pt=Pb}=1/2,各路径均等可能发生.由于“真实”价格保持不变,因此“真实”价格变化的一阶自相关系数为0,下面考虑观测价格变化的一阶自相关系数,图1是t-1时刻观测价格为卖价时的价格路径图.

图1　连续时间区间上观测价格路径图(情形1)

通过上述观测价格路径图可求得在t-1时刻观测价格分别取Pa和Pb的条件下,ΔPt和ΔPt+1的条件联合概率分布列分别为

ΔPtΔPt+10s-s01/401/41/4s1/40

(a)t-1时刻观测价格为卖价

(b)t-1时刻观测价格为买价

(b) Observed price at timet-1 is ask price

图2ΔPt和ΔPt+1的条件联合概率分布列(情形1)

Fig.2 Conditional joint distribution ofΔPtandΔPt+1(Situation 1)

由于假设观测价格分别取Pa和Pb的概率各占1/2,故可得ΔPt和ΔPt+1的无条件联合概率分布列

ΔPt

ΔPt+1-s0s-s01/81/801/81/41/8s1/81/80

图3ΔPt和ΔPt+1的无条件联合概率分布列(情形1)

Fig.3 Unconditional joint distribution ofΔPtandΔPt+1(Situation 1)

进而可求得

Cov(ΔPt,ΔPt+1)=-s2/4

Var(ΔPt)=Var(ΔPt+1)=s2/2

Cor(ΔPt,ΔPt+1)=-1/2

在情形1下,“真实”价格变化的一阶自相关系数为0,而由于买卖价差的存在,使得观测价格变化的一阶自相关系数为-1/2,即“真实”收益序列不相关,观测收益的反转效应是由买卖价差造成的,同时,买卖价差的存在使得观测价格变化产生明显波动.

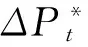
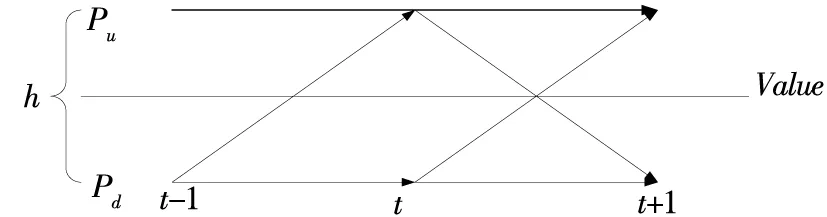
图4　连续时间区间上“真实”价格路径图(情形2)

类似于情形1可求得

考虑到买卖价差的存在,则问题变得复杂的多.为便于计算,取h=2s,各路径均等可能发生,且P{Pt=Pua}=P{Pt=Pub}=P{Pt=Pda}=P{Pt=Pdb}=1/4.图5给出了在t-1时刻,观测价格为Pdb时的价格路径图.在t-1时刻,观测价格分别为Pdb,Pda,Pub,Pua的条件下,观测价格变化的条件联合概率分布列见图6:

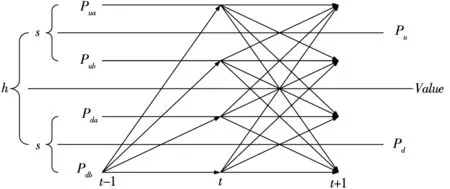
图5　连续时间区间上观测价格路径图(情形2)

ΔPtΔPt+10s2s3s-3s0001/16-2s001/161/16-s01/161/161/1601/161/161/161/16s1/161/161/1602s1/161/16003s1/16000

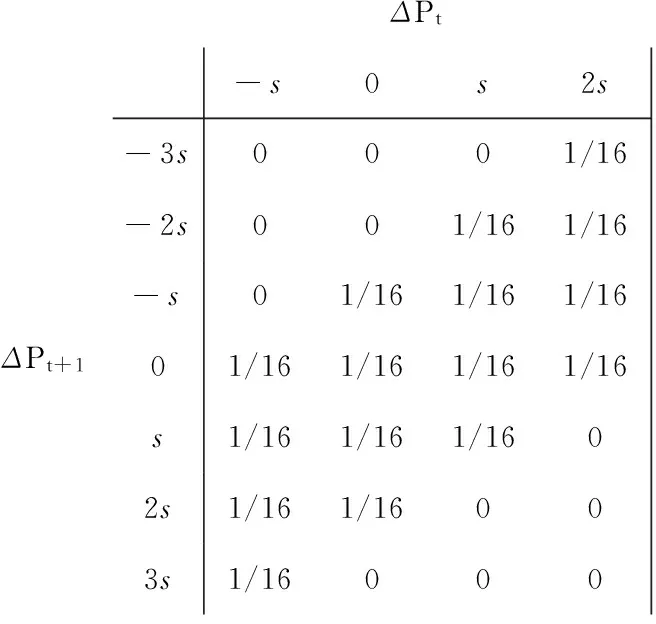
ΔPtΔPt+1-s0s2s-3s0001/16-2s001/161/16-s01/161/161/1601/161/161/161/16s1/161/161/1602s1/161/16003s1/16000

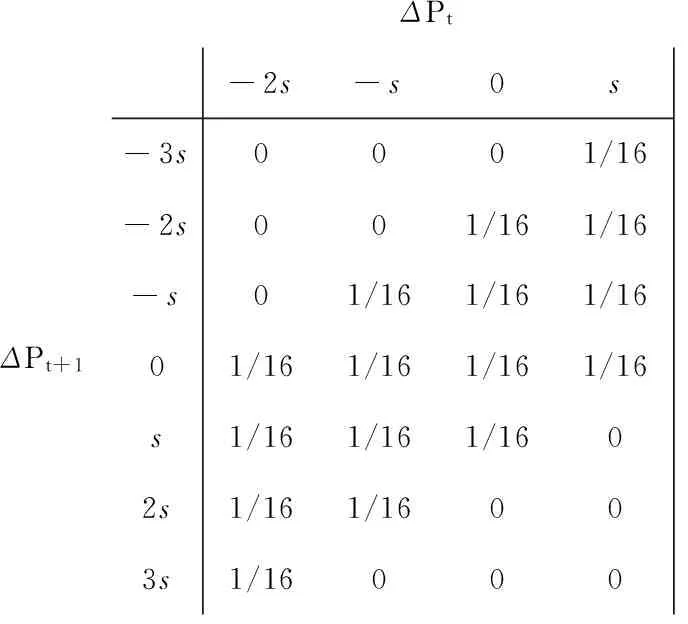
(a)t-1时刻观测价格为Pdb　　　 　　　(b) t-1时刻观测价格为Pda

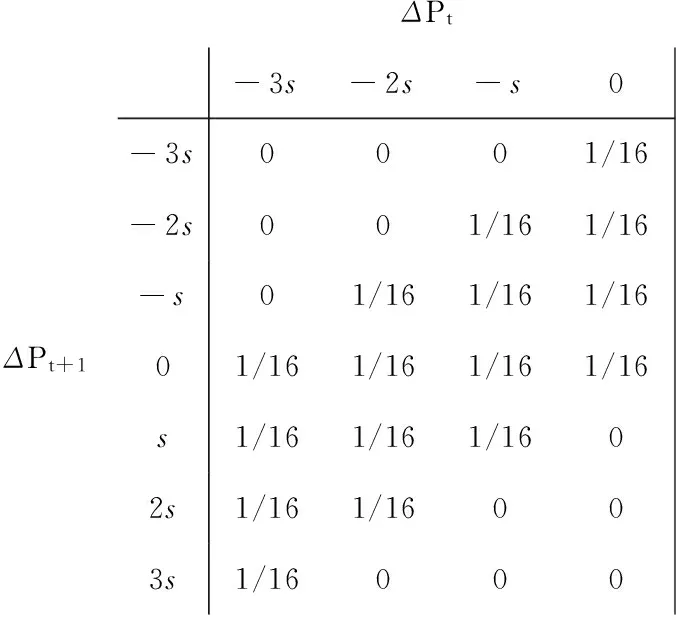
ΔPtΔPt+1-3s-2s-s0-3s0001/16-2s001/161/16-s01/161/161/1601/161/161/161/16s1/161/161/1602s1/161/16003s1/16000

(c)t-1时刻观测价格为Pub(d)t-1时刻观测价格为Pua

图6ΔPt和ΔPt+1的条件联合概率分布列(情形2)

Fig.6 Conditional joint distribution ofΔPtandΔPt+1(Situation 2)

基于上述四个条件联合概率分布列,不难获得相邻期观测价格变化的无条件联合概率分布列:

ΔPtΔPt+1-3s-2s-s0s2s3s-3s0001/161/641/641/64-2s001/162/162/642/641/64-s01/642/163/163/642/641/6401/642/643/164/163/642/641/64s1/642/643/163/642/641/6402s1/642/642/642/641/64003s1/641/641/641/64000

图7ΔPt和ΔPt+1的无条件联合概率分布列(情形2)

Fig. 7 Unconditional joint distribution ofΔPtandΔPt+1(Situation 2)

由ΔPt和ΔPt+1的无条件联合概率分布列可求得

Cov(ΔPt,ΔPt+1)=-5s2/4

Var(ΔPt)=Var(ΔPt+1)=5s2/2=5h2/8>h2/2

Cor(ΔPt,ΔPt+1)=-1/2

在情形2下,“真实”价格变化与观测价格变化有相同的一阶自相关系数-1/2,表明在此种情形下观测收益的反转效应是由投资者对新信息的过度反应等行为因素引起而与买卖价差无关.然而买卖价差的存在使得观测价格变化的波动率要高于“真实”价格变化的波动率.

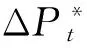
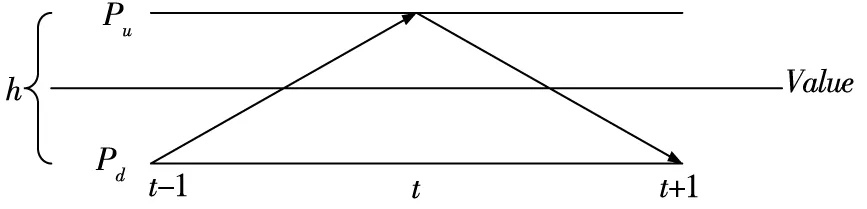
图8　连续时间区间上“真实”价格路径图(情形3)

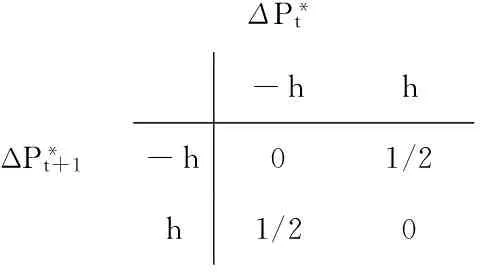
ΔP*tΔP*t+1-hh-h01/2h1/20

从而可求得

在此情形下,图10给出了t-1时刻观测价格为Pdb时的价格路径图,且假设h=2s,各路经均等可能发生,则相邻期观测价格变化的联合分布列如图11.由ΔPt和ΔPt+1的无条件联合概率分布列可求得

Cov(ΔPt,ΔPt+1)=-17s2/4

Var(ΔPt)=Var(ΔPt+1)=9s2/2=9h2/8>h2

Cor(ΔPt,ΔPt+1)=-17/18>-1=

在情形3下,买卖价差的存在削弱了“真实”的价格变化的一阶负自相关关系,但同样增加了价格变化的波动率.

由于股票价格变化与股票收益同方向变化,因此上述三种情形同样适用于分析股票收益的自相关问题.考虑到样本的随机性,买卖价差和“真实”价格波动幅度的时变性,上述三种情形的分析结果表明: 当“真实”收益的一阶自相关系数接近于0时,买卖价差是造成观测收益反转的唯一原因;当“真实”收益有较强的一阶负自相关性时,买卖价差的作用不再明显,甚至可能减弱反转效应;买卖价差的存在使得收益波动率增加.

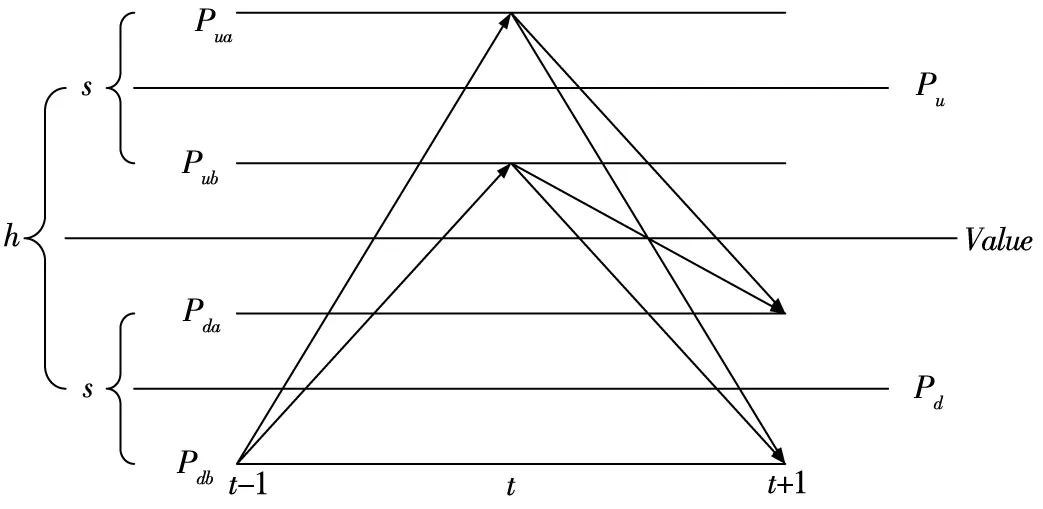
图10连续时间区间上观测价格路径图(情形3)

Fig. 10 Paths of observed price between successive time periods (Situation 3)

ΔPt

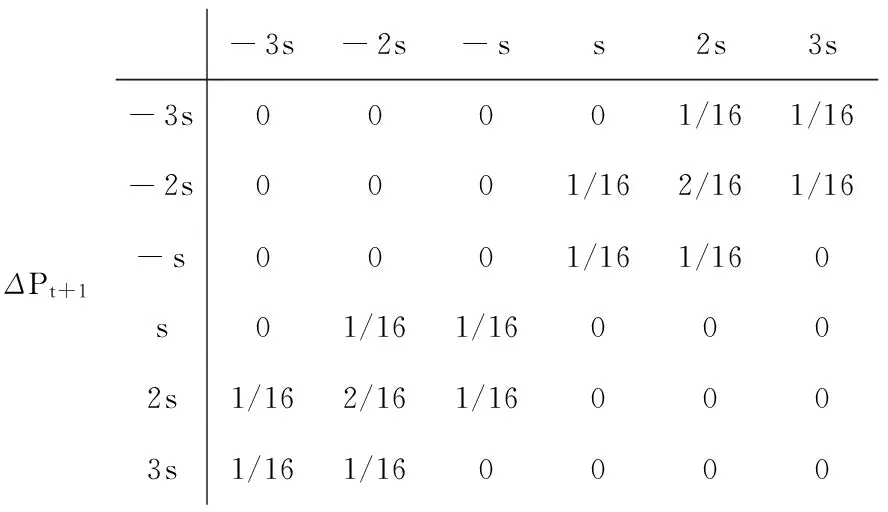
ΔPt+1-3s-2s-ss2s3s-3s00001/161/16-2s0001/162/161/16-s0001/161/160s01/161/160002s1/162/161/160003s1/161/160000

图11ΔPt和ΔPt+1的无条件联合概率分布列(情形3)

Fig. 11 Unconditional joint distribution ofΔPtandΔPt+1(Situation 3)

2　收益分解模型

设t时刻股票的绝对买卖价差为st,即买价pat与卖价pbt的差,pt为t时刻的收盘价*这里的买价、卖价、收盘价均是经价格调整因子调整过的数据.,使用st/pt表示相对买卖价差,且记St=ln(st/pt),文中使用St作为买卖价差的度量指标.不难发现如下恒等关系成立*借鉴了Daniel和Titman[24]的模型设计思想.

(1)

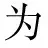
(2)

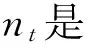
St=St-1+SRt-Rt+nt

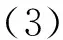
Ri,t=a1Si,t+a2SRi,t+εi,t

3　实证分析

3.1数据描述

考虑到日收盘和月末收盘股票报价的有效性,本文以NASDAQ市场所有普通股(股票代码为10和11的股票)为样本.从CRSP (Center for Research in Security Prices)数据库中选取日末和月末收盘时的交易价、买价、卖价、收益及累积价格调整因子数据.由于NASDAQ市场从1993年1月开始有较完整的买卖报价数据,所以样本从1993-01-01～2012-12-31,共4 660个交易日,240个月.由日数据计算得到相应的周数据,并通过累积价格调整因子调整三种频率(日、周、月)的三类价格(交易价、买价、卖价)数据.

3.2数据基本统计分析

首先基于收益分解模型(4)求每只股票三种频率数据的“真实”收益.日、周和月数据分别以60日、50周和48个月为窗宽*三种频率的样本中分别剔除了不足60日、50周和48个月的股票.,在每个时间区间上对每只股票进行时间序列回归,获得相应的残差序列,即“真实”收益序列.表1给出了三种频率观测收益序列和“真实”收益序列的描述性统计量(首先计算每只股票的特征值,然后以股票为样本求均值).不难发现,三种频率的两类收益序列均有较大的相关性,周收益的相关性最大,达到0.969 6,最小的是月收益,但也达到了0.928 1,从相关性角度来看,买卖价差对月收益反转效应的影响最大.比较两类收益的均值,观测收益均有负的平均收益,而“真实”收益均值接近于零,且偏度也有明显的增加,表明买卖价差的存在降低了股票收益,因此使用买卖价差刻画交易成本是合理的.与均值的结果相反,和观测收益相比“真实”收益的标准差都有所减小, 日数据和周数据的结果更为显著,这与之前的价格变化相关性分析结果一致.直观上时间区间越短,买卖价差对股票收益的影响应该越大,值得注意的是,这种影响更体现在波动率上,而对收益反转效应并非如此.

表1　观测收益和“真实”收益的描述性统计量

3.3横截面回归

分别对三种频率的个股观测收益和“真实”收益建立Jegadeesh[2]的横截面回归模型

其中Rit是股票i在t期的收益,固定时期t,以股票为样本进行上述截面回归,各系数序列在时间上的均值为最终的系数估计.对不同的频率数据选取不同的滞后期,月数据选取J=12,可考察t月的股票收益与滞后一年的各月股票收益的相关性.周数据J=12(最长滞后期为一个季度),日数据J=10(最长滞后期为两周),表2给出了不同频率数据滞后前5期的回归系数及t统计量.

对于三种频率数据,观测收益和“真实”收益均表现出显著的一阶负自相关关系,即存在显著的反转效应.日数据的两个滞后一阶回归系数的绝对值最大,分别为0.129 9和0.137 6,而周数据和月数据滞后一阶回归系数的绝对值均不足日数据的一半,表明日数据的反转效应更为强烈,因此日收益反转策略更有可能获得溢价.

从观测收益的多期滞后回归系数,发现日收益数据表现出高阶的负自相关关系;月收益数据除一阶负自相关外,二阶以上均有显著的正相关关系;而周观测收益数据除存在显著的一阶负自相关关系外,高阶自相关关系不显著,结果表明价格回复周期更接近于一周,月收益数据除反转效应外还有明显的动量效应(t-12月到t-2月的股票收益与t月股票收益正相关).

比较日、周和月“真实”收益的一阶负自相关性,日收益表现最强,月收益最弱,滞后一阶回归系数分别为-0.137 6和-0.050 2,且均显著.分别与其观测收益的滞后一阶回归系数对比,发现消除买卖价差影响后,月收益的反转效应略有减弱,滞后一阶回归系数由-0.053 9上升为-0.050 2,而周收益和日收益的反转效应都有所增强,尤其是日收益数据表现更为明显,滞后一阶回归系数由-0.111 6下降为-0.137 6,表明买卖价差增强了月观测收益的反转效应(即买卖价差和投资者的过度反应共同引起了股票月观测收益的反转效应)而减弱了日和周观测收益的反转效应,即买卖价差的存在提高了股票市场的短期(日和周)效率.这可能是由于短期(日和周)内投资者对新信息的过度反应表现强烈导致股票收益反转,而买卖价差作为交易成本之一能抑制频繁交易的发生,从而削弱了观测收益的反转效应.随着时间延续,投资者对信息的过度反应有所减弱,此时报价的跳跃所引起的收益反转才得以体现.这与前面价格变化相关性分析结果相印证：当“真实”收益的一阶自相关系数接近于0时,买卖价差是造成观测收益反转的唯一原因;当“真实”收益有较强的一阶负自相关性时,买卖价差对观测收益反转效应的作用不再明显,甚至减弱了反转效应.

表2　横截面回归结果

考虑到1997年3月24日和2001年4月9日NASDAQ股票市场最小买卖报价单位分别下降为1/16美元和1/100美元,可能会对研究结果尤其是日数据结果产生影响,同时考虑到2007年波及全球的金融危机,在一定程度上会影响投资者的投资行为,因此,本文考虑了子区间1997-03-24～2001-04-06(子样本Ⅰ)和2001-04-09～2007-11-30(子样本Ⅱ)的日数据横截面分析,结果见表3.

第一个子区间股票市场处于“熊市”阶段,第二个子区间股票市场为“牛市”阶段.在两个阶段,两类日收益均有显著的反转效应.纵向比较,子样本Ⅱ的两类收益回归系数的绝对值均小于对应的子样本Ⅰ的回归系数,表明股票市场行情不佳时,股票日收益表现出更为强烈的负相关关系.横向比较,股票市场不论在“熊市”还是在“牛市”,“真实”收益均比观测收益表现出更强烈的反转效应.因此日收益的反转效应主要由投资者的行为因素主导,在坏的市场行情下表现更为明显.与全样本数据结果类似,买卖价差削弱了股票日收益的负自相关性.

表3　子区间上日收益横截面回归结果

3.4方差比检验

方程比检验是检验某一时间序列是否遵循随机游走的常用方法,这里用来检验两类收益的反转效应.首先构造方差比检验统计量如下

(5)

(6)

这里ρj表示Rt的第j阶自相关系数,j=1,2,…,k-1.即k期方差比近似等于一期收益的前k-1阶自相关系数的加权平均,直观上可以得出结论:1)若股票收益序列不存在自相关关系,则E[VR(k)] =1;2)若股票收益存在反转效应(动量效应),则方差比将小于(大于)1;3)比较两类收益方差比检验统计量的大小,可判断买卖价差在收益反转效应中的作用.根据不同频率的数据,取不同的k值,使用月数据时k=2,4,7,13,周数据取k=2,3,4,5,日数据则取k=2,3,5,6.*不同k的取值，反应所关心的收益序列自相关性的滞后阶数，如在考虑月数据时，取k=2,4,7,13，分别可以考察滞后一个月、一个季度、半年、一年的序列自相关性.

在求方差比检验统计量时,考虑到波动率的时变性,将样本数据进行分割,日、周和月数据分别以60日、50周和48个月为周期,每只股票的方差比检验统计量为各时间段上统计量的均值,而最终三个频率数据的方差比检验统计量是以股票为样本的截面均值, Lo 和MacKinlay[29]证得方差比检验统计量满足渐进正态性,因此在其独立同分布假设下可对其均值是否等于1进行t检验.

表4的第三行和第五行分别是不同数据频率,取不同k值时两类收益的方差比统计量值,第四行和第六行分别是原假设E[VR(k)]=1对备择假设E[VR(k)]<1的检验的t统计量值.从取值可以看出,这里所有的方差比统计量都显著小于1,表明不论是观测收益还是“真实”收益,也不论是日数据、周数据还是月度数据,反转效应均显著存在,且日收益反转效应最为强烈.

比较两类收益的方差比检验结果,发现消除价差影响后,周数据和日数据的两类收益方差比略有减小, 不同于Kaul和Nimalendran[11]的结果：使用日收盘卖价计算收益所得的方差比高于观测收益的方差比,这可能是由于基于卖价计算的日收益波动率低于“真实”收益的波动率所至.月“真实”收益的方差比高于相应观测收益的方差比,当k=2时,“真实”收益的方差比为0.973 7,观测收益的方差比为0.958 7.结果表明买卖价差加剧了股票月观测收益的反转效应,对日收益和周收益的反转效应作用不明显,甚至有所减弱.这里所有结果均与横截面回归分析结果一致,共同印证了价格变化自相关性分析的结果.

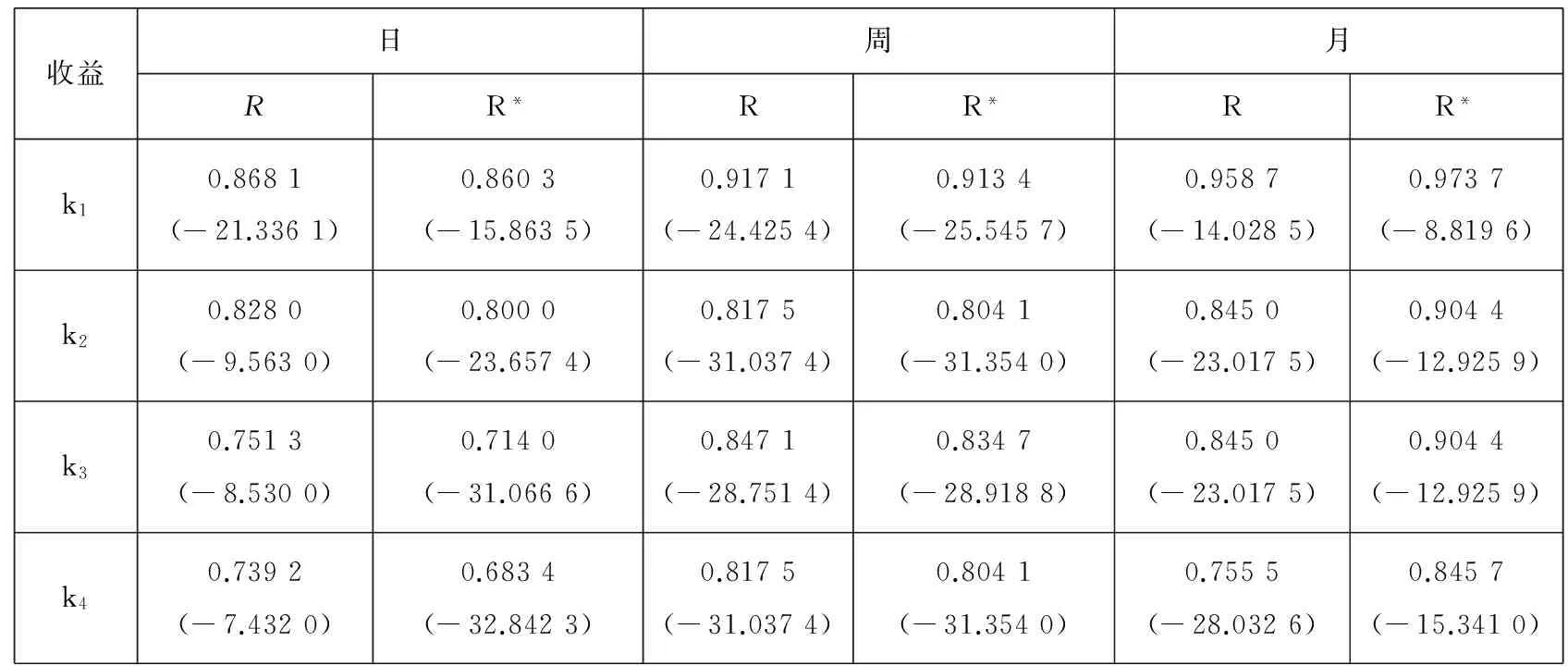
表4　方差比检验结果

4　结束语

通过分析三种情形下连续时间上观测价格和“真实”价格的路径图及其价格变化的联合分布,发现买卖价差的存在加剧了观测收益的波动,但是并不绝对造成股票收益的反转,当股票“真实”收益表现出较强的一阶负自相关性时,买卖价差的作用不再显著.

分别使用日、周、月三种频率数据,通过建立的收益分解模型,将“真实”收益从观测收益中分离,对观测收益和“真实”收益进行横截面回归和方差比检验,发现三种频率数据均存在显著的收益反转效应,日收益的反转效应最强,月收益反转效应最弱,且买卖价差加剧了月收益反转效应,但使得日收益和周收益的反转效应略有减弱,表明买卖价差的存在提高了股票市场的短期(日和周)效率. 需要特别指出的是,直观上时间区间越短,买卖价差对股票收益的影响应该越大,这种影响更体现在波动率上,而对收益反转效应并非如此.

[1]Huang W, Liu Q, Rhee S G, et al. Return reversals, idiosyncratic risk, and expected returns[J]. Review of Financial Studies, 2010, 23(1): 147-168.

[2]Jegadeesh N. Evidence of predictable behavior of security returns[J]. Journal of Finance, 1990, 45(3): 881-898.

[3]Lehmann B N. Fads, martingales, and market efficiency[J]. Quarterly Journal of Economics, 1990, 105(1): 1-28.

[4]Bali T G, Cakici N, Whitelaw R F. Maxing out: Stocks as lotteries and the cross-section of expected returns[J]. Journal of Financial Economics, 2011, 99(2): 427-446.

[5]Bali T G, Peng L, Shen Y, et al. Liquidity shocks and stock market reactions[J]. Review of Financial Studies, 2014, 27(5): 1434-1485.

[6]郑振龙, 王磊, 王璐拓. 特质偏度是否被定价？[J]. 管理科学学报, 2013, 16(5): 1-12.

Zheng Zhenlong, Wang Lei, Wang Lutuo. Idiosyncratic skewness is pricing?[J]. Journal of Management Sciences in China, 2013, 16(5): 1-12.(in Chinese)

[7]Niederhoffer V, Osborne M F M. Market making and reversal on the stock exchange[J]. Journal of American Statistical Association, 1966, 61(316): 897-916.

[8] Roll R. A simple implicit measure of the effective bid-ask spread in an efficient market[J]. Journal of Finance, 1984, 39(4): 1127-1139.

[9] Cohen K J, Maier S F, Schwartz R A, et al. On the existence of serial correlation in an efficient securities market[M]// Portfolio Theory, Portfolio Theory, 25 Years After: Essays in Honor of Harry Markowitz. New York: Elsevier North-Holland, 1979: 151-168.

[10]Jegadeesh N, Titman S. Short-horizon return reversals and the bid-ask spread[J]. Journal of Financial Intermediation, 1995, 4(2): 116-132.

[11]Kaul G, Nimalendran M. Price reversals: Bid-ask errors or market overreaction?[J]. Journal of Financial Economics, 1990, 28(1-2): 67-83.

[12]Heston S L, Korajczyk R A, Sadka R. Intraday patterns in the cross-section of stock returns[J]. Journal of Finance, 2010, 65(4): 1369-1407.

[13]Avramov D, Chordia T, Goyal A. Liquidity and autocorrelations in individual stock returns[J]. Journal of Finance, 2006, 61(5): 2365-2394.

[14]Amihud Y. Illiquidity and stock returns: Cross-section and time-series effects[J]. Journal of Financial Markets, 2002, 5(1): 31-56.

[15]Liu W. A liquidity-augmented capital asset pricing model[J]. Journal of Financial Economics, 2006, 82(3): 631-671.

[16]Daniel K, Hirshleifer D, Subrahmanyam A. Investor psychology and security market under-and over-reactions[J]. Journal of Finance, 1998, 53(6): 1839-1886.

[17]Barberis N, Shieifer A, Vishny R. A model of investor sentiment[J]. Journal of Financial Economics, 1998, 49(3): 307-343.

[18]Da Z, Liu Q, Schaumburg E. A closer look at the short-term return reversal[J]. Management Science, 2014, 60(3): 658-674.

[19]Blume M, Stambaugh R F. Biases in computed returns: An application to the size effect[J]. Journal of Financial Economics, 1983, 12(3): 387-404.

[20]Park J. A market microstructure explanation for predictable variations in stock returns following large price changes[J]. Journal of Financial and Quantitative Analysis, 1995, 30(2): 241-256.

[21]Han Y, Lesmond D. Liquidity biases and the pricing of cross-sectional idiosyncratic volatility[J]. Review of Financial Studies, 2011, 24(5): 1590-1629.

[22]Ho T, Stoll H. On dealer markets under competition[J]. Journal of Finance, 1980, 35(2): 259-267.

[23]Conrad J, Gultekin M N, Kaul G. Profitability of short-term contrarian strategies: Implications for market efficiency[J]. Journal of Business & Economic Statistics, 1997, 15(3): 379-386.

[24]Daniel K, Titman S. Market reactions to tangible and intangible information[J]. Journal of Finance, 2006, 61(4): 1605-1643.

[25]Donelson D C, Resutek R J. The effect of R&D on future returns and earnings forecasts[J]. Review Account Study, 2012, 17(4): 848-876.

[26]孔东民, 孔高文, 刘莎莎. 机构投资者、 流动性与信息效率[J]. 管理科学学报, 2015, 18(3): 1-15.

Kong Dongmin, Kong Gaowen, Liu Shasha. Institutional investors, liquidity and information efficiency[J]. Journal of Management Sciences in China, 2015, 18(3): 1-15. (in Chinese)

[27]文凤华, 肖金利, 黄创霞， 等. 投资者情绪特征对股票价格行为的影响研究[J]. 管理科学学报, 2014, 17(3): 60-69.

Wen Fenghua, Xiao Jinli, Huang Chuangxia, et al. The influence research of investor sentiment on stock price behavior[J]. Journal of Management Sciences in China, 2014, 17(3): 60-69. (in Chinese)

[28]Cochrane J H. How big is the random walk in GNP?[J]. Journal of Political Economy, 1988, 96(5): 893-920.

[29]Lo A W, MacKinlay A C. Stock market prices do not follow random walks: Evidence from a simple specification test[J]. Review of Financial Studies, 1988, 1(1): 41-66.

Research on reversal effect and the relationship between reversal effect and bid-ask spread

DONGChen-yu1, 2,LIUWei-qi2, 4*,LIUWei-min2,WANGYu3

1. School of Mathematical Sciences, Shanxi University, Taiyuan 030006, China;2. Research Center for Management and Decision Making, Shanxi University, Taiyuan 030006, China;3. School of Software Engineering, Shanxi University, Taiyuan 030006, China;4. Faculty of Finance and Banking, Shanxi University of Finance and Economics, Taiyuan 030006, China

The paper analyzes the relationship between the bid-ask spread and stock short-run return reversals in individual stocks. This paper extends the assumption that the “true” price remains constant or follows random walk. Contrasted paths of observed price and “true” price between successive time periods, and adjacent period joint distribution of observed price change and the “true” price change in three cases, we analyze the impact of the bid-ask bounce on the return reversal. The results show, the bid-ask spread is the only reason for stock observed return reversal when the first order autocorrelation coefficient of the stock “true” return is close to 0; the role of the bid-ask spread on observed return reverse is not obvious and may even weaken the reverse when the “true” return has a strong negative first order autocorrelation; the bid-ask spread intensify the volatility of observed return. Based on the identity relation between bid-ask spread and stock return, we establish the return decomposition model to isolate the “true” return from the observed return, and cross section regression and variance-ratio test are adopted to support these conclusions using individual stocks daily, weekly and monthly data in NASDAQ market respectively.

return reverse; bid-ask spread; variance-ratio test

① 2015-03-26；

2015-12-26.

国家自然科学基金资助项目(71371113); 教育部人文社科基金资助项目(13YJA790154).本文入选“第十二届金融系统工程与风险管理年会”优秀论文(山西大学， 2014年8月).

刘维奇(1963—), 男, 山西忻州人, 博士, 教授, 博士生导师. Email: liuwq@sxu.edu.cn

F830

A

1007-9807(2016)06-0171-12