广义近似保等分线正交映射

孔　亮,王念良,刘晓民

(商洛学院 数学与计算机应用学院 应用数学研究所,陕西 商洛　726000)



广义近似保等分线正交映射

孔亮,王念良,刘晓民

(商洛学院 数学与计算机应用学院 应用数学研究所,陕西 商洛726000)

在实赋范线性空间中,给出了广义近似等分线正交的定义和性质以及广义近似保等分线正交映射的定义。运用算子论方法,证明了(δ1,δ2)-近似等距是广义近似保等分线正交映射,得到了有界线性映射成为广义近似保等分线正交映射的一些充分条件。

近似等距;等分线正交;近似等分线正交;广义近似保等分线正交映射

正交性是内积空间的重要概念。自20世纪初,许多学者相继在赋范线性空间中推广了内积空间中的正交性,得到了各种正交性定义,如R-正交、B-正交、I-正交、P-正交等[1-8],至今新的正交性定义被不断引入和研究。为了更深入地研究赋范线性空间的几何性质,一些学者在内积空间、准HilbertA-模、赋范线性空间中引入各种近似正交性定义并研究其性质[9-12]。同时保持和近似保持各种正交性映射的性质,受到了众多学者的关注。文献[9,10]中在内积空间中给出了线性保正交映射的刻画;文献[11]中在Hilbert空间中证明了非零近似保正交线性映射有界并且是下有界的;文献[12]中在准HilbertA-模中推广了文献[11]中的结果;文献[13]中在实赋范线性空间中给出了近似保等分线正交映射的定义和性质;关于其他各种近似保正交映射已有许多研究[14-22]。受文献[1-22]中概念和结论的启发,研究在实赋范线性空间中引入广义近似保等分线正交映射的定义,研究有界线性映射成为广义近似保等分线正交映射的一些充分条件。

1　预备知识

在研究中,X和Y表示实赋范线性空间,H表示实Banach空间,表示实数域。

定义1设δ∈[0,1),U∶X→Y是线性映射。若U满足

(1-δ)‖x‖≤‖U(x)‖≤(1+δ)‖x‖,∀x∈X

则称U是δ-近似等距[14]。

定义2设δ1,δ2∈[0,1),U∶X→Y是线性映射。若U满足

(1-δ1)‖x‖≤‖U(x)‖≤(1+δ2)‖x‖,∀x∈X

则称U是(δ1,δ2)-近似等距。

定义4设x,y∈X,δ∈[0,1)。若

定义5设x,y∈X,δ1,δ2∈[0,1)。若

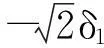
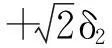
命题1设x,y∈X,δ1,δ2∈[0,1),α,β∈,则:

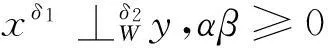
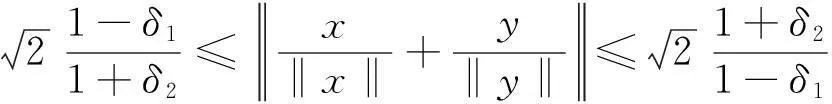
(1)

若x和y线性相关,则存在s≠0使y=sx,从而由式(1)知

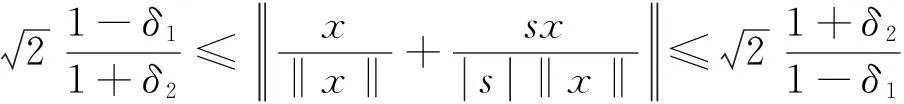
(2)

定义6设映射T∶X→Y,δ,ε∈[0,1)。若对任意的x,y∈X,xδ⊥Wy⟹T(x)ε⊥WT(y),则称T是近似保等分线正交映射[13]。

注2在定义7中,当δ1=δ2=δ,ε1=ε2=ε时,T是近似保等分线正交映射,从而定义7是定义6的一个推广。

2　主要结果及其证明

引理1设x,y∈X{0},则[15]

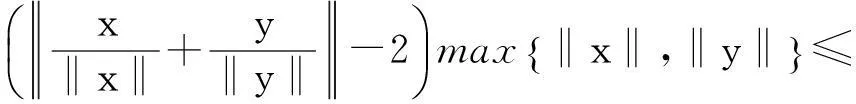
(1-δ1)‖z‖≤‖U(z)‖≤(1+δ2)‖z‖,∀z∈X

(3)

于是

(1-δ1)‖x‖≤‖U(x)‖≤(1+δ2)‖x‖, (1-δ1)‖y‖≤‖U(y)‖≤(1+δ2)‖y‖

和

(4)

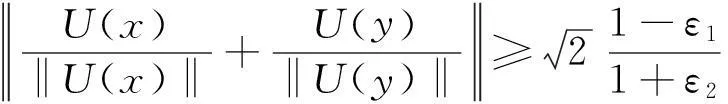
(5)

则T是广义近似保等分线正交映射。

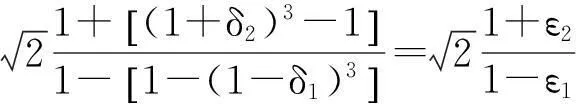
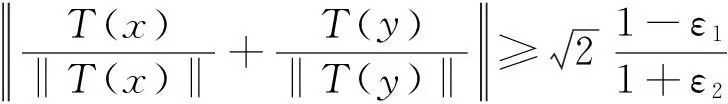
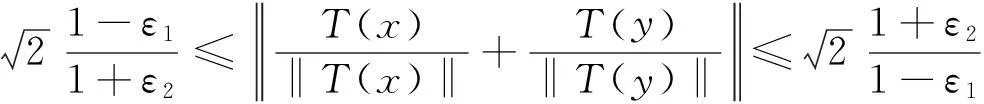
引理2设δ1,δ2∈[0,1)。若线性映射T∶H→H满足

‖T(x)-x‖≤δ1‖x‖+δ2‖T(x)‖,∀x∈H

则T是有界满射,且

‖T(x)-x‖≤δ1‖x‖+δ2‖T(x)‖,∀x∈H

则T和T-1都是广义近似保等分线正交映射。

证明由引理2得

(6)

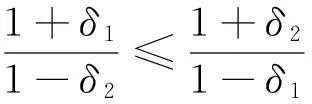
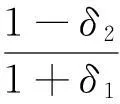
(7)

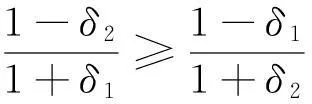
[1]Roberts B D.On the Geometry of Abstract Vector Space[J].Thoku Math J,1934,39:42-59.

[2]Birkhoff G.Orthogonality in Linear Metric Space[J].Duck Math J,1935,1(2):169-172.

[3]James R C.Orthogonality in Normed Linear Space[J].Duck Math J,1945,12(2):291-302.

[4]Diminnie C R.A New Orthogonality Relation for Normed Linear Spaces[J].Math Nachr,1983,114(1):197-203.

[5]Alonso J,Soriano M L.On Height Orthogonality in Normed Linear Spaces[J].Rocky Mt J Math,1999,29(4):1 167-1 183.

[6]Saidi F B.An Extension of the Notion of Orthogonality to Banach Spaces[J].J Math Anal Appl,2002,267(1):29-47.

[7]Chmieliński J,Wójcik P.On a ρ-orthogonality[J].Aequationes Math,2010,80(1):45-55.

[8]Alonso J,Martini H,Wu S.On Birkhoff Orthogonality and Isosceles Orthogonality in Normed Linear Spaces[J].Aequationes Math,2012,83(1/2):153-189.

[9]Chmieliński J.Linear Mappings Approximately Preserving Orthogonality[J].J Math Anal Appl,2005,301(1):158-169.

[10]Chmieliński J.Stability of the Orthogonality Preserving Property in Finite-dimensional Inner Product Spaces[J].J Math Anal Appl,2006,318(2):433-443.

[11]Turnšek A.On Mappings Approximately Preserving Orthogonality[J].J Math Anal Appl,2007,336(1):625-631.

[13]Zamani A.Approximately Bisectrix-orthogonality Preserving Mappings[J].Commentationes Mathematicae,2014,54(2):167-176.

[14]Ding G G.The Approximation Problem of Almost Isometric Operators by Isometric Operators[J].Acta Math Sci,1988,8(4):361-372.

[15]Maligranda L.Simple Norm Inequalities[J].Amer Math Monthly,2006,113(3):256-260.

[16]Cazassa P G,Christensen O.Perturbation of Operators and Applications to Frame Theory[J].J Fourier Anal Appl,1997,3(5):543-557.

[17]Chmieliński J,Wójcik P.Isosceles-orthogonality Preserving Property and Its Stability[J].Nonlinear Anal,2010,72(8):1 445-1 453.

[18]孔亮,曹怀信.ε-近似保正交映射的稳定性与扰动[J].数学学报,2010,53(1):61-66.

[19]Mojškerc B,Turnšek A.Mapping Approximately Preserving Orthogonality in Normed Spaces[J].Nonlinear Anal,2010,73(12):3 821-3 831.

[20]Wójcik P.Linear Mappings Preservingρ-orthogonality[J].J Math Anal Appl,2012,386(1):171-176.

[21]孔亮,李超.Hilbert空间上的(δ,ε)-近似保正交映射[J].甘肃科学学报,2014,26(4):1-4.

[22]孔亮,曹怀信.ε-近似保平方等腰正交映射的刻画与扰动[J].山东大学学报:理学版,2015,50(6):75-82.

Generalized Approximate Preserving Bisectrix Orthogonal Mapping

Kong Liang,Wang Nianliang,Liu Xiaomin

(College of Mathematics and Computer Application,Institute of Applied Mathematics,Shangluo University,Shangluo 726000,China)

In real normal linear space,it gives the definition and property of the generalized approximate bisectrix orthogonality,and also gives the definition of approximate preserving bisectrix orthogonal mapping,and uses the theory of operator to show (δ1,δ2) approximate equidistance is the generalized approximate preserving bisectrix orthogonal map,knowing that the bounded linear mapping is the sufficient condition of generalized approximate preserving bisectrix orthogonal mapping.

Approximate equidistance;Bisectrix orthogonality;Approximate bisectrix orthogonality;Generalized approximate preserving bisectrix orthogonal mapping

10.16468/j.cnki.issn1004-0366.2016.04.004.

2015-09-23;

2015-10-26.

陕西省科技厅科研项目(2014JM1019);陕西省教育厅科研项目(15JK1221);商洛学院博士团队服务地方科技创新与经济社会发展能力提升专项子项目(SK2014-01-08);商洛学院科研项目(14SKY016).

孔亮(1983-),男,陕西商洛人,硕士,讲师,研究方向为泛函分析.E-mail:kongliang2005@163.com.

O177.1

A

1004-0366(2016)04-0013-05

引用格式:Kong Liang,Wang Nianliang,Liu Xiaomin.Generalized Approximate Preserving Bisectrix Orthogonal Mapping[J].Journal of Gansu Sciences,2016,28(4):13-16,22.[孔亮,王念良,刘晓民.广义近似保等分线正交映射[J].甘肃科学学报,2016,28(4):13-16,22.]