冲击速度对带支撑钢构格栅坝抗冲击性能的影响

刘旭东,胡志明

(1.兰州理工大学 土木工程学院,甘肃 兰州　730050；2.甘肃建筑职业技术学院,甘肃 兰州　730050)



冲击速度对带支撑钢构格栅坝抗冲击性能的影响

刘旭东1,胡志明2

(1.兰州理工大学 土木工程学院,甘肃 兰州730050；2.甘肃建筑职业技术学院,甘肃 兰州730050)

带支撑钢构格栅坝在拦截大石块,减小泥石流冲击破坏中有十分重要的作用。利用非线性有限元软件ANSYS/LS-DYNA对带支撑钢构格栅坝结构模型进行数值模拟。用钢球模拟巨石,以不同的冲击速度在格栅坝中间榀顶层梁柱节点施加冲击荷载,分析在冲击荷载作用下结构的动力响应。结果表明:带支撑钢构格栅坝各处位移随着钢球冲击速度的增加逐渐增大,基本呈现线性变化的规律,尤其在冲击作用点处结构的位移变化率最大,且距冲击作用位置越远位移变化率越小；结构各处应力值随着冲击速度的增加而增大,且距冲击作用位置较远的单元应力变化接近线性增长规律；随着冲击速度的提升,结构各柱脚支反力逐渐增大。

带支撑钢构格栅坝;冲击速度;抗冲击性能;LS-DYNA;数值模拟

钢构格栅坝拦截泥石流中的巨石以防止其对建筑物造成灾难性的冲击破坏,在泥石流防治领域起到了举足轻重的作用[1,2]。然而,面对诸如甘肃舟曲“8.8”特大泥石流灾害,钢构格栅坝在7.5 m直径的巨石以将近10 m/s的速度冲击下就会略显脆弱[3]。因此,为了更加有效地抵抗泥石流中巨石的冲击作用,确保钢构泥石流格栅坝在泥石流发生过程中不被破坏,仍能继续发挥拦截巨石的作用,研究提出了带支撑钢构格栅坝这一新型结构[4,5],利用非线性有限元软件ANSYS/LS-DYNA进行数值模拟,用钢球模拟巨石,分别以2 m/s、 4 m/s、 6 m/s、 8 m/s、 10 m/s这五组不同速度作用于钢构格栅坝中间榀顶层梁柱节点,通过对比分析不同速度冲击作用下带支撑钢构格栅坝的响应,提取出了结构位移、应力、支反力以及加速度随冲击速度的变化规律[6],为工程应用提供参考。

1　冲击速度的确定

低速泥石流流速一般为2～10 m/s,研究将冲击速度划分为2 m/s、4 m/s、6 m/s、8 m/s、10 m/s五档,利用非线性有限元软件LS-DYNA进行数值模拟,分别模拟各速度巨石冲击作用下带支撑钢构格栅坝的动态响应[7,8]。

2　有限元模型的建立

2.1钢球有限元模型

采用直径为0.3 m的钢球模拟泥石流冲击过程中的巨石,在有限元软件ANSYS/LS-DYNA中建立钢球模型。钢球选取ANSYS/LS-DYNA中提供的刚体单元SOLID168单元,其本构关系采用刚体模型。钢球网格尺寸取0.02 m,其有限元模型网格划分如图1所示。

将钢球作用于格栅坝中间榀顶层梁柱节点作为一种冲击作用工况。

2.2带支撑钢构格栅坝有限元模型

带支撑钢构格栅坝有限元模型建立过程中选用4节点空间薄壳单元SHELL163单元,单元厚度8 mm,剪切因子取5/6,采用程序默认的Belytschko(def)算法；本模型材料屈服强度235 MPa,弹性模量205 GPa,泊松比0.3,密度7.85×103kg/m3,本构关系采用双线性各向同性模型,材料的屈服遵循Von Mises屈服准则；钢格栅坝由五榀钢架通过横梁及水平梁相连,各榀间距0.5 m,每榀钢架为两跨两层,跨度均为0.5 m,第一层高度0.61 m,第二层高度0.4 m。模型中钢构件均采用H100X100X8X8工字型钢,网格划分尺寸为20 mm；本模型选择ANSYS/LS-DY-NA程序提供的单面自动接触算法(ASTS,automaticsurface to surface)。结构有限元模型如图2所示。本次模拟由于2 m/s的钢球速度较小,需要的计算时间增加到0.05 s。

图1　钢球有限元模型Fig.1　Finite element model of steel ball

图2　带支撑钢构格栅坝有限元模型Fig.2　Finite element model of steel grilled dam with support

3　有限元结果对比分析

3.1结构位移对比分析

由于该结构模型属于对称结构,故按图3对钢构格栅坝的一半进行取点并提取不同冲击速度下各点位移值,见表1。

通过对表1的分析可知,结构在5点处,由于其为固定端,故结构在该处的位移为0；结构在各冲击速度下位移最大值均发生在冲击作用点处,且冲击速度越大结构的位移越大；结构在冲击作用点处位移随速度的变化率最大,离冲击作用点越远位移随速度的变化率越小。表1中各位移数据随速度的变化规律见图4。

图3　测点布置Fig.3　Layout of measurement points

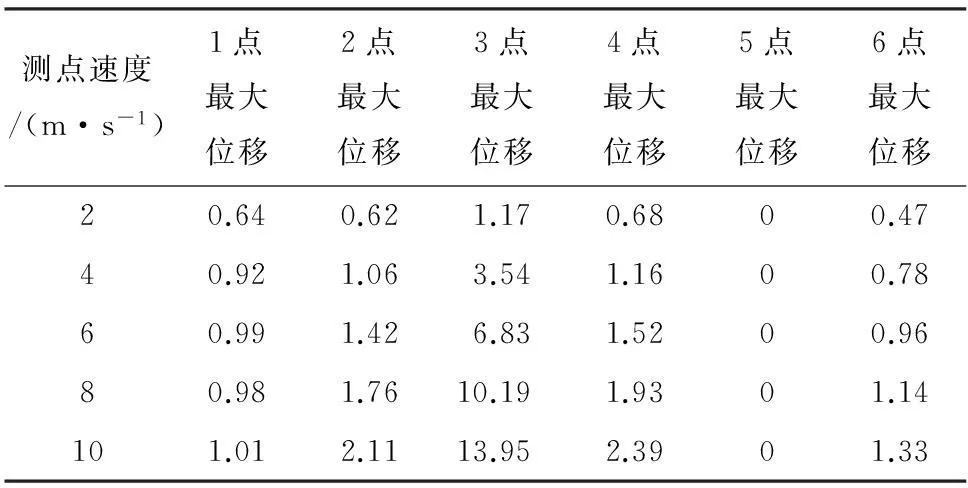
测点速度/(m·s-1)1点最大位移2点最大位移3点最大位移4点最大位移5点最大位移6点最大位移20.640.621.170.6800.4740.921.063.541.1600.7860.991.426.831.5200.9680.981.7610.191.9301.14101.012.1113.952.3901.33

图4　不同速度下位移变化Fig.4　Displacement changes under different speeds

由图4可以清楚地看到,结构各点的位移值随着钢球冲击速度的增加逐渐增大,基本上呈现出线性变化的规律,尤其在冲击作用点处(3号点)结构的位移变化率最大,结构其他点距冲击作用点位置越远变化率越小,其中5号点处于结构的嵌固端,位移值保持零值不变；同一冲击速度作用下,结构在被冲击部位位移最大,离冲击位置越远位移值越小。

3.2Von Mises应力对比分析

带支撑钢构格栅坝在各冲击速度下的应力云图如图5～图9所示,由于对称性仍提取一半结构进行分析。

由图5～图9可以看出:2 m/s冲击速度下结构整体响应很小,只在冲击作用部位应力较大,4 m/s冲击速度下结构被冲击榀应力较大,其他各榀响应较小,当冲击速度达到6 m/s时,结构的应力大幅增大,相邻榀钢架的响应随之增加,尤其当速度达到10 m/s时,结构各构件均不同程度的达到屈服强度。现按图3的测点布置提取各点的应力值,见表2。

图5　2 m/s下带支撑钢构格栅坝Von Mises应力云图Fig.5　Von Mises stress cloud chart of steel grilled dam with support in 2 m/s

图6　4 m/s下带支撑钢构格栅坝Von Mises应力云图Fig.6　Von Mises stress cloud chart of steel grilled dam with support in 4 m/s

图7　6 m/s下带支撑钢构格栅坝Von Mises应力云图Fig.7　Von Mises stress cloud chart of steel grilled dam with support in 6 m/s

图8　8 m/s下带支撑钢构格栅坝Von Mises应力云图Fig.8　Von Mises stress cloud chart of steel grilled dam with support in 8 m/s

图9　10 m/s下带支撑钢构格栅坝Von Mises应力云图Fig.9　Von Mises stress cloud chart of steel grilled dam with support in 10 m/s

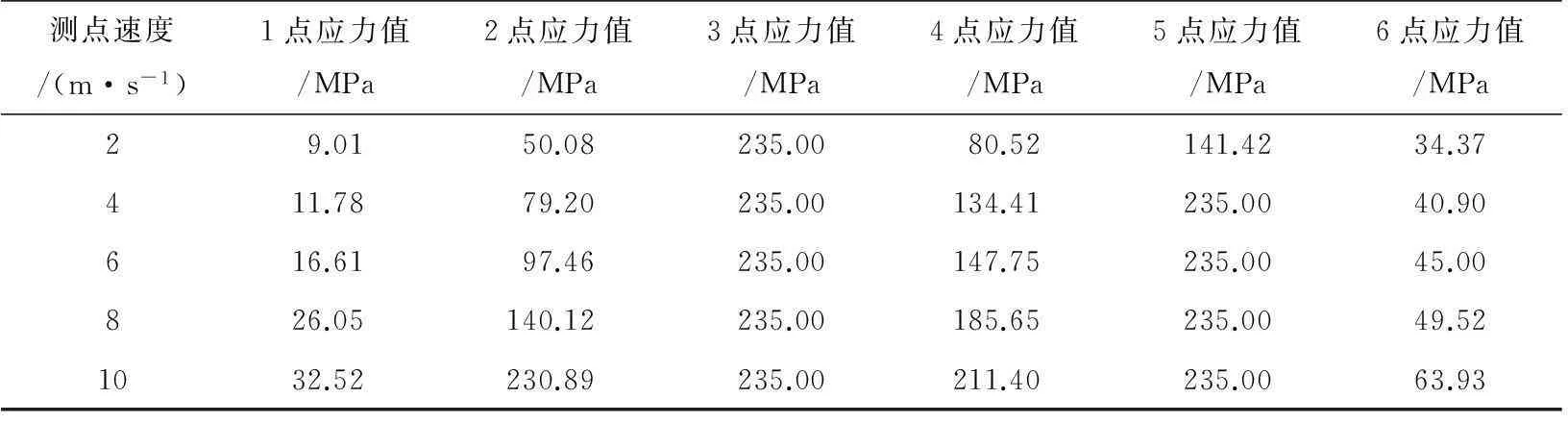
表2　各点应力值

表2各应力数据随速度的变化规律如图10所示。

由图10及表2可知,结构在冲击作用部位(3号点)应力最大,达到屈服强度,结构支座位置(5号点)在2 m/s速度作用下应力为141.42 MPa,随着速度的进一步增大,该处的应力值也达到屈服强度；由1、2、4、6号点知,冲击速度一定时,结构距冲击作用位置越近构件应力值越大；各点应力值随着冲击速度的增加而增大,且距冲击作用位置较远的点位应力变化近乎线性规律,如1号及6号点,而其他点处的应力变化虽有所增大,但并无明显规律可循。

3.3支反力对比分析

提取冲击作用方向,即Y向的最大支反力FYmax(剪力,kN)进行分析。按图11中柱脚编号提取各柱脚支反力值,见表3。

图10　不同速度下应力变化Fig.10　Stress changes under different speeds

图11　柱脚编号示意图Fig.11　Number diagram of pillar

速度/(m·s-1)1点支反力/kN2点支反力/kN3点支反力/kN4点支反力/kN5点支反力/kN6点支反力/kN7点支反力/kN8点支反力/kN9点支反力/kN280.8932.9880.5061.3223.8460.6557.1819.3454.954121.9151.47126.5595.9537.7797.8081.9930.1481.076131.8757.26132.32110.2343.81113.8877.5929.5878.648140.9271.18134.60123.1047.51125.6983.3329.3685.4410143.1081.36138.21131.7952.19131.8882.1530.9186.42

表3各柱脚支反力数据随速度的变化规律如图12所示。

由表3及图12可知,随着冲击速度的提升,结构各柱脚支反力逐渐增大,且冲击速度由2 m/s增加到4 m/s时结构的支反力增长率最大,其后随着速度的加大,支反力增大的斜率逐渐减小；同时,冲击速度不变的情况下,由图12可以直观看出结构在2、5、8三处柱脚的支反力小于结构其他部位的反力值,1、3号柱脚的支反力最大,且结构在1、3号柱脚的支反力相当接近,同样4、6号,7、9号柱脚支反力亦很接近。

3.4加速度对比分析

提取Y向加速度值进行分析对比。按图3所示各测点提取其加速度峰值进行对比分析,加速度峰值数据见表4。

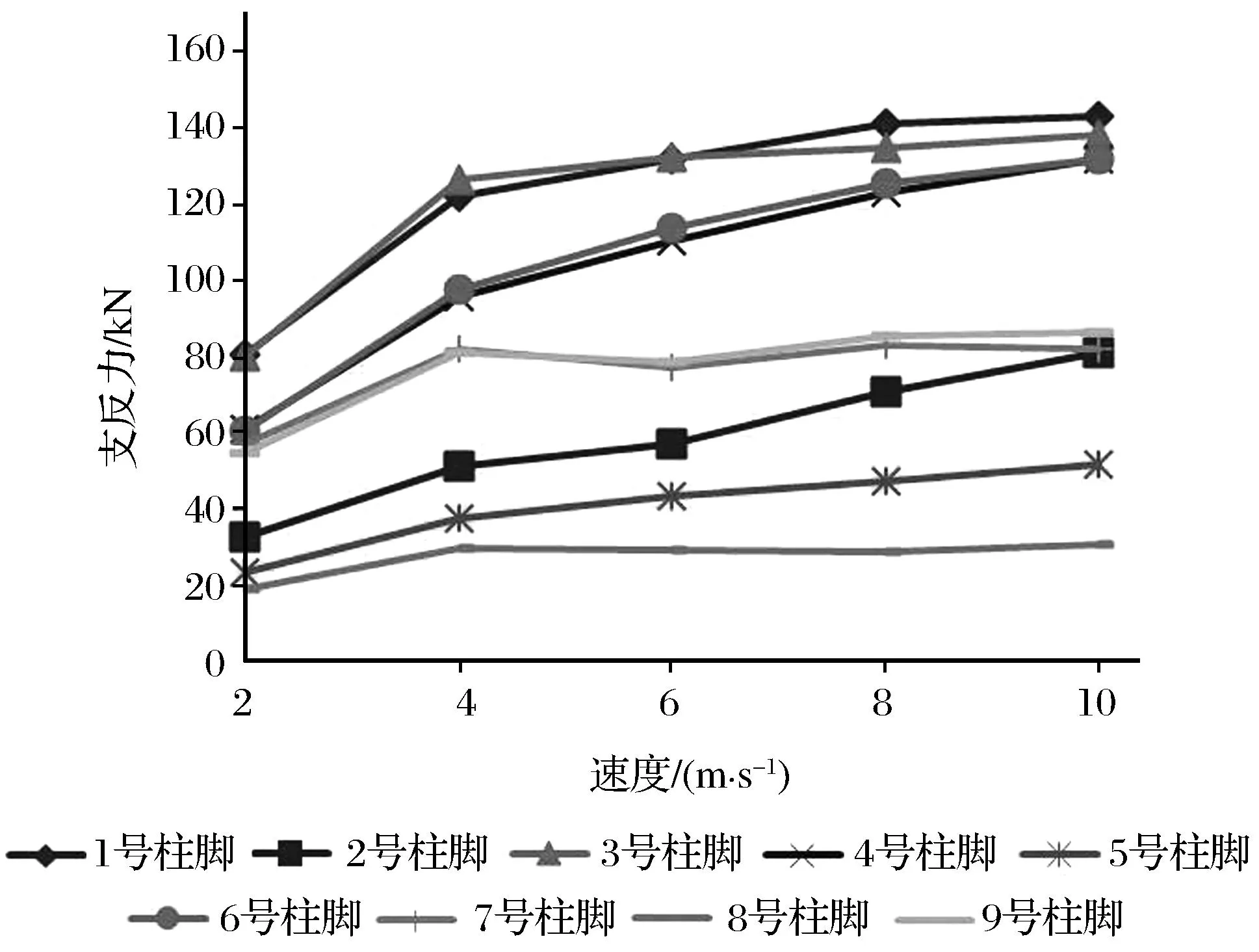
图12　不同速度下支反力变化Fig.12　Bearing reaction changes at different speeds

测点速度/(m·s-1)1点最大加速度/(m·s-2)2点最大加速度/(m·s-2)3点最大加速度/(m·s-2)4点最大加速度/(m·s-2)5点最大加速度/(m·s-2)6点最大加速度/(m·s-2)217241687482724440160743390298243183242017696287440105400727150240682580252461411291702497102721297321829529602729

由表4可知,5点位于结构嵌固端,加速度值为0,结构加速度最大值出现在冲击作用部位,即3点处；对表4中各测点不同冲击速度下的加速度峰值进行对比可知,加速度随冲击速度的变化规律并不明显。

4　结论

通过对带支撑钢构格栅坝的数值模拟分析可得到以下结论:

(1)带支撑钢构格栅坝各处位移随着钢球冲击速度的增加逐渐增大,基本呈现线性变化的规律,尤其在冲击作用点处结构的位移变化率最大,且距冲击作用位置越远位移变化率越小；

(2)结构各处应力值随着冲击速度的增加而增大,且距冲击作用位置较远的单元应力变化接近线性增长规律；

(3)随着冲击速度的提升,结构各柱脚支反力逐渐增大；

(4)结构加速度随冲击速度的变化规律并不明显。

[1]谢洪.泥石流灾害及防治[J].科学,2006,58(5):28-31.

[2]陈洪凯.公路泥石流研究及治理[M].北京:人民交通出版社,2004.

[3]崔鹏.我国泥石流防治进展[J].中国水土保持科学,2009,7(5):7-13.

[4]李德基.透水型拦挡坝在泥石流防治中的应用[J].中国地质灾害与防治学报,1997,8(4):60-66.

[5]代素云.透水型谷坊坝拦截泥石流形态数学模拟[J].水土保持应用技术,2010,30(2):7-9.

[6]中国地质调查局.DZ/T0239-2004 泥石流灾害防治工程设计规范[S].北京:中国标准出版社,2010.

[7]邓虎,陈宁生,胡桂胜,等.甘肃舟曲三眼峪沟泥石流动力学特征参数计算[J].重庆交通大学学报:自然科学版,2011,30(4):833-838.

[8]胡向德,王根龙,赵成,等.舟曲“8.8”三眼峪特大泥石流特征值分析[J].西北地质,2011,44(3):44-52.

The Influence of Impact Speed on Shock Resistance of Steel Grilled Dam with Support

Liu Xudong1,Hu Zhiming2

(1.School of Civil Engineering,Lanzhou University of Technology,Lanzhou 730050,China;2.Gansu Vocational Technical College of Construction,Lanzhou 730050,China)

The steel grilled dam with support plays an important role in holding up ratchel and reducing debris flow impact damage.This paper takes the supporting steel grille dam structure as model and uses nonlinear finite element software ANSYS / LS-DYNA to make numerical simulation.It uses the steel ball to stimulate the rock,taking different impact speed to apply impact loading in the trusses top beam-column joints of the grilled dam,and makes analysis of the structure's dynamic response under the effect of impact load.The results show that: the displacement of steel grilled dam with support increases with the increase of steel ball's impact speed,showing the law of linear variation.In particular,the displacement changing rate is the largest in the impact point.And the farther from the impact position,the smaller of the displacement changing rate.The stress value of the structure increases with the increase of impact speed,and the unit stress change that far form the impact position is close to the rule of linear growth; The pillar bearing reaction of the structure increases with enhancement of the impact speed.

Steel grilled dam with supports;Impact speed;Impact resistance;LS-DYNA;Numerical simulation

10.16468/j.cnki.issn1004-0366.2016.04.017.

2016-01-19;

2016-03-25.

刘旭东(1972-)，男，陕西宝鸡人,高级工程师,研究方向为建筑结构.E-mail:492967879@qq.com.

TV414

A

1004-0366(2016)04-0081-06

引用格式:Liu Xudong,Hu Zhiming.The Influence of Impact Speed on Shock Resistance of Steel Grilled Dam with Support[J].Journal of Gansu Sciences,2016,28(4):81-86.[刘旭东,胡志明.冲击速度对带支撑钢构格栅坝抗冲击性能的影响[J].甘肃科学学报,2016,28(4):81-86.]