毫米波雷达的多普勒扩展目标检测

康　猛

(南京电子技术研究所，　南京 210039)



·信号处理·

毫米波雷达的多普勒扩展目标检测

康猛

(南京电子技术研究所，南京 210039)

在毫米波雷达目标探测中，目标微动部件的微多普勒效应会引起目标回波频谱扩展，线性调频信号的时频耦合会导致目标距离扩展，从而使得目标难以检测。文中首先通过建模仿真，研究了目标回波的特点，然后结合实测数据分析了其复杂性，在此分析基础上提出了边沿检测、均值滤波质心检测、闭运算质心检测等检测方法，最后通过实测数据处理验证了各种方法的性能。

毫米波；扩展目标；均值滤波；闭运算

0　引　言

随着毫米波技术的不断发展，毫米波雷达在导弹制导、火控和跟踪、高分辨率成像以及敌我识别等诸多领域得到了广泛应用，世界主要发达国家也把毫米波技术作为军事电子技术的重点研究对象。

经典雷达目标检测理论基础假设目标为点目标[1]。随着雷达探测目标的类型逐渐复杂，特别是有些目标带有微动部件，使目标各散射点存在相对运动，在频谱上引起频谱展开，这种特征称为多普勒扩展，多普勒扩展范围与雷达波长成反比。由于毫米波雷达波长极小，因此目标的多普勒扩展非常明显。

本文通过建模研究了带微动部件目标的毫米波雷达回波，分析了多普勒扩展目标检测的难点，根据多普勒扩展目标特点提出了边沿检测、均值滤波质心检测、闭运算质心检测等检测方法。

1　目标回波模型

直升机的旋翼使直升机成为典型的多普勒扩展目标，以直升机为例，对多普勒扩展目标进行建模仿真，直升机的雷达回波主要由三部分组成：

1) 机身回波，雷达截面积(RCS)约几平方米。

2) 主旋翼回波，旋翼的转动会形成一定的频谱扩展。

3) 尾翼回波，类似于主旋翼，但叶片直径较小，由于受机身的遮挡，可以忽略。

因此，直升机回波可表示为机身回波与主旋翼回波的叠加

s0(t)=sp(t)+sb(t)+n(t)

(1)

式中：sp(t)为等效机身回波分量；sb(t)为桨叶调制回波；n(t)为噪声。

图1表示某一桨叶和雷达的几何关系，图中分别以雷达和桨叶旋转中心Q为坐标中心建立坐标系。方位角和仰角分别为α、β，桨叶旋转角速度为ωr，假设每个桨叶是同类线性刚性天线，且无桨叶遮挡，则根据图示的几何关系，t时刻的N个桨叶的合成回波可以表示为

(2)

图1　桨叶和雷达的几何关系图

其中，幅度函数为

(3)

相位函数为

(4)

式中：L1为桨叶起点和桨叶中心的距离；L2为桨叶终点和桨叶中心的距离；θ0为桨叶的旋转初相角。

对直升机基频回波进行仿真分析，参数为fr=200 kHz，λ=0.01 m，L1=0，L2=0.8 m，N=4，ωr=100 πrad/s，R0=5 000 m，h=500 m，α=0°，β=15°，目标回放频谱如图2所示，多普勒扩展范围为-45.8 kHz～+45.8 kHz。

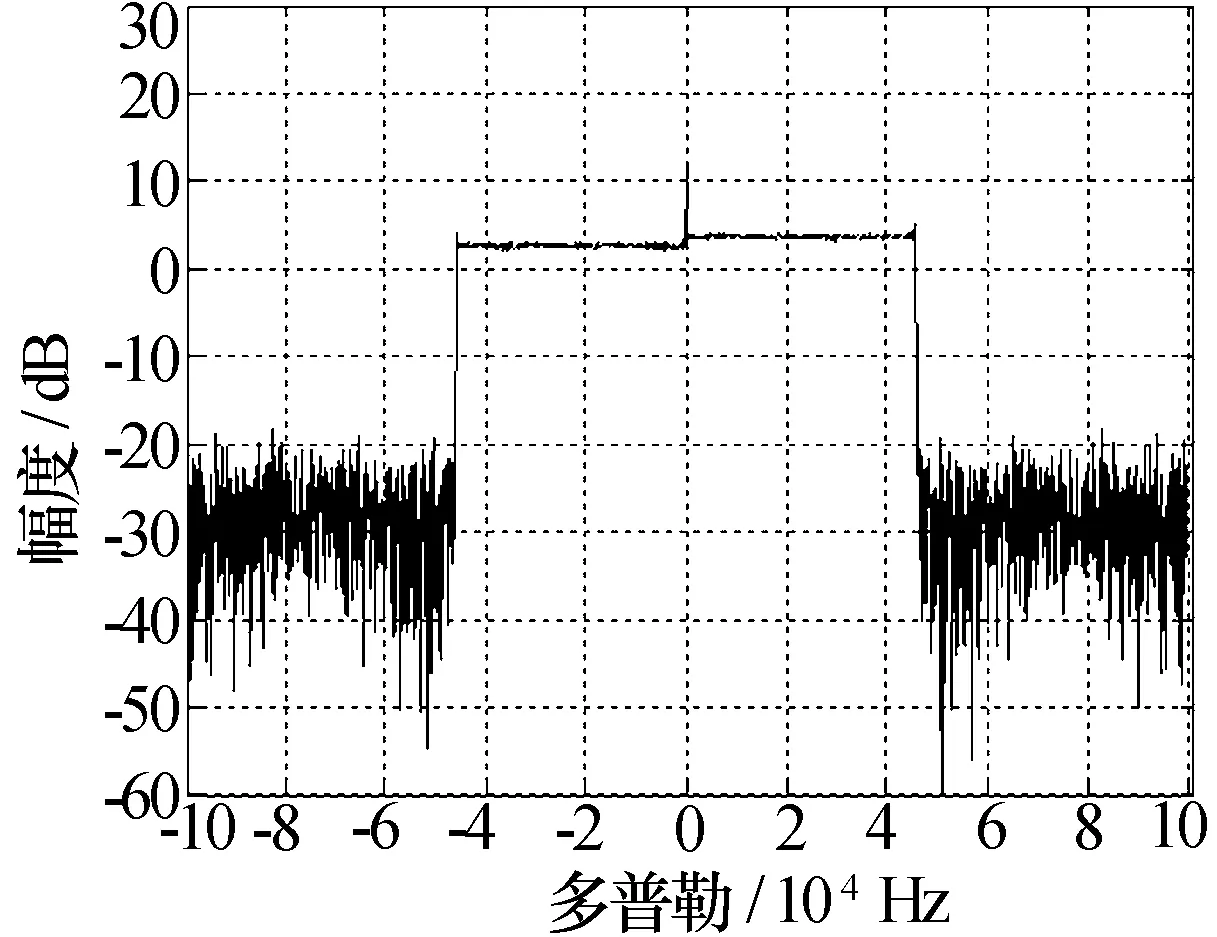
图2　直升机回波频谱

2　多普勒扩展对脉压影响

为了同时获得高的距离分辨率和探测距离，要求雷达信号具有大的时宽带宽积，考虑到多普勒容限性能，通常采用线性调频信号。线性调频回波信号为[1]

(5)

脉压结果为[1]

(6)

由式(6)可以得出，线性调频信号脉压(匹配滤波)对回波信号的多普勒频移不敏感，即使回波信号有较大的多普勒频移，脉压仍能起作用，但是会产生与多普勒成正比的附加时延。时延为

Δt=-fd/K=-fdT/B

(7)

雷达载频f0=30 GHz，信号带宽B=2 MHz，信号时宽T=1 ms，不同多普勒fd目标的脉压结果如图3所示，目标实际位置为209.9 km，当目标多普勒fd=40 kHz时，脉压时延对应着脉压峰值偏移3 km。

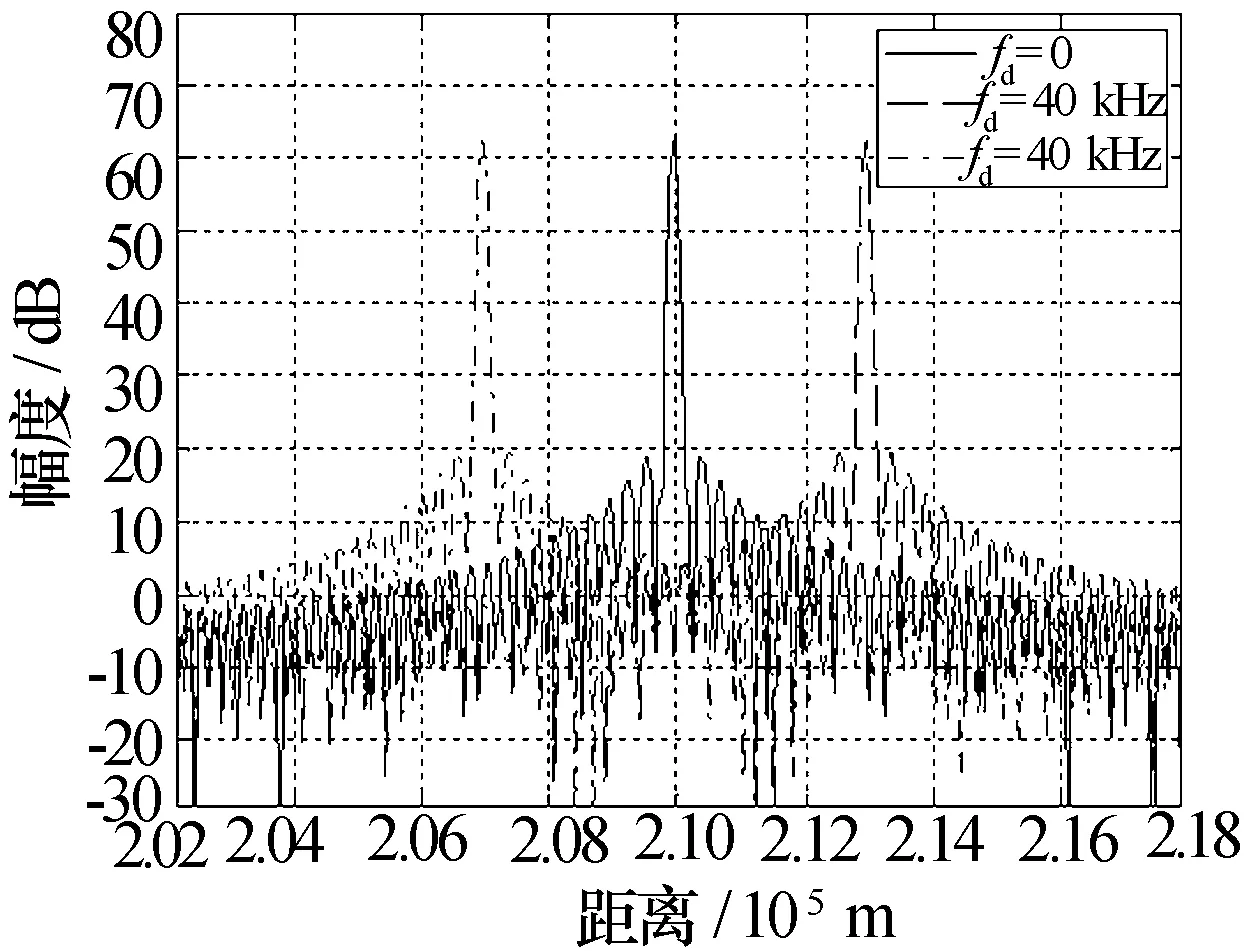
图3　不同多普勒目标脉压结果

根据式(2)，直升机的单个桨叶上每个散射点的径向速度不同，时延也不同。因此直升机回波脉压结果不是点目标，而是扩展目标。而且不同桨叶相对雷达的径向速度方向不同，对于整个直升机来说，有朝向雷达的微多普勒，有偏离雷达的微多普勒，如图4所示。脉压后距离既有正时延量，又有负时延量，因线性调频信号脉压的时频耦合作用，使目标在距离上也呈现为扩展目标，如图5所示。

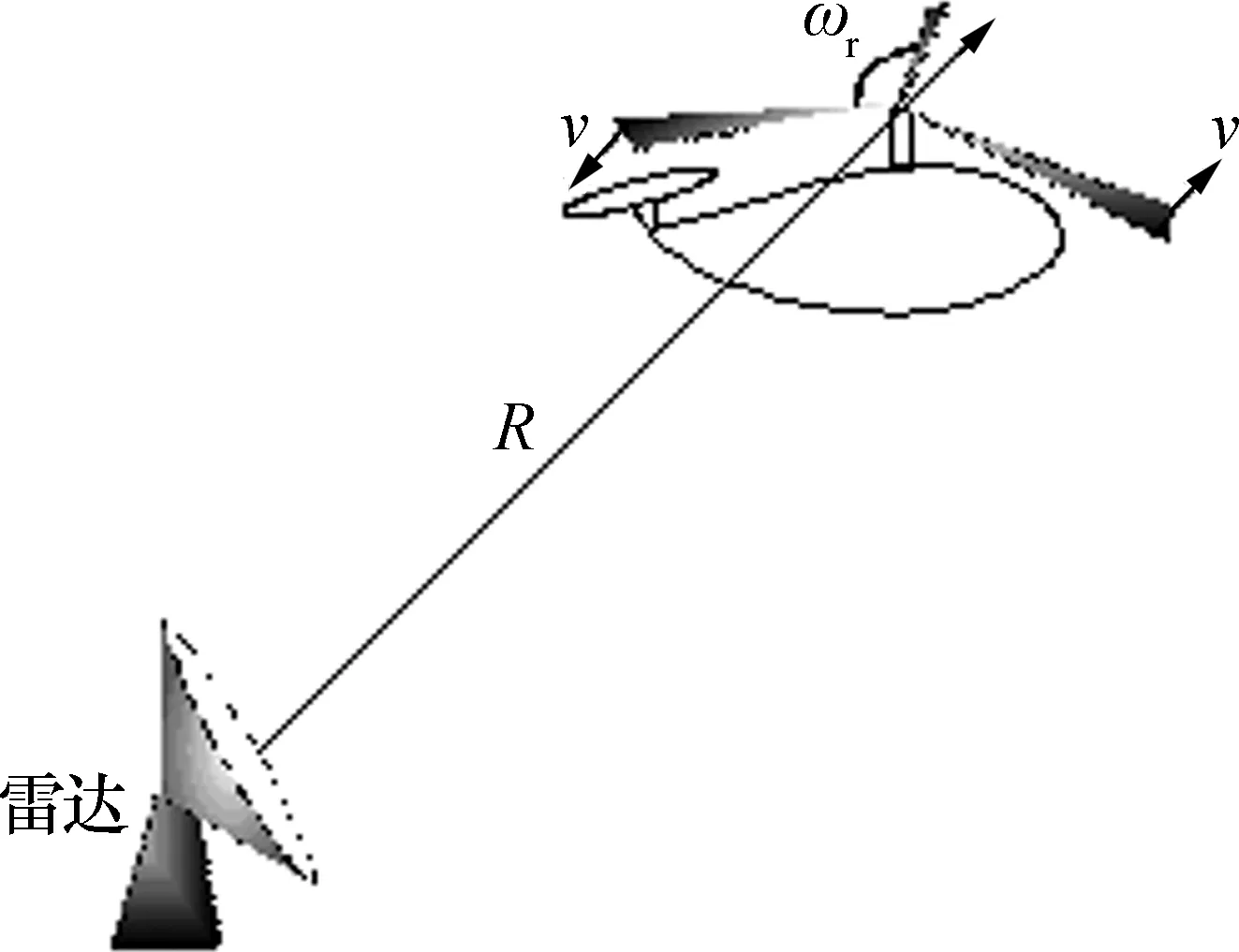
图4　微动方向示意图

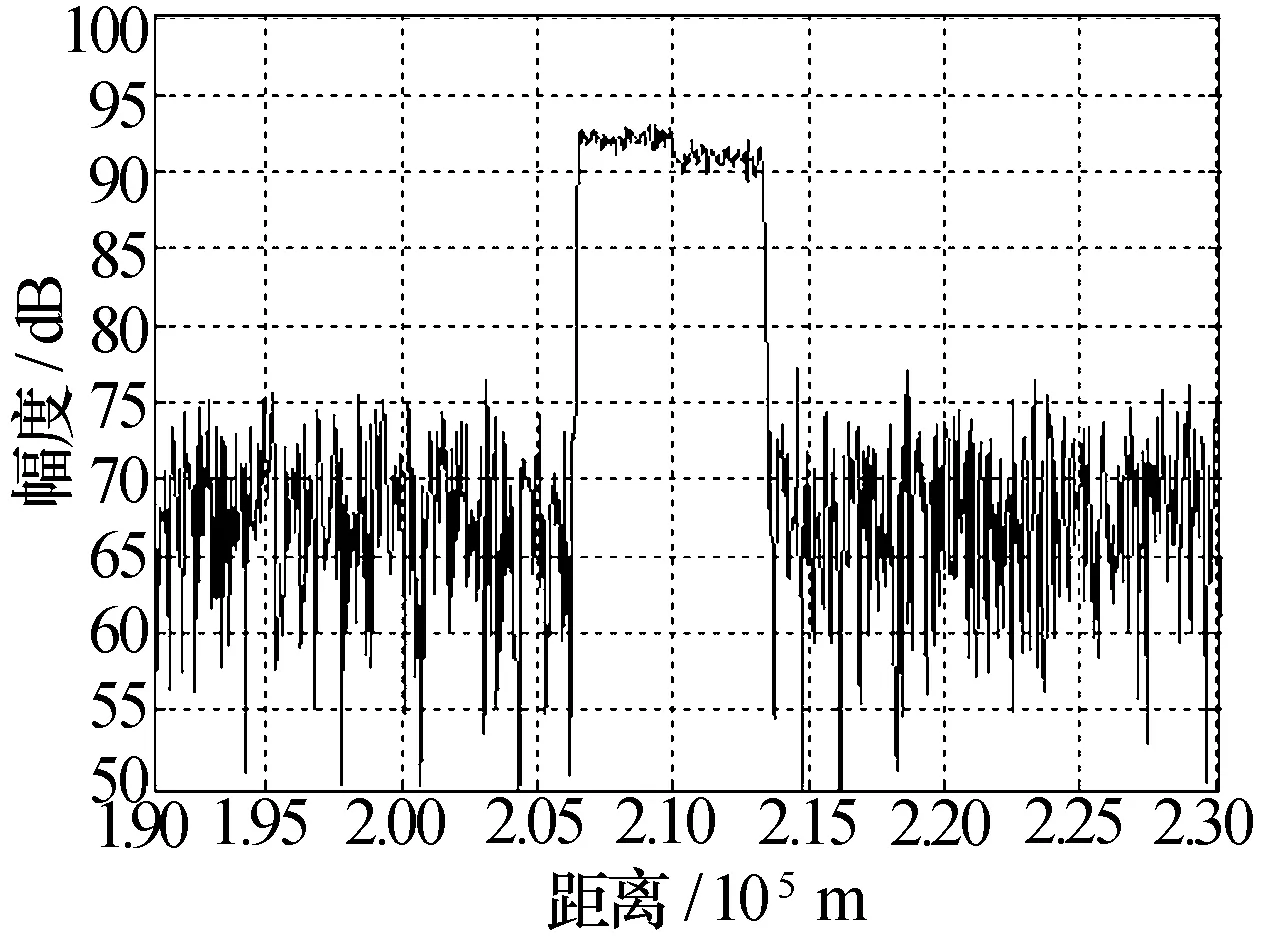
图5　脉压结果

3　目标多普勒扩展对检测的影响

目标部件旋转引起的多普勒扩展因脉冲的时频耦合作用使其在距离上也呈扩展。常规雷达目标检测时，认为目标为“点目标”或近似为“点目标”，若对扩展目标采用常规检查方法—单元平均选大恒虚警(GO-CFAR)会使目标漏检，检测方法失效[2-3]，仿真结果如图6所示。

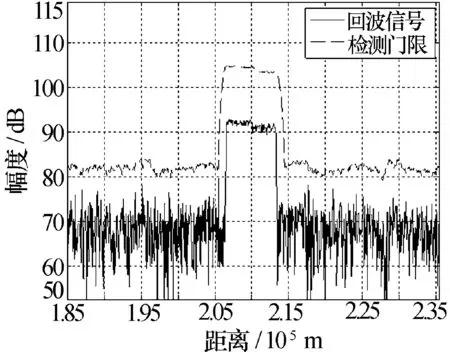
图6　单元平均选大CFAR

4　边沿检测

目标部件旋转方向有正负方向，从而引起的多普勒扩展含有正负方向分量，且呈对称性，因脉压的时频耦合作用引起目标距离上的扩展也呈对称性，如图5所示。

边沿检测方法是根据对称性的特点，可以先利用单元平均选小恒虚警(SO-CFAR)对目标的扩展边沿进行检测，再根据目标对称性，计算出目标位置，如图7所示，根据检测出的目标扩展边沿计算出目标真实位置。

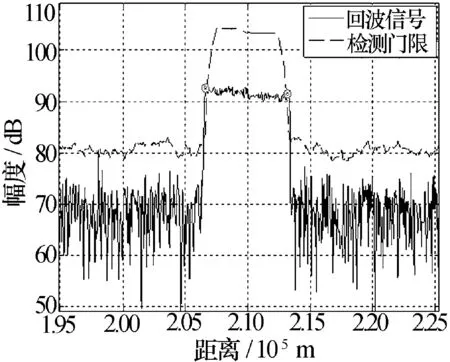
图7　边沿检测

然而，在实际中，目标微动部件情况十分复杂，存在如下情况，引起目标回波扩展十分不规则。

1)微动部件的散射点不是均匀分布；

2)微动部件受遮挡影响；

3)存在两个或多个微动部件。

例如，民航飞机有两个发动机，每个发动机又有多层涡扇，且受视角遮挡情况不同，因此其回波无法准确地建模仿真。图8示出了某民航飞机目标的回波信号及其边沿检测结果，可见若用边沿检测算法会把目标错误的分裂成多个目标。

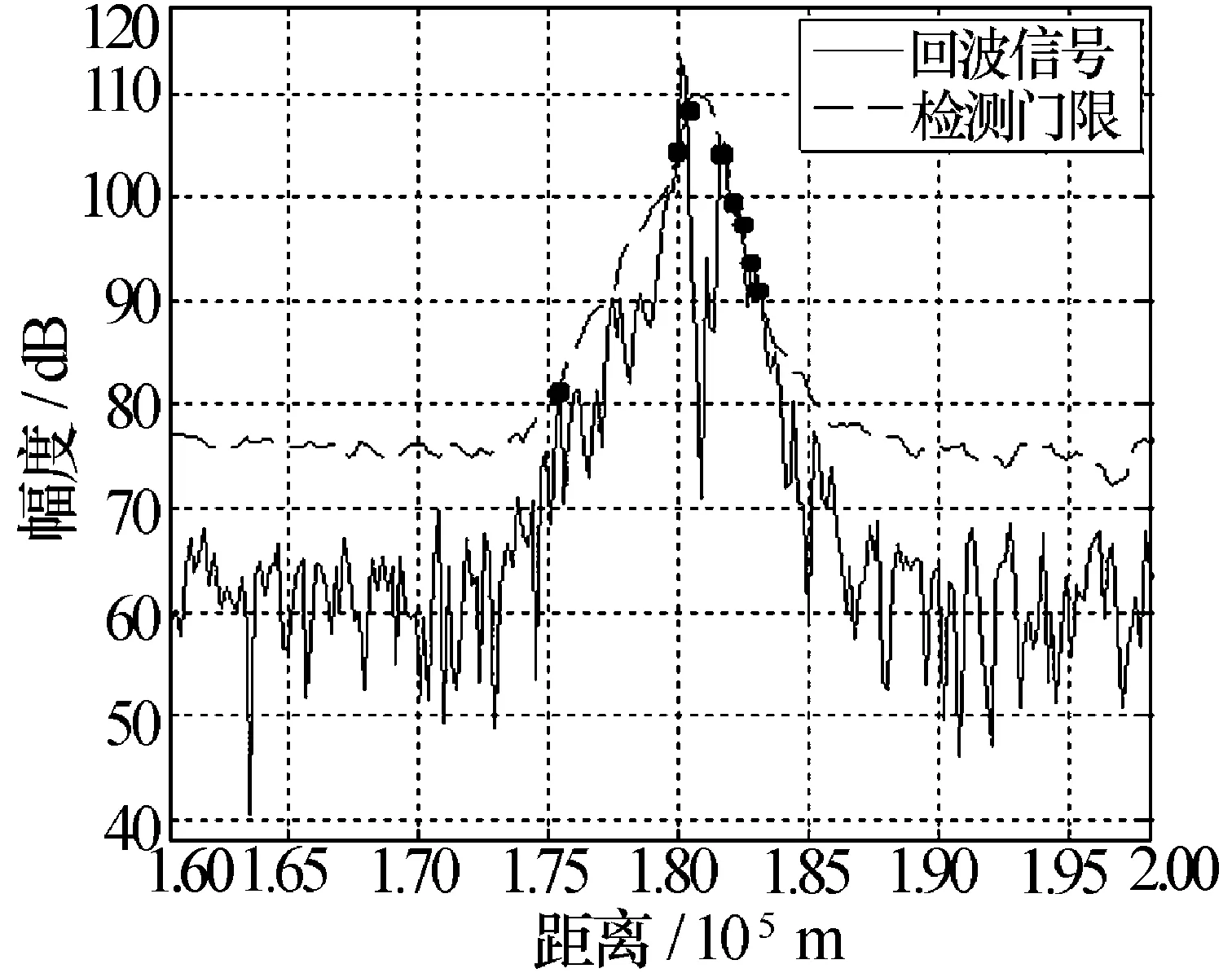
图8　民航目标回波及其边沿检测

针对民航回波的特点，在检测前希望平滑回波凹凸剧烈起伏，本文引入数字图像处理中的降噪技术—均值滤波，提出了均值滤波质心检测方法。

5　均值滤波质心检测

数字图像处理中有多种降噪平滑处理技术，本文结合最便于工程实现且十分有效的均值滤波处理，提出了均值滤波质心检测方法，具体处理步骤分三步：

1)均值滤波处理

均值滤波是数字图像处理中简单有效的降噪处理技术[4]，均值滤波通常采用一个含有奇数点的滑动窗口，用窗口中各点的均值代替中心点的值，对于一维数据处理，算法可以简化为

(8)

2)噪声恒虚警检测

利用噪声恒虚警处理，检测目标，并求出目标扩展范围，算法表达式如下

f(n)≥an*K

(9)

式中：an为噪声估值；K为检测门限。

3)求质心，提取目标位置

每个距离单元幅度作为该距离单元的质量，对连续过门限的距离单元求质心，质心作为目标位置，质心算法如下

(10)

式中：ntar为目标位置，[N1,N2]为目标扩展距离单元范围。

利用均值滤波质心检测算法对图8中的民航目标进行检测，结果如图9所示。根据目标GPS信息，质心作为目标位置是较准确的。

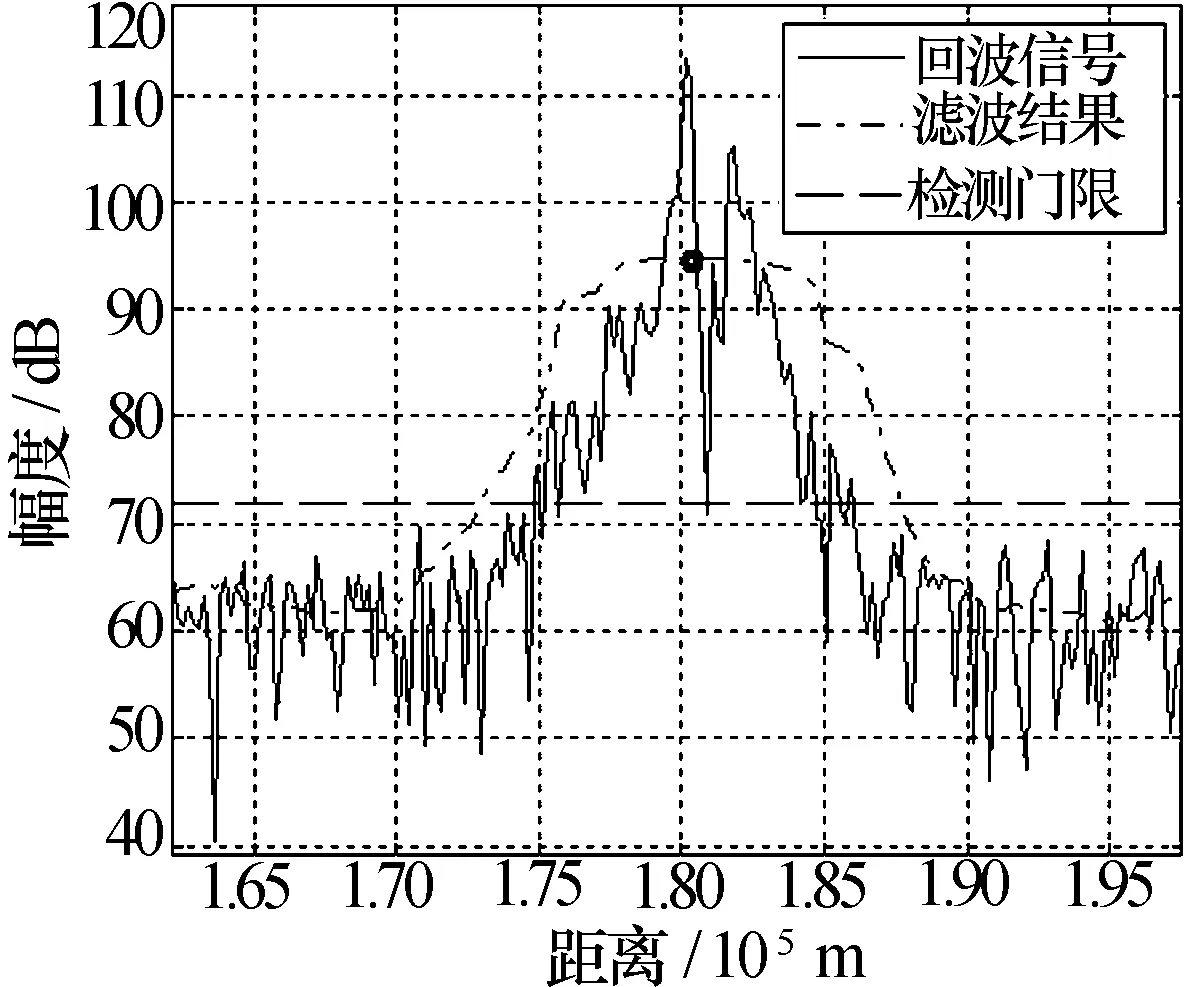
图9　民航目标回波及其均值滤波质心检测

雷达回波中可能存在多个目标，并且可能既有扩展目标又有非扩展目标，若简单地利用均值滤波质心检测会增加非扩展目标的检测损失。例如在某次试验中，雷达回波中存在两个扩展目标和一个非扩展目标，如图10所示，均值滤波质心检测虽然很好地检测出两个扩展目标但丢失了非扩展目标。

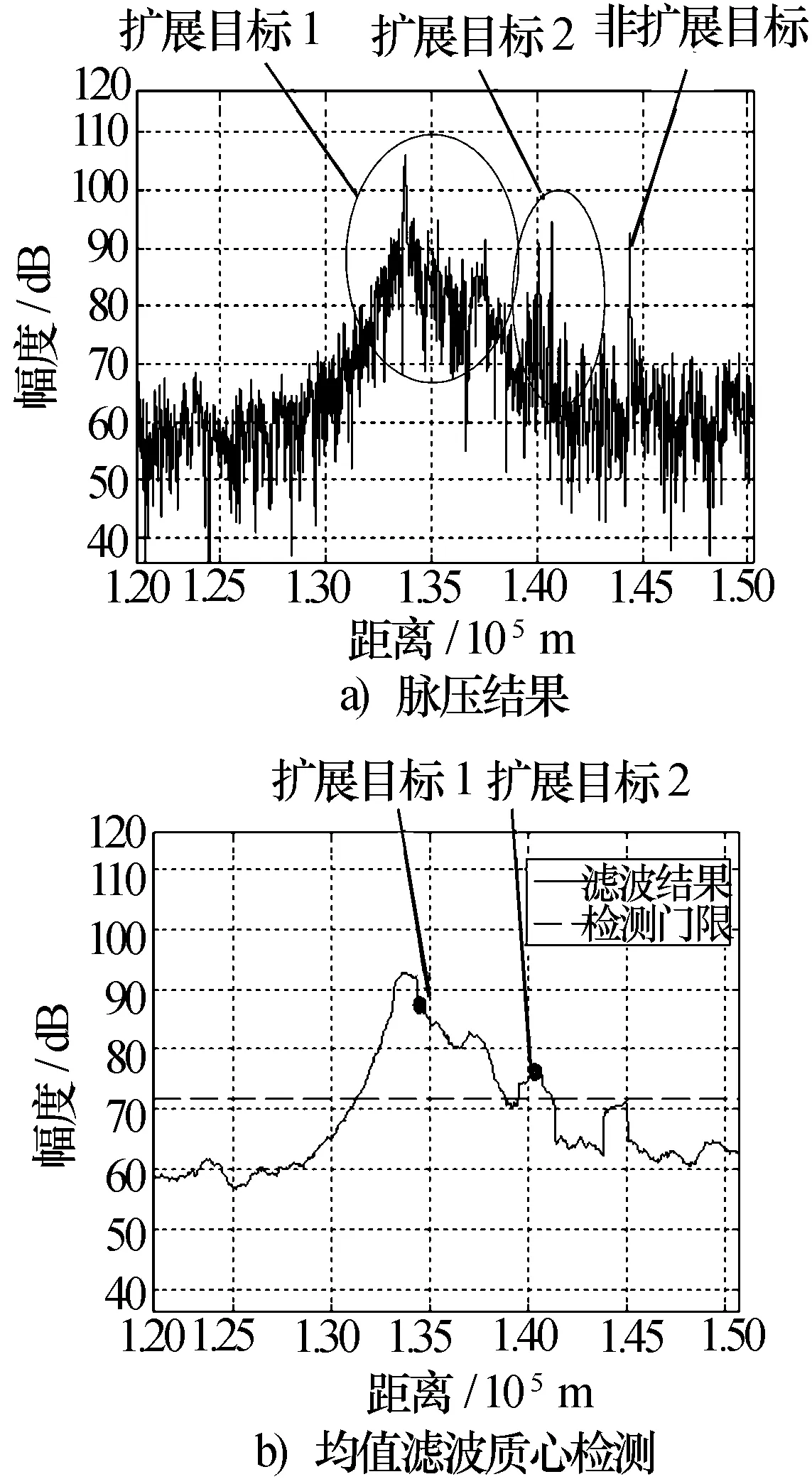
图10　复杂目标检测结果

因此，需要寻求一种既有能有效的检测扩展目标，又对非扩展目标有效的方法。为了实现此目标，需要一种算法只对扩展目标进行平滑，但对非扩展目标不平滑或少平滑。本文引入数字图像处理中闭运算，提出了闭运算质心检测方法。

6　闭运算质心检测

闭运算的几何解释，在边界外部转动球B，我们注意到方向向内的拐角变得圆滑了，而方向向外的拐角没有变化[4]，处理示意图如下，图11a)中B在A的外部边界上转动，图11b)的粗线表示闭运算的外部边界，图11c)完全的闭运算(阴影部分)。

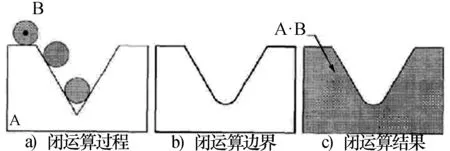
图11　闭运算示意图

针对雷达的一维数据，闭运算处理可简单解释为在数据边界上部转动B。闭运算一般会平滑狭窄的缺口，并保留尖刺，处理示意图如图12所示。

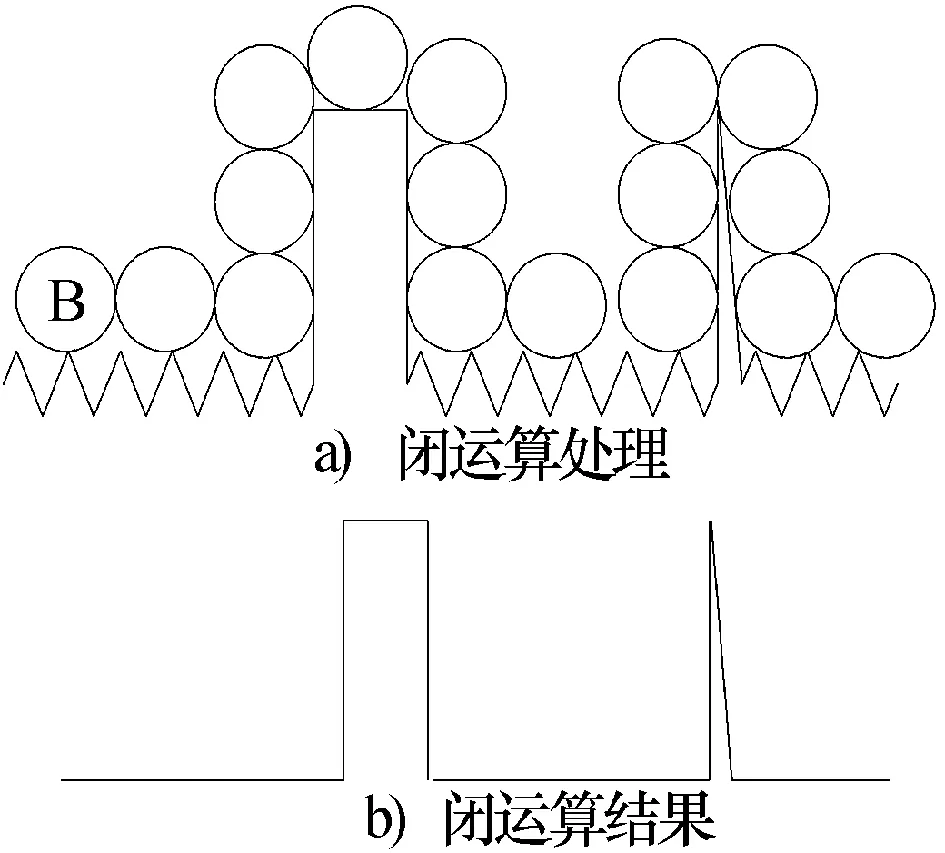
图12　一维数据的闭运算示意图

本文利用闭运算平滑缺口和保留尖刺的特点，提出闭运算质心检测方法。处理步骤分三步：

1)一维闭运算处理。对目标回波的脉压结果进行一维闭运算处理。闭运算的算法和仿真程序在文献[4-7]中有详细介绍，这里不赘述。

2)噪声恒虚警检测。对闭运算处理结果进行噪声恒虚警检测。

3)求质心，提取目标位置。利用闭运算质心检测方法对多复杂目标的检测结果如图13所示，扩展目标和非扩展目标都成功地检测出，并准确地提取出了目标位置信息。

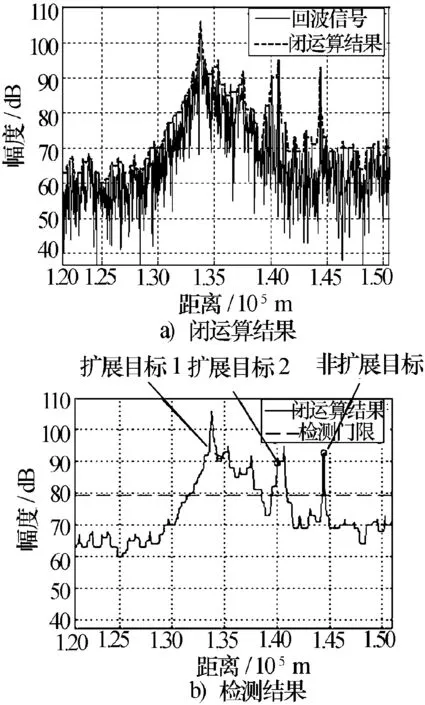
图13　闭运算质心检测

7　检测方法适用范围比较

本文针对多普勒扩展目标，先后提出了边沿检测、均值滤波质心检测、闭运算质心检测等三种方法，根据上述几节仿真和实测数据验证，各种检测方法的适用范围如表1所示。针对毫米波雷达，飞机目标普遍为扩展目标，均值滤波质心检测方法是一种简便有效的方法。

表1　各检测方法适用范围

8　结束语

本文详细研究了多普勒扩展目标的特点，分析了多普勒扩展对目标检测的影响。根据场景由简单到复杂，本文提出了边沿检测、均值滤波质心检测、闭运算质心检测方法，这些方法已在一种雷达中获得较好应用。

[1]林茂庸, 柯有安. 雷达信号理论[M]. 北京:国防工业出版社,1984.

LIN Maoyong, KE Youan. Radar signal theory[M]. Beijing: National Defense Industry Press, 1984.

[2]祝欢, 陈翼. 宽带信号检测方法与性能分析[J]. 现代雷达, 2015,37(9): 33-36.

ZHU Huan,CHEN Yi. New methods on wideband signal detection and performance analysis[J]. Modern Radar, 2015,37(9): 33-36.

[3]王晓红, 金林, 高俊姣. 频率步进雷达距离扩展目标检测算法研究[J]. 现代雷达, 2009, 31(5): 45-49.

WANG Xiaohong, JIN Lin, GAO Junjiao. A study on detection algorithm for range-distributed targets in stepped-frequency radar[J]. Modern Radar, 2009, 31(5): 45-49.

[4]GONZALEZ R C, WOODS R E. 数字图像处理[M]. 2版. 北京: 电子工业出版社, 2008.

GONZALEZ R C, WOODS R E. Digital image processing[M].2 nd ed. Beijing: Publishing House of Electronics Industry, 2008.

[5]王慧琴. 数字图像处理[M]. 北京：北京邮电大学出版社, 2006.

WANG Huiqin. Digital image processing[M]. Beijing: Beijing University of Posts and Telecommunication Press, 2006.

[6]孙兆林. MATLAB 6.x图像处理[M]. 北京: 清华大学出版社, 2002.

SUN Zhaolin. Image processing using MATLAB 6.x[M]. Beijing:Tsinghua University Press, 2002.

[7]张德丰. MATLAB数字图像处理[M]. 北京: 机械工业出版社, 2009.

ZHANG Defeng. Digital image processing using MATLAB[M]. Beijing: China Machine Press, 2009.

康猛男，1978年生，硕士，高级工程师。研究方向为雷达信号处理。

Spread-Doppler Target Detection of Millimeter Wave Radar

KANG Meng

(Nanjing Research Institute of Electronics Technology,Nanjing 210039, China)

For the target detection of millimeter wave radar the micro-Doppler effect induced by the micro-rotation parts of target spreads the spectrum of target echo, and the time-frequency coupling of the linear-frequency modulated signal extends the target in range, therefore the target is difficult to detect. In this paper, the features of target echoes are firstly investigated by modeling and simulation, then the complexity of measured data is analyzed. On the above basis of investigation, the edge-detection, mean-filter-centroid-detection, and close-operation-centroid-detection are presented and demonstrated using hte measured data.

millimeter wave radar; spread target; mean filter; close operation

康猛Email：13951939825@163.com

2016-03-11

2016-05-24

TN957.51

A

1004-7859(2016)07-0021-04

DOI：10.16592/ j.cnki.1004-7859.2016.07.006